Similar presentations:
Многогранники. Круглые тела
1.
22 сентябряКлассная работа.
2.
МНОГОГРАННИКИМногогранником называется тело, поверхность которого состоит из
конечного числа многоугольников, называемых гранями многогранника.
Стороны и вершины этих многоугольников называются соответственно
ребрами и вершинами многогранника.
Отрезки, соединяющие вершины многогранника, не принадлежащие одной
грани, называются диагоналями многогранника.
Многогранник называется выпуклым, если вместе с любыми двумя своими
точками он содержит и соединяющий их отрезок.
На рисунках приведены примеры выпуклых и невыпуклых многогранников
3.
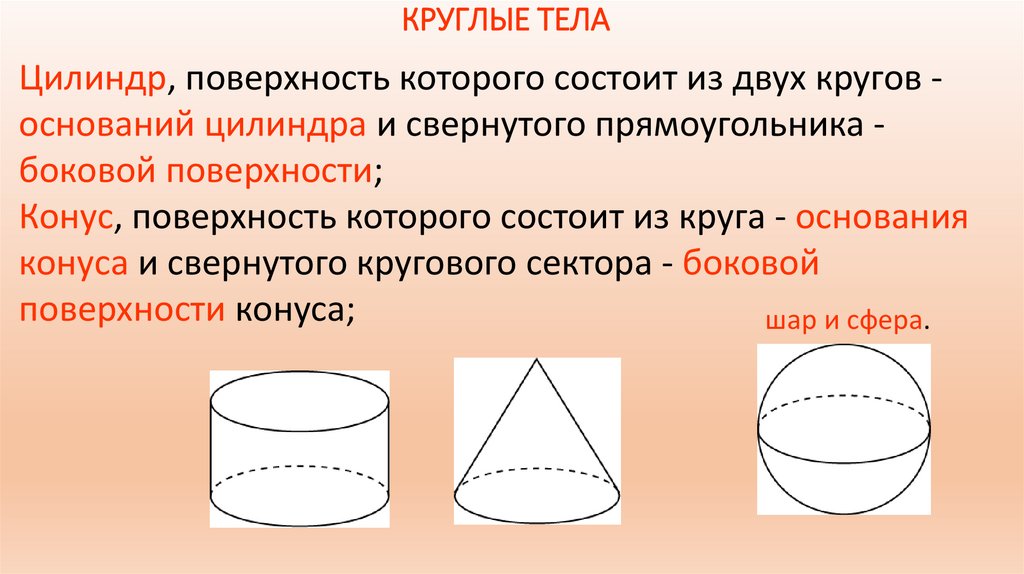
КРУГЛЫЕ ТЕЛАЦилиндр, поверхность которого состоит из двух кругов оснований цилиндра и свернутого прямоугольника боковой поверхности;
Конус, поверхность которого состоит из круга - основания
конуса и свернутого кругового сектора - боковой
поверхности конуса;
шар и сфера.
4.
КУБКубом называется многогранник, поверхность которого состоит из
шести квадратов.
Обычно куб изображается так, как показано на рисунке. А именно,
рисуется квадрат ABB1A1, изображающий одну из граней куба, и
равный ему квадрат DCC1D1, стороны которого параллельны
соответствующим сторонам квадрата ABB1A1. Соответствующие
вершины этих квадратов соединяются отрезками. Отрезки,
изображающие невидимые ребра куба, проводятся пунктиром.
5.
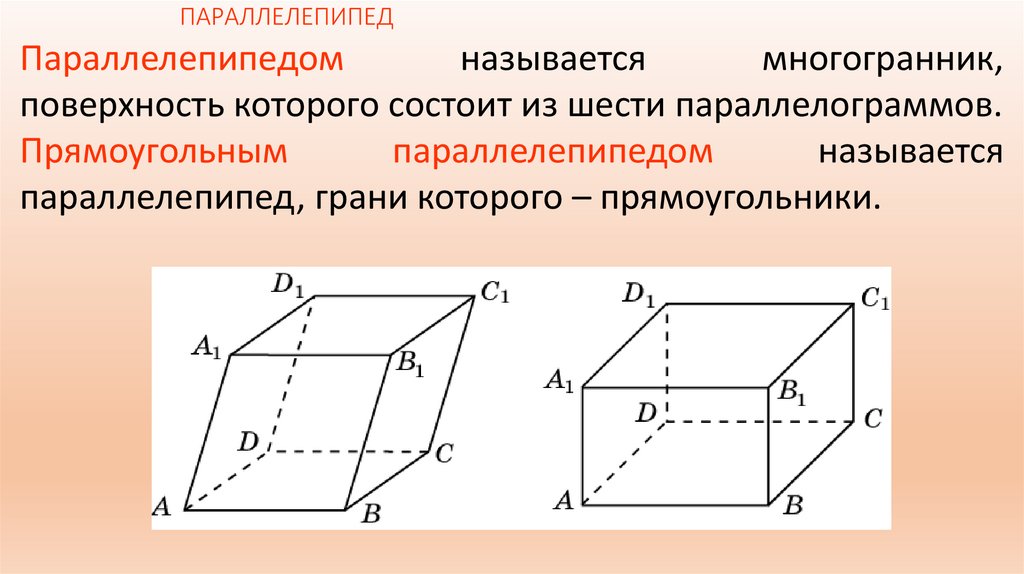
ПАРАЛЛЕЛЕПИПЕДПараллелепипедом
называется
многогранник,
поверхность которого состоит из шести параллелограммов.
Прямоугольным
параллелепипедом
называется
параллелепипед, грани которого – прямоугольники.
6.
ПАРАЛЛЕЛЕПИПЕДОбычно параллелепипед изображается так, как показано на
рисунке. А именно, рисуется параллелограмм ABB1A1,
изображающий одну из граней параллелепипеда, и равный ему
параллелограмм DCC1D1, стороны которого параллельны
соответствующим
сторонам
параллелограмма
ABB1A1.
Соответствующие вершины этих параллелограммов соединяются
отрезками. Отрезки, изображающие невидимые ребра куба,
проводятся пунктиром. В случае прямоугольного параллелепипеда
вместо параллелограммов, изображающих две грани, рисуются
равные прямоугольники.
7.
ПРИЗМАПризмой называется многогранник, поверхность которого состоит из двух
равных многоугольников, называемых основаниями призмы, и
параллелограммов, имеющих общие стороны с каждым из оснований и
называемых боковыми гранями призмы. Стороны боковых граней
называются боковыми ребрами призмы.
Призма называется n-угольной, если ее основаниями являются nугольники.
8.
ПРИЗМАНа рисунке изображена четырехугольная призма. ABCD и
A1B1C1D1 – равные четырехугольники с соответственно
параллельными сторонами. Соответствующие вершины этих
четырехугольников соединены отрезками. Отрезки,
изображающие невидимые ребра призмы, проводятся
пунктиром.
9.
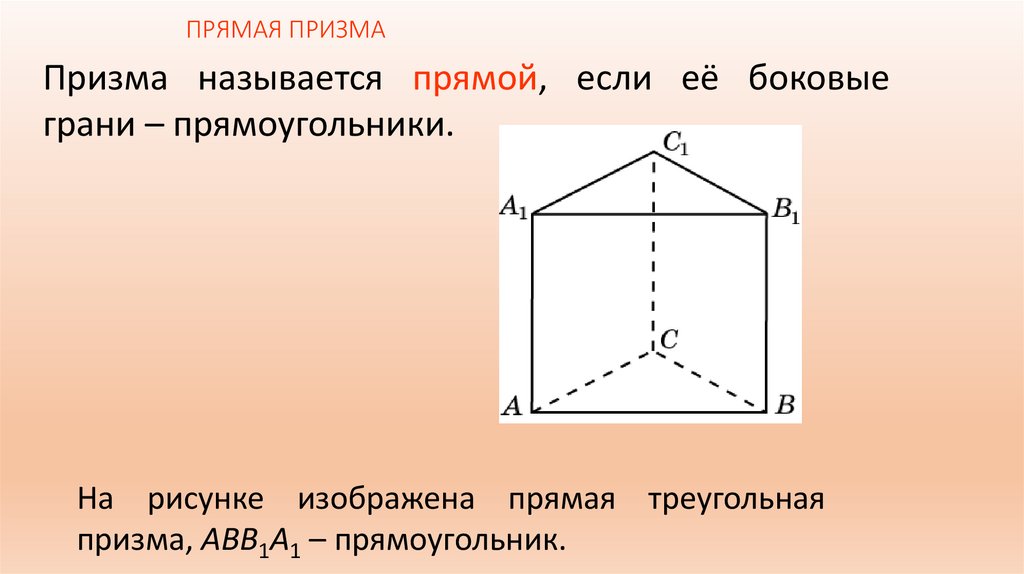
ПРЯМАЯ ПРИЗМАПризма называется прямой, если её боковые
грани – прямоугольники.
На рисунке изображена прямая треугольная
призма, ABB1A1 – прямоугольник.
10.
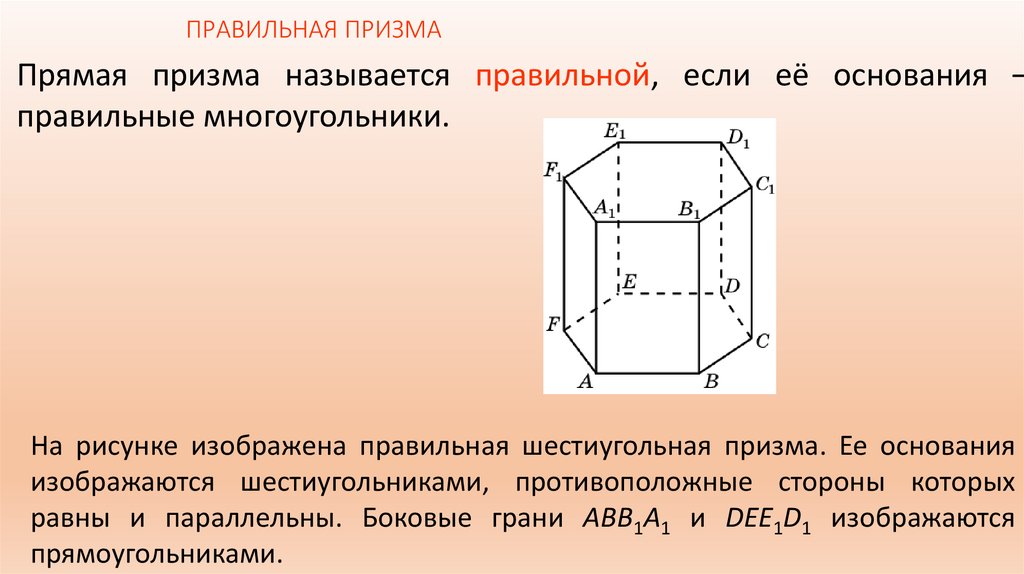
ПРАВИЛЬНАЯ ПРИЗМАПрямая призма называется правильной, если её основания –
правильные многоугольники.
На рисунке изображена правильная шестиугольная призма. Ее основания
изображаются шестиугольниками, противоположные стороны которых
равны и параллельны. Боковые грани ABB1A1 и DEE1D1 изображаются
прямоугольниками.
11.
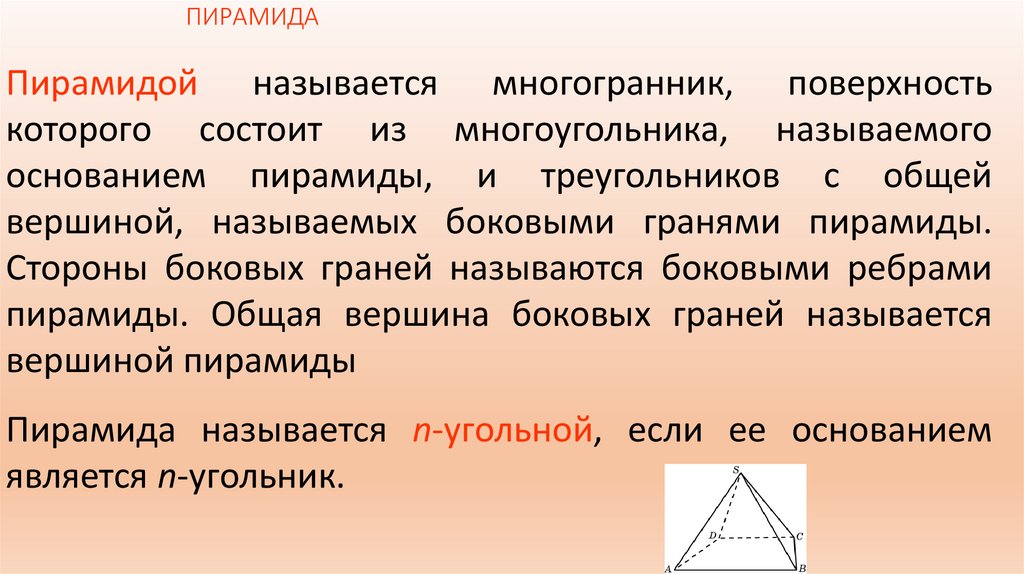
ПИРАМИДАПирамидой называется многогранник, поверхность
которого состоит из многоугольника, называемого
основанием пирамиды, и треугольников с общей
вершиной, называемых боковыми гранями пирамиды.
Стороны боковых граней называются боковыми ребрами
пирамиды. Общая вершина боковых граней называется
вершиной пирамиды
Пирамида называется n-угольной, если ее основанием
является n-угольник.
12.
ПРАВИЛЬНАЯ ПИРАМИДАПирамида называется правильной, если её основание –
правильный многоугольник и все боковые ребра равны.
На рисунках изображены правильная четырехугольная и правильная
шестиугольная пирамиды. Их основания изображаются соответственно
параллелограммом и шестиугольником, противоположные стороны которого
равны и параллельны.
13.
Многогранники 4Существуют ли многогранники, отличные от куба, все грани
которых – квадраты?
Ответ: Да, например, пространственный крест.
14.
1.СЕЧЕНИЕ.
14
15.
Разрежем тетраэдр на какие-нибудь две части.Многоугольник, полученный на
срезе, называют сечением
тетраэдра
16.
Таким образом можно получить сечениелюбого многогранника.
17.
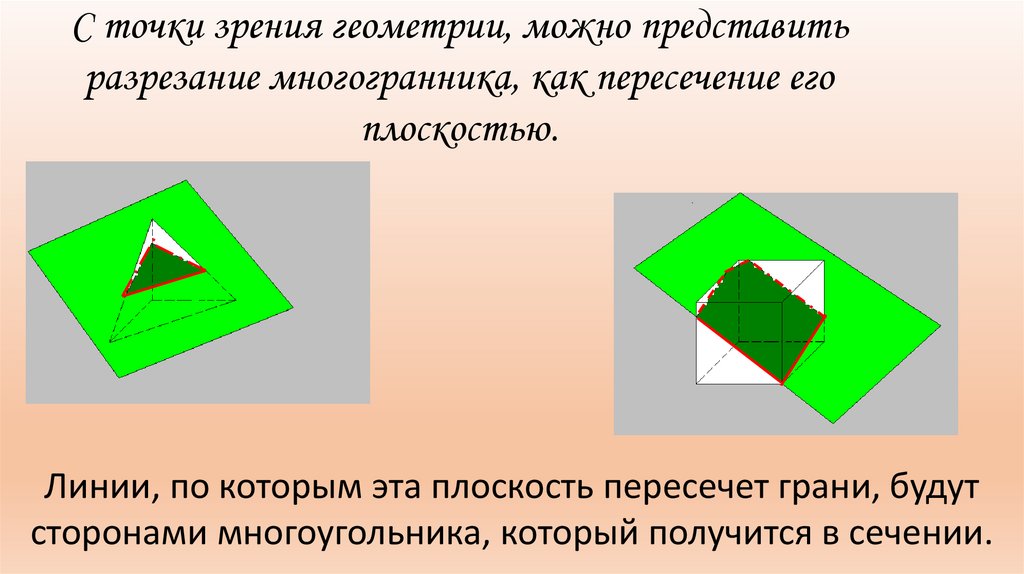
С точки зрения геометрии, можно представитьразрезание многогранника, как пересечение его
плоскостью.
Линии, по которым эта плоскость пересечет грани, будут
сторонами многоугольника, который получится в сечении.
18.
ОПРЕДЕЛЕНИЕСечением поверхности геометрических
тел плоскостью называется плоская
фигура,
полученная
в
результате
пересечения
тела
плоскостью
и
содержащая точки, принадлежащие как
поверхности тела, так и секущей
плоскости.
19.
Секущей плоскостью многогранника называется любаяплоскость, по обе стороны от которой имеются точки
А
данного многогранника.
N
M
α
K
D
В
С
20.
Секущая плоскость пересекает гранимногогранника по отрезкам.
Многоугольник, сторонами которого
являются эти отрезки, называется
сечением многогранника.
21.
2.«Особенности»
сечений.
21
22.
Особенность 1. Все стороны многоугольника-сечения лежатв плоскостях граней многогранника.
!
Никакая из сторон сечения не может проходить
внутри многогранника
Отрезок АС проходит внутри многогранника, поэтому треугольник
АВС (четырехугольник АСВМ) не является его сечением.
23.
Особенность 2. (Следует из аксиомы о пересечение двухплоскостей)
Каждую грань многогранника сечение может
пересекать не более, чем по одной прямой.
или
Ни одну из граней многогранника сечение не может
пересекать по двум (трем и т.д.) прямым.
АВСМК не является сечением параллелепипеда,
т.к. две его стороны, АВ и ВС, лежат на передней
грани, а, как известно, все общие точки двух
плоскостей лежат на единственной прямой –
прямой их пересечения.
24.
АВСМК не являетсясечением октаэдра, т.к.
две его стороны ВС и
МК лежат на одной его
грани.
!
Каждая грань многогранника содержит не
более одной стороны сечения.
25.
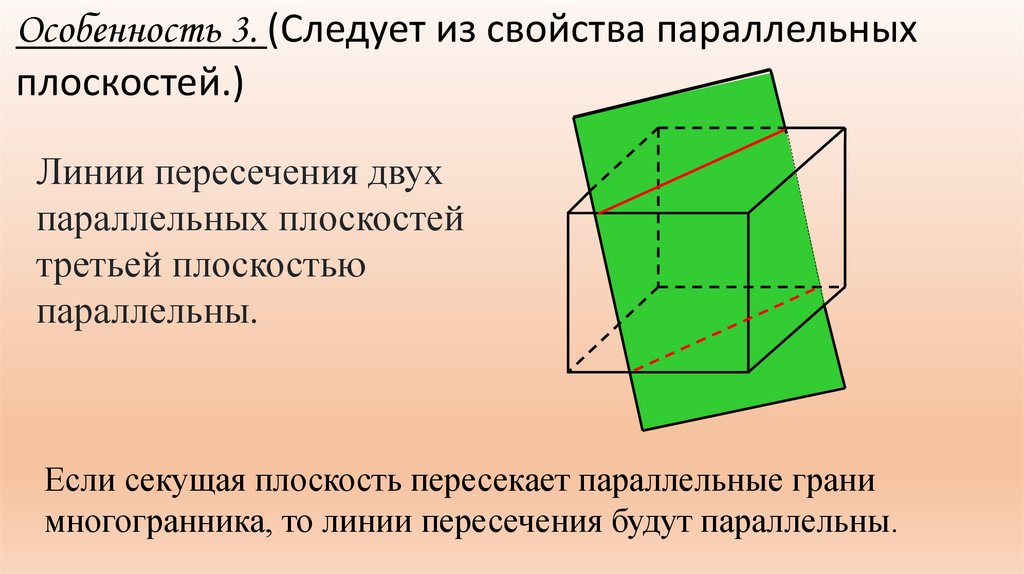
Особенность 3. (Следует из свойства параллельныхплоскостей.)
Линии пересечения двух
параллельных плоскостей
третьей плоскостью
параллельны.
Если секущая плоскость пересекает параллельные грани
многогранника, то линии пересечения будут параллельны.
26.
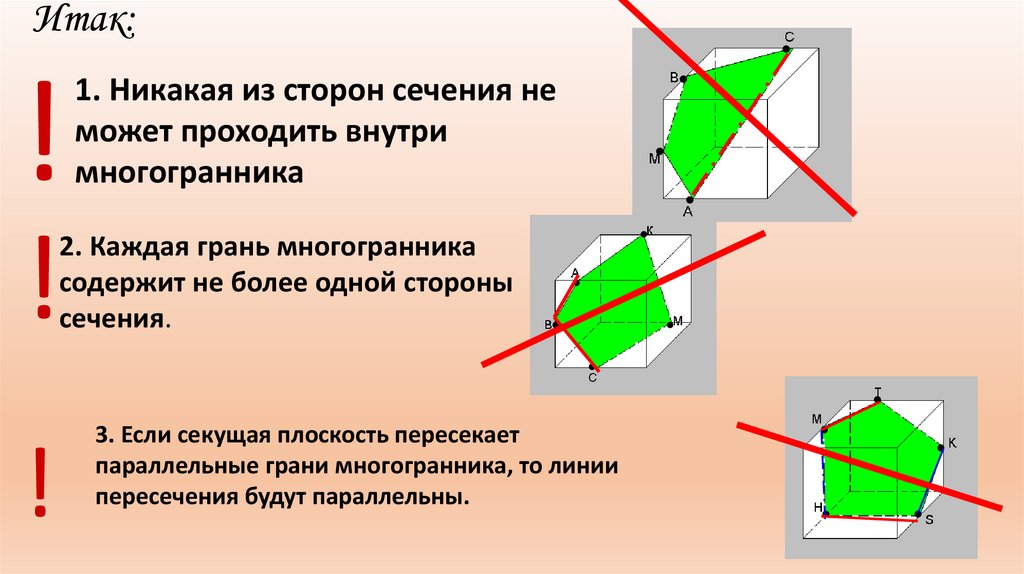
Итак:!
1. Никакая из сторон сечения не
может проходить внутри
многогранника
!
2. Каждая грань многогранника
содержит не более одной стороны
сечения.
!
3. Если секущая плоскость пересекает
параллельные грани многогранника, то линии
пересечения будут параллельны.
27.
AAB ∩ m = C
M
B
C
C
m
B
A
N
D
MN ∩ BA = K
K
Рис. 1
Рис. 2
28.
Рис. 3Рис. 4
29.
3.Построение
сечений.
29
30.
Задачи напостроение
Часть первая – само
построение и описание
построения.
Часть вторая –
доказательство того, что
построенный
многоугольник и есть
искомое сечение.
31.
В условиях задач на построение сечений обычно указываетсянесколько точек, принадлежащих сечению и/или
дополнительные условия, которым должно соответствовать
построенное сечение.
Данные точки могут лежать на
и/или на его гранях
ребрах многогранника
D
M
M
N
N
A
K
C
K
B
N принадлежит (ADB)
32.
DN
M
K
A
B
C
33.
Если соединив данные в условии точки, мы получиммногоугольник, все стороны которого будут лежать на гранях
многогранника, то сечение построено.
1.M∈ (ADC) , N ∈ (ADC) => MN ( ADC )
D
M
2. M∈ (ADB), K∈(ADB) =>
N
A
C
MK ( ADB )
3. K ∈ (BDC), N ∈ (BDC) => KN (BDC )
K
B
(MNK) – искомое сечение.
Но это может произойти только тогда, когда каждые две
соединяемые нами точки лежат в одной грани.
34.
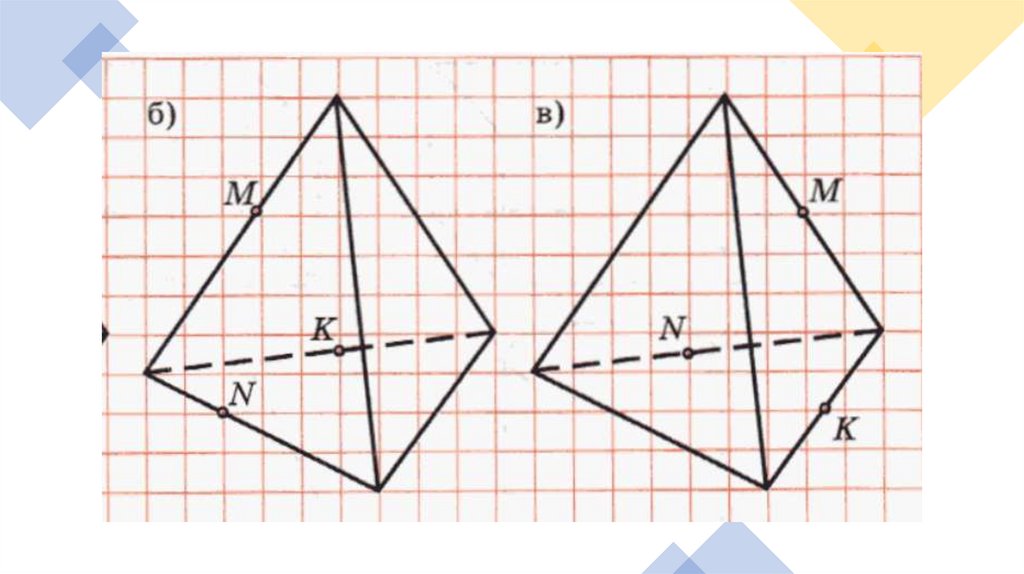
Задача №1: Постройте сечение тетраэдраплоскостью, проходящей через заданные точки
M,N,K.
M
K
N
35.
36.
37.
Построитьсечение,
проходящее
через точки
M, N, K
B1 N
C1
K
A1
M
A
D1
B
C
D
38.
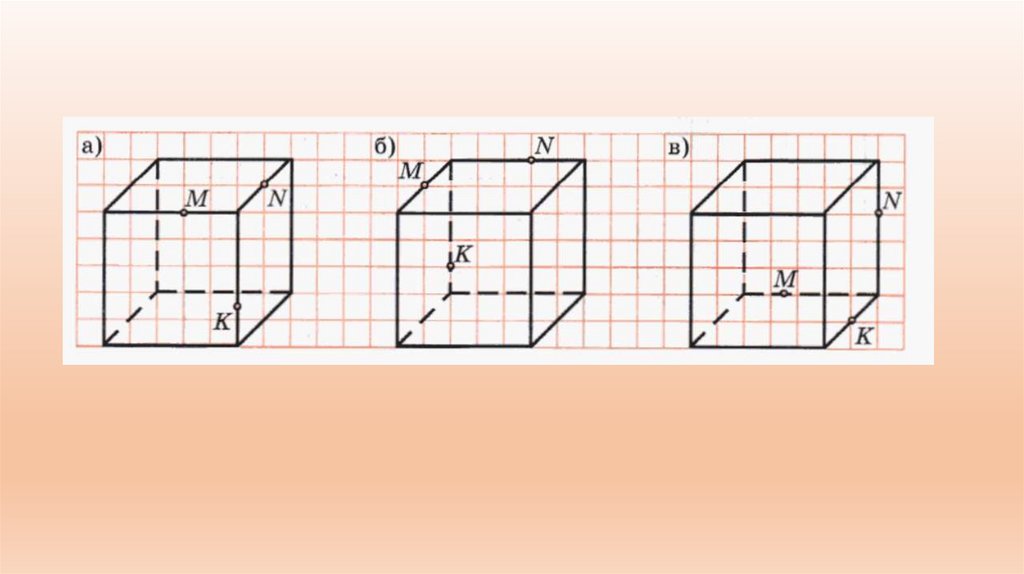
Если же какие-нибудь две точки не лежат в одной плоскости,то, соединив их, мы получим отрезок лежащий внутри
многогранника
Точки М и N не лежат в одной грани.
N
K
M
Следовательно, отрезок МN лежит
внутри параллелепипеда. Значит,
треугольник MNK не является
сечением.
(см. особенность сечений №2)
В таких случаях надо:
1) использовать все известные знания из теории;
2) Использовать дополнительные условия задачи;
3) Использовать специальные способы построения
сечений.
39.
Построить сечение, проходящее через точки M, N, KB
N
C
1
В этом случае мы должны
вспомнить, что
противоположные грани
параллелепипеда
параллельны.
Следовательно, секущая
плоскость пересечет их по
параллельным прямым
(особенность сечений
№3).
1
K
A1
M
A
D1
B
C
D
40.
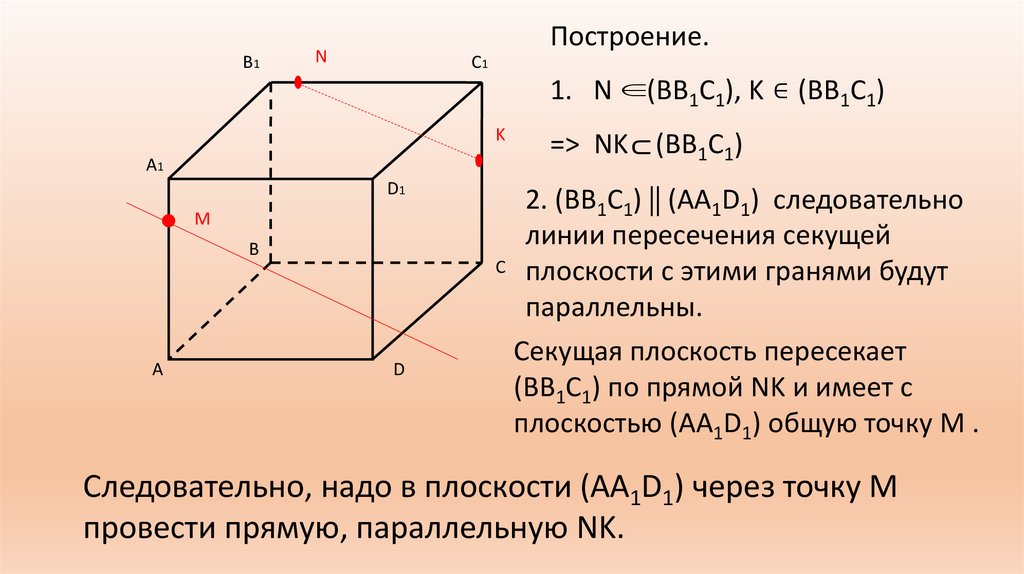
В1Построение.
N
С1
1. N (BB1C1), K ∈ (BB1C1)
K
А1
D1
M
В
А
D
=> NK ⊂ (BB1C1)
2. (BB1C1) || (AA1D1) следовательно
линии пересечения секущей
С плоскости с этими гранями будут
параллельны.
Секущая плоскость пересекает
(BB1C1) по прямой NK и имеет с
плоскостью (AA1D1) общую точку M .
Следовательно, надо в плоскости (AA1D1) через точку М
провести прямую, параллельную NK.
41.
Т.к. проведенная прямая и прямая DD1 лежат в одной плоскости, онипересекутся. Назовем точку пересечения – R.
3. Теперь в грани DD1C1С есть две
N
В1
С1
точки, принадлежащие плоскости
S
сечения: K и R. Соединим их.
K
4.Т.к. грани DD1C1 и AA1B1
параллельны и М AA1B1, то,
аналогично п.2,
M
D1
В
проведем в плоскости AA1B1 через
точку М прямую, параллельную KR.
С
R
А
D
Она пересечет прямую А1B1 в точке S (аналогично п.3).
42.
NВ1
С1
S
K
M
D1
В
С
R
А
D
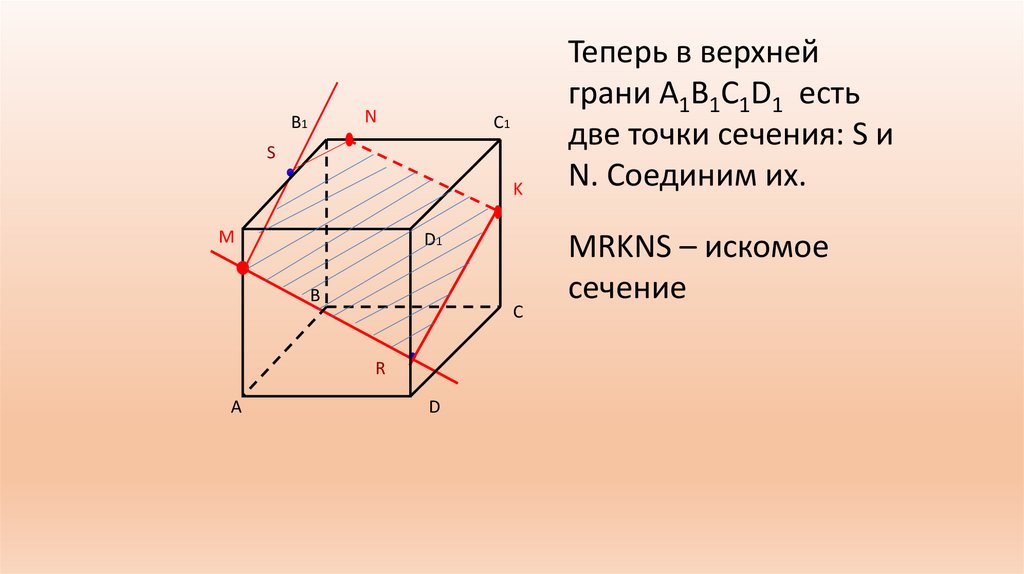
Теперь в верхней
грани A1B1C1D1 есть
две точки сечения: S и
N. Соединим их.
MRKNS – искомое
сечение

































 mathematics
mathematics








