Similar presentations:
Многогранники и тела с кривыми поверхностями
1. МНОГОГРАННИКИ И ТЕЛА С КРИВЫМИ ПОВЕРХНОСТЯМИ
Геометрические тела условно можно подразделить на двакласса: многогранники и тела с кривыми поверхностями.
Многогранник представляет собой тело, ограниченное со
всех сторон плоскими многоугольниками (гранями). Пересекаясь
друг с другом, грани образуют ребра, а те в свою очередь на
сходящихся концах – вершины.
Многогранник называется выпуклым, если он весь
расположен по одну сторону от плоскости каждой грани, и
правильным, если все его грани, плоские и многогранные углы
равны между собой.
Кривую поверхность можно представить как траекторию
движения некоторой линии (образующей) в пространстве.
Образующая может быть прямой или кривой линией. Если
поверхность образуется движением прямой, то она называется
линейчатой, если – кривой, то нелинейчатой. Примерами
простейших линейчатых поверхностей являются конус и цилиндр.
2. 1. Пирамида - это многогранник, одна грань которого - многоугольник, а остальные грани - треугольники с общей вершиной.
1. Пирамида - это многогранник, одна грань которого многоугольник, а остальные грани - треугольники с общейвершиной. Пирамида называется правильной, если в
основании лежит правильный многоугольник и высота
пирамиды проходит через центр многоугольника.
Пирамида называется усеченной, если вершина её
отсекается плоскостью
3. 2. Призма - многогранник, две грани которого (основания призмы) представляют собой равные многоугольники с взаимно
параллельными сторонами, а все другие гранипараллелограммы. Призма называется прямой, если её
ребра перпендикулярны плоскости основания. Если
основанием призмы является прямоугольник, призму
называют параллелепипедом
4. 3. Призматоид - многогранник, ограниченный двумя многоугольниками, расположенными в параллельных плоскостях (они являются его
основаниями); его боковыеграни представляют собой треугольники или трапеции,
вершины которых являются и вершинами многоугольников
оснований
5. 4. Тела Платона. Многогранник, все грани которого представляют собой правильные и равные многоугольники, называют
4. Тела Платона. Многогранник, все грани которого представляют собойправильные и равные многоугольники, называют правильными. Углы при
вершинах
такого
многогранника
равны
между
собой.
Существует пять типов правильных многогранников. Эти
многогранники и их свойства были описаны более двух тысяч лет назад
древнегреческим философом Платоном, чем и объясняется их общее
название.
Каждому правильному многограннику соответствует другой
правильный многогранник с числом граней, равным числу вершин данного
многогранника. Число ребер у обоих многогранников одинаково.
Тетраэдр - правильный четырехгранник. Он ограничен четырьмя
равносторонними треугольниками (это - правильная треугольная пирамида).
6. Гексаэдр - правильный шестигранник. Это куб, состоящий из шести равных квадратов.
Гексаэдр- правильный шестигранник.
состоящий из шести равных квадратов.
Это
куб,
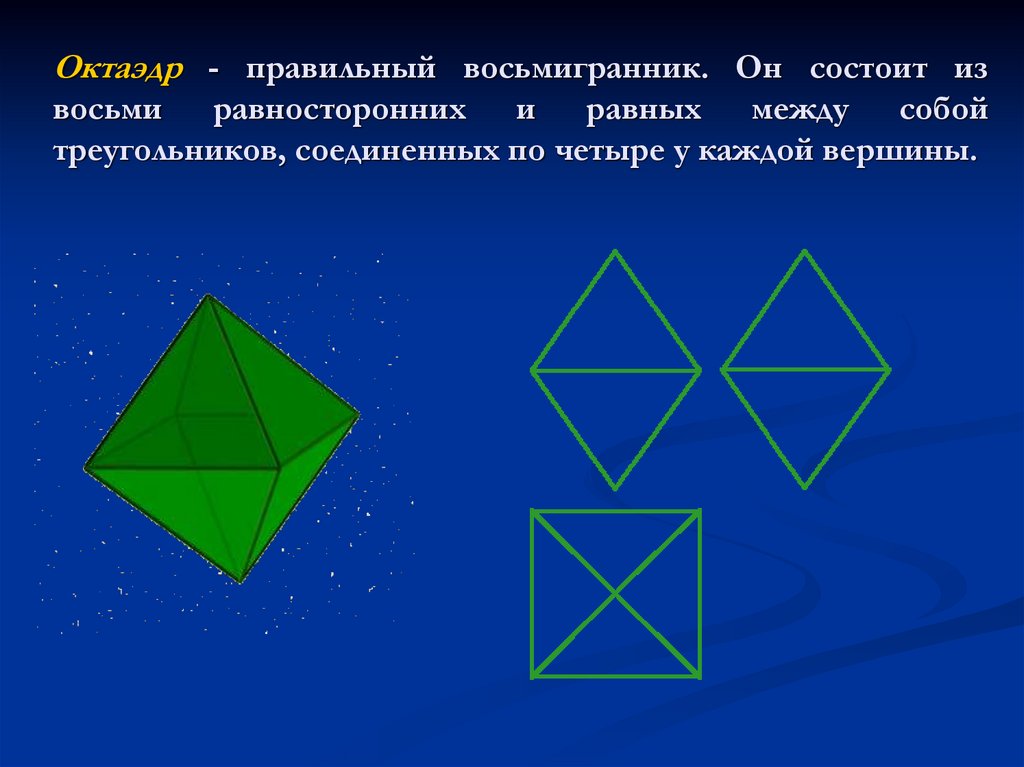
7. Октаэдр - правильный восьмигранник. Он состоит из восьми равносторонних и равных между собой треугольников, соединенных по
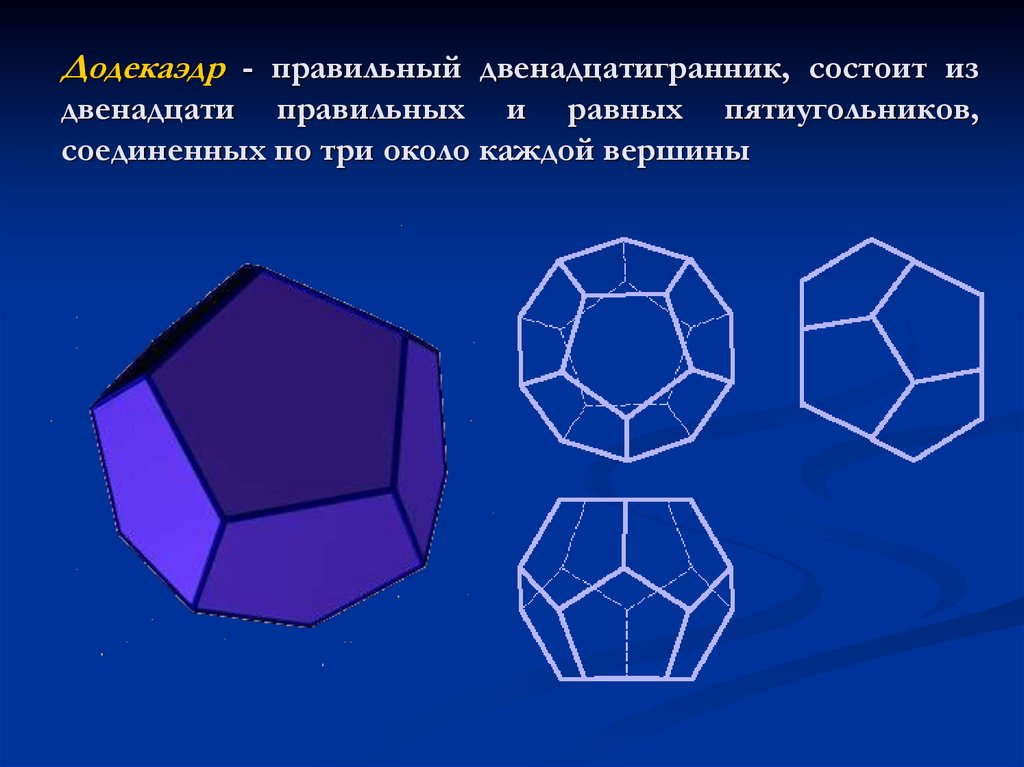
четыре у каждой вершины.8. Додекаэдр - правильный двенадцатигранник, состоит из двенадцати правильных и равных пятиугольников, соединенных по три около
каждой вершины9. Икосаэдр - состоит из 20 равносторонних и равных треугольников, соединенных по пять около каждой вершины
Икосаэдр - состоит из 20 равносторонних и равныхтреугольников,
вершины
соединенных
по
пять
около
каждой
10. 5. Звездчатые формы и соединения тел Платона. Кроме правильных выпуклых многогранников существуют и правильные
5. Звездчатые формы и соединения тел Платона. Кроме правильныхвыпуклых многогранников существуют и правильные выпукловогнутые
многогранники.
Их
называют
звездчатыми
(самопересекающимися). Рассматривая пересечения продолжения
граней Платоновых тел, мы будем получать звездчатые
многогранники.
Звездчатый октаэдр - восемь пересекающихся плоскостей граней
октаэдра отделяют от пространства новые "куски", внешние по
отношению к октаэдру. Это малые тетраэдры, основания которых
совпадают с гранями октаэдра. Его можно рассматривать как
соединение двух пересекающихся тетраэдров, центры которых
совпадают с центром исходного октаэдра. Все вершины звездчатого
октаэдра совпадают с вершинами некоторого куба, а ребра его
являются диагоналями граней (квадратов) этого куба. Дальнейшее
продление граней октаэдра не приводит к созданию нового
многогранника. Октаэдр имеет только одну звездчатую форму. Такой
звездчатый многогранник в 1619 году описал Кеплер (1571-1630) и
назвал его stella octangula - восьмиугольная звезда.
11.
12. ПЕРЕСЕЧЕНИЕ МНОГОГРАННИКА ПЛОСКОСТЬЮ
Сечение многогранника плоскостью представляет собойплоскую замкнутую ломаную линию.
Построение сечения можно провести двумя способами:
способом «граней» – найти линии пересечения граней с
заданной плоскостью;
способом «ребер» – найти точки встречи ребер пирамиды с
плоскостью и последовательно соединить их.
13. ПЕРЕСЕЧЕНИЕ МНОГОГРАННИКА ПЛОСКОСТЬЮ
f0f0
f0
S
f0
N3
N1
x
X
N2
N1 1
N2
3
2
A
A
C
B
N3
1
C
3
M1
S
2
h0
h0
B
h0
M2
h0
M3
14. ПЕРЕСЕЧЕНИЕ КОНУСА И ЦИЛИНДРА ПЛОСКОСТЬЮ
Для построения сечения конуса или цилиндра плоскостью в неенеобходимо вписать многогранник (соответственно пирамиду или призму),
построить сечение вписанного многогранника плоскостью, а затем полученные на
ребрах многогранника точки соединить плавной кривой линией по лекалу.
В результате получим приближенное решение задачи, точность которого
будет определяться числом граней вписанного многогранника.
15. ПЕРЕСЕЧЕНИЕ КОНУСА И ЦИЛИНДРА ПЛОСКОСТЬЮ
f0 f0f0
f0
B F O2 C E
D
A
N1
N2
4
x
C
B
5
1 N3 O1 2
3
N2
N1
N3
4
O2
A
O1
D 3
E
F
h0
5
M1 1
h0
2
M3
M2
h0
h0
X
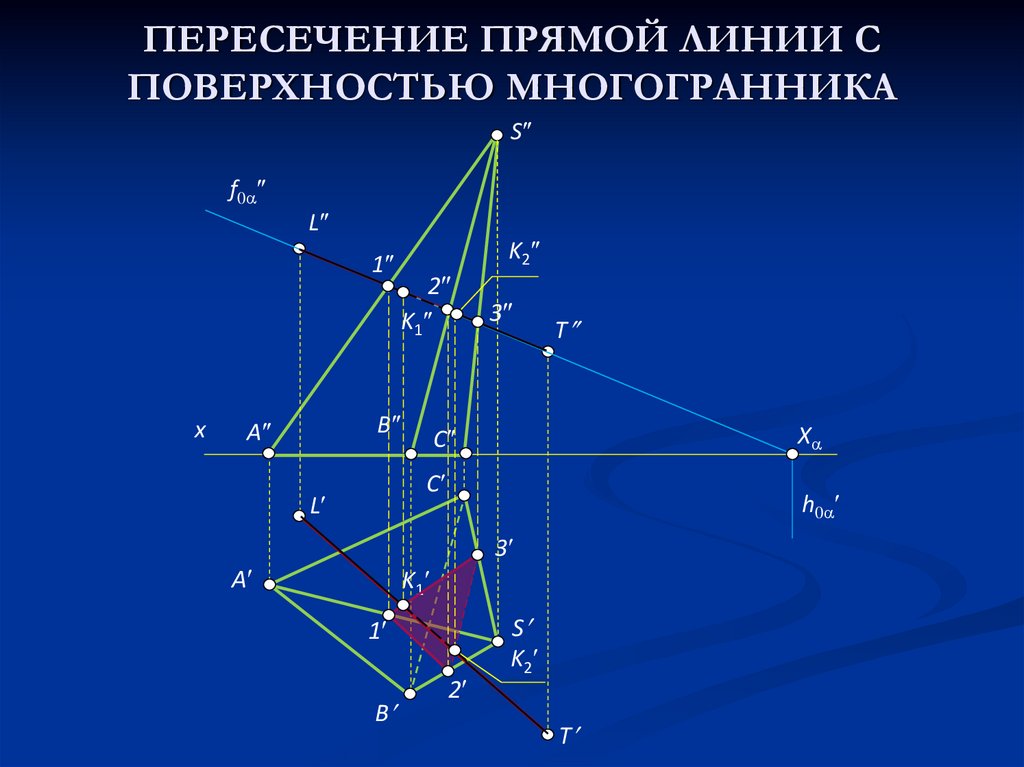
16. ПЕРЕСЕЧЕНИЕ ПРЯМОЙ ЛИНИИ С ПОВЕРХНОСТЬЮ МНОГОГРАННИКА
Для построения точек пересечения прямой линии споверхностью многогранника необходимо:
1) через прямую провести любую вспомогательную
плоскость;
2) построить сечение многогранника этой
вспомогательной плоскостью;
3) найти искомые точки в пересечении прямой с
контурами построенного сечения.
17. ПЕРЕСЕЧЕНИЕ ПРЯМОЙ ЛИНИИ С ПОВЕРХНОСТЬЮ МНОГОГРАННИКА
Sf0
L
1
x
K2
2
K1
B
A
3
T
X
C
C
L
h0
3
K1
A
S
K2
1
B
2
T
18. ПЕРЕСЕЧЕНИЕ ПРЯМОЙ ЛИНИИ С ПОВЕРХНОСТЬЮ КОНУСА И ЦИЛИНДРА
Точки пересечения прямой линии с поверхностью конусаили цилиндра можно построить двумя способами.
Первый способ заключается в том, что в конус или цилиндр
вписывают соответственно пирамиду или призму, строят сечение
вписанного многогранника вспомогательной плоскостью и
полученные точки на ребрах соединяют плавной кривой. Точки
пересечения прямой с построенным сечением есть точки
пересечения
этой
прямой
с
поверхностью
заданного
геометрического тела. В результате получаем приближенное
решение задачи.
Для получения точного решения вспомогательную плоскость
нужно выбрать так, чтобы полученное сечение линейчатой
поверхности представляло собой простейшую фигуру –
многоугольник. В случае конической поверхности такая плоскость
должна проходить через заданную прямую и вершину конуса, тогда
треугольник.
в сечении образуется
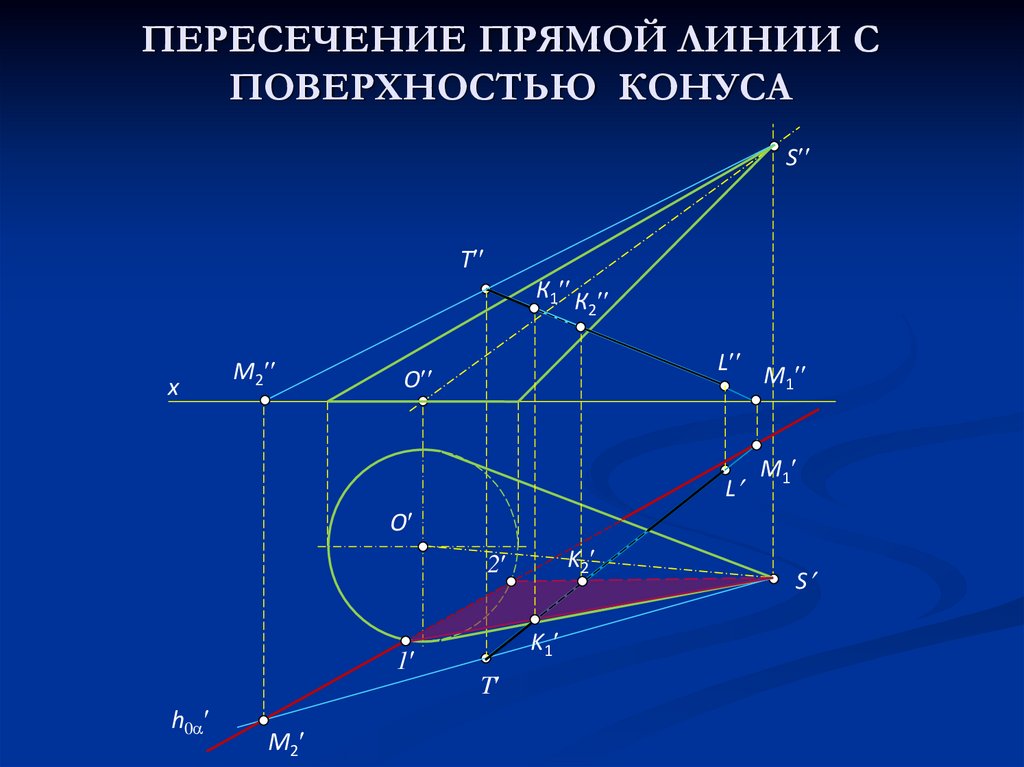
19. ПЕРЕСЕЧЕНИЕ ПРЯМОЙ ЛИНИИ С ПОВЕРХНОСТЬЮ КОНУСА
ST
x
M2
К1 К
2
L M
1
O
L
M1
O
K2
2
K1
1
T
h0
M2
S
20.
ПЕРЕСЕЧЕНИЕ ПРЯМОЙ ЛИНИИ СПОВЕРХНОСТЬЮ ЦИЛИНДРА
Для получения точного решения в качестве вспомогательной
плоскости выбираем плоскость общего положения, параллельную
оси цилиндра, и задаем ее двумя пересекающимися прямыми –
прямой LT и произвольной прямой, параллельной оси. Такую
прямую можно провести через любую точку прямой LT.
Горизонтальная проекция прямой параллельна О1 О2 , а
фронтальная проекция – О1 О2 .
Поскольку вспомогательная плоскость выбрана параллельной
оси цилиндра, сечение будет представлять собой параллелограмм.
21. ПЕРЕСЕЧЕНИЕ ПРЯМОЙ ЛИНИИ С ПОВЕРХНОСТЬЮ ЦИЛИНДРА
О2L
x
M2
K1
K2
T
О1
M1
M1
О1
2
T
К2
1
h0
3
К1
M2
L
О2
4

















 mathematics
mathematics