Similar presentations:
Многогранники и тела вращения
1. Многогранники
2.
ПРИЗМАA2
(n-угольная) это многогранник, у которой
одна грань n-угольник, а
остальные n-граней –
ПАРАЛЛЕЛОГРАММЫ
A3
A1
An
An-1
Элементы призмы:
1.Грань
2.Ребро
3.Высота
4.Основание
5.Боковая
поверхность
.
H
B2
B3
O
B1
Bn
Bn-1
β
3.
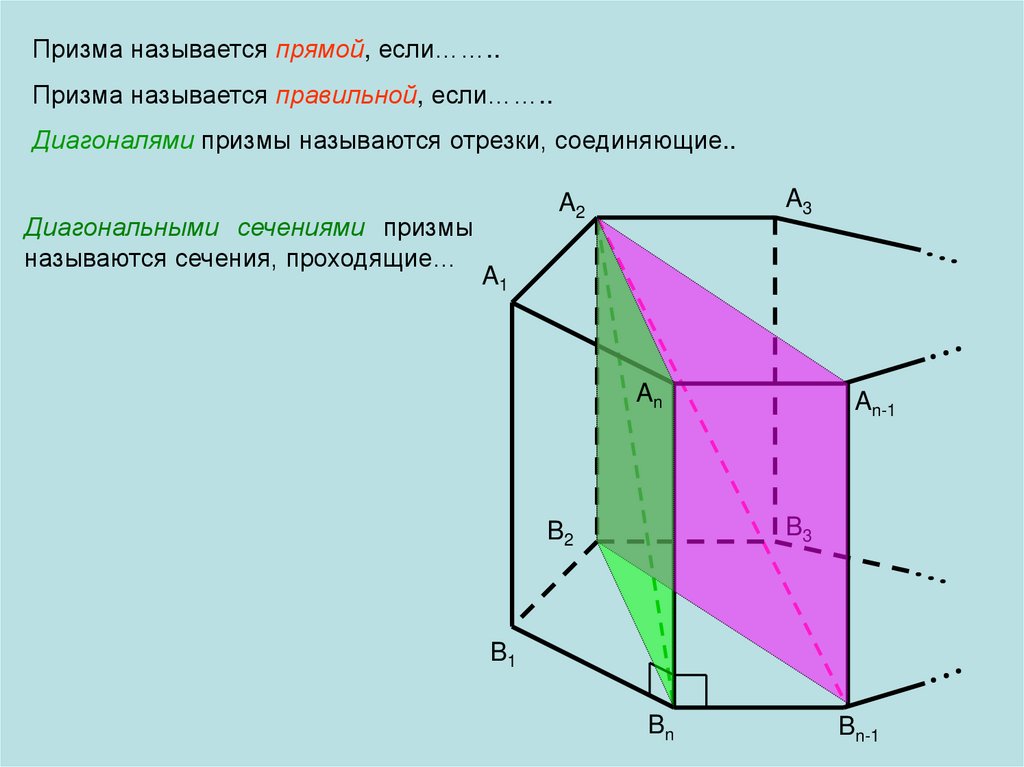
Призма называется прямой, если……..Призма называется правильной, если……..
Диагоналями призмы называются отрезки, соединяющие..
Диагональными сечениями призмы
называются сечения, проходящие…
A3
A2
A1
An
An-1
B3
B2
B1
Bn
Bn-1
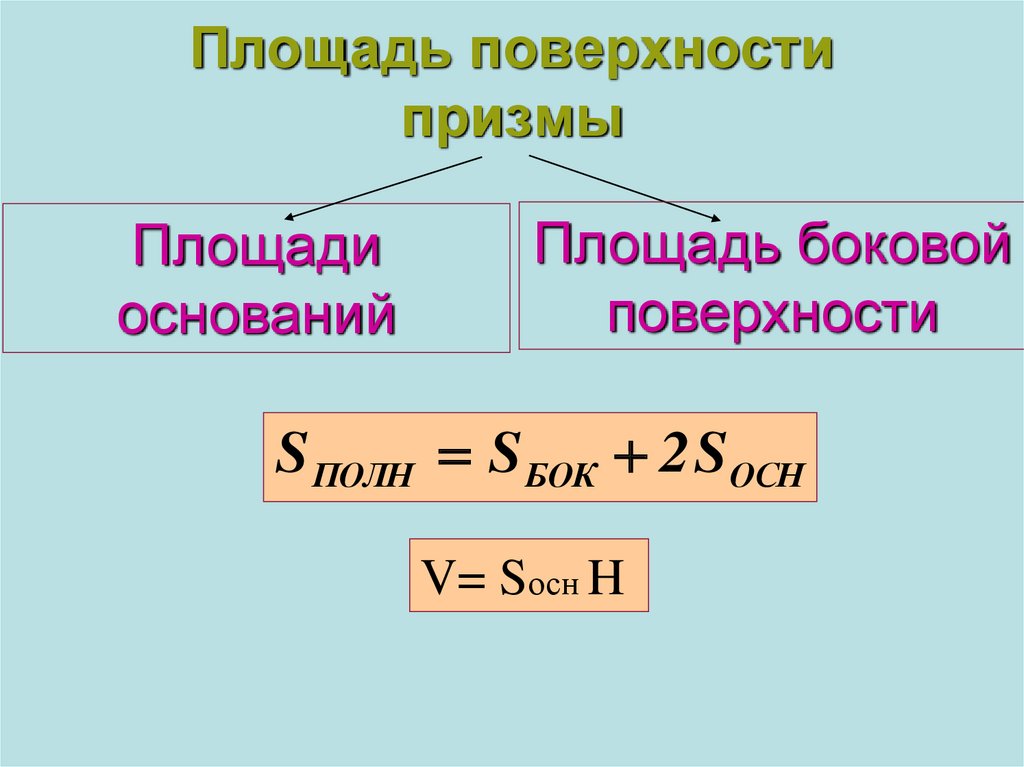
4. Площадь поверхности призмы
Площадиоснований
Площадь боковой
поверхности
S ПОЛН S БОК 2 SОСН
V= Sосн H
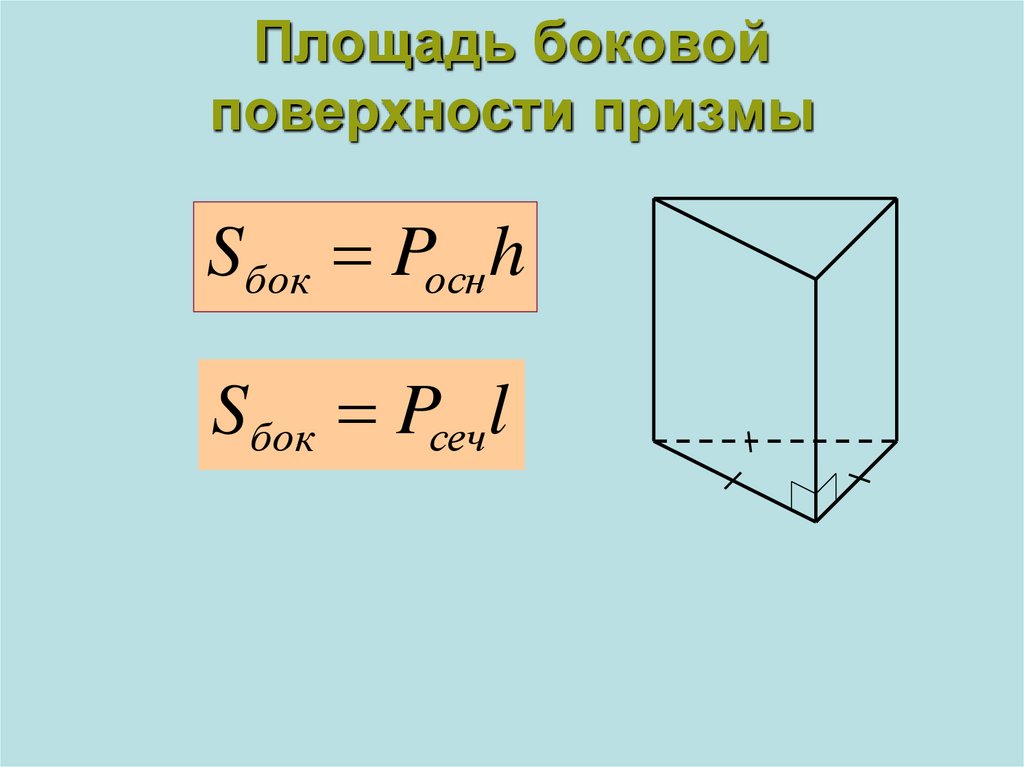
5. Площадь боковой поверхности призмы
Sбок Pосн hSбок Pсеч l
6.
Параллелепипед - это призма, основаниеявляется ПАРАЛЛЕЛОГРАМОМ.
Параллелепипед называется прямым, если…
Параллелепипед называется прямоугольным, если…
которой
7.
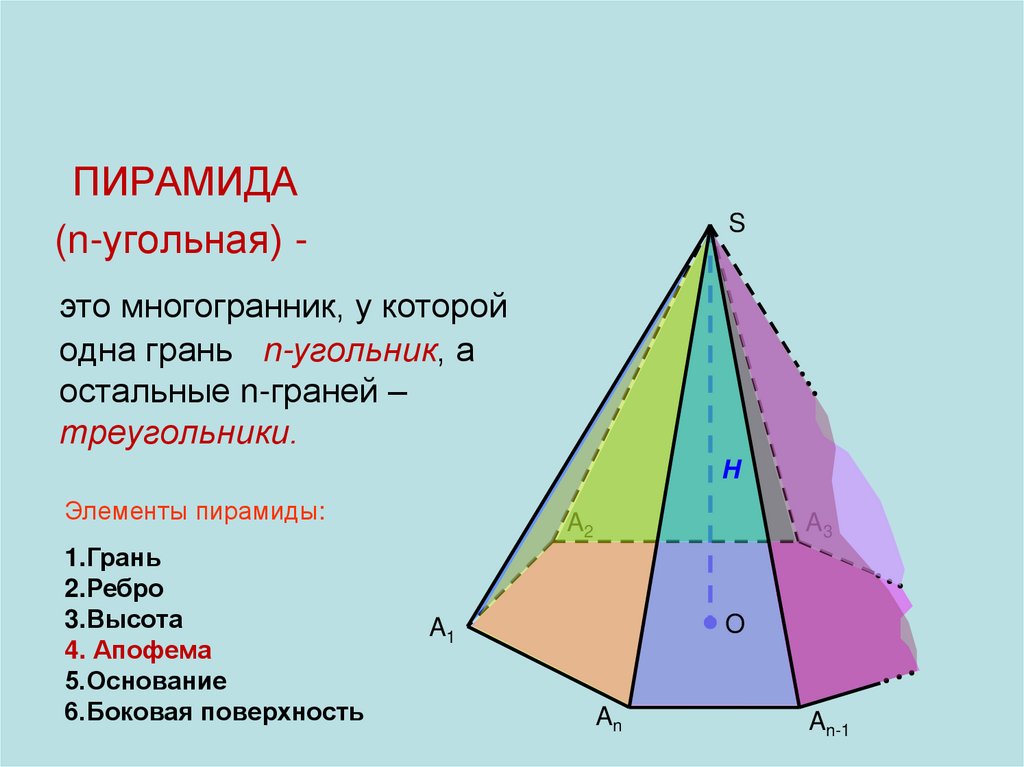
ПИРАМИДА(n-угольная) -
S
это многогранник, у которой
одна грань n-угольник, а
остальные n-граней –
треугольники.
H
Элементы пирамиды:
1.Грань
2.Ребро
3.Высота
4. Апофема
5.Основание
6.Боковая поверхность
A2
A3
O
A1
An
An-1
8.
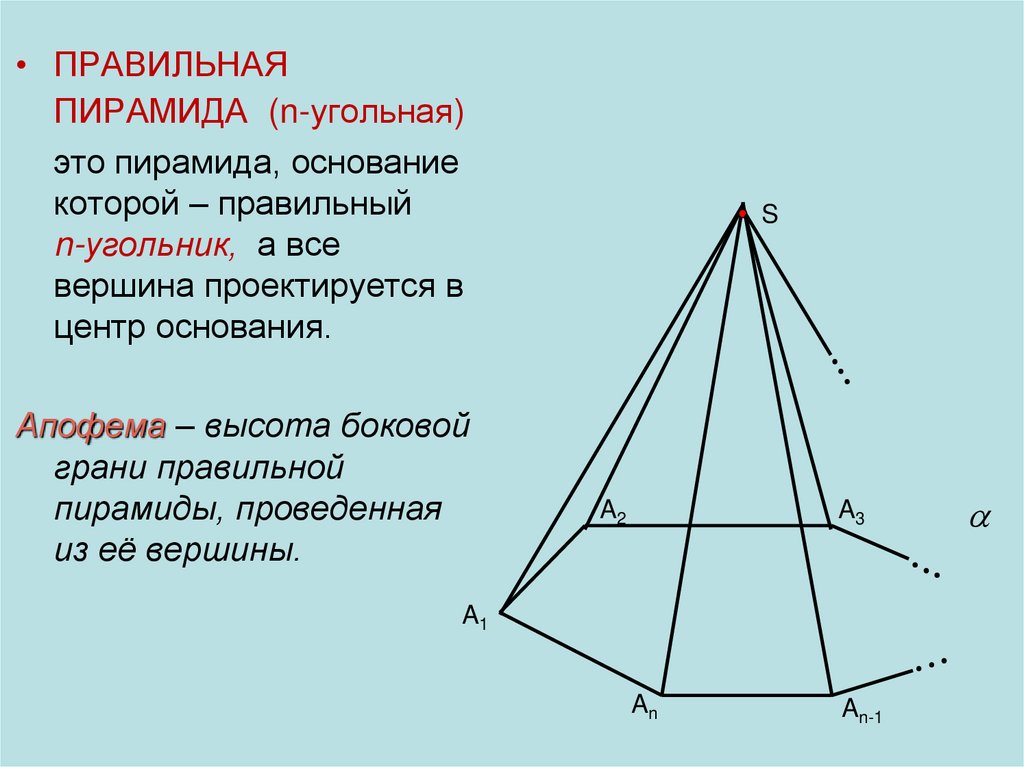
• ПРАВИЛЬНАЯПИРАМИДА (n-угольная)
это пирамида, основание
которой – правильный
n-угольник, а все
вершина проектируется в
центр основания.
Апофема – высота боковой
грани правильной
пирамиды, проведенная
из её вершины.
S
A2
A3
A1
An
An-1
9. Площадь поверхности пирамиды
Площадьоснования
Площадь боковой
поверхности
S ПОЛН S БОК SОСН
V= 1/3 Sосн H
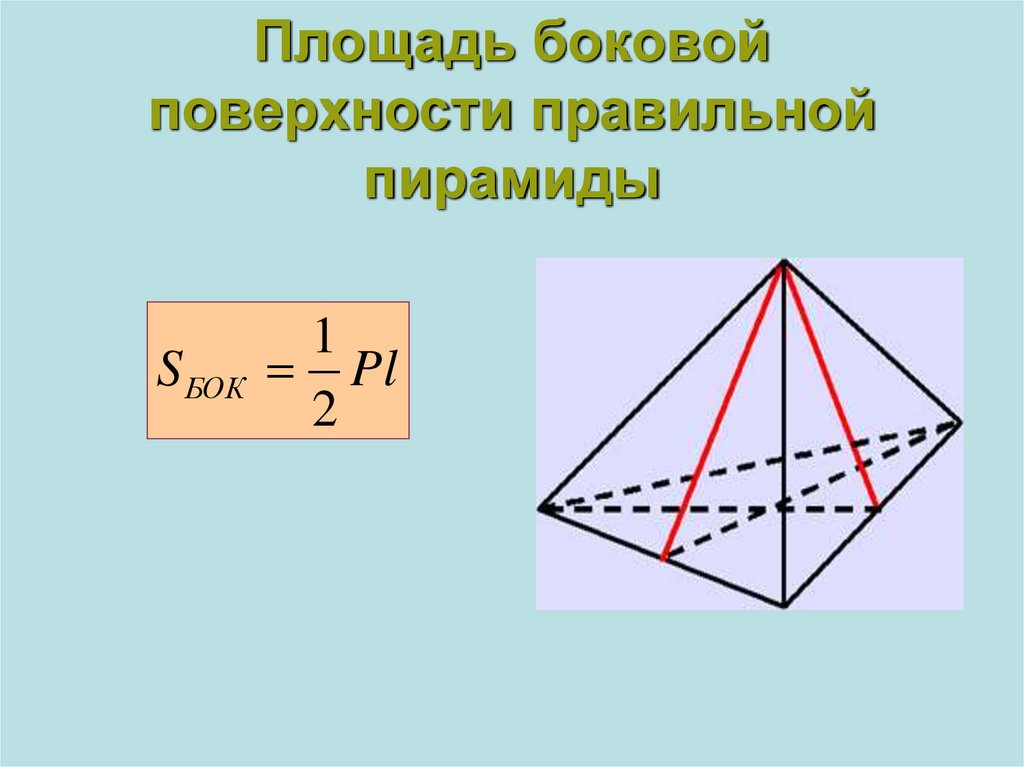
10. Площадь боковой поверхности правильной пирамиды
S БОК1
Pl
2
11.
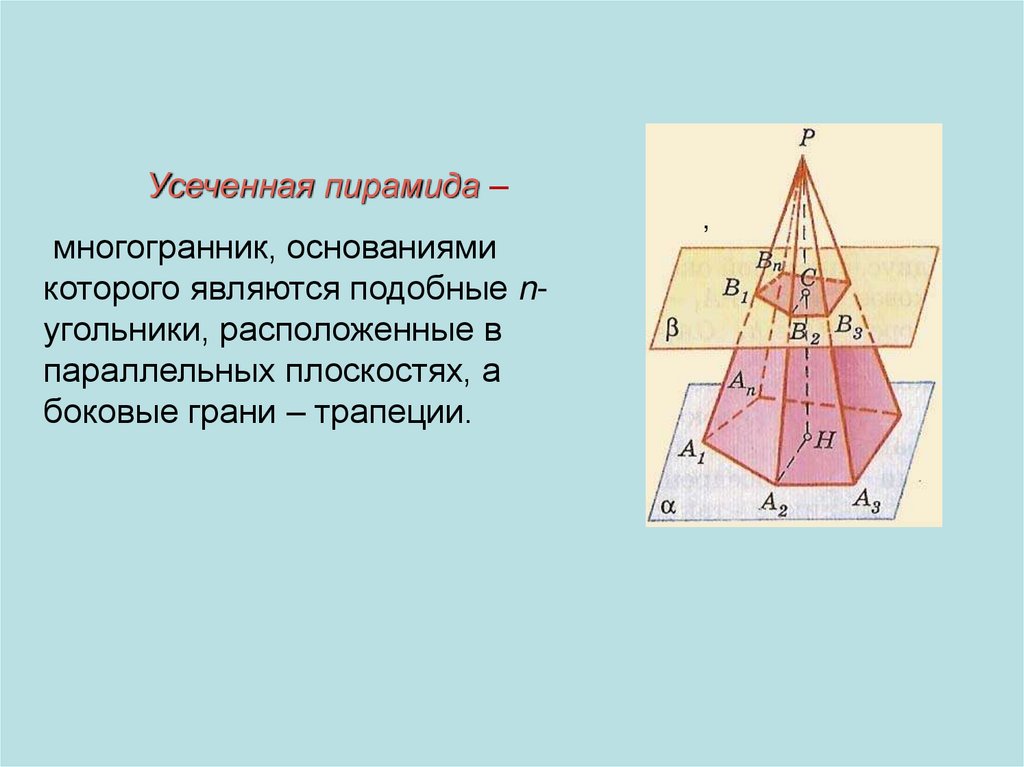
Усеченная пирамида –многогранник, основаниями
которого являются подобные nугольники, расположенные в
параллельных плоскостях, а
боковые грани – трапеции.
,
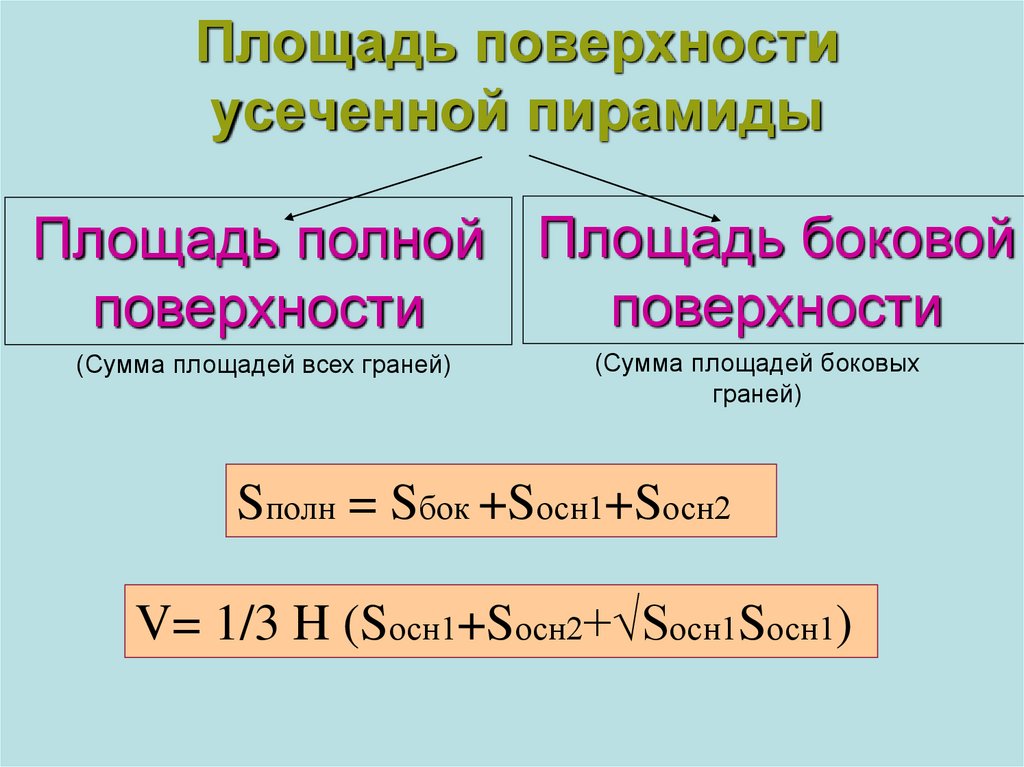
12. Площадь поверхности усеченной пирамиды
Площадь полной Площадь боковойповерхности
поверхности
(Сумма площадей всех граней)
(Сумма площадей боковых
граней)
Sполн = Sбок +Sосн1+Sосн2
V= 1/3 H (Sосн1+Sосн2+√Sосн1Sосн1)
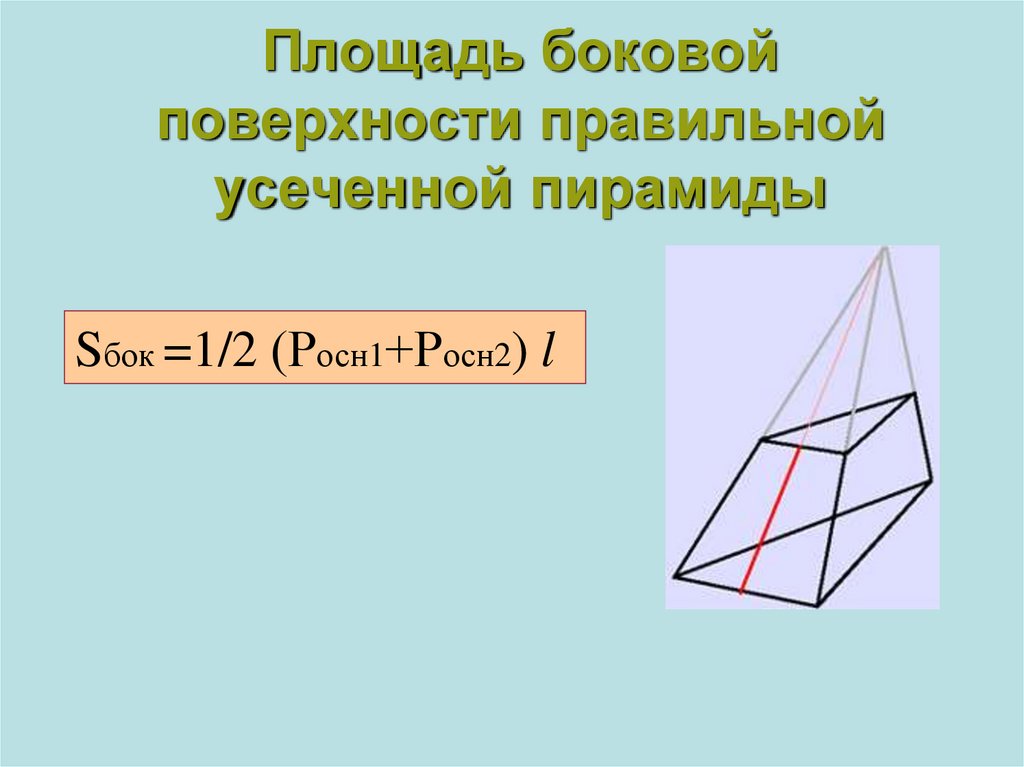
13. Площадь боковой поверхности правильной усеченной пирамиды
Sбок =1/2 (Росн1+Росн2) l14. Тела вращения
15.
16.
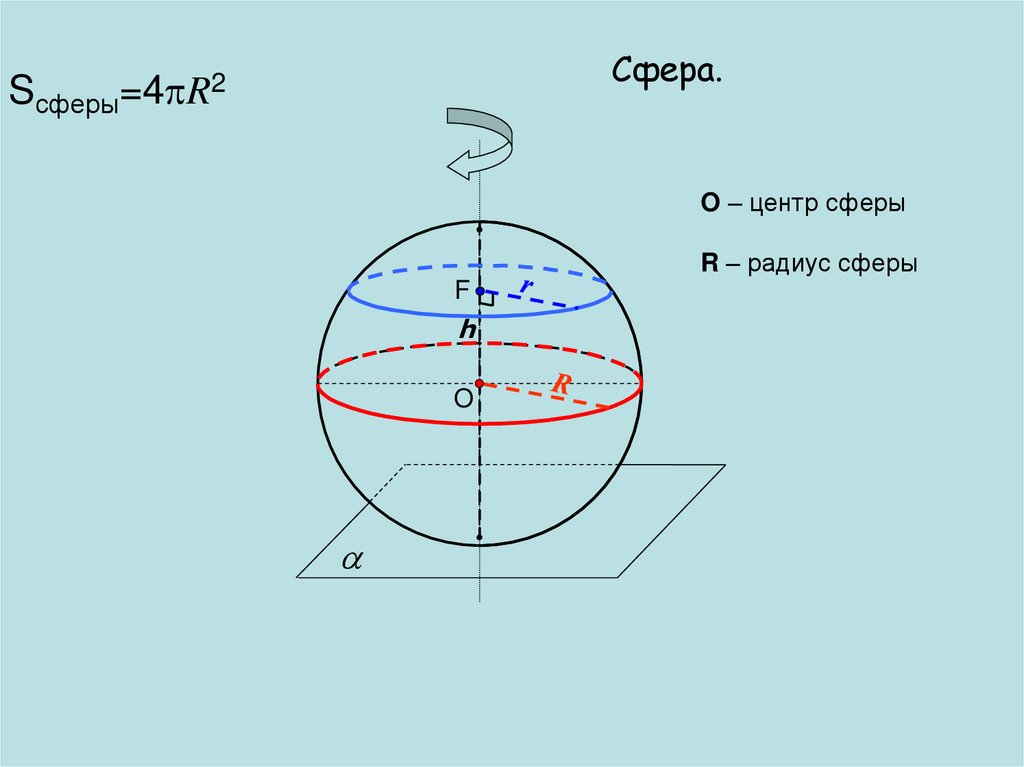
SсферыСфера.
=4 R2
O – центр сферы
R – радиус сферы
F
h
O
17.
18.
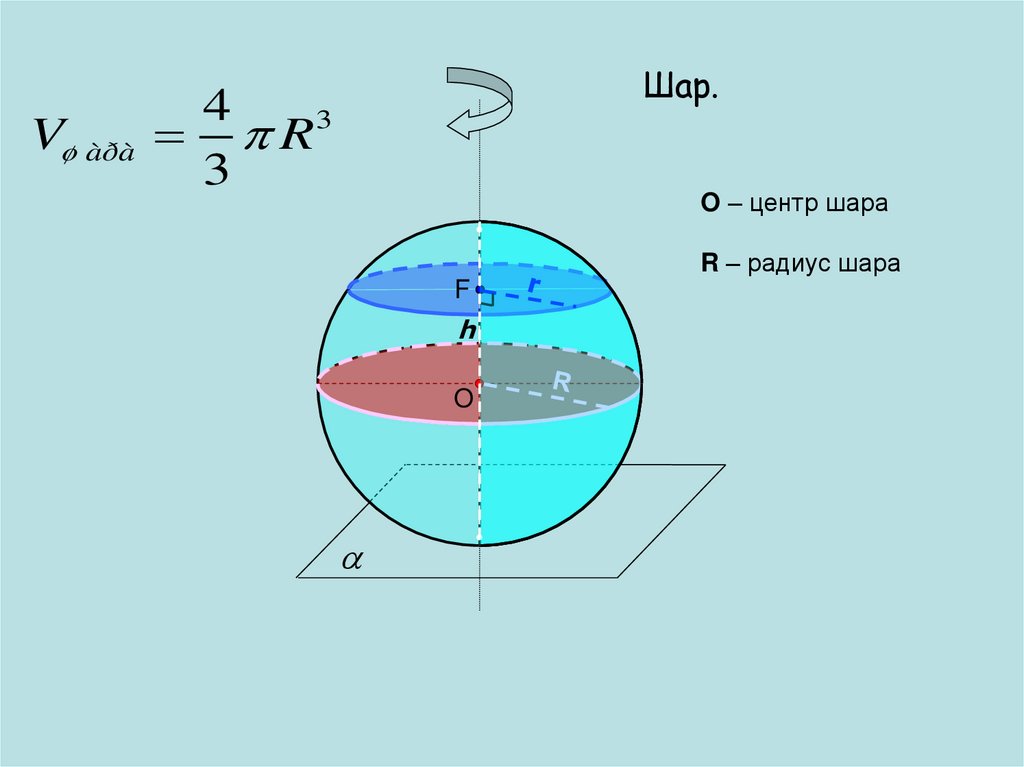
Vø àðàШар.
4
3
R
3
O – центр шара
R – радиус шара
F
h
O
19.
O20.
21.
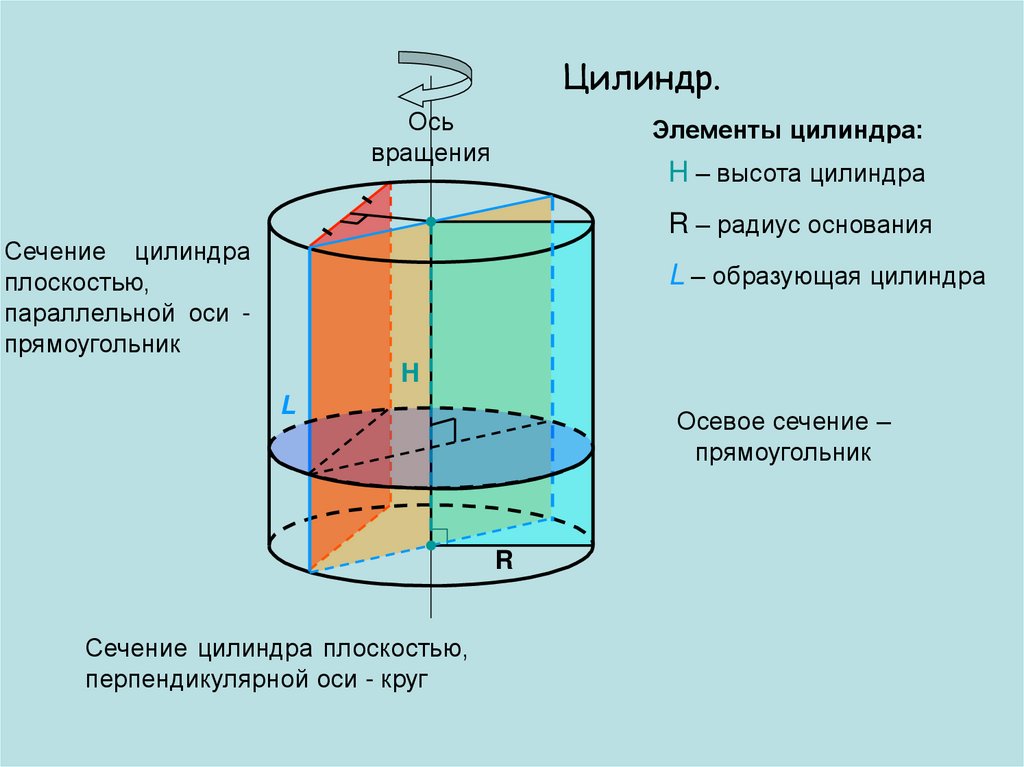
Цилиндр.Ось
вращения
Элементы цилиндра:
H – высота цилиндра
R – радиус основания
Сечение цилиндра
плоскостью,
параллельной оси прямоугольник
L – образующая цилиндра
H
L
Осевое сечение –
прямоугольник
R
Сечение цилиндра плоскостью,
перпендикулярной оси - круг
22.
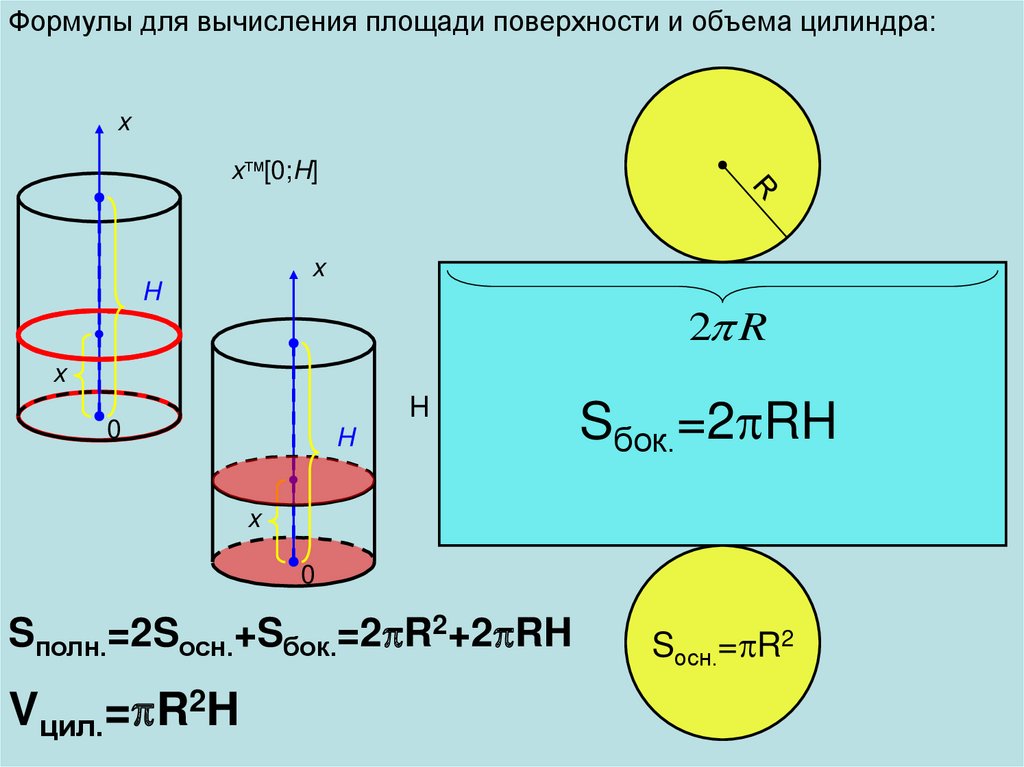
Формулы для вычисления площади поверхности и объема цилиндра:x
x [0;H]
x
H
2 R
x
H
0
H
Sбок.=2 RH
x
0
Sполн.=2Sосн.+Sбок.=2 R2+2 RH
Vцил.= R2H
Sосн.= R2
23.
Конус.Ось
вращения
Элементы конуса:
H – высота конуса
R – радиус основания
L – образующая конуса
Сечением конуса плоскостью,
перпендикулярной
высоте
(параллельной
основанию)
является круг.
H
L
R
Осевое сечение конуса – равнобедренный треугольник
r
– радиус сечения.
24.
Формулы для вычисления площади поверхности и объема конуса:L
Sосн.= R2
R
Sпов.=Sбок.+Sосн.= RL+ R2= R(L+R)
1
1 2
V Sî ñí . H R H
3
3
25.
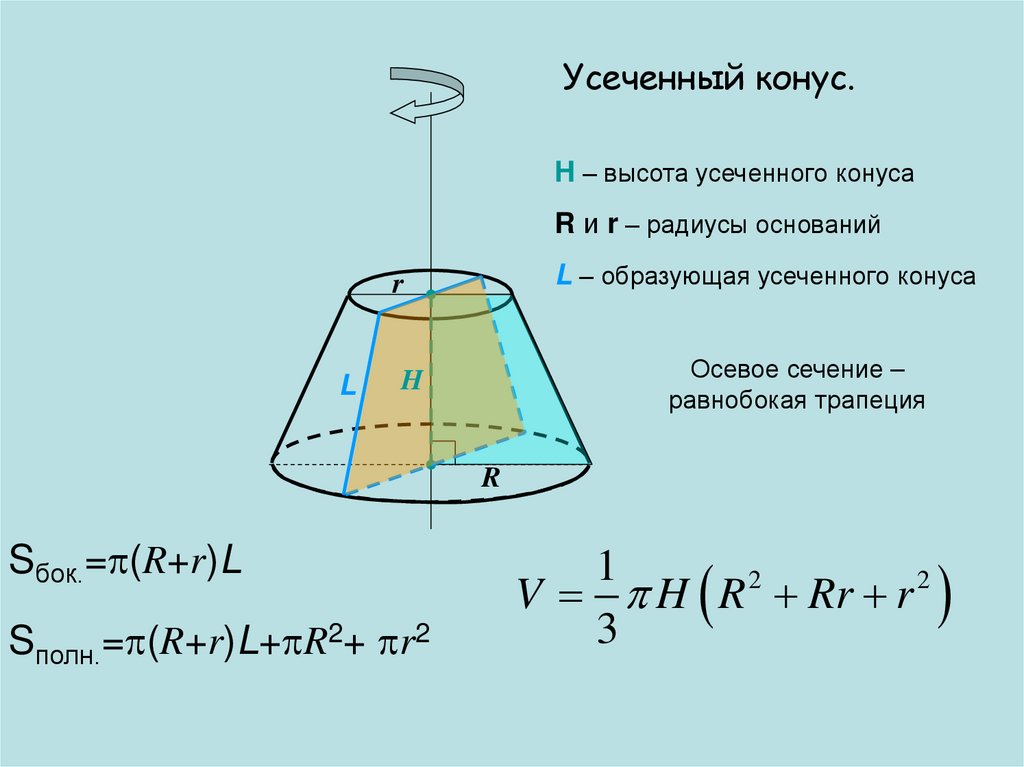
Усеченный конус.H – высота усеченного конуса
R и r – радиусы оснований
L – образующая усеченного конуса
r
L
Осевое сечение –
равнобокая трапеция
H
R
Sбок.= (R+r)L
Sполн.= (R+r)L+ R2+ r2
1
V H R 2 Rr r 2
3
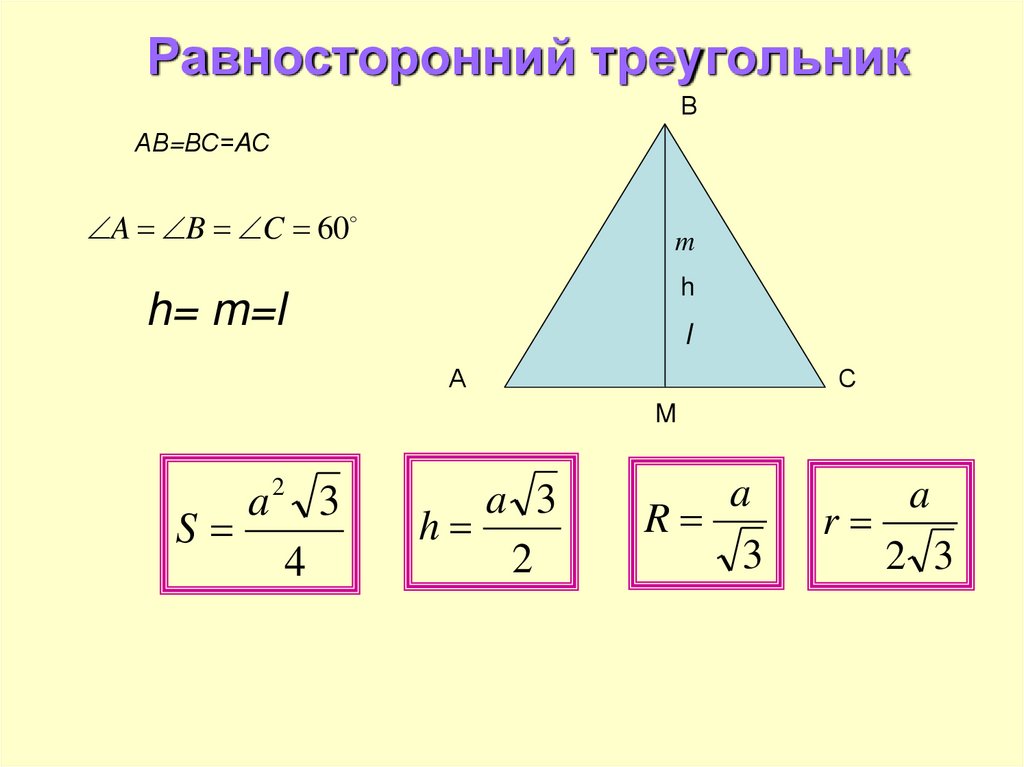
26. Равносторонний треугольник
ВАВ=ВС=AС
A B C 60
m
h
h= m=l
l
А
С
M
a2 3
S
4
a 3
h
2
a
R
3
r
a
2 3
27. Равнобедренный треугольник
ВАВ=ВС
A B
m
h
hс= mс=lс
l
А
С
M
28. Теорема Пифагора
В прямоугольном треугольнике квадратгипотенузы равен сумме квадратов катетов:
c a b
2
В
2
c
а
С
2
b
А
a
sin ;
c
b
сos ;
c
tg
a
b
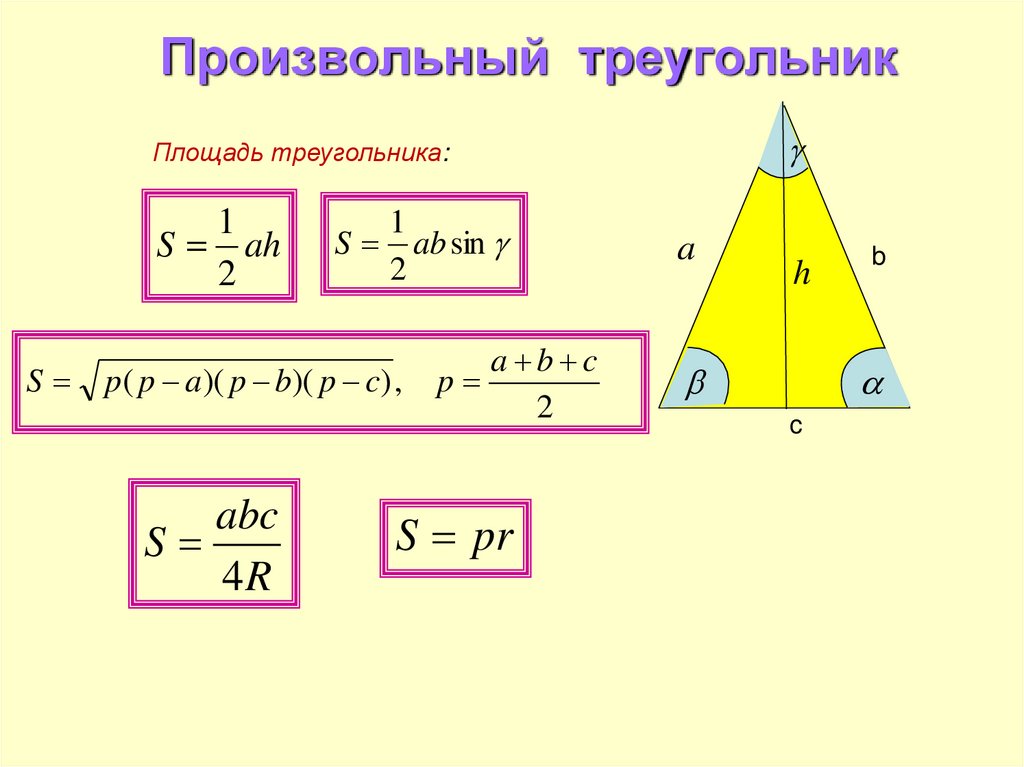
29. Произвольный треугольник
Площадь треугольника:1
S ah
2
S
S
1
ab sin
2
p( p a)( p b)( p c) ,
abc
S
4R
p
a b c
2
S pr
a
h
b
c
30. Квадрат
S aa
r
2
2
2
d
S
2
d
R
2
d
a
d a 2
31. Параллелограмм
S ah S ab sind1d 2 sin
S
2
d12 d 22 a 2 b 2 c 2 d 2
d1
h
a
d2
b
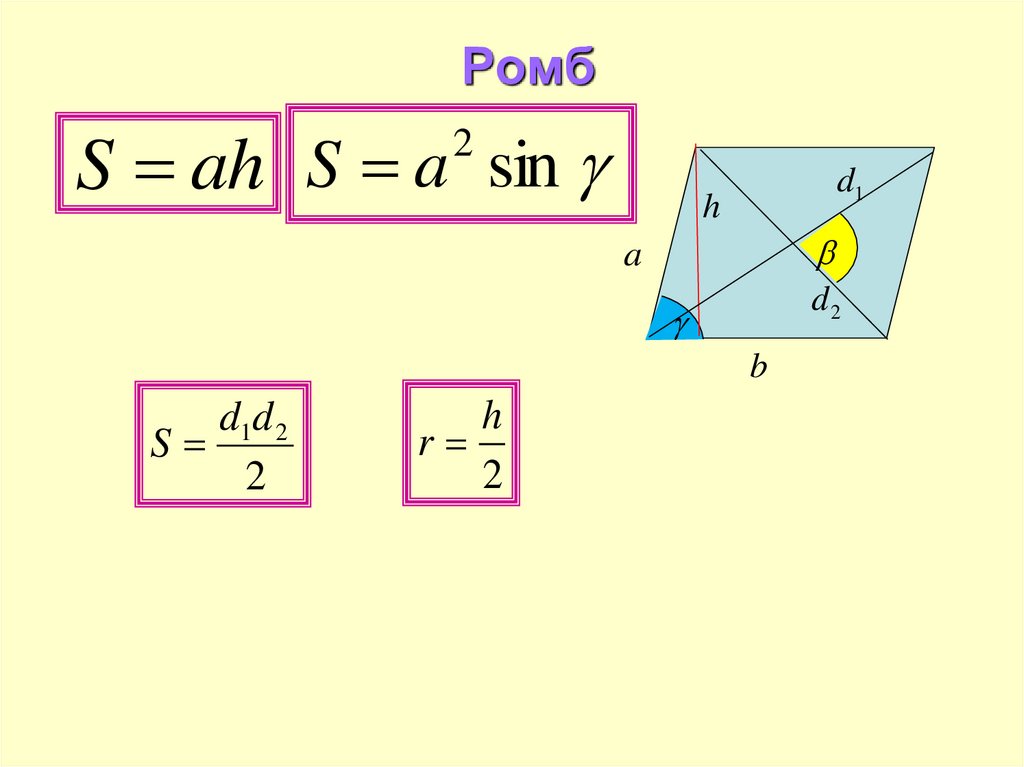
32. Ромб
S ah S a sin2
d1
h
d2
a
b
d1d 2
S
2
h
r
2
33. Трапеция
a bd1d 2 sin
S
h S
2
2
a b
MN
2
M
b
d1
h
N
d2
a















 mathematics
mathematics








