Термодинамика. Работа и теплопередача. (Лекция 7)

1.

ТЕРМОДИНАМИКА
РАБОТА И ТЕПЛОПЕРЕДАЧА
Рассмотрим газ, находящийся в цилиндрическом сосуде,
и отделенный от атмосферы поршнем площадью S

2.

Если газ, расширяясь, передвигает поршень на расстояние
dL, то он производит над ним работу:
dA F dL p S dL p dV,
где dV = S dL - изменение объема газа.
Полную работу А, совершаемую газом при изменении
его объема от V1 до V2, найдем путем интегрирования:
V2
A p dV
V1

3.

Работа газа зависит от траектории перехода из начального
состояния в конечное:
Графическое представление работы

4.

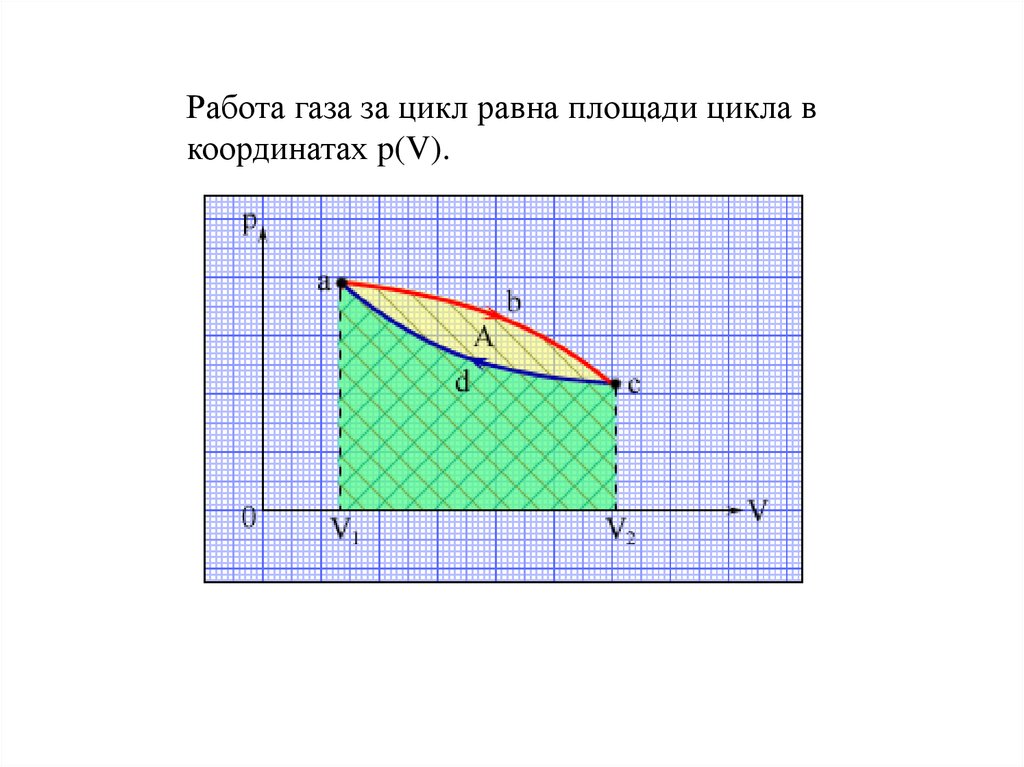
Работа газа за цикл равна площади цикла в
координатах p(V).

5.

Теплопередача - процесс обмена энергией между системой
и окружающими ее телами, не сопровождающийся
изменением внешних параметров состояния системы. Это
процесс передачи энергии неупорядоченного движения от
одних тел к другим.
Энергия, получаемая или отдаваемая системой в процессе
теплопередачи называется количеством тепла Q (1 Дж).
Передача энергии от системы к внешним телам с
изменением внешних макроскопических параметров
называется работой.

6.

СТЕПЕНИ СВОБОДЫ СИСТЕМЫ. РАСПРЕДЕЛЕНИЕ
ЭНЕРГИИ ХАОТИЧЕСКОГО ДВИЖЕНИЯ МОЛЕКУЛ
ПО СТЕПЕНЯМ СВОБОДЫ.
Выражение для средней энергии молекул E = 3/2 kT
учитывает только энергию поступательного движения
молекул. Однако наряду с поступательным движением
возможны так же вращение молекулы и колебания атомов,
входящих в состав молекул.

7.

Число степеней свободы материального объекта - это
число независимых координат, которые однозначно
задают положение объекта в пространстве (или число
независимых
движений,
которые
однозначно
определяют энергию объекта):
i = iпост. + iвращ. + iколеб.

8.

Материальная точка. Положение материальной
точки в пространстве полностью определяется
заданием значений трех её координат. Поэтому
материальная точка имеет три поступательных
степени свободы:
i=3

9.

Две материальные точки с жесткой связью.
Такая система может совершать поступательное
движение в трех направлениях и вращаться вокруг
двух осей. Следовательно, она имеет пять степеней
свободы – 3 поступательных и 2 вращательных:
i=5

10.

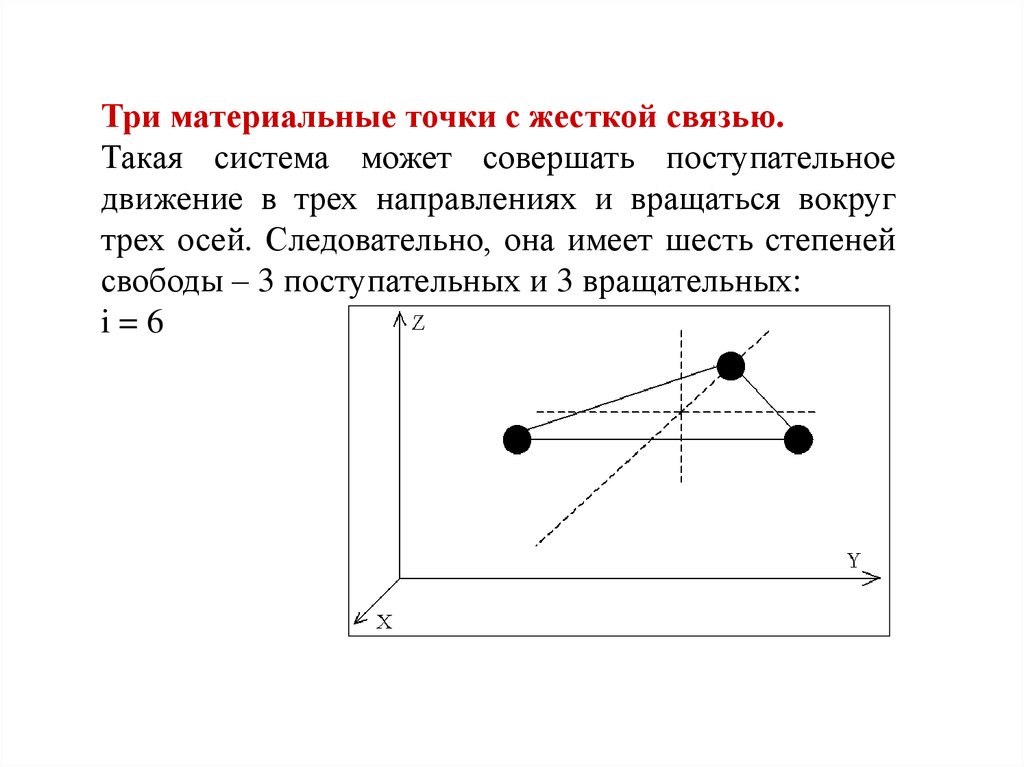
Три материальные точки с жесткой связью.
Такая система может совершать поступательное
движение в трех направлениях и вращаться вокруг
трех осей. Следовательно, она имеет шесть степеней
свободы – 3 поступательных и 3 вращательных:
i=6

11.

i i пост. i вращ. 2 i колеб.
Две материальные точки с упругой связью. Такая
система имеет шесть степеней свободы: 3 поступательных,
2 вращательных и 1 колебательную.

12.

ЗАКОН РАВНОМЕРНОГО РАСПРЕДЕЛЕНИЯ
ЭНЕРГИИ ПО СТЕПЕНЯМ СВОБОДЫ МОЛЕКУЛ
Выражение для средней энергии молекул E = 3/2 kT учитывает
только энергию поступательного движения молекул.
Энергия, приходящаяся на каждую поступательную
степень свободы равна:
1
E kT
2

13.

Средняя энергия хаотического теплового движения
одной молекулы равна:
i
E kT
2
Закон Больцмана о равномерном распределении
энергии по степеням свободы:
На каждую поступательную и вращательную степень
свободы приходится в среднем энергия kT/2, а на каждую
колебательную степень свободы - энергия kT.
На колебательную степень свободы приходится удвоенная
энергия, так как колеблющаяся частица обладает как
потенциальной, так и кинетической энергией, средние
значения которых одинаковы и равны kT/2.

14.

ВНУТРЕННЯЯ ЭНЕРГИЯ ИДЕАЛЬНОГО ГАЗА.
Энергия, связанная с внутренними движениями частиц
системы и их взаимодействиями между собой, называется
внутренней энергией системы. Под внутренней энергией
идеального газа понимают энергию хаотического
движения его молекул.

15.

Определим внутреннюю энергию идеального газа:
i m
U RT
2
i m
U R T
2
i m
dU R dT
2
Внутренняя энергия - функция температуры.

16.

ПЕРВОЕ НАЧАЛО ТЕРМОДИНАМИКИ
I начало термодинамики говорит о сохранении полной
энергии.
Количество тепла, сообщенное системе, расходуется на
приращение внутренней энергии системы и на
совершение системой работы: Q = U + A
Количество теплоты Q - мера переданной энергии при
теплообмене.

17.

I начало термодинамики в дифференциальной форме:
dQ = dU + dA
dQ и dA нельзя рассматривать как приращения
величин Q и A.
Для записи элементарного количества тепла и
элементарной работы будем использовать другие символы
Q и A соответственно:
Q = dU + A

18.

Рассмотрим применение I начала термодинамики к
изопроцессам в газах:
Q = dU + A
Изобарический процесс:
V2
V2
V1
V1
A p dV p dV p V2 V1 P V
Подводимое к газу тепло затрачивается на изменение
внутренней энергии системы и на совершение им работы.
Q dU pdV

19.

Изохорический процесс: Q = dU
( A = 0, т.к. V = const)
При изохорическом процессе подводимое к газу тепло
затрачивается на изменение внутренней энергии газа. Работа
расширения равна нулю.

20.

Изотермический процесс: Q = A
(dU = 0, т.к. T = const)
Q pdV
Подводимое к газу тепло при изотермическом процессе
затрачивается только на совершение работы.
V2
dV
V2
A R T
R T ln
V
V1
V1

21.

ТЕПЛОЕМКОСТЬ
Теплоемкостью тела (полной теплоемкостью)
называется физическая величина, численно равная
количеству тепла, которое надо сообщить телу, чтобы
нагреть его на один Кельвин:
Q
C0
dT
Дж
C0 1
К

22.

Удельной теплоемкостью вещества называется
физическая величина, численно равная количеству
тепла, которое надо сообщить 1 кг вещества, чтобы
нагреть его на один Кельвин :
Q
с
m dT
Дж
c 1
кг К

23.

Молярной теплоемкостью вещества называется
физическая величина, численно равная количеству
тепла, которое надо сообщить 1 молю вещества, чтобы
нагреть его на один Кельвин :
Q
Q
C
dT m dT
C c
Дж
C 1
моль К

24.

Различают теплоемкость для случаев, когда нагревание
происходит при постоянном объеме
(СV) или при
постоянном давлении (CP) .
Теплоемкость при постоянном объеме.
Если нагревание происходит при постоянном объеме,
система не совершает работы над внешними телами и,
следовательно,
согласно
первому
началу
термодинамики, все тепло идет на приращение
внутренней энергии тела:
Q = dU + A
А = 0
Q = dU

25.

Тогда молярная теплоемкость при постоянном объеме равна:
i
CV R
2

26.

Теплоемкость при постоянном давлении.
Если нагревание газа происходит при постоянном
давлении, то газ будет расширяться, совершая над
внешними телами положительную работу.
CP CV R

27.

Определим соотношение между теплоемкостями при
постоянном давлении и объеме:
i
CV R
2
i
i 2
CP R R
R
2
2
CP i 2
- коэффициент Пуассона
CV
i

28.

для одноатомного газа
CV
3
R,
2
5
C Р R.
2
для двухатомного газа
5
CV R,
2
7
C Р R.
2

29.

АДИАБАТИЧЕСКИЙ ПРОЦЕСС
Адиабатным (адиабатическим) называется процесс,
происходящий без теплообмена с окружающей средой.
Найдем уравнение, связывающее параметры идеального газа
при адиабатном процессе. Запишем первое начало
термодинамики Q = dU + A, учитывая следующее:
Q = 0
A = p dV
i m
m
dU R dT C V dT
2
m
C V dT p dV 0

30.

m
C V dT p dV 0
Из уравнения можно получить:
R CP CV CP
1 1
CV
CV
CV
показатель адиабаты или коэффициент Пуассона:
i 2
1
CV
i
Cp
Cp
CV

31.

Уравнение, связывающее параметры идеального газа при
адиабатном процессе.
TV
1
const
1
1
T1V
PV const
TP
1
const
1
2
T2 V
Уравнение Пуассона
(или уравнение
адиабатного процесса)

32.

р
адиабата
изотерма
V

33.

Определим работу газа в ходе адиабатного процесса:
0 = dU + A A = - dU
i
A R dT
2
T2
A C V dT C V T1 T2
T1
Это выражение для работы при адиабатическом
процессе можно преобразовать к виду:
1
1
V1
V1
p1V1
R T1
A
1
1
1 V2
1 V2