Similar presentations:
Системы логических уравнений. Метод отображений
1.
Системылогических
уравнений
Метод отображений
2.
Сколько существует различных наборовзначений логических переменных x1, x2,
… x10, которые удовлетворяют всем
перечисленным ниже условиям?
СИСТЕМЫ
ЛОГИЧЕСКИХ
УРАВНЕНИЙ
¬ (x1 ≡ x2) ∧ ((x1 ∧ ¬ x3) ∨ (¬ x1 ∧ x3)) = 0
¬ (x2 ≡ x3) ∧ ((x2 ∧ ¬ x4) ∨ (¬ x2 ∧ x4)) = 0
…
¬ (x8 ≡ x9) ∧ ((x8 ∧ ¬ x10) ∨ (¬ x8 ∧ x10)) = 0
В ответе не нужно перечислять все различные наборы значений
переменных x1, x2, … x10 при которых выполнена данная система
равенств. В качестве ответа Вам нужно указать количество таких
наборов.
3.
Запишем указанныеусловия в другой
системе
обозначений
Зная x1 и x2, можем найти все возможные
значения x3, удовлетворяющие первому
уравнению.
Рассуждая аналогичным образом, из известных
x2 и x3 можем найти x4, удовлетворяющее
второму уравнению.
Все уравнения,
входящие в систему,
однотипны, и в каждое
уравнение включено
три переменных.
То есть, зная пару (x1, x2) и определив значение x3, мы найдем пару (x2, x3),
которая, в свою очередь, приведет к паре (x3, x4) и так далее.
4.
Запишем указанныеусловия в другой
системе
обозначений
На каждом шаге имеем множество исходных
пар из набора (00, 01, 10, 11) и множество
полученных пар из такого же набора (00, 01,
10, 11).
Можно сказать, что исходное множество пар
отображается само в себя. Построим такое
отображение для данной системы.
Все уравнения,
входящие в систему,
однотипны, и в каждое
уравнение включено
три переменных.
5.
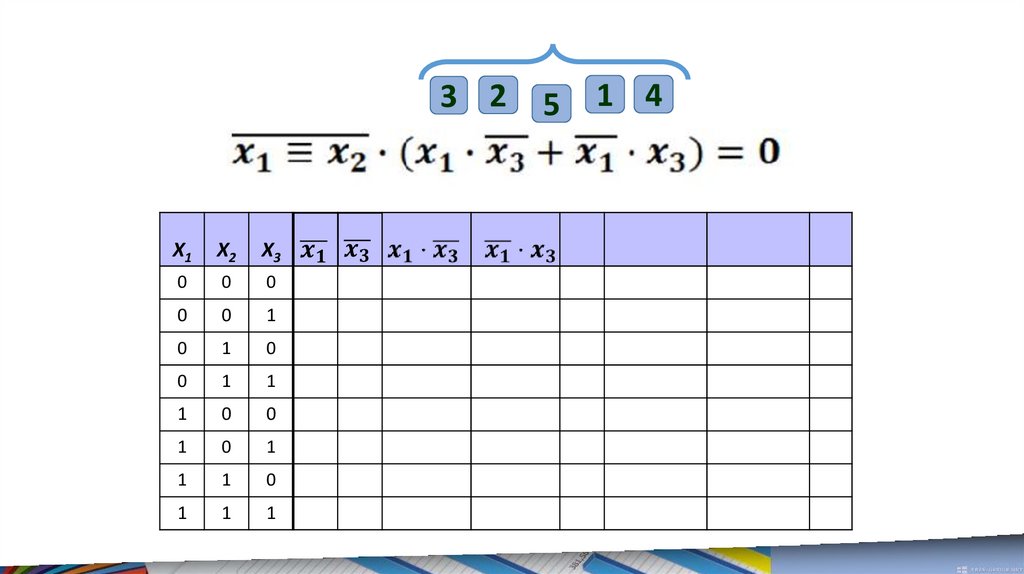
Сначала решим первое уравнение.Для этого заполним таблицу
истинности логического
выражения, записанного в левой
части.
Решить логическое
уравнение, значит
найти все значения
неизвестных, при
которых уравнение
превращается в верное
равенство.
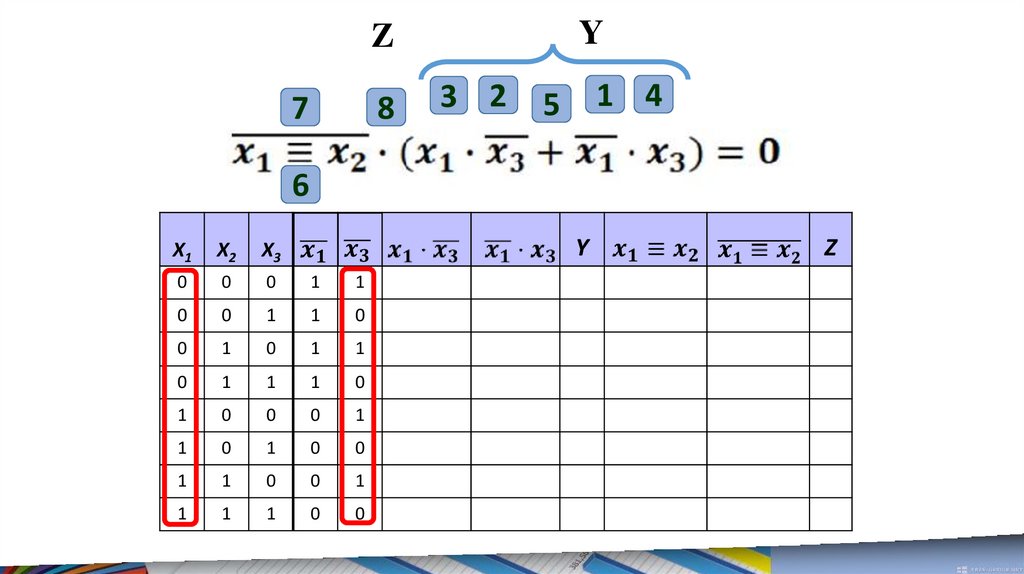
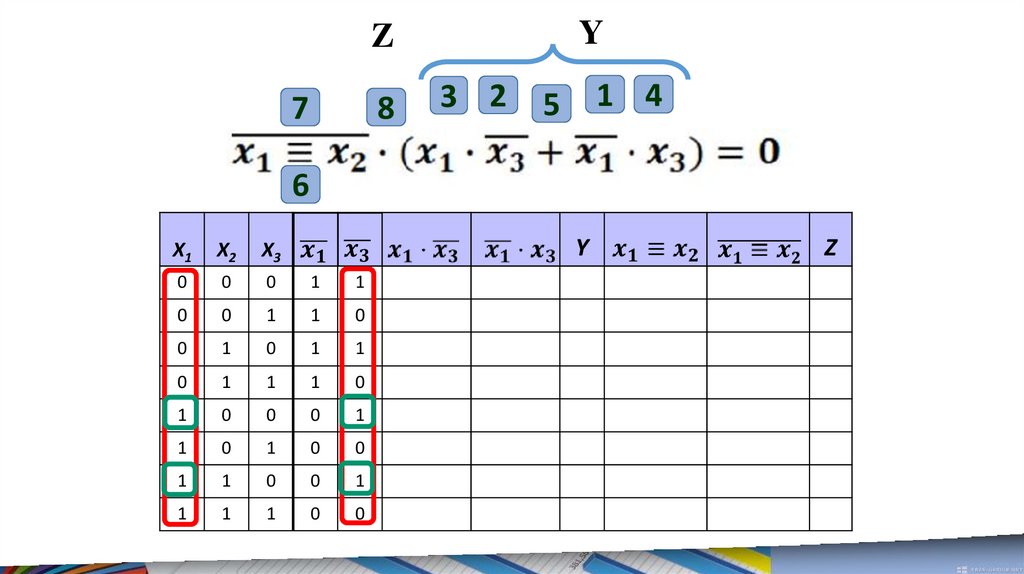
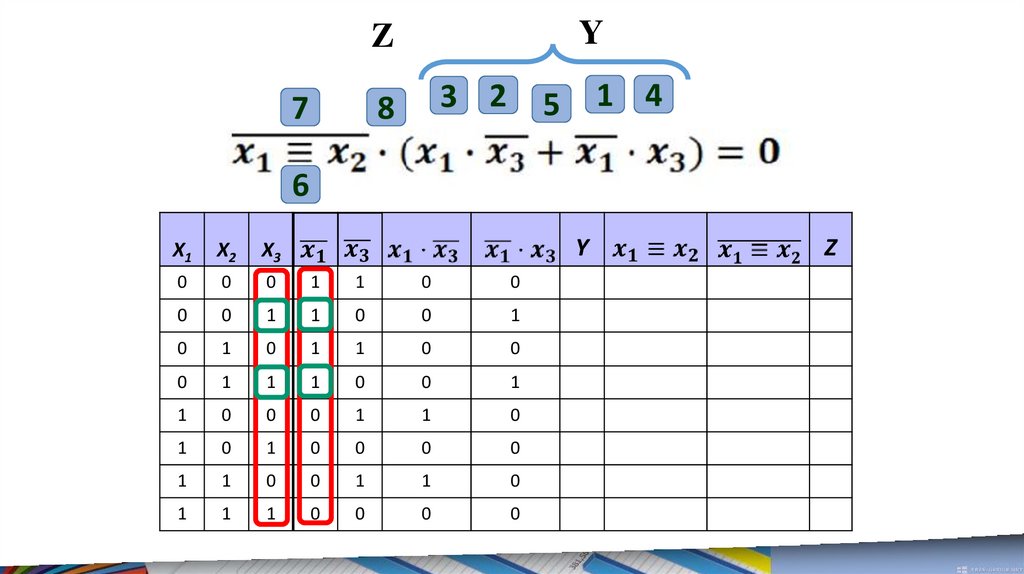
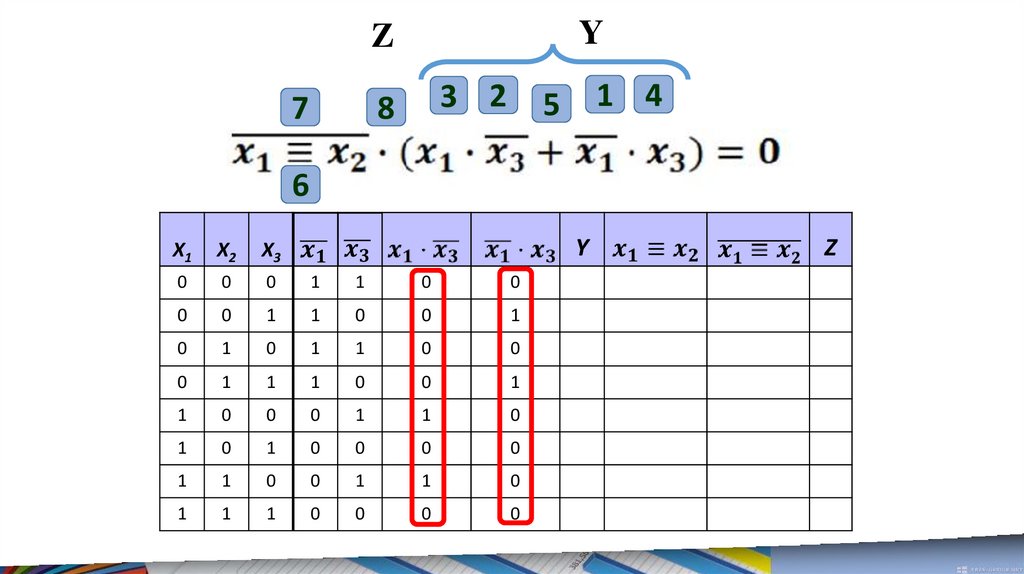
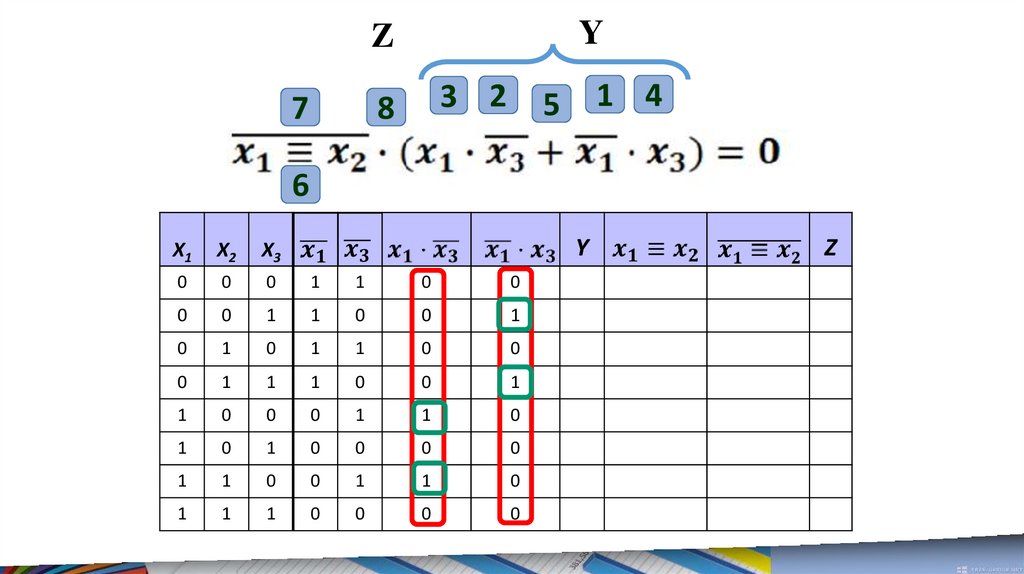
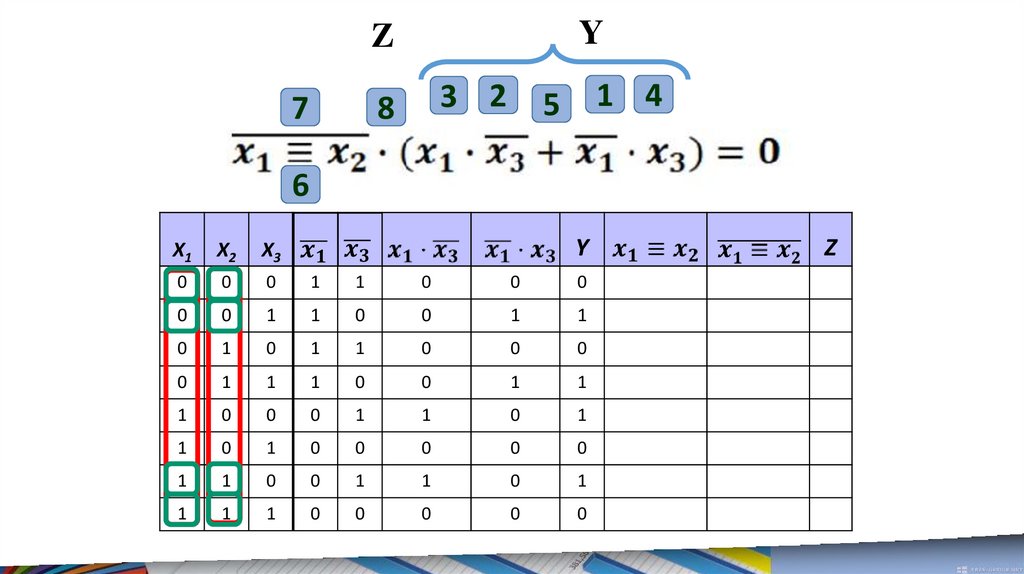
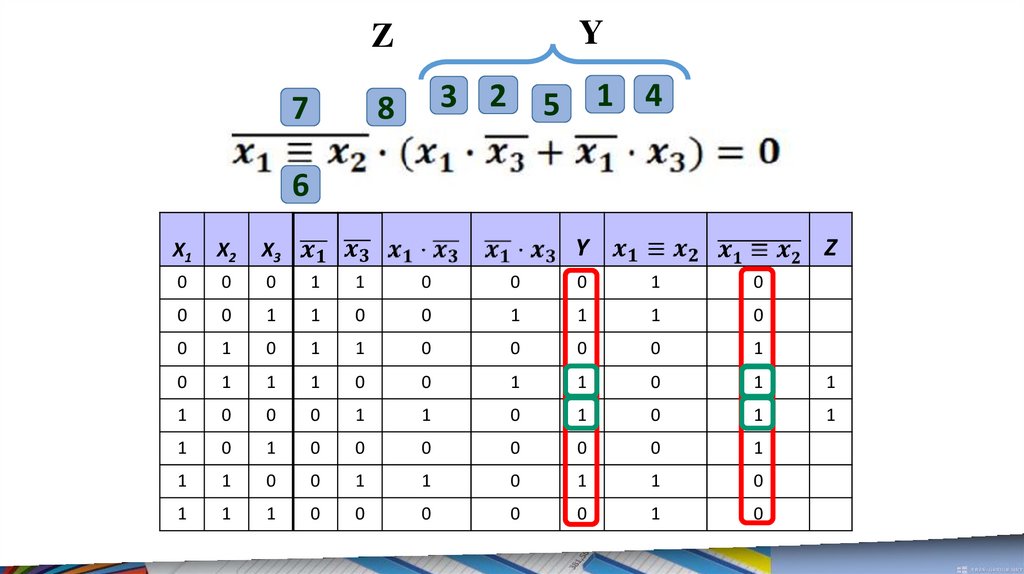
6.
Решим первое уравнение.В данном уравнении нужно найти такие x1, x2 и x3,
при которых левая часть принимает логическое
значение ЛОЖЬ.
7.
Построим таблицу истинностилогического выражения
X1
X2
X3
3
2 =
8
8.
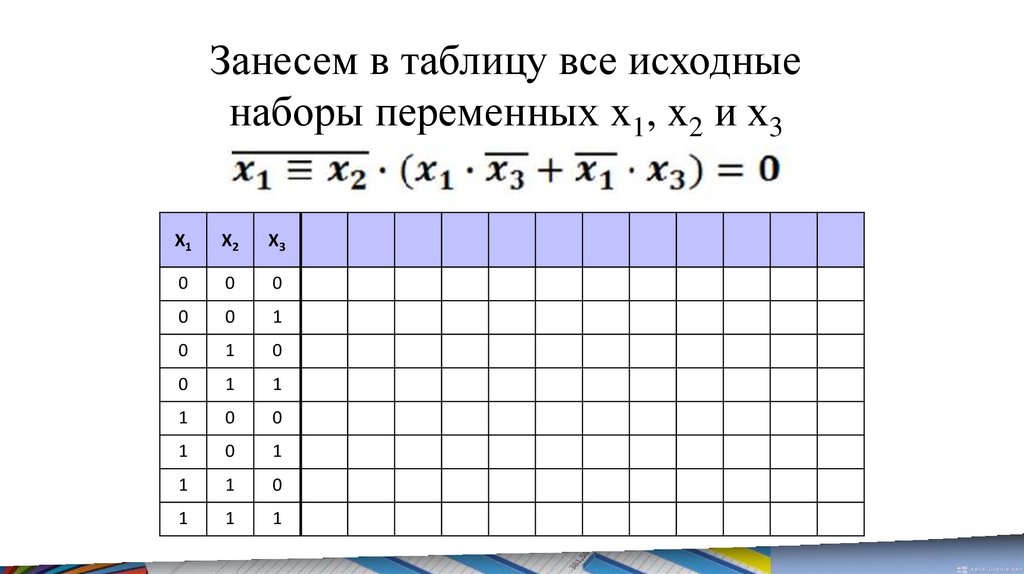
Занесем в таблицу все исходныенаборы переменных x1, x2 и x3
X1
X2
X3
0
0
0
0
0
1
0
1
0
0
1
1
1
0
0
1
0
1
1
1
0
1
1
1
9.
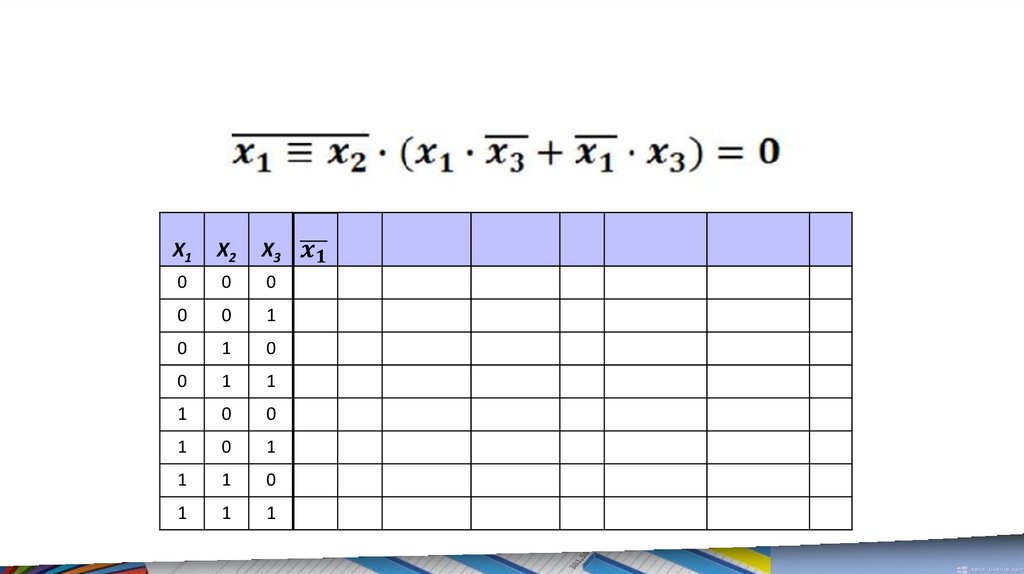
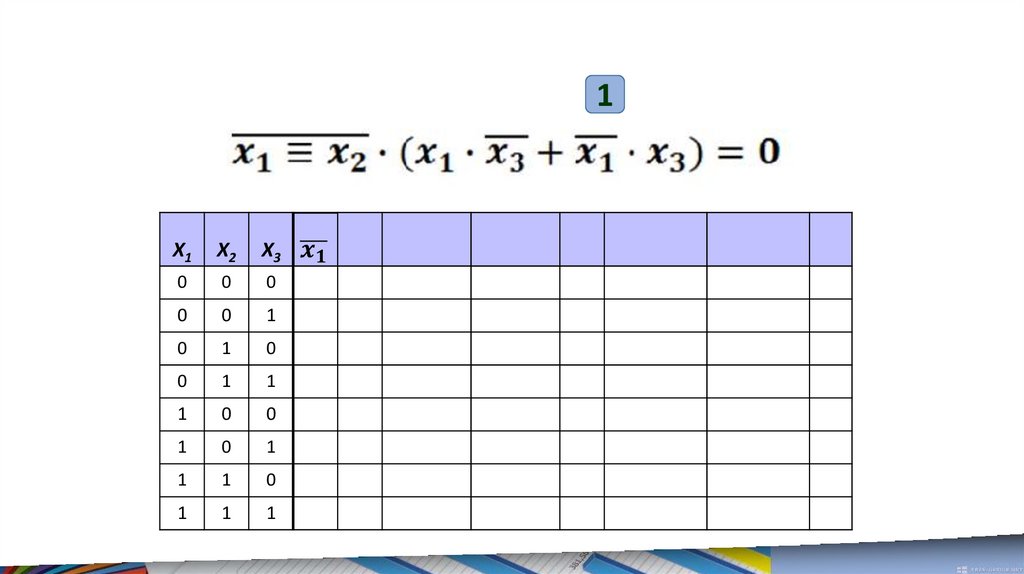
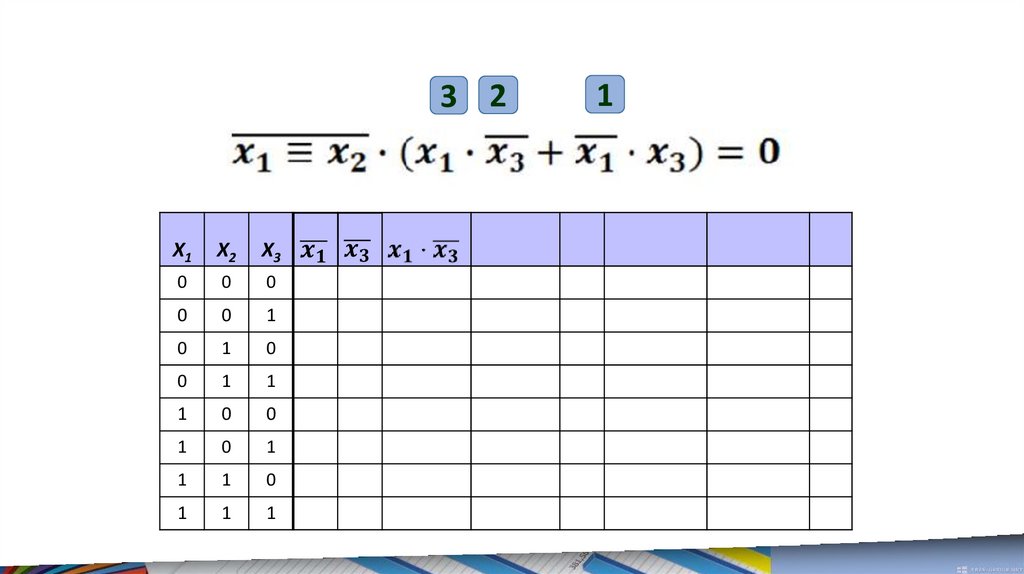
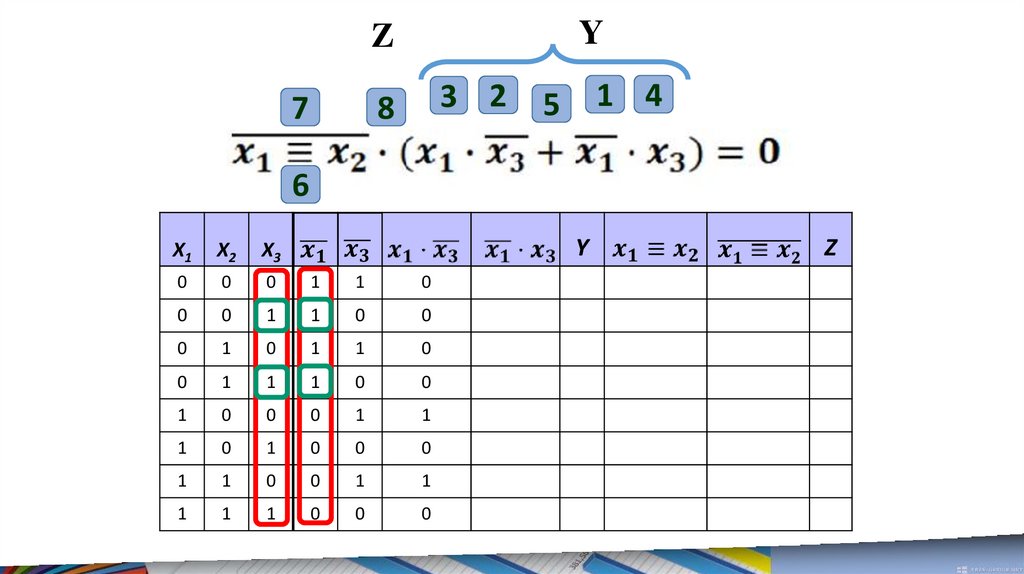
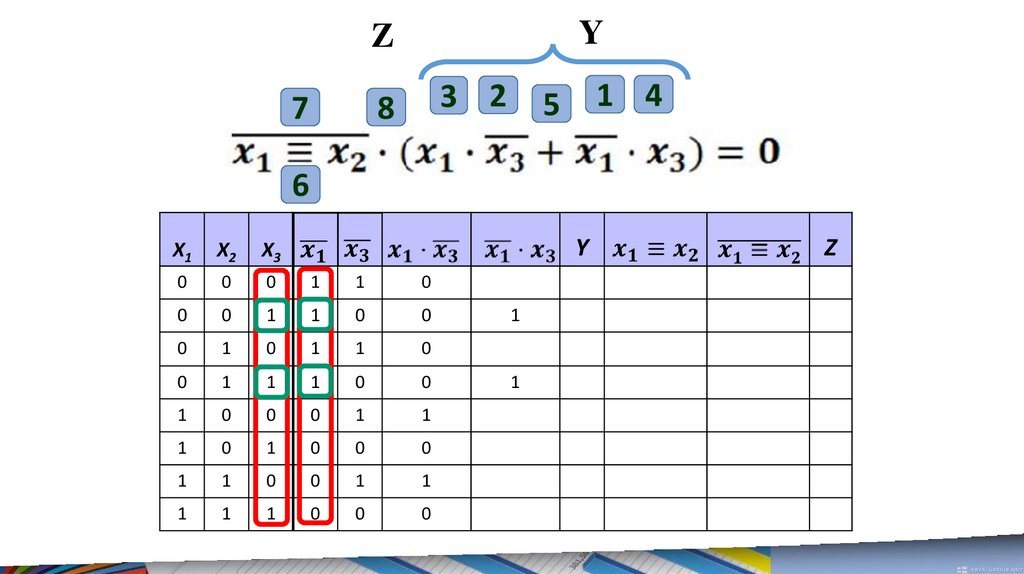
Расставим порядоквыполнения
логических
операций
1. Инверсия
2. Конъюнкция
3. Дизъюнкция
4. Импликация
5. Эквивалентность
10.
X1X2
X3
0
0
0
0
0
1
0
1
0
0
1
1
1
0
0
1
0
1
1
1
0
1
1
1
11.
1X1
X2
X3
0
0
0
0
0
1
0
1
0
0
1
1
1
0
0
1
0
1
1
1
0
1
1
1
12.
2X1
X2
X3
0
0
0
0
0
1
0
1
0
0
1
1
1
0
0
1
0
1
1
1
0
1
1
1
1
13.
3 2X1
X2
X3
0
0
0
0
0
1
0
1
0
0
1
1
1
0
0
1
0
1
1
1
0
1
1
1
1
14.
3 2X1
X2
X3
0
0
0
0
0
1
0
1
0
0
1
1
1
0
0
1
0
1
1
1
0
1
1
1
1 4
15.
3 2X1
X2
X3
0
0
0
0
0
1
0
1
0
0
1
1
1
0
0
1
0
1
1
1
0
1
1
1
5
1 4
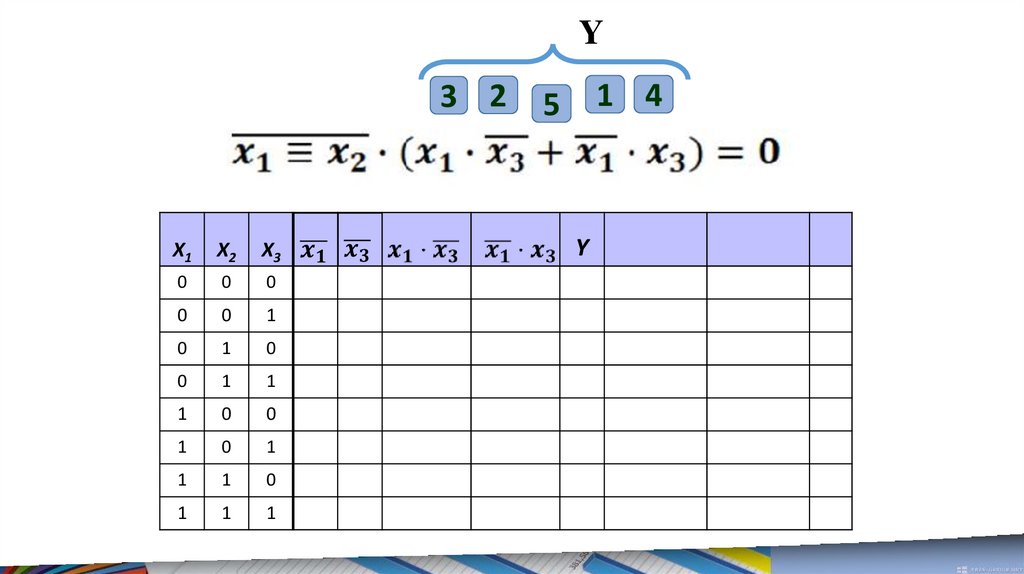
16.
Y3 2
X1
X2
X3
0
0
0
0
0
1
0
1
0
0
1
1
1
0
0
1
0
1
1
1
0
1
1
1
1 4
5
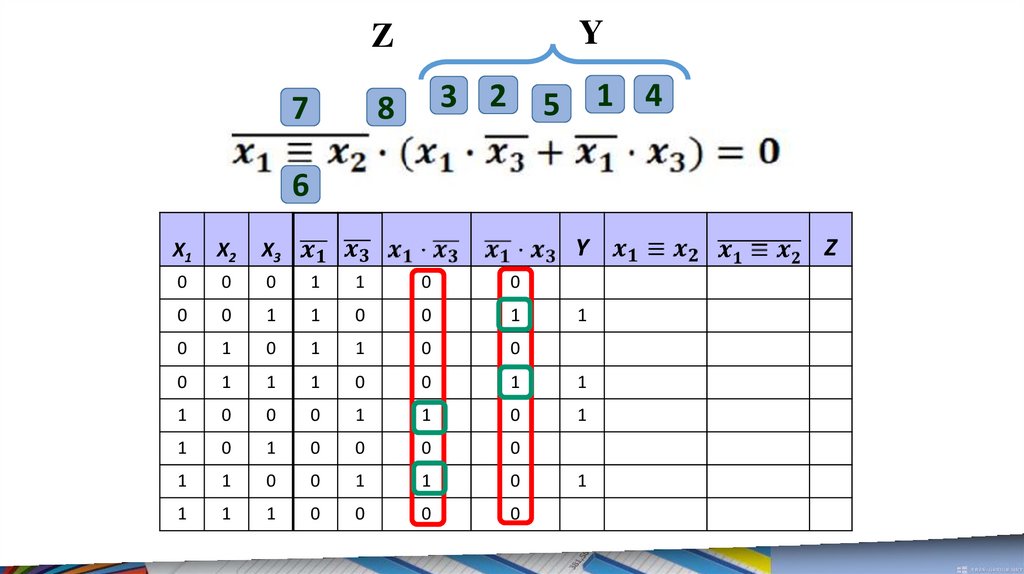
Y
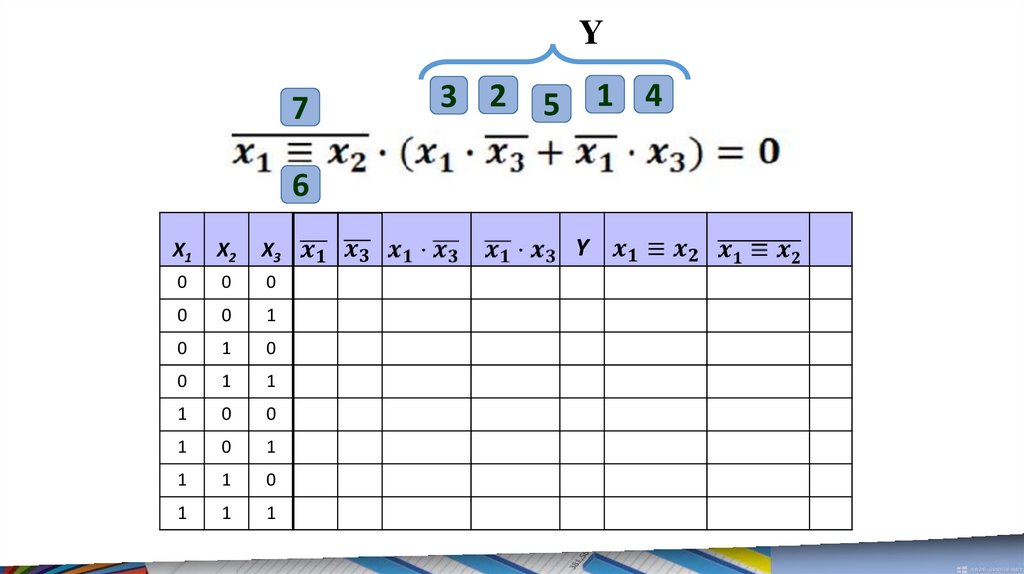
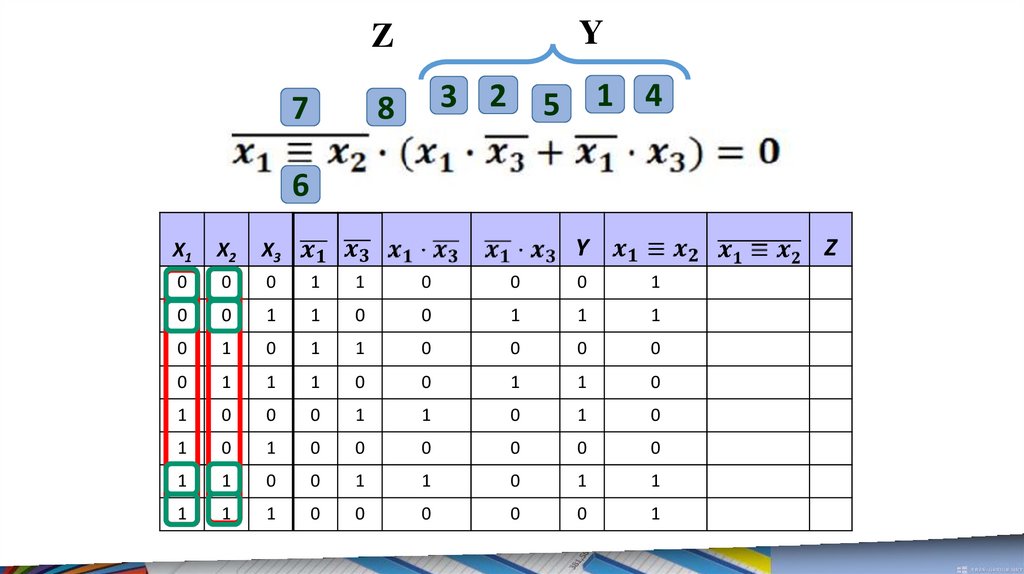
17.
Y3 2
1 4
5
6
X1
X2
X3
0
0
0
0
0
1
0
1
0
0
1
1
1
0
0
1
0
1
1
1
0
1
1
1
Y
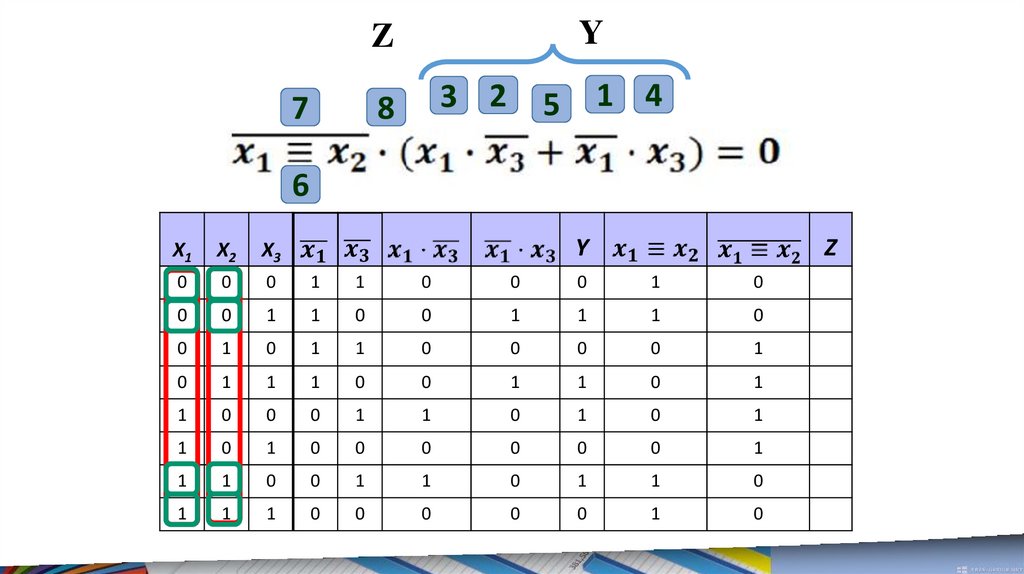
18.
Y7
3 2
1 4
5
6
X1
X2
X3
0
0
0
0
0
1
0
1
0
0
1
1
1
0
0
1
0
1
1
1
0
1
1
1
Y
19.
Y7
8
3 2
1 4
5
6
X1
X2
X3
0
0
0
0
0
1
0
1
0
0
1
1
1
0
0
1
0
1
1
1
0
1
1
1
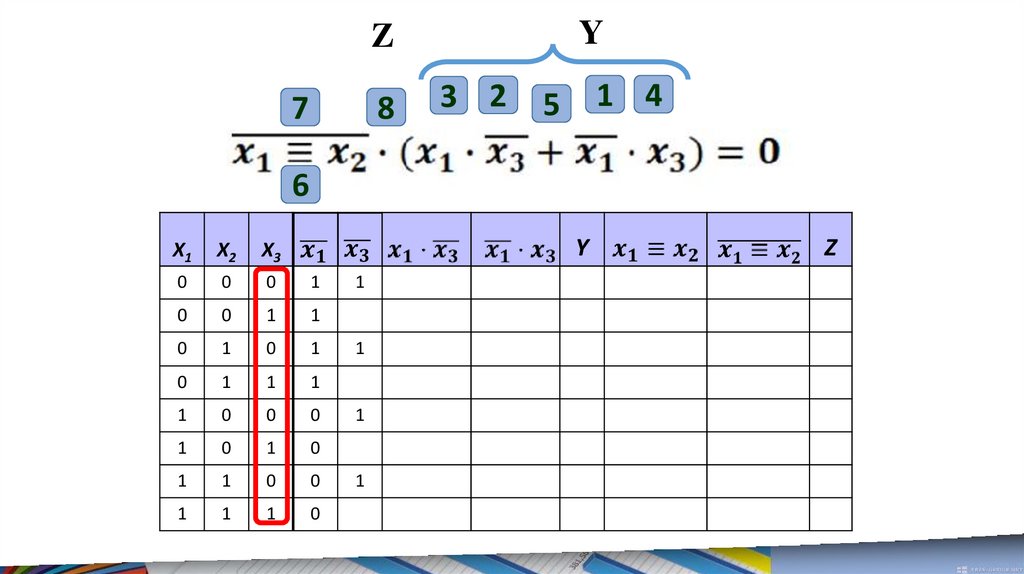
Y
Z
20.
YZ
7
8
3 2
1 4
5
6
X1
X2
X3
0
0
0
0
0
1
0
1
0
0
1
1
1
0
0
1
0
1
1
1
0
1
1
1
Y
Z
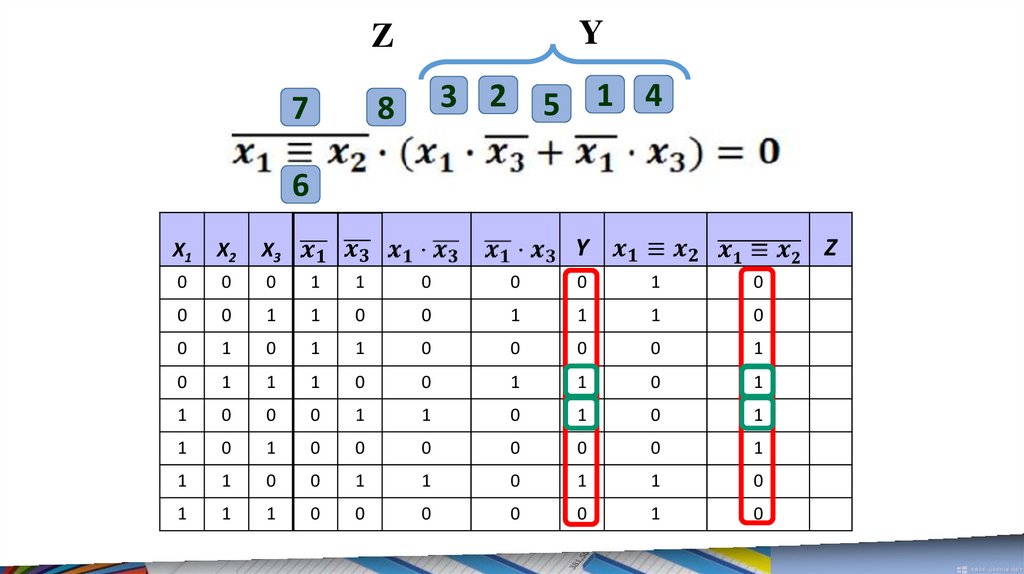
21.
YZ
7
8
3 2
1 4
5
6
Y
X1
X2
X3
0
0
0
1
0
0
1
1
0
1
0
1
0
1
1
1
1
0
0
1
0
1
1
1
0
1
1
1
Z
22.
YZ
7
8
3 2
1 4
5
6
Y
X1
X2
X3
0
0
0
1
0
0
1
1
0
1
0
1
0
1
1
1
1
0
0
0
1
0
1
0
1
1
0
0
1
1
1
0
Z
23.
YZ
7
8
3 2
1 4
5
6
Y
X1
X2
X3
0
0
0
1
0
0
1
1
0
1
0
1
0
1
1
1
1
0
0
0
1
0
1
0
1
1
0
0
1
1
1
0
1
1
1
1
Z
24.
YZ
7
8
3 2
1 4
5
6
Y
X1
X2
X3
0
0
0
1
1
0
0
1
1
0
0
1
0
1
1
0
1
1
1
0
1
0
0
0
1
1
0
1
0
0
1
1
0
0
1
1
1
1
0
0
Z
25.
YZ
7
8
3 2
1 4
5
6
Y
X1
X2
X3
0
0
0
1
1
0
0
1
1
0
0
1
0
1
1
0
1
1
1
0
1
0
0
0
1
1
0
1
0
0
1
1
0
0
1
1
1
1
0
0
Z
26.
YZ
7
8
3 2
1 4
5
6
Y
X1
X2
X3
0
0
0
1
1
0
0
1
1
0
0
1
0
1
1
0
1
1
1
0
1
0
0
0
1
1
0
1
0
0
1
1
0
0
1
1
1
1
0
0
Z
27.
YZ
7
8
3 2
1 4
5
6
Y
X1
X2
X3
0
0
0
1
1
0
0
1
1
0
0
1
0
1
1
0
1
1
1
0
1
0
0
0
1
1
0
1
0
0
1
1
0
0
1
1
1
1
0
0
Z
28.
YZ
7
3 2
8
1 4
5
6
Y
X1
X2
X3
0
0
0
1
1
0
0
1
1
0
0
1
0
1
1
0
1
1
1
0
1
0
0
0
1
1
0
1
0
0
1
1
0
0
1
1
1
1
0
0
1
1
Z
29.
YZ
7
3 2
8
1 4
5
6
Y
X1
X2
X3
0
0
0
1
1
0
0
0
1
1
0
0
0
1
0
1
1
0
0
1
1
1
0
0
1
0
0
0
1
1
1
0
1
0
0
0
1
1
0
0
1
1
1
1
1
0
0
0
Z
30.
YZ
7
3 2
8
1 4
5
6
Y
X1
X2
X3
0
0
0
1
1
0
0
0
1
1
0
0
0
1
0
1
1
0
0
1
1
1
0
0
1
0
0
0
1
1
1
0
1
0
0
0
1
1
0
0
1
1
1
1
1
0
0
0
Z
31.
YZ
7
3 2
8
1 4
5
6
Y
X1
X2
X3
0
0
0
1
1
0
0
0
1
1
0
0
0
1
0
1
1
0
0
1
1
1
0
0
1
0
0
0
1
1
1
0
1
0
0
0
1
1
0
0
1
1
1
1
1
0
0
0
Z
32.
YZ
7
3 2
8
1 4
5
6
Y
X1
X2
X3
0
0
0
1
1
0
0
0
1
1
0
0
0
1
0
1
1
0
0
1
1
1
0
0
1
0
0
0
1
1
1
0
1
0
0
0
1
1
0
0
1
1
1
1
1
0
0
0
1
1
Z
33.
YZ
7
3 2
8
1 4
5
6
Y
X1
X2
X3
0
0
0
1
1
0
0
0
0
1
1
0
0
1
0
1
0
1
1
0
0
0
1
1
1
0
0
1
1
0
0
0
1
1
0
1
0
1
0
0
0
0
1
1
0
0
1
1
0
1
1
1
0
0
0
0
Z
34.
YZ
7
3 2
8
1 4
5
6
Y
X1
X2
X3
0
0
0
1
1
0
0
0
0
1
1
0
0
1
0
1
0
1
1
0
0
0
1
1
1
0
0
1
1
0
0
0
1
1
0
1
0
1
0
0
0
0
1
1
0
0
1
1
0
1
1
1
0
0
0
0
Z
35.
YZ
7
3 2
8
1 4
5
6
Y
X1
X2
X3
0
0
0
1
1
0
0
0
0
1
1
0
0
1
0
1
0
1
1
0
0
0
1
1
1
0
0
1
1
0
0
0
1
1
0
1
0
1
0
0
0
0
1
1
0
0
1
1
0
1
1
1
0
0
0
0
Z
36.
YZ
7
3 2
8
1 4
5
6
Y
X1
X2
X3
0
0
0
1
1
0
0
0
0
1
1
0
0
1
0
1
0
1
1
0
0
0
1
1
1
0
0
1
1
1
0
0
0
1
1
0
1
1
0
1
0
0
0
0
1
1
0
0
1
1
0
1
1
1
0
0
0
0
1
1
Z
37.
YZ
7
3 2
8
1 4
5
6
Y
X1
X2
X3
0
0
0
1
1
0
0
0
0
0
1
1
0
0
1
1
0
1
0
1
1
0
0
0
0
1
1
1
0
0
1
1
1
0
0
0
1
1
0
1
1
0
1
0
0
0
0
0
1
1
0
0
1
1
0
1
1
1
1
0
0
0
0
0
Z
38.
YZ
7
3 2
8
1 4
5
6
Y
X1
X2
X3
0
0
0
1
1
0
0
0
0
0
1
1
0
0
1
1
0
1
0
1
1
0
0
0
0
1
1
1
0
0
1
1
1
0
0
0
1
1
0
1
1
0
1
0
0
0
0
0
1
1
0
0
1
1
0
1
1
1
1
0
0
0
0
0
Z
39.
YZ
7
3 2
8
1 4
5
6
Y
X1
X2
X3
0
0
0
1
1
0
0
0
0
0
1
1
0
0
1
1
0
1
0
1
1
0
0
0
0
1
1
1
0
0
1
1
1
0
0
0
1
1
0
1
1
0
1
0
0
0
0
0
1
1
0
0
1
1
0
1
1
1
1
0
0
0
0
0
Z
40.
YZ
7
3 2
8
1 4
5
6
Y
Z
X1
X2
X3
0
0
0
1
1
0
0
0
1
0
0
1
1
0
0
1
1
1
0
1
0
1
1
0
0
0
0
1
1
1
0
0
1
1
1
0
0
0
1
1
0
1
1
0
1
0
0
0
0
0
1
1
0
0
1
1
0
1
1
1
1
1
0
0
0
0
0
1
41.
YZ
7
3 2
8
1 4
5
6
Y
Z
X1
X2
X3
0
0
0
1
1
0
0
0
1
0
0
1
1
0
0
1
1
1
0
1
0
1
1
0
0
0
0
0
1
1
1
0
0
1
1
0
1
0
0
0
1
1
0
1
0
1
0
1
0
0
0
0
0
0
1
1
0
0
1
1
0
1
1
1
1
1
0
0
0
0
0
1
42.
YZ
7
3 2
8
1 4
5
6
Y
Z
X1
X2
X3
0
0
0
1
1
0
0
0
1
0
0
0
1
1
0
0
1
1
1
0
0
1
0
1
1
0
0
0
0
1
0
1
1
1
0
0
1
1
0
1
1
0
0
0
1
1
0
1
0
1
1
0
1
0
0
0
0
0
0
1
1
1
0
0
1
1
0
1
1
0
1
1
1
0
0
0
0
0
1
0
43.
YZ
7
3 2
8
1 4
5
6
Y
Z
X1
X2
X3
0
0
0
1
1
0
0
0
1
0
0
0
1
1
0
0
1
1
1
0
0
1
0
1
1
0
0
0
0
1
0
1
1
1
0
0
1
1
0
1
1
0
0
0
1
1
0
1
0
1
1
0
1
0
0
0
0
0
0
1
1
1
0
0
1
1
0
1
1
0
1
1
1
0
0
0
0
0
1
0
44.
YZ
7
3 2
8
1 4
5
6
Y
Z
X1
X2
X3
0
0
0
1
1
0
0
0
1
0
0
0
1
1
0
0
1
1
1
0
0
1
0
1
1
0
0
0
0
1
0
1
1
1
0
0
1
1
0
1
1
0
0
0
1
1
0
1
0
1
1
0
1
0
0
0
0
0
0
1
1
1
0
0
1
1
0
1
1
0
1
1
1
0
0
0
0
0
1
0
45.
YZ
7
3 2
8
1 4
5
6
Y
Z
X1
X2
X3
0
0
0
1
1
0
0
0
1
0
0
0
1
1
0
0
1
1
1
0
0
1
0
1
1
0
0
0
0
1
0
1
1
1
0
0
1
1
0
1
1
1
0
0
0
1
1
0
1
0
1
1
1
0
1
0
0
0
0
0
0
1
1
1
0
0
1
1
0
1
1
0
1
1
1
0
0
0
0
0
1
0
46.
YZ
7
3 2
8
1 4
5
6
Y
Z
X1
X2
X3
0
0
0
1
1
0
0
0
1
0
0
0
0
1
1
0
0
1
1
1
0
0
0
1
0
1
1
0
0
0
0
1
0
0
1
1
1
0
0
1
1
0
1
1
1
0
0
0
1
1
0
1
0
1
1
1
0
1
0
0
0
0
0
0
1
0
1
1
0
0
1
1
0
1
1
0
0
1
1
1
0
0
0
0
0
1
0
0
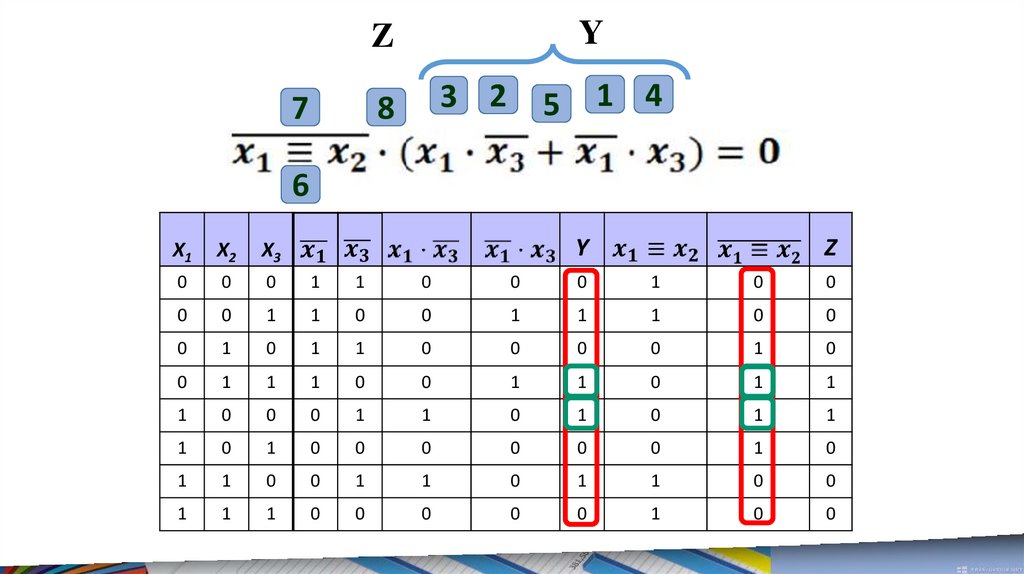
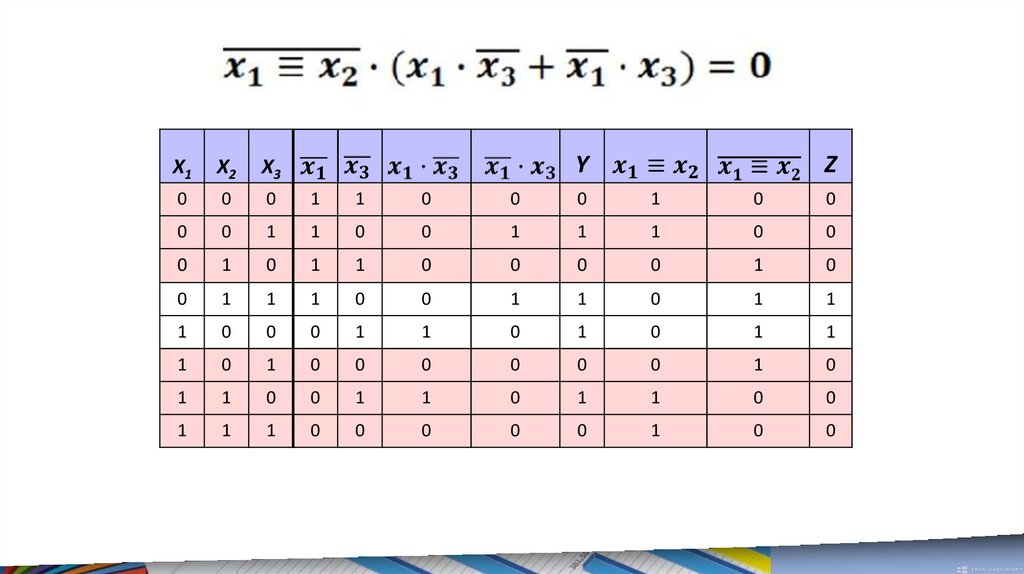
47.
YZ
X1
X2
X3
0
0
0
1
1
0
0
0
1
0
0
0
0
1
1
0
0
1
1
1
0
0
0
1
0
1
1
0
0
0
0
1
0
0
1
1
1
0
0
1
1
0
1
1
1
0
0
0
1
1
0
1
0
1
1
1
0
1
0
0
0
0
0
0
1
0
1
1
0
0
1
1
0
1
1
0
0
1
1
1
0
0
0
0
0
1
0
0
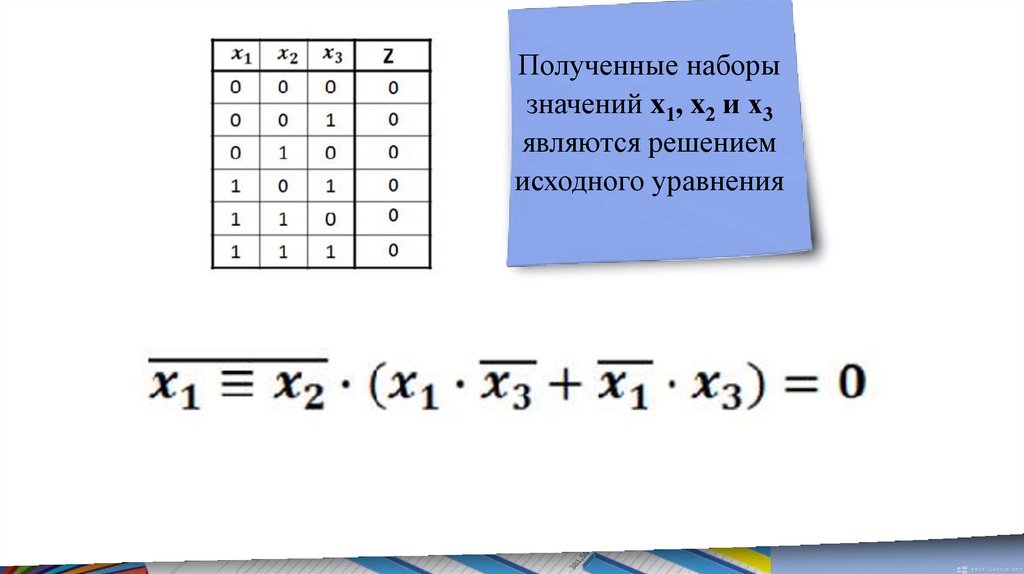
48.
Полученные наборызначений x1, x2 и x3
являются решением
исходного уравнения
49.
Паре 00 соответствуют пары 00 и 01X1 X2
00
01
10
11
X2 X3
00
01
10
11
50.
Паре 11 соответствуют пары 10 и 11X1 X2
00
01
10
11
X2 X3
00
01
10
11
51.
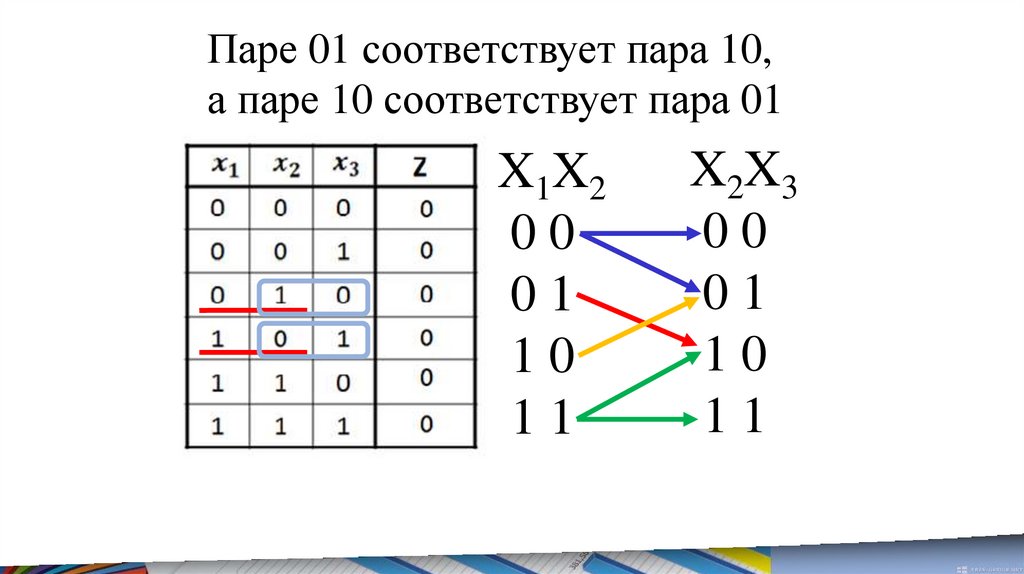
Паре 01 соответствует пара 10,а паре 10 соответствует пара 01
X1 X2
00
01
10
11
X2 X3
00
01
10
11
52.
53.
54.
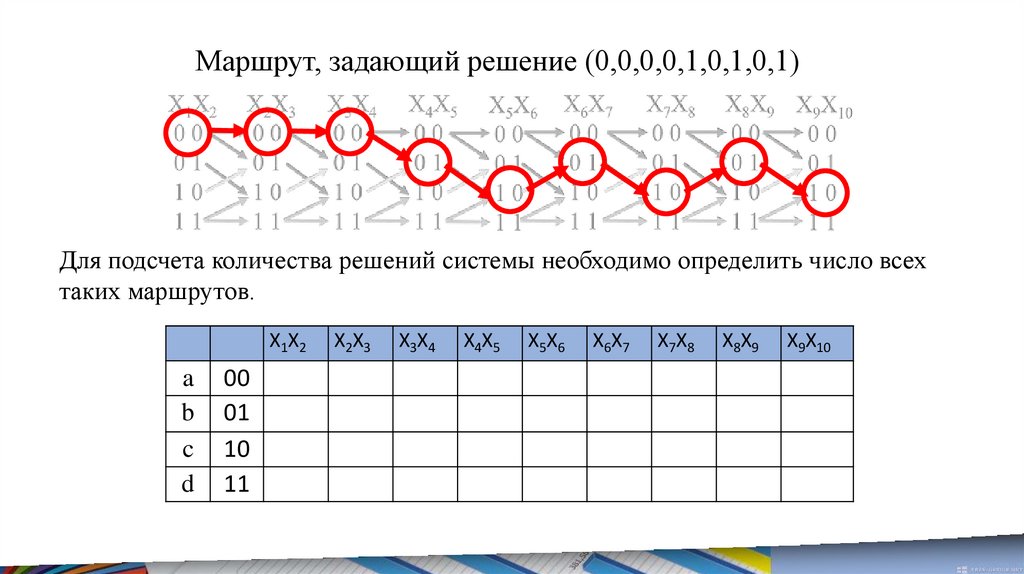
Маршрут, задающий решение (0,0,0,0,1,0,1,0,1)Для подсчета количества решений системы необходимо определить число всех
таких маршрутов.
X1X2
a
b
c
d
00
01
10
11
X2X3
X3X4
X4X5
X5X6
X6X7
X7X8
X8X9
X9X10
55.
X1X2a
b
c
d
00
01
10
11
1
1
1
1
X2X3
X3X4
X4X5
X5X6
X6X7
X7X8
X8X9
X9X10
56.
X1X2a
b
c
d
00
01
10
11
X2X3
X3X4
X4X5
X5X6
X6X7
X7X8
X8X9
X9X10
1
1
1
1
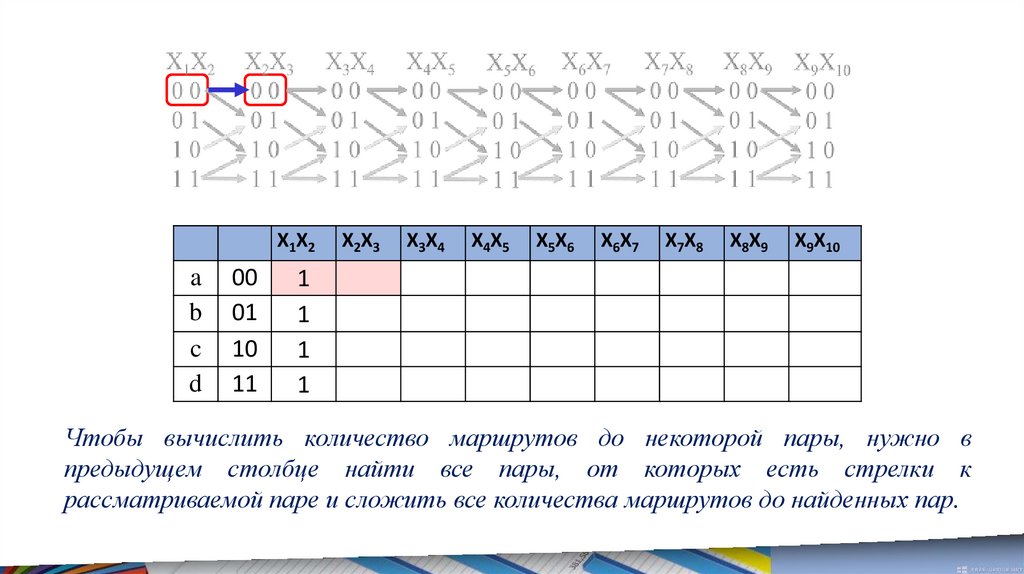
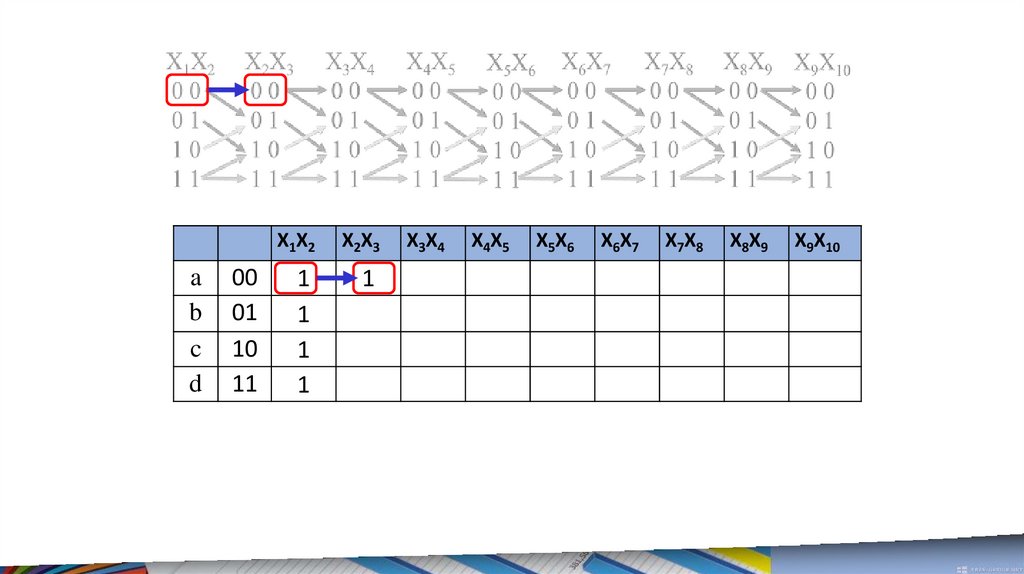
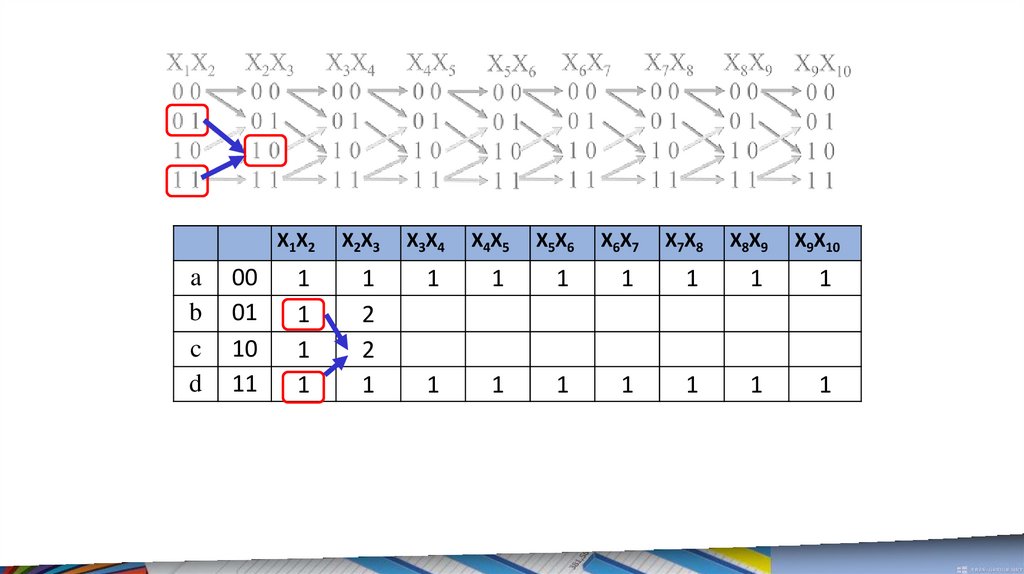
Чтобы вычислить количество маршрутов до некоторой пары, нужно в
предыдущем столбце найти все пары, от которых есть стрелки к
рассматриваемой паре и сложить все количества маршрутов до найденных пар.
57.
ab
c
d
00
01
10
11
X1X2
X2X3
1
1
1
1
1
X3X4
X4X5
X5X6
X6X7
X7X8
X8X9
X9X10
58.
ab
c
d
00
01
10
11
X1X2
X2X3
X3X4
X4X5
X5X6
X6X7
X7X8
X8X9
1
1
1
1
1
1
1
1
1
1
1
X9X10
1
59.
ab
c
d
00
01
10
11
X1X2
X2X3
X3X4
X4X5
X5X6
X6X7
X7X8
X8X9
X9X10
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
60.
X1X2a
b
c
d
00
01
10
11
1
1
1
1
X2X3
X3X4
X4X5
X5X6
X6X7
X7X8
X8X9
X9X10
1
1+1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
61.
ab
c
d
00
01
10
11
X1X2
X2X3
X3X4
X4X5
X5X6
X6X7
X7X8
X8X9
X9X10
1
1
1
1
1
2
2
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
62.
ab
c
d
00
01
10
11
X1X2
X2X3
1
1
1
1
1
2
2
1
X3X4
X4X5
X5X6
X6X7
X7X8
X8X9
X9X10
1
1+2
1
1
1
1
1
1
1
1
1
1
1
1
1
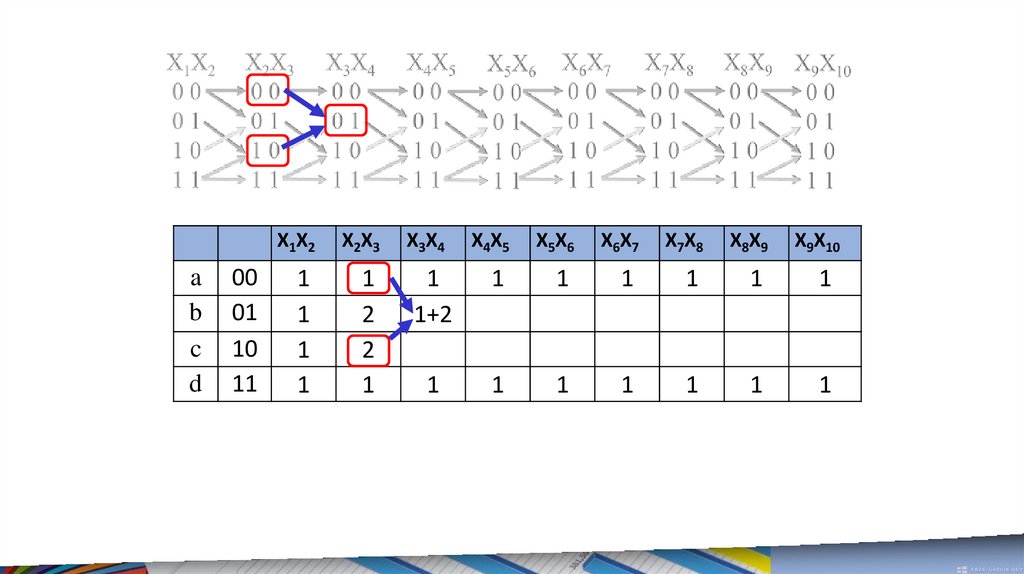
63.
ab
c
d
00
01
10
11
X1X2
X2X3
X3X4
X4X5
X5X6
X6X7
X7X8
X8X9
X9X10
1
1
1
1
1
2
2
1
1
3
1
1
1
1
1
1
1
1
1
1
1
1
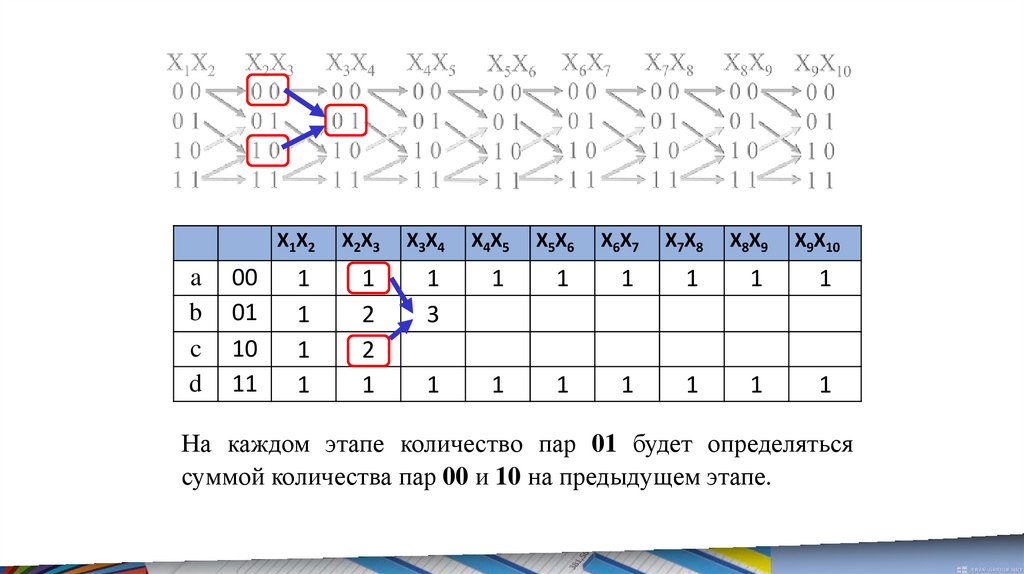
1
На каждом этапе количество пар 01 будет определяться
суммой количества пар 00 и 10 на предыдущем этапе.
64.
Пусть F() - этофункция,
вычисляющая
количество пар на
следующем шаге
Составим
формулы
F (00) = F (00)
F (01) = F (00) + F (10)
F (10) = F (01) + F (11)
F (11) = F (11)
65.
Пусть F() - этофункция,
вычисляющая
количество пар на
следующем шаге
a
b
c
d
Упростим
66.
F (00) = F (00)F (01) = F (00) + F (10)
F (10) = F (01) + F (11)
F (11) = F (11)
a
b
c
d
00
01
10
11
a
a+c
b+d
d
a
b
c
d
X1X2
X2X3
X3X4
X4X5
X5X6
X6X7
X7X8
X8X9
X9X10
1
1
1
1
1
2
2
1
1
3
1
1
1
1
1
1
1
1
1
1
1
1
1
67.
F (00) = F (00)F (01) = F (00) + F (10)
F (10) = F (01) + F (11)
F (11) = F (11)
a
b
c
d
00
01
10
11
a
a+c
b+d
d
a
b
c
d
X1X2
X2X3
X3X4
X4X5
X5X6
X6X7
X7X8
X8X9
X9X10
1
1
1
1
1
2
2
1
1
3
3
1
1
1
1
1
1
1
1
1
1
1
1
1
68.
F (00) = F (00)F (01) = F (00) + F (10)
F (10) = F (01) + F (11)
F (11) = F (11)
a
b
c
d
00
01
10
11
a
a+c
b+d
d
a
b
c
d
X1X2
X2X3
X3X4
X4X5
X5X6
X6X7
X7X8
X8X9
X9X10
1
1
1
1
1
2
2
1
1
3
3
1
1
4
1
1
1
1
1
1
1
1
1
1
1
69.
F (00) = F (00)F (01) = F (00) + F (10)
F (10) = F (01) + F (11)
F (11) = F (11)
a
b
c
d
00
01
10
11
a
a+c
b+d
d
a
b
c
d
X1X2
X2X3
X3X4
X4X5
X5X6
X6X7
X7X8
X8X9
X9X10
1
1
1
1
1
2
2
1
1
3
3
1
1
4
4
1
1
1
1
1
1
1
1
1
1
1
70.
F (00) = F (00)F (01) = F (00) + F (10)
F (10) = F (01) + F (11)
F (11) = F (11)
a
b
c
d
00
01
10
11
a
a+c
b+d
d
a
b
c
d
X1X2
X2X3
X3X4
X4X5
X5X6
X6X7
X7X8
X8X9
X9X10
1
1
1
1
1
2
2
1
1
3
3
1
1
4
4
1
1
5
1
1
1
1
1
1
1
1
1
71.
F (00) = F (00)F (01) = F (00) + F (10)
F (10) = F (01) + F (11)
F (11) = F (11)
a
b
c
d
00
01
10
11
a
a+c
b+d
d
a
b
c
d
X1X2
X2X3
X3X4
X4X5
X5X6
X6X7
X7X8
X8X9
X9X10
1
1
1
1
1
2
2
1
1
3
3
1
1
4
4
1
1
5
5
1
1
1
1
1
1
1
1
1
72.
F (00) = F (00)F (01) = F (00) + F (10)
F (10) = F (01) + F (11)
F (11) = F (11)
a
b
c
d
00
01
10
11
a
a+c
b+d
d
a
b
c
d
X1X2
X2X3
X3X4
X4X5
X5X6
X6X7
X7X8
X8X9
1
1
1
1
1
2
2
1
1
3
3
1
1
4
4
1
1
5
5
1
1
6
6
1
1
7
7
1
1
8
8
1
X9X10
1
9
9
1
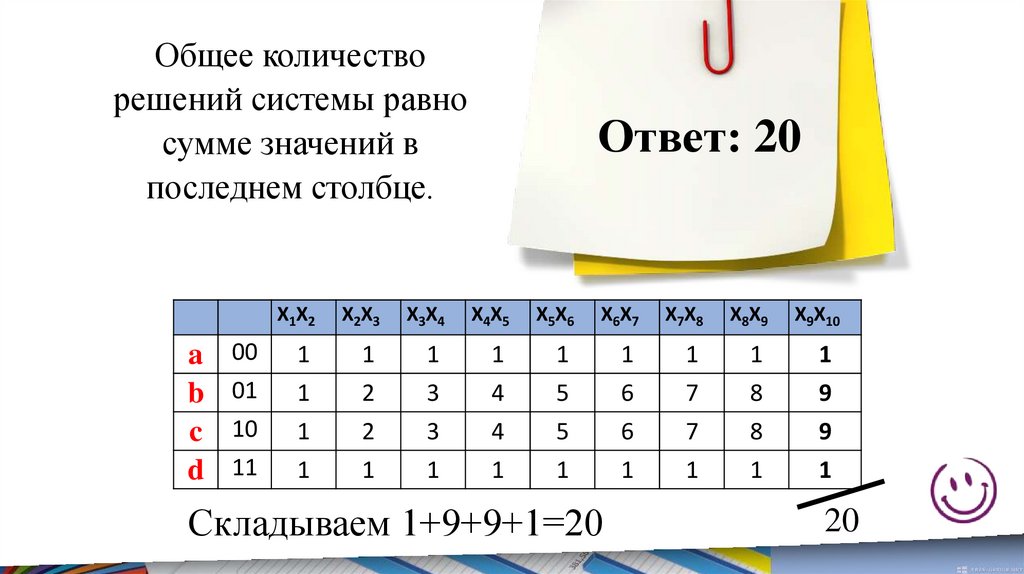
73.
Общее количестворешений системы равно
сумме значений в
последнем столбце.
a
b
c
d
00
01
10
11
Ответ: 20
X1X2
X2X3
X3X4
X4X5
X5X6
X6X7
X7X8
X8X9
1
1
1
1
1
2
2
1
1
3
3
1
1
4
4
1
1
5
5
1
1
6
6
1
1
7
7
1
1
8
8
1
Складываем 1+9+9+1=20
X9X10
1
9
9
1
20









































 mathematics
mathematics








