Similar presentations:
Финансовая математика. Кредиты
1.
Финансовая математикаКредиты
2.
Виды экономических задач(профильный уровень)
1) Вклады
2) Кредиты
3) Оптимизация
3.
В задачах по теме «Кредит» используют три основных видаплатежа:
1. Дифференцированные платежи (ежемесячные или
ежегодные платежи, уменьшающиеся к концу срока
кредитования и обеспечивающие уменьшение суммы долга
на одну и ту же величину)
2. Аннуитетные платежи (постоянные ежемесячные или
ежегодные платежи, которые не меняются на протяжении
всего периода кредитования, но долг изменяется не
равномерно)
3. Фиксированные платежи (платежи, которые чѐтко
оговариваются в условии задачи)
4.
Дифференцированные платежи(ежемесячные или ежегодные платежи, уменьшающиеся к концу срока
кредитования и обеспечивающие уменьшение суммы долга на одну и ту же
величину)
Ключевые фразы:
• долг должен быть на X тысяч рублей меньше долга на n-е
число предыдущего месяца;
• n-го числа каждого месяца долг должен быть на одну и ту
же сумму меньше долга на n-е число предыдущего месяца.
Формула переплаты
П- переплата
S- сумма кредита
r- процентная ставка
n- промежуток времени
r n 1
П
S
100 2
5.
Дифференцированные платежи (платежи, уменьшающиесяк концу срока, уменьшение суммы долга на одну и ту же величину)
S=20млн, n=5, r=25%, П-?
Период
Долг
%
Сумма
выплат
Остаток
1
4
20∙0,25=5
9
16
2
4
16∙0,25=4
8
12
3
4
12∙0,25=3
7
8
4
4
8∙0,25=2
6
4
5
4
4∙0,25=1
5
0
Итого
20
15
35
r n 1
П
S
100 2
25 5 1
1 6 20
П
20
15
100 2
4 2
6.
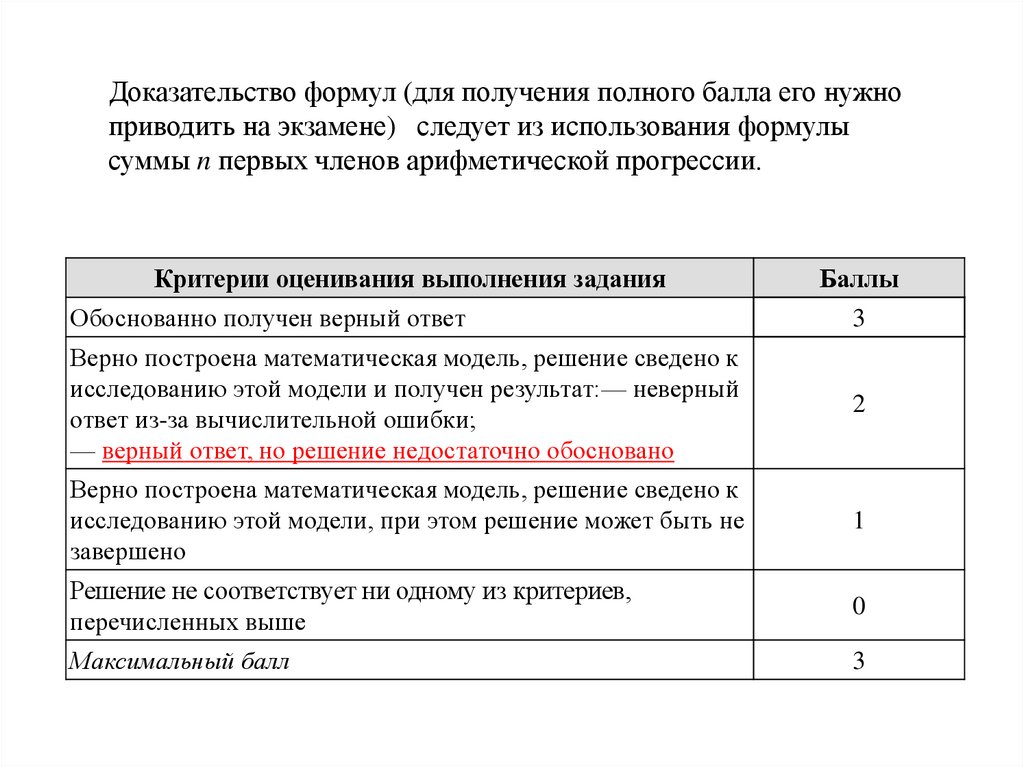
Доказательство формул (для получения полного балла его нужноприводить на экзамене) следует из использования формулы
суммы n первых членов арифметической прогрессии.
Критерии оценивания выполнения задания
Баллы
Обоснованно получен верный ответ
3
Верно построена математическая модель, решение сведено к
исследованию этой модели и получен результат:— неверный
ответ из-за вычислительной ошибки;
— верный ответ, но решение недостаточно обосновано
2
Верно построена математическая модель, решение сведено к
исследованию этой модели, при этом решение может быть не
завершено
1
Решение не соответствует ни одному из критериев,
перечисленных выше
0
Максимальный балл
3
7.
Кристина и Карина увидели в магазине губную помаду редкого зеленогоцвета стоимостью 5000 рублей.
Чтобы купить помаду, Кристина в тот же день взяла в микрокредитной
организации кредит на 5000 рублей под 1% в день сроком на 1 год (365
дней), причем ежедневные платежи по кредиту списывались с
банковского счета Кристины и подбирались так, чтобы сумма долга
уменьшалась равномерно.
Сколько заплатит Кристина за помаду редкого зеленого цвета?
S=5000, n=365, r=1%, Sn-?
r n 1
П
S
100 2
1 365 1
1 366 5000
П
5000
183 50 9150( руб )
100
2
100 2
5000 9150 14150( руб )
Sn
Ответ : 14150 руб.
8.
В июле планируется взять кредит в банке на сумму 16 млн рублей на некоторыйсрок (целое число лет). Условия его возврата таковы:
— каждый январь долг возрастает на 25% по сравнению с концом предыдущего
года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же сумму меньше долга на
июль предыдущего года.
На сколько лет планируется взять кредит, если известно, что общая сумма выплат
после его полного погашения составит 38 млн рублей?
S=16,
r=25%,
Sn=38,
n-?
П=38-16=22
r n 1
П
S
100 2
25 n 1
22
16
100 2
(n 1) 16
22
4 2
22 (n 1) 2
n 1 11
Ответ: 10 лет
n 10
9.
15-го января планируется взять кредит в банке на 19 месяцев. Условияего возврата таковы:
— 1-го числа каждого месяца долг возрастёт на r% по сравнению с
концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть
долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же сумму
меньше долга на 15-е число предыдущего месяца. Известно, что общая
сумма выплат после полного погашения кредита на 30% больше суммы,
взятой в кредит. Найдите r.
r n 1
n=19, r=?,
Sn=1,3S,
П=0,3S
Ответ: 3%
П
100
S
2
r 19 1
0,3S
S
100
2
3S
r 20 S
10
100 2
3
r
10 10
r 3
10.
15-го января планируется взять кредит в банке на 18 месяцев. Условия еговозврата таковы:
— 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом
предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же величину
меньше долга на 15-е число предыдущего месяца.
Сколько процентов от суммы кредита составляет общая сумма денег, которую
нужно выплатить банку за весь срок кредитования?
n=18, r=2%,
Sn=xS, х-?, П-?
r n 1
П
S
100 2
2 18 1
2 19 S
П
S
0,19 S
100
2
100 2
S n S 0,19S 1,19S
Ответ: 119%
11.
Аннуитетные платежи(платежи одинаковые, но долг изменяется не равномерно)
Ключевые фразы:
• известно, что кредит был выплачен тремя равными
платежами (за 3 года);
• он будет платить каждый год по 2 073 600 рублей;
• кредит можно выплатить за четыре года равными
платежами по 56 507 рублей.
12.
Карина тоже купила зеленую помаду, в этот же день взяв кредит на сумму5000 рублей. Схема выплаты кредита следующая: 1 числа каждого
следующего месяца банк начисляет 50% на оставшуюся сумму долга, и
затем Карина переводит в банк очередной платеж. Известно, что Карина
выплатила кредит двумя равными платежами.
1 апреля
1 мая
1 июня
Долг
5000
Остаток
5000+2500=7500или
5000•1,5=7500
(7500-х)•1,5
7500-х
(7500-х)•1,5-х=0
11250-1,5х-х=0
11250-2,5х=0
х=4500
4500+4500=9000(руб)
Ответ:9 000 руб (Кристина заплатила 14 150 руб)
13.
Аннуитетные платежи(платежи одинаковые, но долг изменяется не равномерно)
x- размер одного платежа, S- сумма кредита
r- процентная ставка, k=1+0,01r
1 год
2 год
3 год
4 год
Долг
Sk
Остаток
Sk-х
(Sk-x)•k=Sk²-xk
(Sk²-xk-x)•k=
Skᶾ-xk²-xk
Sk²-xk-x= Sk²-x(k+1)
Sk³-xk²-xk-x=
Sk³-x(k²+k+1)
4
S k -x(k³+k²+k+1)
14.
В июле 2020 года планируется взятькредит в банке на некоторую сумму.
Условия его возврата таковы:
каждый
январь
долг
увеличивается на 25 по сравнению
с концом предыдущего года;
- с февраля по июнь каждого года
необходимо
выплатить
одним
платежом часть долга.
Сколько рублей будет выплачено
банку, если известно, что кредит
будет полностью погашен тремя
равными платежами (то есть за три
года) и общая сумма выплат после
полного погашения кредита на
104800 рублей больше суммы, взятой
в кредит?
n=3, Sn-S=104800, r=25%,
k=1,25=1¼,
5
S n 3 x, k 4
3 x S 104800
Sk 3 x(k 2 k 1) 0
125
25 5
S
x( 1) 0
64
16 4
125
61
S
x
64
16
S 125
x
244
125S
3x S 3
S 104800
244
375 244
S(
) 104800
244
S 195200
S n 195200 104800 300000
15.
В июле 2020 года планируется взять кредит на некоторую сумму. Условиявозврата таковы:
— в январе каждого года долг увеличивается на 13% по сравнению с
предыдущим годом;
— с февраля по июнь нужно выплатить часть долга одним платежом.
Определите, на какую сумму взяли кредита банке, если известно, что
кредит был выплачен двумя равными платежами, равными 5 107 600
рублей.
n=2, х=5 107 600, r=13%, k=1,13, S-?
Sk 2 x(k 1) 0
Sk 2 x(k 1)
x(k 1)
k2
5107600 (1,13 1) 5107600 213 100
S
400 213 100 8520000
1,2769
12769
Ответ : 8520000 рублей
S
16.
В июле планируется взять кредит на сумму 8052000 рублей. Условия его возврататаковы:
- каждый январь долг возрастает на 20% по сравнению с концом предыдущего
года;
- с февраля по июнь каждого года необходимо выплатить некоторую часть долга.
Сколько рублей нужно платить ежегодно, чтобы кредит был полностью погашен
четырьмя равными платежами (то есть за 4 года)?
n=4, S=8 052 000, х-?, r=20%, k=1,2,
6
Sk 4 x(k 3 k 2 k 1 0, k
5
Sk 4 x(k 3 k 2 k 1) x(k 2 1)(k 1)
Sk 4
x 2
(k 1)(k 1)
6 4
64
8052000 ( )
8052000 4
8052000 6 4 5 8052000 6 4
5
5
x
2400 6 4
4
6
6
36 25 6 5
5 11 61
11 61 5
(( ) 2 1)( 1)
5
5
25
5
2400 1296 3110400
Ответ : 3110400 рублей
17.
Анатолий решил взять кредит в банке 331000 рублей на 3 месяцапод 10% в месяц. Существуют две схемы выплаты кредита.
По первой схеме банк в конце каждого месяца начисляет проценты
на оставшуюся сумму долга (то есть увеличивает долг на 10%),
затем Анатолий переводит в банк фиксированную сумму и в
результате выплачивает весь долг тремя равными платежами
(аннуитетные платежи).
По второй схеме тоже сумма долга в конце каждого месяца
увеличивается на 10%, а затем уменьшается на сумму, уплаченную
Анатолием. Суммы, выплачиваемые в конце каждого месяца,
подбираются так, чтобы в результате сумма долга каждый месяц
уменьшалась равномерно, то есть на одну и ту же величину
(дифференцированные платежи). Какую схему выгоднее выбрать
Анатолию? Сколько рублей будет составлять эта выгода?
18.
По первой схеме банк в конце каждого месяца начисляет проценты наоставшуюся сумму долга (то есть увеличивает долг на 10%), затем
Анатолий переводит в банк фиксированную сумму и в результате
выплачивает весь долг тремя равными платежами (аннуитетные
платежи).
n=3,
S=331 000,
х-?,
r=10%,
k=1,1,
Sk 3 x( k 2 k 1) 0
Sk 3 x( k 2 k 1)
11 3
121 11
331000 ( ) x(
1)
10
100 10
121 110 100
331 1331 x (
)
100
331
331 1331 x
100
x
1331
100
x 133100
S n 133100 3 399300
19.
По второй схеме тоже сумма долга в конце каждого месяца увеличиваетсяна 10%, а затем уменьшается на сумму, уплаченную Анатолием. Суммы,
выплачиваемые в конце каждого месяца, подбираются так, чтобы в
результате сумма долга каждый месяц уменьшалась равномерно, то есть
на одну и ту же величину (дифференцированные платежи). Какую схему
выгоднее выбрать Анатолию? Сколько рублей будет составлять эта
выгода?
n=3, S=331 000, х-?, r=10%, k=1,1
r n 1
П
S
100 2
10 3 1
1 2 331000
П
331000
66200
100 2
10
S n 331000 66200 397200
Более выгодно выбрать вторую схему, выгода составит
399 300-397 200=2 100(руб)
Ответ: 2100 рублей
20.
Фиксированные платежи(долг уменьшается по заданным в таблице или в условии
задачи параметрам)
Ключевые фразы:
• выплатили за 2 года платежами 130 000 рублей в
первый год и 150 000 рублей во второй
• 15-го числа каждого месяца долг должен
составлять некоторую сумму в соответствии со
следующей таблицей
21.
31 декабря 2020 года Борис взял вбанке 1 млн. рублей в кредит. Схема
выплаты кредита следующая:
-31 декабря каждого следующего
года банк начисляет проценты на
оставшуюся сумму долга ( то есть
увеличивает долг на определенное
количество процентов), затем Борис
переводит очередной транш.
Борис выплатил кредит за два
транша, переводя в первый раз 560
тыс. рублей, во второй – 661,1 тыс.
рублей. Под какой процент банк
выдал кредит Борису?
S= 1000 тыс. руб.
X1=560 тыс. руб.
X2=644,1 тыс. руб. r-?
k 1 0,01r
( Sk x1 )k x 2 0
Sk 2 kx1 x 2 0
1000k 2 560k 644,1 0
D 560 2 4 1000 644,1 2890000
560 1700
1,13
2 1000
k2 0
k1
k 1,13
r 0,13 13%
Ответ : 13%
22.
15-го января планируется взять кредит в банке на шесть месяцев вразмере 1 млн рублей. Условия его возврата таковы:
— 1-го числа каждого месяца долг увеличивается на r процентов по
сравнению с концом предыдущего месяца, где r — целое число;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть
долга;
— 15-го числа каждого месяца долг должен составлять некоторую
сумму в соответствии со следующей таблицей.
Найдите наибольшее значение r, при котором общая сумма выплат
будет меньше 1,2 млн рублей.
Дата
15.01
15.02
15.03
15.04
15.05
15.06
15.07
Долг
(в млн
рублей)
1
0,6
0,4
0,3
0,2
0,1
0
23.
Дата15.01
15.02
15.03
15.04
15.05
15.06
15.07
Долг
(в млн
рублей)
1
0,6
0,4
0,3
0,2
0,1
0
S=1 млн., n=6, r -?, Sn<1,2 млн.
r
П
(1 0,6 0,4 0,3 0,2 0,1)
П<0,2
100
r
П
2,6 0,2
100
0,2 100
r
2,6
9
r 7
13
r 7
24.
В июле 2016 года планируется взять кредит в банке на три года вразмере S млн рублей, где S — целое число. Условия его возврата таковы:
− каждый январь долг увеличивается на 20% по сравнению с концом
предыдущего года;
− с февраля по июнь каждого года необходимо выплатить одним
платежом часть долга;
− в июле каждого года долг должен составлять часть кредита в
соответствии со следующей таблицей
Найдите наименьшее значение S, при котором каждая из выплат будет
меньше 5 млн рублей.
Месяц и год
Долг(в млн
рублей)
Июль 2016
Июль 2017
Июль 2018
Июль 2019
S
0,8S
0,4S
0
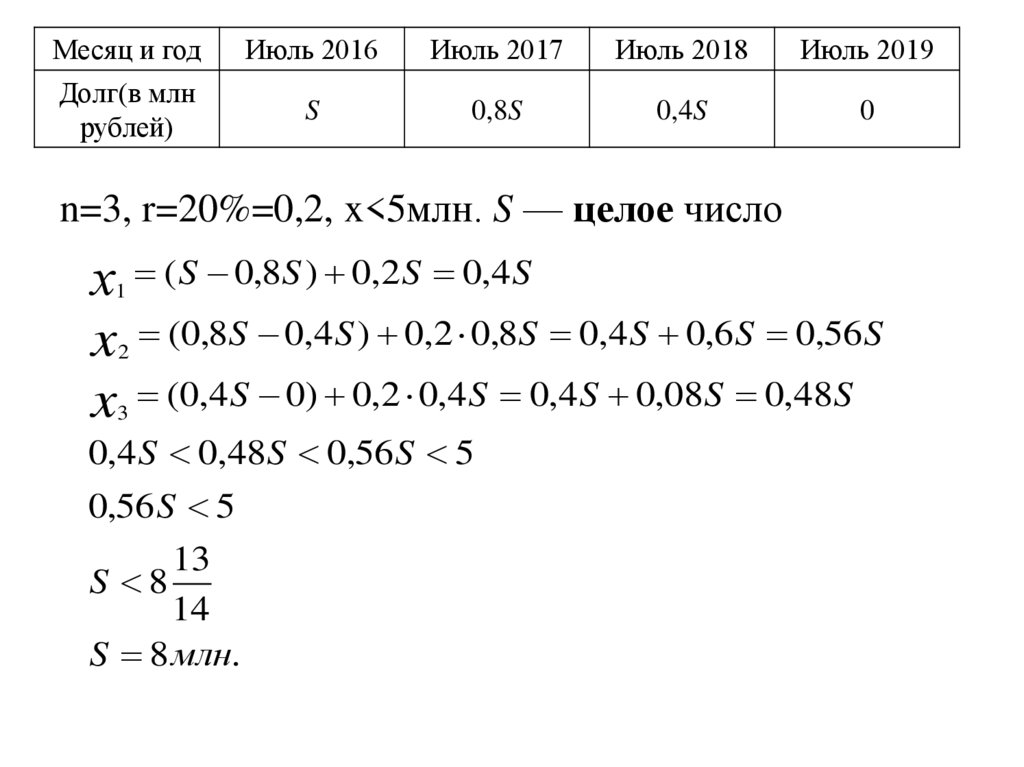
25.
Месяц и годДолг(в млн
рублей)
Июль 2016
Июль 2017
Июль 2018
Июль 2019
S
0,8S
0,4S
0
n=3, r=20%=0,2, x<5млн. S — целое число
х
x
x
1
2
3
( S 0,8S ) 0,2 S 0,4 S
(0,8S 0,4 S ) 0,2 0,8S 0,4 S 0,6 S 0,56 S
(0,4 S 0) 0,2 0,4 S 0,4 S 0,08S 0,48S
0,4 S 0,48S 0,56 S 5
0,56 S 5
13
S 8
14
S 8 млн.
26.
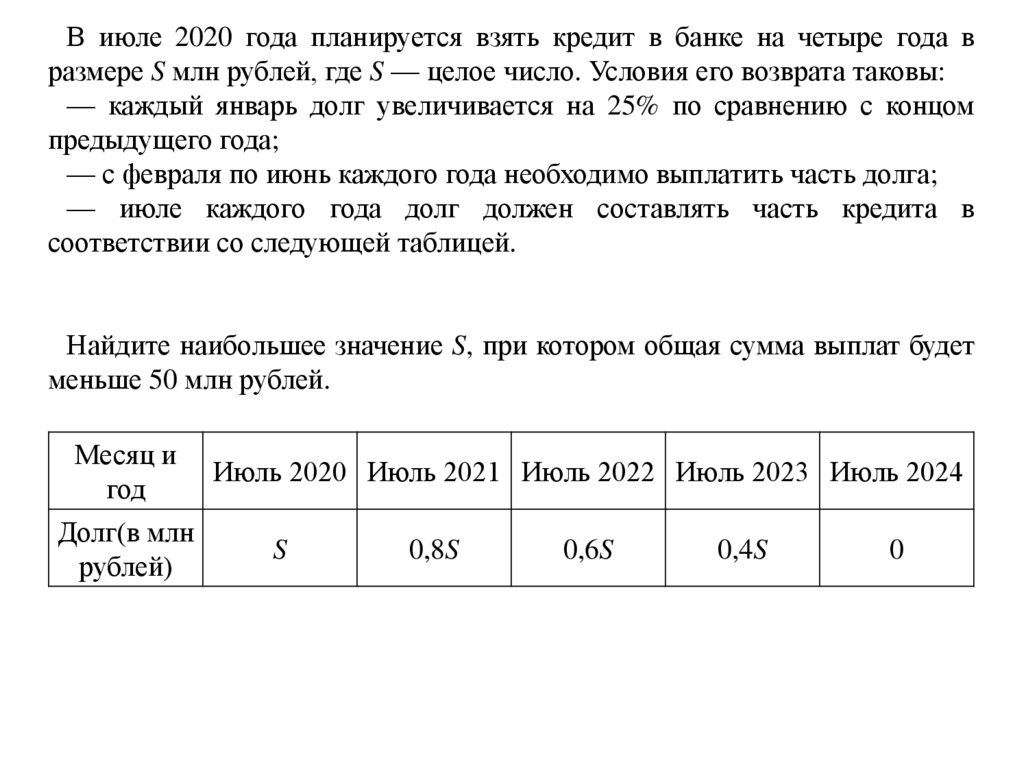
В июле 2020 года планируется взять кредит в банке на четыре года вразмере S млн рублей, где S — целое число. Условия его возврата таковы:
— каждый январь долг увеличивается на 25% по сравнению с концом
предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— июле каждого года долг должен составлять часть кредита в
соответствии со следующей таблицей.
Найдите наибольшее значение S, при котором общая сумма выплат будет
меньше 50 млн рублей.
Месяц и
Июль 2020 Июль 2021 Июль 2022 Июль 2023 Июль 2024
год
Долг(в млн
S
0,8S
0,6S
0,4S
0
рублей)
27.
Месяц иИюль 2020 Июль 2021 Июль 2022 Июль 2023 Июль 2024
год
Долг(в млн
S
0,8S
0,6S
0,4S
0
рублей)
n=4, r=25%=0,25=1/4, S-целое, Sn<50млн.
25
(1S 0,8S 0,6 S 0,4 S )
П
100
1
П 2,8 0,7 S
4
S n S 0,7 S 1,7 S
1,7 S 50
7
S 29
17
S 29 млн.
28.
В июле 2019 года планируется взять кредит в банке на три года вразмере S млн рублей, где S — целое число. Условия его возврата таковы:
− каждый январь долг увеличивается на 25% по сравнению с концом
предыдущего года;
− с февраля по июнь каждого года необходимо выплатить одним
платежом часть долга;
− в июле каждого года долг должен составлять часть кредита в
соответствии со следующей таблицей
Найдите наименьшее значение S, при котором разница между
наибольшим и наименьшим платежом меньше 1 млн рублей.
Месяц и год
Долг(в млн
рублей)
Июль 2019
Июль 2020
Июль 2021
Июль 2022
S
0,7S
0,4S
0
29.
Месяц и годДолг(в млн
рублей)
Июль 2019
Июль 2020
Июль 2021
Июль 2022
S
0,7S
0,4S
0
n=3, r=25%=0,25=1/4, Xmax- Xmin<1млн.
х
x
x
x
1
2
3
( S 0,7 S ) 0,25S 0,55S
(0,7 S 0,4 S ) 0,25 0,7 S 0,3S 0,175S 0,475S
(0,4 S 0) 0,25 0,4 S 0,4 S 0,1S 0,5S
max
0,55S , xmin 0,475S
0,55S 0,475S 1
0,075S 1
1
S 13
3
S 13 млн.


























 mathematics
mathematics finance
finance








