Финансовая математика в задачах ГИА. Алгоритмы решения задач на банковские вклады, кредиты и проценты

1.

Финансовая математика в
задачах ГИА: алгоритмы
решения задач на банковские
вклады, кредиты и проценты.

2.

Проценты
Процент – это сотая часть величины или числа.
Перевод дроби в проценты: чтобы перевести обыкновенную
дробь в проценты, нужно сначала перевести её в десятичную
дробь, а потом умножить на 100 и добавить знак %.
Представление процентов десятичными дробями: чтобы
проценты перевести в число, нужно убрать знак % и разделить
число на 100.

3.

Чтобы высчитать какой-либо процент от числа, следует само
число разделить на 100, а полученный результат умножить на
количество процентов. (чтобы найти a% от b, надо b*0,01a)
Чтобы найти число по его указанному проценту, нужно заданное
число разделить на указанную величину процента, а результат
умножить на 100. (Если известно, что a% числа х равно b, то х=b: 0,01а)
Чтобы найти процентное отношение чисел, надо отношение этих
чисел умножить на 100%.
Отношение двух чисел – это частное от деления одного из них на
другое.
Пропорция – это верное равенство двух отношений.
В пропорции a:b =c:d числа a и d называют крайними, а числа b и
c – средними членами пропорции.
Основное свойство пропорции: произведение крайних членов
пропорции равно произведению её средних членов.

4.

Примеры решения заданий из открытого
банка заданий для подготовки к ГИА
Пример 1. Тетрадь стоит 24 рубля. Сколько рублей заплатит
покупатель за 60 тетрадей, если при покупке больше 50 тетрадей
магазин делает скидку 10% от стоимости всей покупки?
Решение. За 60 тетрадей покупатель заплатил бы
60 · 24 = 1440 рублей.
Скидка составит 10%, т. е. 10% = 0,1, 1440 · 0,1 = 144 рубля.
Значит, покупатель заплатит
1440 − 144 = 1296 рублей.
Ответ: 1296.

5.

Пример 2. Футболка стоила 800 рублей. После снижения цены
она стала стоить 680 рублей. На сколько процентов была снижена
цена на футболку?
Решение. Цена на футболку была снижена на
800 − 680 = 120 рублей.
Разделим 120 на 800:
120 : 800 = 0,15
Значит, цена на футболку была снижена на 15%.
Ответ: 15.

6.

Пример 3. В школе французский язык изучают 124 учащихся, что
составляет 25% от числа всех учащихся школы. Сколько учащихся в
школе?
Решение. Запишем проценты в виде десятичной дроби:
25 % = 25 :100 = 0,25.
Разделим 124 на 0,25:
124 : 0,25 = 496.
Значит, в школе учится 496 учеников.
Ответ: 496.

7.

Пример 4. В городе N живет 200 000 жителей. Среди них 15%
детей и подростков. Среди взрослых жителей 45% не работает
(пенсионеры, студенты, домохозяйки и т.п.). Сколько взрослых
жителей работает?
Решение. Найдем сначала численность взрослого населения. В
городе 15% детей и подростков, значит, 100-15=85% взрослого
населения. Запишем проценты десятичной дробью:
85 : 100 = 0,85.
200000 · 0,85 = 170000 человек взрослого населения.
Среди них 45% не работающих, то есть работающих
100-45=55% , 55% = 55 : 100 = 0,55.
Значит, 170000 · 0,55 = 93500 взрослых жителей работает.
Ответ: 93500.

8.

Пример 5. Налог на доходы составляет 13% от заработной платы.
После удержания налога на доходы Мария Константиновна получила
9570 рублей. Сколько рублей составляет заработная платы Марии
Константиновны?
Решение. Пусть заработная плата Марии Константиновны
составляет x рублей. Тогда:
x − 0,13x = 9570;
0,87x = 9570;
x = 9570 : 0,87;
x = 11 000.
Значит, зарплата Марии Константиновны составляет 11 000 рублей.
Ответ: 11 000.

9.

Пример 6. В сентябре 1 кг винограда стоил 60 рублей, в октябре
виноград подорожал на 25%, а в ноябре еще на 20%. Сколько рублей
стоил 1 кг винограда после подорожания в ноябре?
Решение. В октябре виноград подорожал на 60 · 0,25 = 15 рублей
и стал стоить 60 + 15 = 75 рублей. В ноябре виноград подорожал на
75 · 0,2 = 15 рублей. Значит, после подорожания в ноябре 1 кг
винограда стоил 75 + 15 = 90 рублей.
Ответ: 90.

10.

Финансовая математика
Финансовая математика — раздел прикладной математики,
имеющий дело с математическими задачами, связанными
с финансовыми расчётами.
Объектом изучения являются любые финансово-кредитные
операции, которые предполагают наличие ряда условий, с которыми
согласны участвующие стороны. К таким условиям относятся:
• денежные суммы;
• временные параметры;
• процентные ставки и некоторые другие дополнительные величины.

11.

Схемы решения задач на кредиты
Первая схема: кредит погашается равными платежами. Или
известна информация о платежах.
Вторая схема: равномерно уменьшается сумма долга. Или дана
информация об изменении суммы долга.
В задачах первого типа обычно применяется формула для суммы
геометрической прогрессии. В задачах второго типа — формула суммы
арифметической прогрессии.
Схемы решения задач на кредиты отличаются друг от друга.
Поэтому
первое, что надо сделать, когда решаете
«экономическую» задачу на кредиты или вклады, — определить, к
какому типу она относится.

12.

Примеры решения заданий из открытого
банка заданий для подготовки к ГИА
Пример 1. 31 декабря 2014 года Алексей взял в банке 6 902 000
рублей в кредит под 12,5% годовых. Схема выплаты кредита
следующая — 31 декабря каждого следующего года банк начисляет
проценты на оставшуюся сумму долга (то есть увеличивает долг на
12,5%), затем Алексей переводит в банк X рублей. Какой должна быть
сумма X, чтобы Алексей выплатил долг четырьмя равными платежами
(то есть за четыре года)?
Это задача первого типа. Есть информация о платежах. В условии
сказано, что Алексей выплатит долг четырьмя равными платежами.

13.

Решение. Пусть сумма кредита равна S, а годовые составляют a %. Тогда 31
декабря каждого года оставшаяся сумма долга умножается на коэффициент b = 1 +
0,01a. После первой выплаты сумма долга составит S1 = Sb − x.
После второй выплаты сумма долга составит
S2 = S1b - x = (Sb - x)b - x = Sb2 - (1 + b)x.
После третьей выплаты сумма оставшегося долга равна
S3 = Sb3 - (1 + b +b2)x
После четвёртой выплаты сумма оставшегося долга равна
S4 = Sb4 - (1 + b +b2 +b3)x
По условию четырьмя выплатами Алексей должен погасить кредит полностью,
поэтому
Sb4 - (1 + b +b2 +b3)x = 0, откуда x = Sb4 : (1 + b +b2 +b3) .
При S = 6 902 000 и a = 12,5, получаем: b = 1,125 и
x = 2296350 (рублей)
Ответ: 2 296 350.

14.

Пример 2. Жанна взяла в банке в кредит 1,8 млн рублей на срок
24 месяца. По договору Жанна должна возвращать банку часть денег
в конце каждого месяца. Каждый месяц общая сумма долга
возрастает на 1 %, а затем уменьшается на сумму, уплаченную
Жанной банку в конце месяца. Суммы, выплачиваемые Жанной,
подбираются так, чтобы сумма долга уменьшалась равномерно, то
есть на одну и ту же величину каждый месяц. Какую сумму Жанна
вернёт банку в течение первого года кредитования?
В этой задаче сумма долга уменьшается равномерно — задача
второго типа.

15.

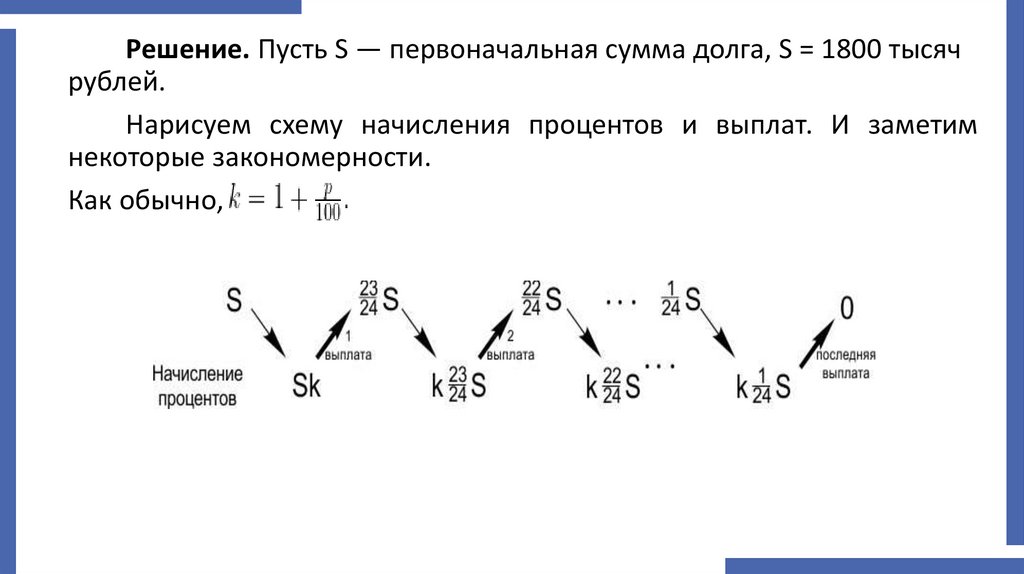
Решение. Пусть S — первоначальная сумма долга, S = 1800 тысяч
рублей.
Нарисуем схему начисления процентов и выплат. И заметим
некоторые закономерности.
Как обычно,

16.

Сумма долга уменьшается равномерно. Можно сказать —
равными ступеньками. И каждая ступенька равна
После первой выплаты сумма долга равна
после второй
Тогда первая выплата
вторая выплата ,
. ...
Последняя в году выплата
Сумма всех выплат в течение первого года:
В первой «скобке» — сумма 12 членов арифметической
прогрессии, в которой

17.

Обозначим эту сумму
Во второй скобке — также
арифметической прогрессии, в которой
Эту сумму обозначим
сумма
12
членов

18.

Общая сумма выплат за год:
тысяч рублей.
Ответ. 1066500 рублей.