Пропорции и отношения

1. Пропорции и отношения

2.

План учебного материала
• Отношения. Основное свойство отношений.
• Пропорция. Основное свойство пропорций.
• Решение уравнений на основе свойств
пропорции.
• Процентное отношение двух чисел. Процентные
расчеты. Задачи экономического содержания.
• Прямая пропорциональная зависимость.
• Задачи на пропорциональное деление .

3.

Отношения.
Основное
свойство
отношений.

4.

Отношения
Частное двух чисел
называют отношением этих чисел.
Отношение показывает,
во сколько раз одно число больше другого
или какую часть составляет одно число от другого.
3:5
43
54
2,7:0,4
3 4
:
7 8

5.

Отношения
частное
3:5
дробь
отношения
43
54

6.

Основное свойство
отношения
Отношение двух чисел не изменится,
если каждое из них умножить или разделить
на одно и то же число,
отличное от нуля.
Оба члена пропорции можно поделить
на их общий делитель.
Отношение дробных чисел можно заменить
отношением натуральных чисел.

7.

Пропорция.
Основное
свойство
пропорции.

8.

Пропорция
Равенство двух отношений
называют пропорцией.
a
c
a : b = c : d, или
b d
при b ≠ 0 і d ≠ 0
a, d – крайние члены пропорции
c, b – средние члены пропорции

9.

Основное свойство
пропорции
Произведение крайних членов каждой пропорции
равно произведению ёё средних членов.
Если a : b = c : d то a · d = c · b
4 : 2 = 8 : 4 то 4 · 4 = 8 · 2

10.

Неизвестный член
пропорции
Чтобы найти неизвестный крайний член пропорции,
достаточно произведение ёё средних членов
поделить на известный крайний.
Чтобы найти неизвестный средний член пропорции,
достаточно произведение ёё крайних членов поделить
на известный средний.

11.

Решение
уравнений
на основе
свойств
пропорции.

12.

Решите уравнение
x : 2 = 3 : 11
2 3 6
x
11 11

13.

Решите уравнение
0 ,5 0 ,15
x
2 ,4
0 ,5 2 ,4
x
0 ,15
5 24
8
15

14.

Решите уравнение
1
1
x :1 4 :
2
3
1
1
x 1 4 :
2
3
3 4 3
18
2 1

15.

Процентное
отношение
двух чисел.
Процентные расчёты.
Задачи экономического
содержания.

16.

Процентное отношение
Если отношение двух чисел выражают в процентах,
то его называют процентным отношением.
Один процент – это одна сотая часть
1% = 0,01
100% = 1
50% = 0,5
200% = 2

17.

Процентное отношение
Существует три основных вида задач на проценты
нахождение процентов от числа
нахождение числа по значению его процента
нахождение процентного отношения двух чисел

18.

Процентное отношение
Необходимо впахать поле, площадь которого равна 300 га.
В первый день трактористы выполнили 40% задания.
Сколько гектаров они вспахали за первый день?
складываем
пропорцию
40 %
S = 300 га
300 га – 100 %
х га – 40 %
находим неизвестный
член пропорции
300 100
,
x
40
300 40
x
120 га
100

19.

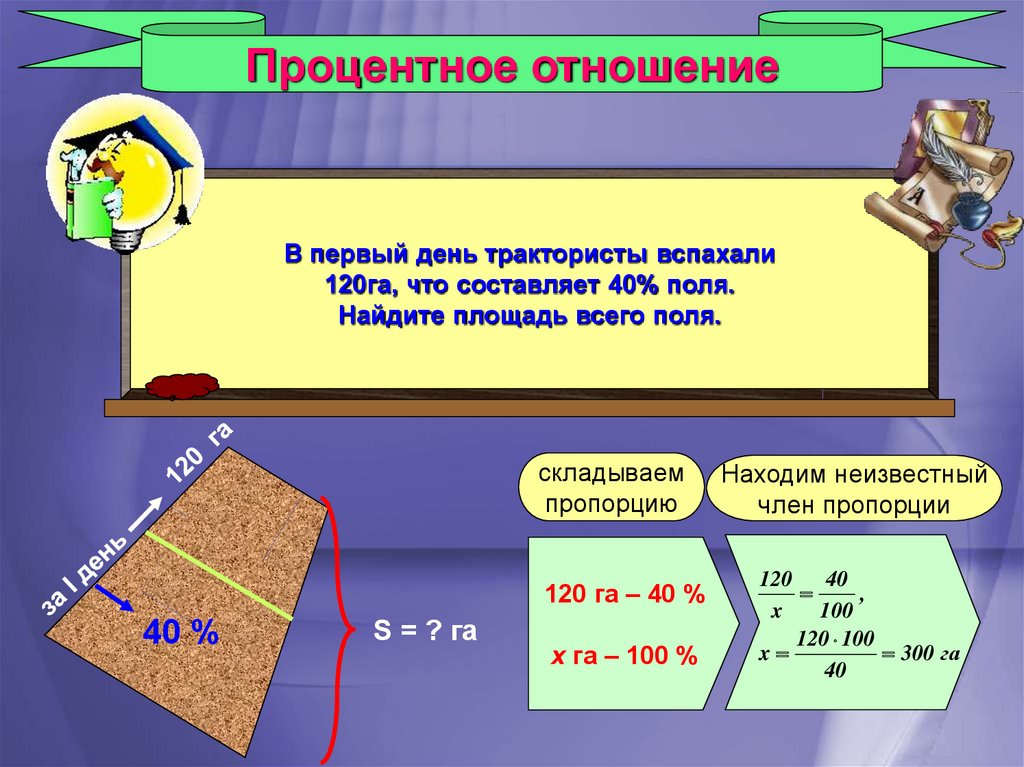
Процентное отношение
В первый день трактористы вспахали
120га, что составляет 40% поля.
Найдите площадь всего поля.
складываем
пропорцию
120 га – 40 %
40 %
S = ? га
х га – 100 %
Находим неизвестный
член пропорции
120 40
,
x
100
120 100
x
300 га
40

20.

Процентное отношение
Необходимо вспахать поле, площадь которого 300га.
В первый день трактористы вспахали 120 га.
Сколько процентов всего поля они вспахали в первый день?
складываем
пропорцию
300 га – 100 %
?%
S = 300 га
120 га – х %
Находим неизвестный
член пропорции
300 100
,
120
x
120 100
x
40 %
300

21.

Прямая
пропорциональная
зависимость.

22.

Прямая пропорциональная зависимость
Две величины называют прямо пропорциональными,
если с увеличением (уменьшением) значений
одной из них в несколько раз значение другой
увеличивается (уменьшается) во столько же раз.
Скорость, км/ч
60
60
60
60
Время, ч
1
2
3
4
Путь, км
60
120 180 240

23.

Обратно пропорциональная зависимость
Две величины называют обратно пропорциональными,
если с увеличением (уменьшением) значений
одной из них в несколько раз значения другой
уменьшаются (увеличиваются) во столько же раз.
Скорость, км/ч
50
60
Время, ч
6
5
Путь, км
100 150
4
3
300 300 300 300

24.

Задачи на
пропорциональное
деление.

25.

Задачи на пропорциональное деление
Чтобы поделить число на части, пропорциональные
данным числам, нужно поделить его на сумму
данных чисел и найденное частное умножить
на каждое из них.
Проволоку длиной 60 м разрезали на 3 части,
длины которых пропорциональны числам 2, 3 і 5.
Найдите длины этих частей проволоки.

26.

Задачи на пропорциональное деление
Отдельным видом задач на пропорциональное деление
являются задачи на нахождение двух чисел
по их сумме и отношению.
Задача 1. Поле площадью 100 га поделили на две
части, площади которых пропорциональны
числам 2 и 3. Найдите площади этих частей.
Задача 1. Поле площадью 100 га поделили на две
части, площади которых относятся как 2 : 3.
Найдите площади этих частей.