Similar presentations:
Пропорции и отношения
1. Пропорции и отношения
2.
План учебного материала• Отношения. Основное свойство отношений.
• Пропорция. Основное свойство пропорций.
• Решение уравнений на основе свойств
пропорции.
• Случайные события. Вероятность случайного
события.
• Процентное отношение двух чисел. Процентные
расчеты. Задачи экономического содержания.
• Прямая пропорциональная зависимость.
• Задачи на пропорциональное деление .
• Окружность. Длина окружности. Круг. Площадь
круга. Круговой сектор.
• Столбчатые и круговые диаграммы.
3.
Отношения.Основное
свойство
отношений.
4.
ОтношенияЧастное двух чисел
называют отношением этих чисел.
Отношение показывает,
во сколько раз одно число больше другого
или какую часть составляет одно число от другого.
3:5
43
54
2,7:0,4
3 4
:
7 8
5.
Отношениячастное
3:5
дробь
отношения
43
54
6.
Основное свойствоотношения
Отношение двух чисел не изменится,
если каждое из них умножить или разделить
на одно и то же число,
отличное от нуля.
Оба члена пропорции можно поделить
на их общий делитель.
Отношение дробных чисел можно заменить
отношением натуральных чисел.
7.
Пропорция.Основное
свойство
пропорции.
8.
ПропорцияРавенство двух отношений
называют пропорцией.
a
c
a : b = c : d, или
b d
при b ≠ 0 і d ≠ 0
a, d – крайние члены пропорции
c, b – средние члены пропорции
9.
Основное свойствопропорции
Произведение крайних членов каждой пропорции
равно произведению ёё средних членов.
Если a : b = c : d то a · d = c · b
4 : 2 = 8 : 4 то 4 · 4 = 8 · 2
10.
Неизвестный членпропорции
Чтобы найти неизвестный крайний член пропорции,
достаточно произведение ёё средних членов
поделить на известный крайний.
Чтобы найти неизвестный средний член пропорции,
достаточно произведение ёё крайних членов поделить
на известный средний.
11.
Решениеуравнений
на основе
свойств
пропорции.
12.
Решите уравнениеx : 2 = 3 : 11
2 3 6
x
11 11
13.
Решите уравнение0 ,5 0 ,15
x
2 ,4
0 ,5 2 ,4
x
0 ,15
5 24
8
15
14.
Решите уравнение1
1
x :1 4 :
2
3
1
1
x 1 4 :
2
3
3 4 3
18
2 1
15.
Случайноесобытие.
Вероятность
случайного
события.
16.
СобытиеСобытие – то, что происходит, случается.
Событие – это явление, которое обязательно
наблюдалось большее или меньшее количество раз
при многоразовом повторении испытания.
Подкидываем монету – испытание,
появление орла – событие.
Достаём лампу из коробки – испытание,
лампа с браком – событие.
17.
СобытиеНЕВОЗМОЖНОЕ
ДОСТОВЕРНОЕ
СЛУЧАЙНОЕ
РАВНОВОЗМОЖНОЕ
18.
Вероятность случайного событияВероятностью события - называют отношение
числа благоприятных для этого события результатов
к числу всех возможных результатов.
где А – событие;
N ( A ) Р(А) – вероятность события
N – общее количество равновозможных
P( A )
событий
N N(А)и–несовместных
количество событий, которые
благоприятствуют событию
19.
Процентноеотношение
двух чисел.
Процентные расчёты.
Задачи экономического
содержания.
20.
Процентное отношениеЕсли отношение двух чисел выражают в процентах,
то его называют процентным отношением.
Один процент – это одна сотая часть
1% = 0,01
100% = 1
50% = 0,5
200% = 2
21.
Процентное отношениеСуществует три основных вида задач на проценты
нахождение процентов от числа
нахождение числа по значению его процента
нахождение процентного отношения двух чисел
22.
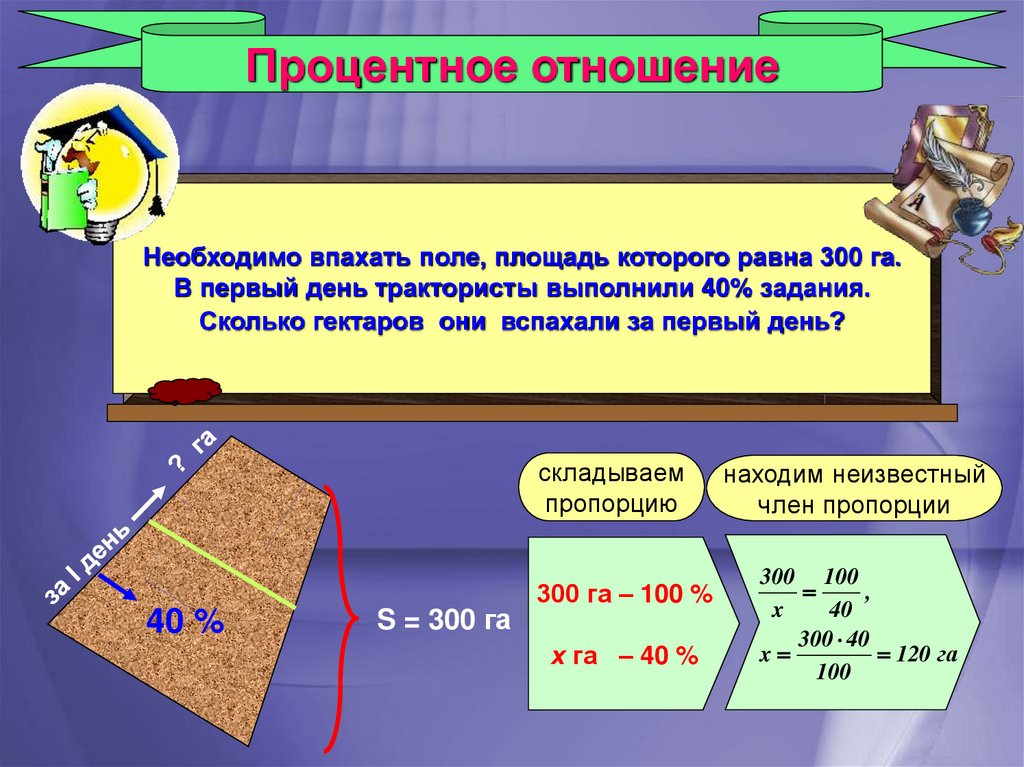
Процентное отношениеНеобходимо впахать поле, площадь которого равна 300 га.
В первый день трактористы выполнили 40% задания.
Сколько гектаров они вспахали за первый день?
40 %
S = 300 га
складываем
пропорцию
находим неизвестный
член пропорции
300 га – 100 %
300 100
,
x
40
300 40
x
120 га
100
х га – 40 %
23.
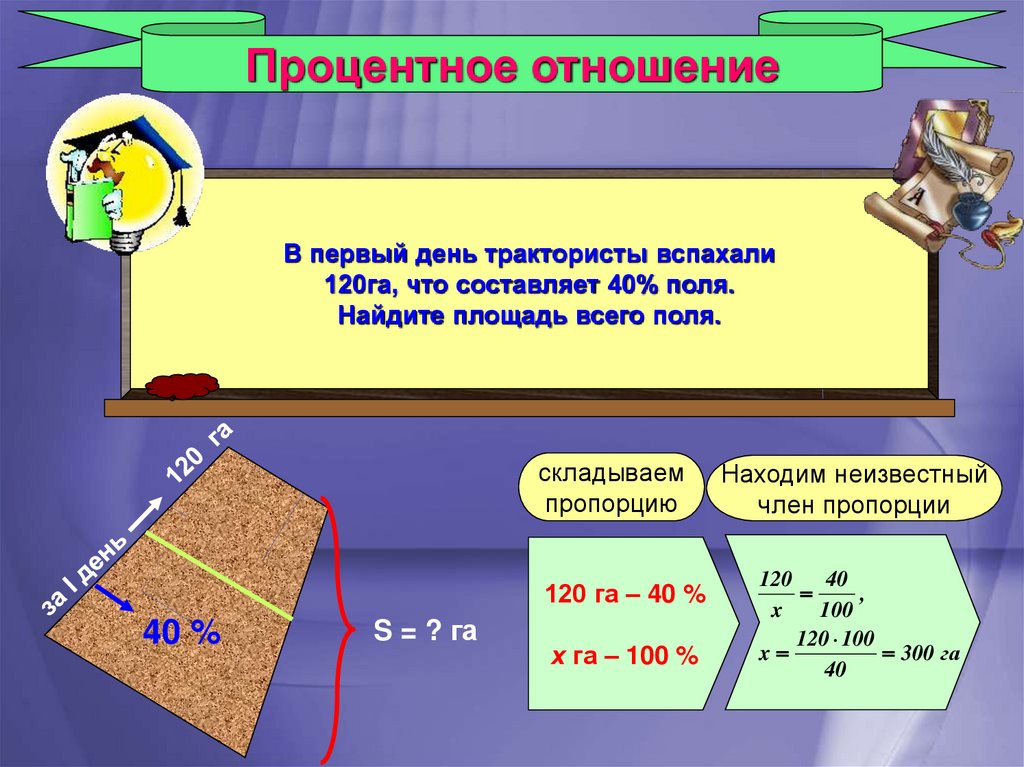
Процентное отношениеВ первый день трактористы вспахали
120га, что составляет 40% поля.
Найдите площадь всего поля.
40 %
S = ? га
складываем
пропорцию
Находим неизвестный
член пропорции
120 га – 40 %
120
40
,
x
100
120 100
x
300 га
40
х га – 100 %
24.
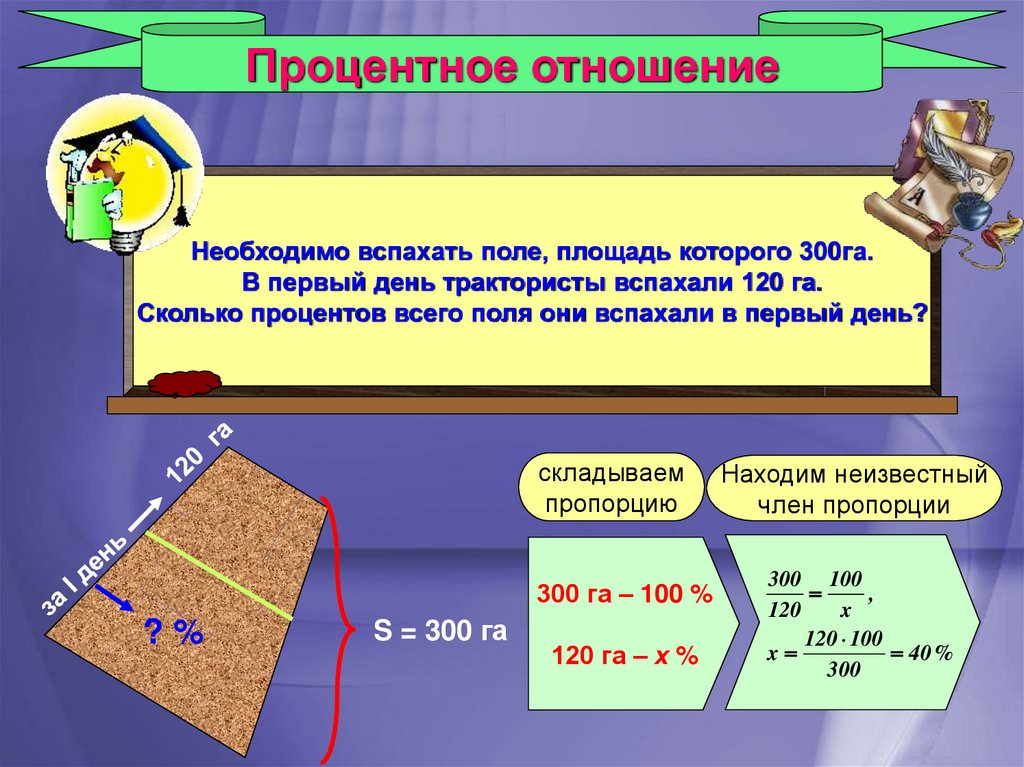
Процентное отношениеНеобходимо вспахать поле, площадь которого 300га.
В первый день трактористы вспахали 120 га.
Сколько процентов всего поля они вспахали в первый день?
?%
S = 300 га
складываем
пропорцию
Находим неизвестный
член пропорции
300 га – 100 %
300 100
,
120
x
120 100
x
40 %
300
120 га – х %
25.
Прямаяпропорциональная
зависимость.
26.
Прямая пропорциональная зависимостьДве величины называют прямо пропорциональными,
если с увеличением (уменьшением) значений
одной из них в несколько раз значение другой
увеличивается (уменьшается) во столько же раз.
Скорость, км/ч
60
60
60
60
Время, ч
1
2
3
4
Путь, км
60
120 180 240
27.
Обратно пропорциональная зависимостьДве величины называют обратно пропорциональными,
если с увеличением (уменьшением) значений
одной из них в несколько раз значения другой
уменьшаются (увеличиваются) во столько же раз.
Скорость, км/ч
50
60
100 150
Время, ч
6
5
4
Путь, км
300 300 300 300
3
28.
Задачи напропорциональное
деление.
29.
Задачи на пропорциональное делениеЧтобы поделить число на части, пропорциональные
данным числам, нужно поделить его на сумму
данных чисел и найденное частное умножить
на каждое из них.
Проволоку длиной 60 м разрезали на 3 части,
длины которых пропорциональны числам 2, 3 і 5.
Найдите длины этих частей проволоки.
30.
Задачи на пропорциональное делениеОтдельным видом задач на пропорциональное деление
являются задачи на нахождение двух чисел
по их сумме и отношению.
Задача 1. Поле площадью 100 га поделили на две
части, площади которых пропорциональны
числам 2 и 3. Найдите площади этих частей.
Задача 1. Поле площадью 100 га поделили на две
части, площади которых относятся как 2 : 3.
Найдите площади этих частей.
31.
Окружность.Длина окружности.
Круг.
Площадь круга.
Круговой
сектор.
32.
ОкружностьA
M
O
N
О – центр окружности;
ОА = r – радиус окружности
(отрезок, который соединяет любую
точку окружности с его центром);
MN = d – диаметр (отрезок, который
соединяет две точки окружности и
проходит через его центр)
Любой диаметр окружности в 2 раза
длиннее чем радиус, то есть d = 2r.
33.
Длина окружностиl d 2 r
r
O
≈ 3,14
это отношение длины окружности к диаметру
34.
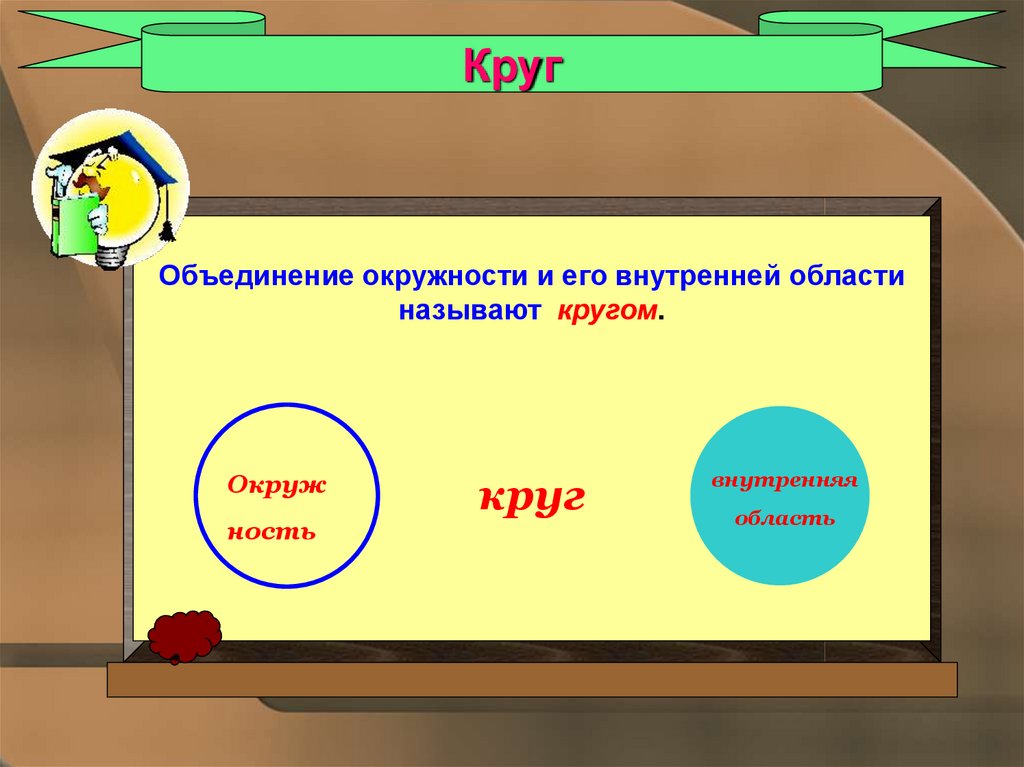
КругОбъединение окружности и его внутренней области
называют кругом.
Окруж
ность
круг
внутренняя
область
35.
Площадь кругаS r
2
r
O
36.
Круговой секторЧасть круга, ограниченная двумя его радиусами,
называется круговым сектором.
r
r
O
37.
Столбчатыеи
круговые
диаграммы.
38.
ДиаграммыДля наочного изображения числовых значений
различных величин используют диаграммы.
Слово “диаграмма” греческого происхождения,
что означает “рисунок”.
Диаграмма – это символический рисунок, который наочно
иллюстрирует соотношения между значениями величин.
Чаще всего используют диаграммы
столбчатые
39.
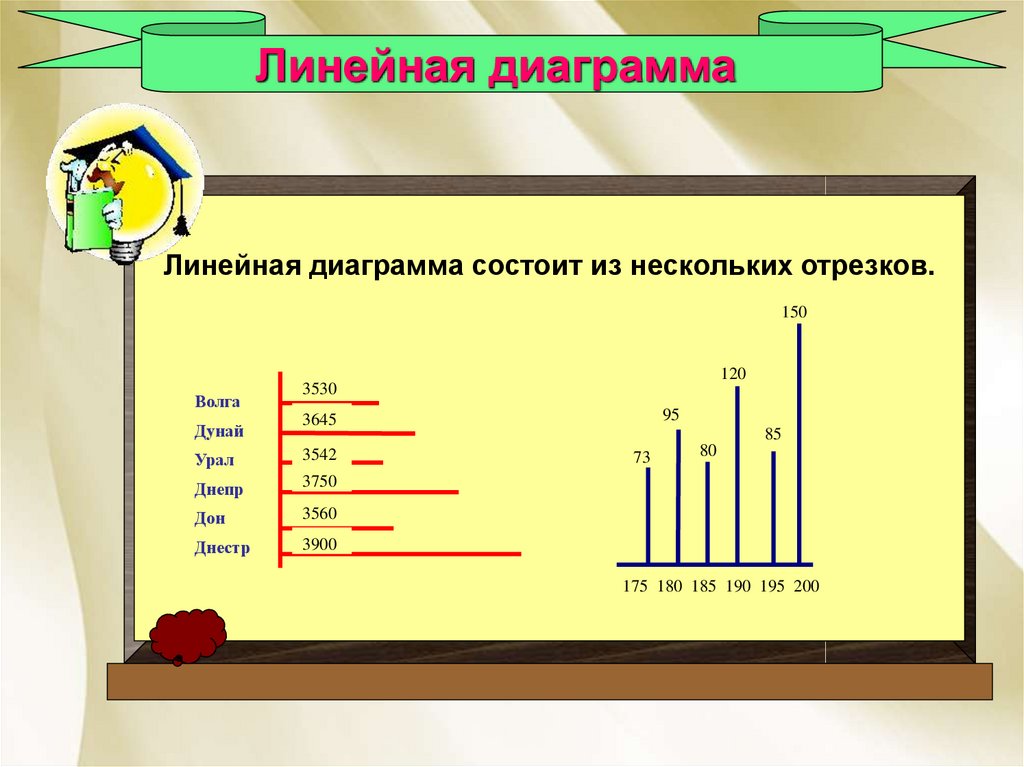
Линейная диаграммаЛинейная диаграмма состоит из нескольких отрезков.
150
Волга
120
3530
Дунай
3645
Урал
3542
Днепр
3750
Дон
3560
Днестр
3900
95
85
73
80
175 180 185 190 195 200
40.
Столбчатая диаграммаСтолбчатая диаграмма это та же линейная диаграмма,
но в ней отрезки заменены на прямоугольники.
12
10
9
10
8
8
7
6
6
5
4
4
3
2
2
1
0
1
2
3
4
5
6
7
8
9
10
0
2
4
6
8
10
12
41.
Круговая диаграммаКруговая диаграмма имеет вид круга, разделенного
радиусами на части (секторы). Поэтому такие
диаграммы называют так же секторными.
































 mathematics
mathematics








