Последовательности: основные понятия и определения

1.

Федеральное государственное бюджетное образовательное учреждение
высшего образования
«Оренбургский государственный университет»
Кафедра прикладной математики
И.Г. Руцкова
Электронный курс лекций «Математический анализ»,
часть 2
Оренбург 2017

2. Последовательности: основные понятия и определения

yn f n , n N
yn
1
2
n
, n N
y1 ,
y2 , ..., y n , ...
yn n 1
y n

3.

Последовательности: основные понятия и определения
1
1, n N ;
n
1
yn , n N .
n
yn
Пример:
yn n , n N .
yn n 1, n N ;
Пример:
1
yn , n N .
n
yn
Пример:
M 1.
m 1.
1 1
1, n N ; C 1.
n n

4. Критерий ограниченности числовой последовательности

Доказательство.
C R :
yn C , n N ;
С yn C , n N .
M=C,
M ,m R :
m yn M ,
m = - C.
n N .
m m yn M M ,
С max m , M
a a a , a R
n N .
C m yn M C ,
yn C , n N .
n N ;

5. Предел числовой последовательности

1
y n ,n N :
n
1
1
1
y1 1, y2 , y3 , ...., yn ,
2
3
n
y n n 2 ,n N :
y1 1, y2 4, y3 9, ...., yn n 2 ,
yn 1 ,n N :
n
1, n 2k 1,
y1 1, y2 1, y3 1, ...., yn
k N,
1, n 2k ,

6. Предел числовой последовательности

Пример:
Доказательство.
1
0
n
1
n
1
n
1
n0 1,
1 n
n
1

7. Задания к практическому занятию

8. Предел числовой последовательности

yn A yn A A yn A
yn A
yn A
yn A ; A
yn U A

9. Предел числовой последовательности

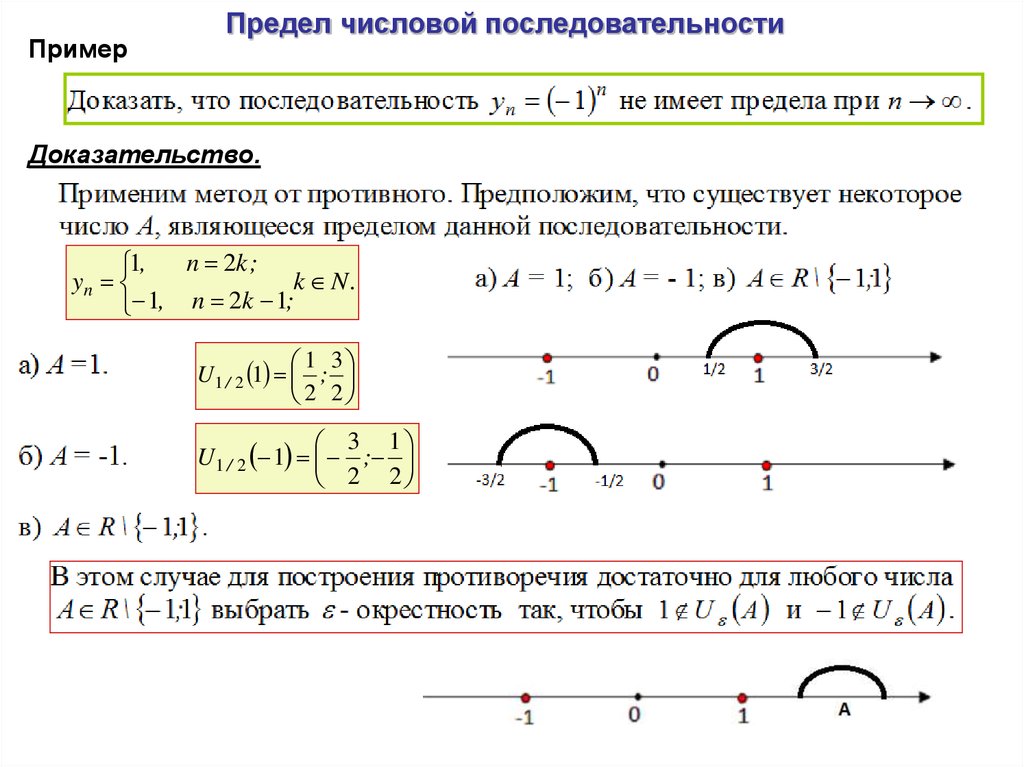
Пример
Предел числовой последовательности
Доказательство.
n 2k ;
1,
yn
k N.
1, n 2k 1;
1 3
U1 / 2 1 ;
2 2
3 1
U1 / 2 1 ;
2 2

10. Свойства последовательностей, имеющих предел

Доказательство.
0
B A
2
lim y n A n1 N : yn U A , n n1
n
lim y n B n2 N : yn U B , n n2
n
n0 max n1 ; n2
n n0
y n U A ,
y n U B ;
y n U A U B
Получаем противоречие.

11.

Свойства последовательностей, имеющих предел
Доказательство.
A lim yn 0 n0 N : yn A , n n0
n
n0 1 N : yn A 1, n n0
1
a b a b,
yn A yn A 1,
a ,b R
n n0 1 ;
yn A 1,
yn A 1,
n n0 1
С maх А 1; y1 ; y2 ;...; yn0 1 1
yn C , n N ,
С R .
n n0 1 ;

12.

Свойства последовательностей, имеющих предел
Доказательство. Изучить самостоятельно.
Доказательство. Изучить самостоятельно

13.

Свойства последовательностей, имеющих предел
Доказательство. Изучить самостоятельно.

14.

Свойства последовательностей, имеющих предел
Доказательство.
lim zn A
n
n1 N : zn U A ,
A zn A ,
lim yn A
n
n0 max n1 , n2
A xn A ,
n n1
n2 N : yn U A ,
A yn A ,
n n1
n n2
n n2
A z n xn y n A ,
n n0
xn A , n n0
n n0

15.

Задание к практическому занятию

16.

Свойства последовательностей, имеющих предел
Доказательство. 1)
lim yn z n A B 0 n0 N : yn zn A B , n n0
n
.
yn zn A B yn A zn B
yn A zn B ,
lim yn A
n1 N : yn A , n n1
2
2
2
lim z n B
n2 N :
2
n
n
n0 max n1 , n2
2 2
n N
z n B , n n2
2
2
yn zn A B ,
2
2
n n0

17. Задание к практическому занятию

Задание. Доказать утверждения 2), 3) , 4) теоремы 7.

18.

Свойства последовательностей, имеющих предел

19.

Задания к практическому занятию

20. Монотонные последовательности

21. Признак существования предела у монотонной последовательности

Доказательство.
Кудрявцев Л.Д. «Курс математического анализа». – М: Высшая школа, 1981
Доказательство.
1) 0 q 1.
уn 1 q n 1 q q n q уn уn , n N ;
zn yn 1 q
n 1
,n N :
n
lim zn A,
1 q 0.
n
lim q 0;
n
0 уn q n 1, n N ;
A R :
lim yn A.
n
lim zn lim yn 1 lim q n 1 lim q q n lim q yn q A
n
lim zn qA
n
n
2)
yn q n , n N :
n
n
A 1 q 0,
A q A,
n
n
q q n q n q n q , n N ;
lim 1 q 1 0 0.
lim q
n
n
n
n
n
A 0
0 q 1.
lim q n 0
n

22. Признак существования предела у монотонной последовательности

Доказательство.
Кудрявцев Л.Д. «Курс математического анализа». – М: Высшая школа, 1981
n
1
lim 1 e ,
n
n
Число е - иррациональное и трансцендентное.
е 2,7182818284 59045 ...

23. Задания к практическому занятию

24.

Фундаментальные последовательности
A R : lim yn A
Доказательство. 1)
n
ym yn ym A A yn ym A A yn ym A yn A , n,m N .
0 n0 N :
ym yn
ym A , m n0 ,
2
2
2
yn A , n n0 .
2
, n,m n0 .
2) Кудрявцев Л.Д. «Курс математического анализа». – М: Высшая школа, 1981.

25. Бесконечно малые последовательности

Доказательство.
n n 1 ,
n yn A, n N ;
lim n lim yn A A A 0,
n
n
yn A n , n N .
lim yn lim A n A 0 A.
n
n

26. Бесконечно малые последовательности

Доказательство.
lim yn zn 0
n
0 n0 N : yn zn , n n0
yn zn yn zn C yn ,
n N ;

27.

Бесконечно малые последовательности

28. Задание к практическому занятию

29.

Бесконечно большие последовательности
Пример:
lim n 2 .
.
n
Доказательство.
yn M n 2 M n 2 M
n0 max 1, M 2 1 :
n M 2;
n 2 M , n n0

30.

Бесконечно большие последовательности
Доказательство.
lim yn zn M 0 n0 M N : yn zn M , n n0 M
n
yn zn yn zn C yn ,
M 0
M
n0 M n1 :
C
yn zn C
n N .
M
M,
C
n n0 M

31.

Бесконечно большие последовательности
Доказательство.
.
lim zn A, A 0 :
n
n1 A N :
zn
A
, n n1 ;
2
A
yn zn yn zn yn , n n1
2
n0 M max n1 A ,n2 M
M 0 n0 M max n1 ,n2 :
yn z n C
lim yn zn
n
M
M,
C
n n0 M

32.

Бесконечно большие последовательности
Доказательство. 1)
1
1
1
M
M yn
yn
yn
M
M 0 n0 M N :
1
M , n n0 M ,
yn
1
n yn
lim

33. Задание к практическому занятию

34.

Бесконечно большие последовательности

35.

Бесконечно большие последовательности

36. Подпоследовательности

Доказательство.
Кудрявцев Л.Д. Курс математического анализа. – М: Высшая школа, 1981, Т.1., стр. 63-64.
Доказательство. Доказательство проведите самостоятельно.