Similar presentations:
Определенный интеграл
1. Определенный интеграл
bf x dx F x F b F a
b
a
a
– формула Ньютона-Лейбница.
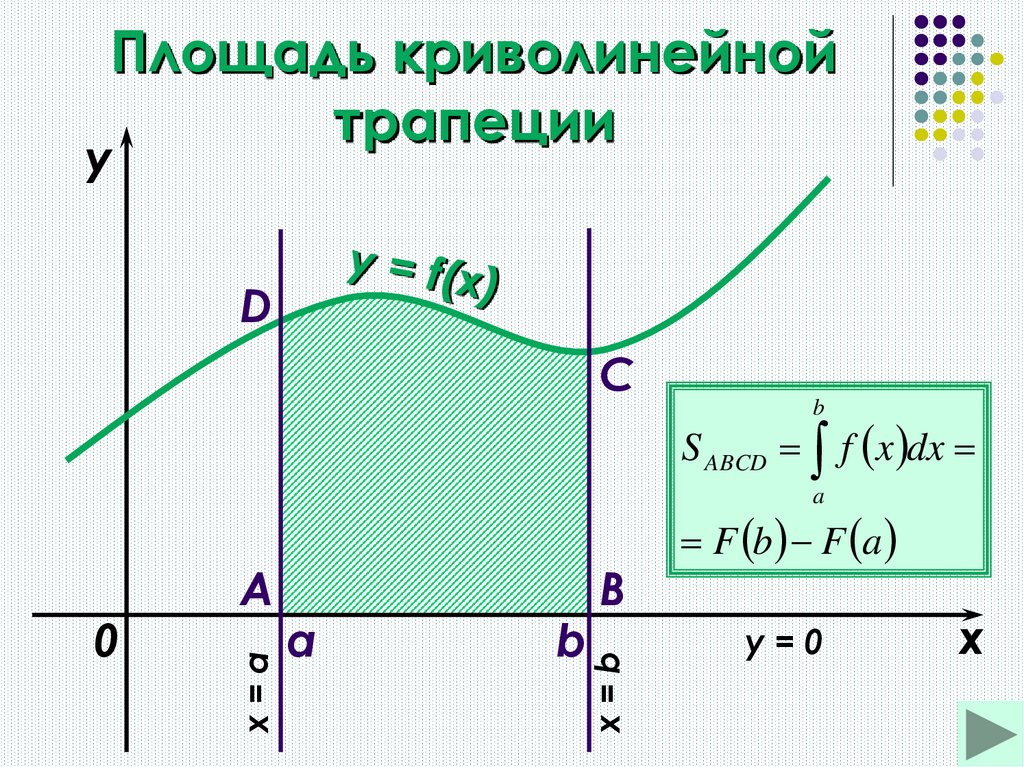
Геометрический смысл определенного интеграла
заключается в том, что определенный интеграл
равен
площади
криволинейной
трапеции,
образованной линиями:
сверху ограниченной кривой у = f(x),
и прямыми у = 0; х = а; х = b.
2. Вычисление определенного интеграла
3x 2 x 1 dx x x x2
2
3
2
2
1
1
23 22 2 13 12 1 6 1 5
10
3
2 x 6 x 6
x 6 dx
3
3
10
2 10 6 10 6 2 3 6 3 6 80
2
18 7
3
3
3
3
3. Площадь криволинейной трапеции
yD
C
b
S ABCD f x dx
a
a
b
B
x=b
x=a
0
A
F b F a
y=0
x
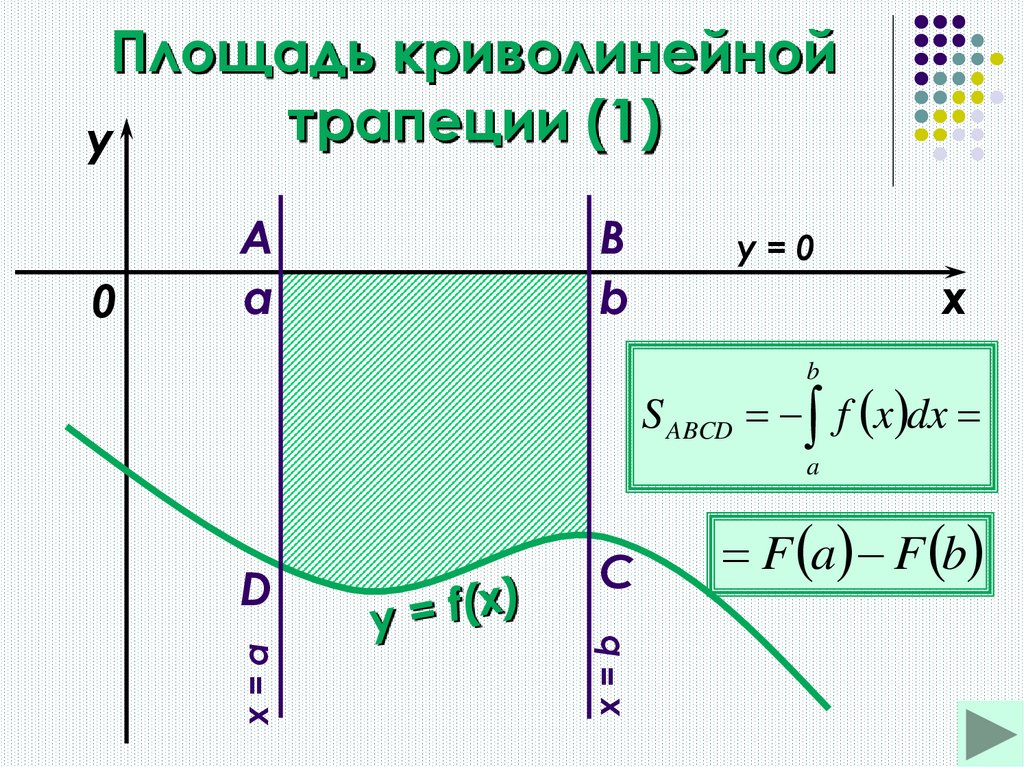
4. Площадь криволинейной трапеции (1)
yB
b
y=0
x
b
S ABCD f x dx
D
C
x=b
a
x=a
0
A
a
F a F b
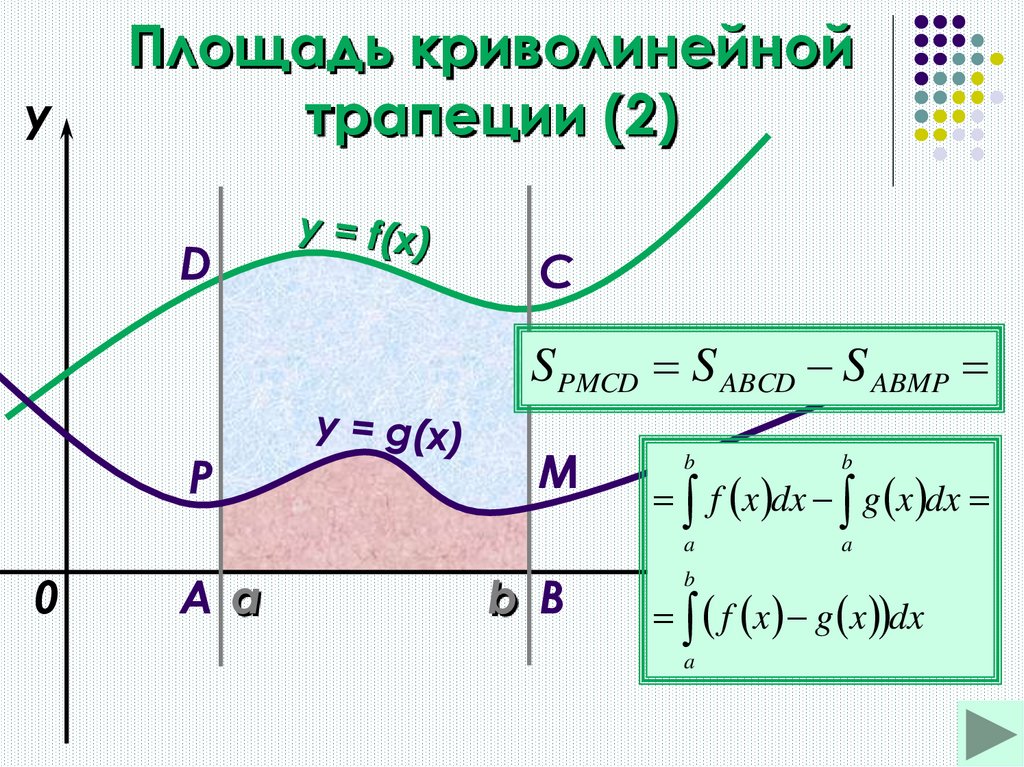
5.
yПлощадь криволинейной
трапеции (2)
D
C
S PMCD S ABCD S ABMP
P
0
Aa
M
b B
b
b
a
a
f x dx g x dx
f x g x dxx
b
a
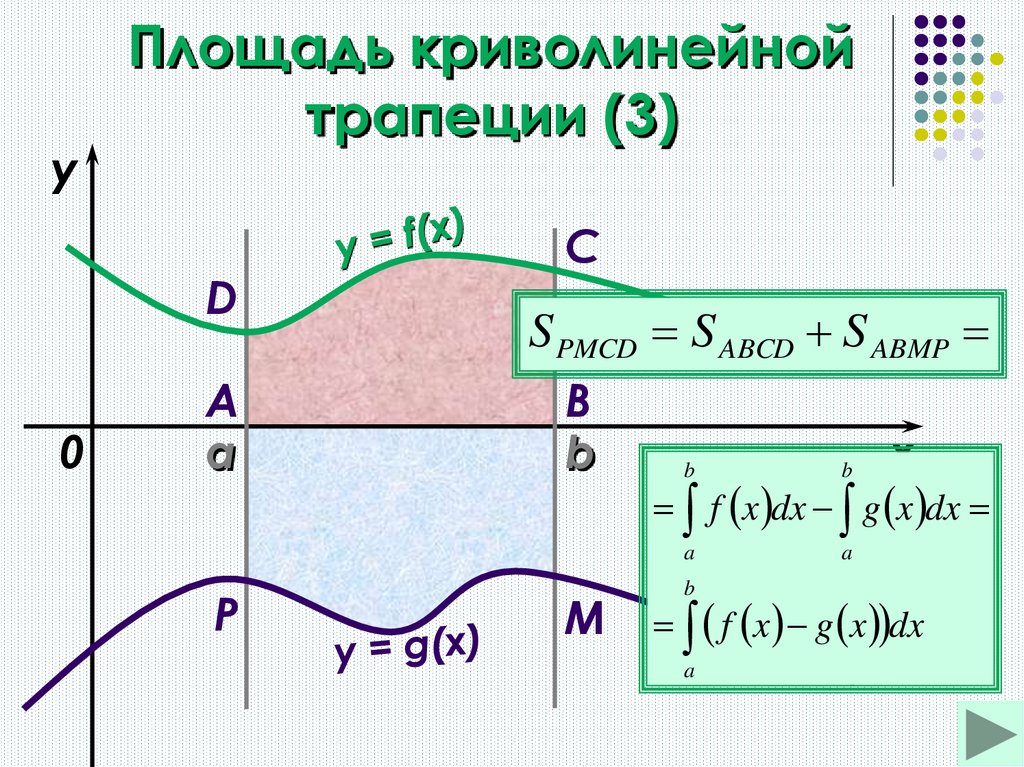
6.
yПлощадь криволинейной
трапеции (3)
D
0
A
a
P
C
S PMCD S ABCD S ABMP
B
b
M
b
b
a
a
x
f x dx g x dx
b
f x g x dx
a
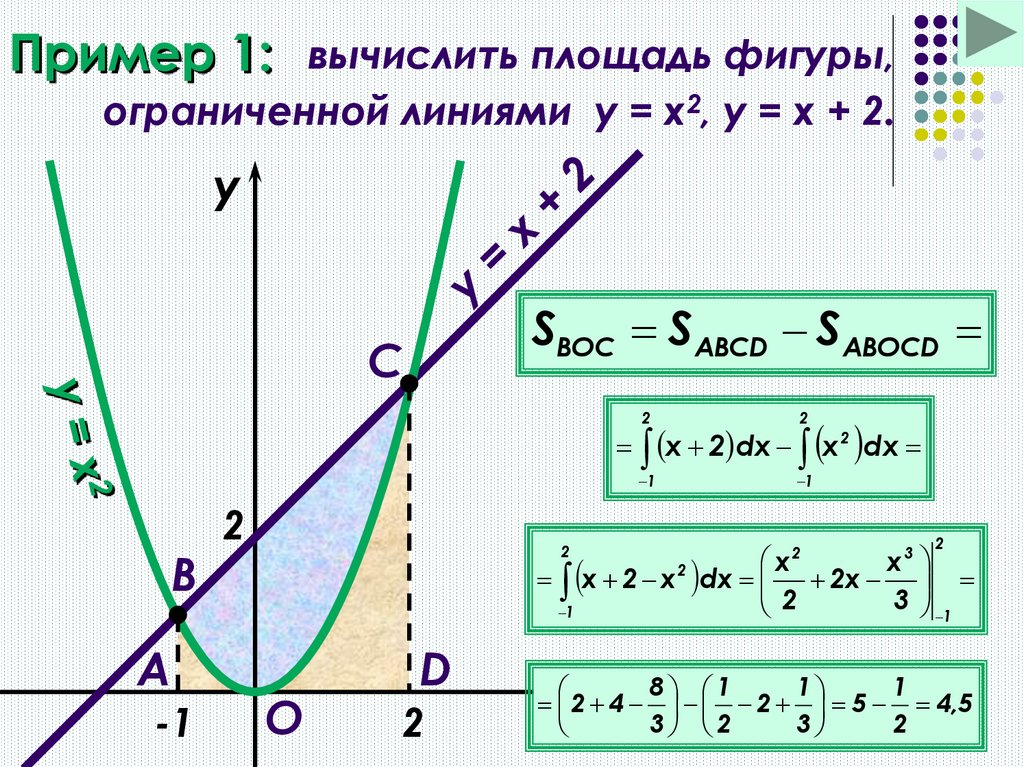
7. Пример 1:
вычислить площадь фигуры,ограниченной линиями y = x2, y = x + 2.
y
SВОС SABCD SABOCD
C
2
2
1
1
x 2 dx x 2 dx
B
A
-1
2
2
2
x
x
х 2 х 2 dx 2x
3 1
2
1
O
D
2
2
3
8 1
1
1
2 4 2 5 4,5
3 2
3
2
x
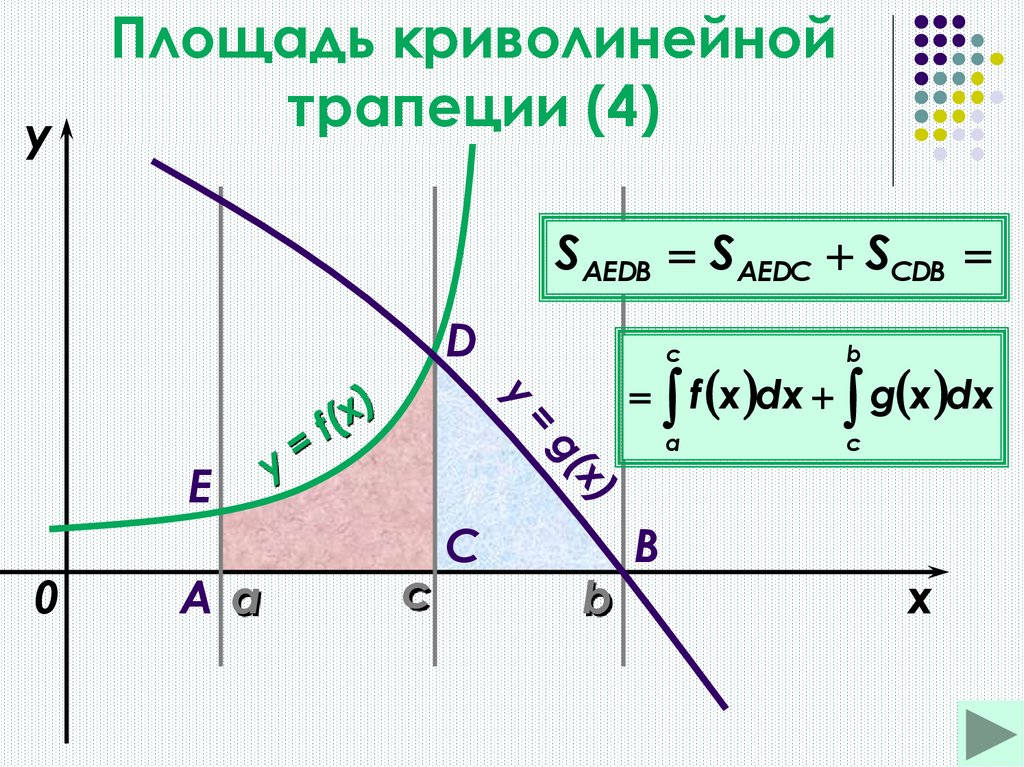
8.
yПлощадь криволинейной
трапеции (4)
SАЕDВ SAEDC SСDB
D
с
b
a
с
f x dx g x dx
Е
0
Aa
с
C
b
B
x
9.
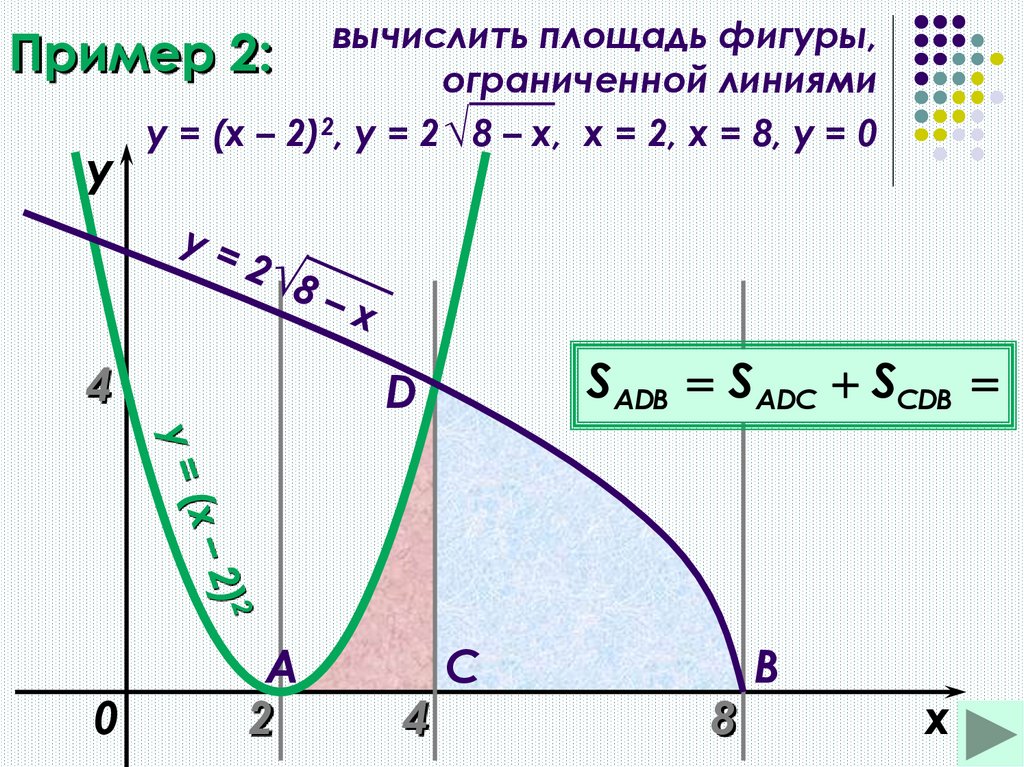
вычислить площадь фигуры,Пример 2:
ограниченной линиями
y = (x – 2)2, y = 2 √ 8 – x, х = 2, х = 8, у = 0
y
4
0
SАDВ SADС SСDB
D
A
2
4
C
8
B
x
10.
вычислить площадь фигуры,Пример 2:
ограниченной линиями
y = (x – 2)2, y = 2 √ 8 – x, х = 2, х = 8, у = 0
3 4
x 2
x - 2 dx 2 8 - хdx
4
2
2
8
4
3
8
4 8 x 8 x
3
2
4
4 2 3 2 2 3 4 8 8 8 8 4 8 4 8 4
3
3
3
3
8 32 40
1
13
3 3
3
3



 mathematics
mathematics








