570.59K

Category:

programming

Разведочный анализ данных. Data Mining (лекция 2)

1.

Data Mining
ЛЕКЦИЯ 2
Зарецкий М.В.
кафедра ВТиП

Exploratory Data Analysis (EDA)
Разведочный анализ данных
(РАД)
•РАД – предварительный анализ данных с
целью
выявления
наиболее
общих
зависимостей,
закономерностей
и
тенденций,
характера
и
свойств
анализируемых
данных,
законов
распределения анализируемых величин.
Применяется при недостатке априорных
сведений о связи изучаемых объектов.

3.

•При выполнении РАД учитывается
сравнительно большое число признаков.
•Термин «Разведочный анализ данных»
был введен Дж. Тьюки (Джон Уайлдер
Тьюки, John Wilder Tukey, 1915 – 2000).
•Джон Тьюки сформулировал задачи
РАД:
•- максимальное «проникновение» в
данные;
•- выявление основных структур;
•- выбор наиболее важных переменных;

4.

•- обнаружение отклонений и аномалий;
•- проверка основных гипотез;
•- разработка начальных моделей.
•Решение каждой из перечисленных
задач является непростым, пути решения
– неочевидны.
•Никакое «проникновение» в данные без
тесного взаимодействия со специалистом
– инженером, врачом, финансистом –
невозможно.
•Какие структуры основные, а какие –
нет?

5.

•Что перед нами – аномалия или редко
наблюдаемый важный вариант?
•Формулировка и проверка гипотез,
разработка и апробация моделей – тут
не все просто.
•Пример. Закон Ома для участка цепи без
ЭДС: U = IR (надеюсь, смысл всем
понятен) .
•Зависимость хорошо обоснована
теоретически.

6.

•Вряд ли есть смысл заново подбирать
эту зависимость по экспериментальным
данным.
•А вот если мы решим, учесть изменение
сопротивления, тогда придется
определить перечень факторов, от
которых, на наш взгляд, может зависеть
сопротивление, выбрать наиболее
существенные, построить модели и
проверить их адекватность.

7.

Структурирование данных
•Напомню, что данными называют
представленные в формализованном виде
факты и идеи. Например, числа, текст в
виде последовательности букв
(иероглифов), световые (звуковые)
сигналы и т.д.
•Данные поступают из многих источников
и в самом разном виде.

8.

•Информация извлекается из данных.
•Data Mining занимается методами
извлечения информации из данных.
•Анализируемые данные должны быть
структурированы – каким-либо заданным
образом упорядочены (база данных,
хранилище данных и т.д.)
•Рассматривают два основных типа
структурированных данных – числовой и
категориальный.

9.

•Числовые данные подразделяются на
непрерывные и дискретные.
•Непрерывные могут принимать любое
значение в заданном интервале.
Например, длительность какого-либо
процесса.
•Пример дискретных – количество
объектов, событий.
•Деление условное. Например, в
компьютере представление чисел
дискретно.

10.

•Во многих моделях мы переходим от
дискретных величин к непрерывным –
модели массового обслуживания и т.п.
•Для непрерывных и дискретных
числовых данных определены понятия
порядка: «больше» «меньше».
•Категориальные данные имеют
фиксированный набор значений.
•Двоичные данные принимают только
значения 0/1, True/False
Порядковые данные строго упорядочены.

11.

• Для порядковых величин можно
отнести отношения «больше»
«меньше».
• Рассмотрим детали.
• «Прямоугольные» данные – матрица, в
которой строки представляют собой
записи (случаи), а столбцы – признаки
(переменные).
• Имеются различия в терминологии
статистики и Data Science.

12.

«Непрямоугольные» данные.
Объектное, сетевое представление
данных.
Внимание! Существует
противоречивость в терминологии.
Часто в информатике словом «выборка»
называют одну строку в таблице. В
статистике этим словом правильнее
будет назвать все строки в таблице.

13.

Оценки центрального
положения
•Перечислим эти оценки. Многие из них
хорошо знакомы, другие, возможно,
встретятся впервые. В представленных
фрагментах кода на языке R показано
вычисление всех основных оценок
центрального положения.

14.

Приведем список оценок центрального
положения:
-среднее (mean);
-среднее взвешенное (weighted mean);
-медиана (50 процентиль) (median);
-медиана взвешенная (weighted median);
- среднее усеченное (trimmed mean);
- робастный (устойчивый) (robust);
- выброс (предельное значение) (outlier).

15.

Прокомментируем некоторые термины.
Выброс – значение данных, которое
сильно отличается от остальных.
Например, у студента указан возраст 11
лет (не слишком ли он юн?), или 41 год
(не староват ли он?)
Отметим, что часто «выбросы» несут
ценную информацию. Поэтому отсев
выбросов не может выполняться
полностью автоматически.

16.

Среднее усеченное – среднее всех
значений, оставшихся после отсева
выбросов.
Робастный – нечувствительный к
выбросам.
Отдельно рассмотрим медиану и
робастные оценки.

17.

Медиана – число, расположенное в
сортированном списке посередине. Если в
списке четное число элементов, медиана
– среднее арифметическое значений,
которые делят список на верхнюю и
нижнюю половины.
Медиана намного менее чувствительна к
резко отличающимся от остальных
данным.

18.

Рассмотрим пример. Пусть у случайным
образом отобранной группы людей
доходы (в тысячах рублей) равны:
17,35,77,53,29,71,9876.
Вычислите среднее значение и медиану.
Как они изменятся, если доходы «богача»
возрастут в 10 раз?
Рассмотрим нахождение перечисленных
оценок средствами языка R.

19.

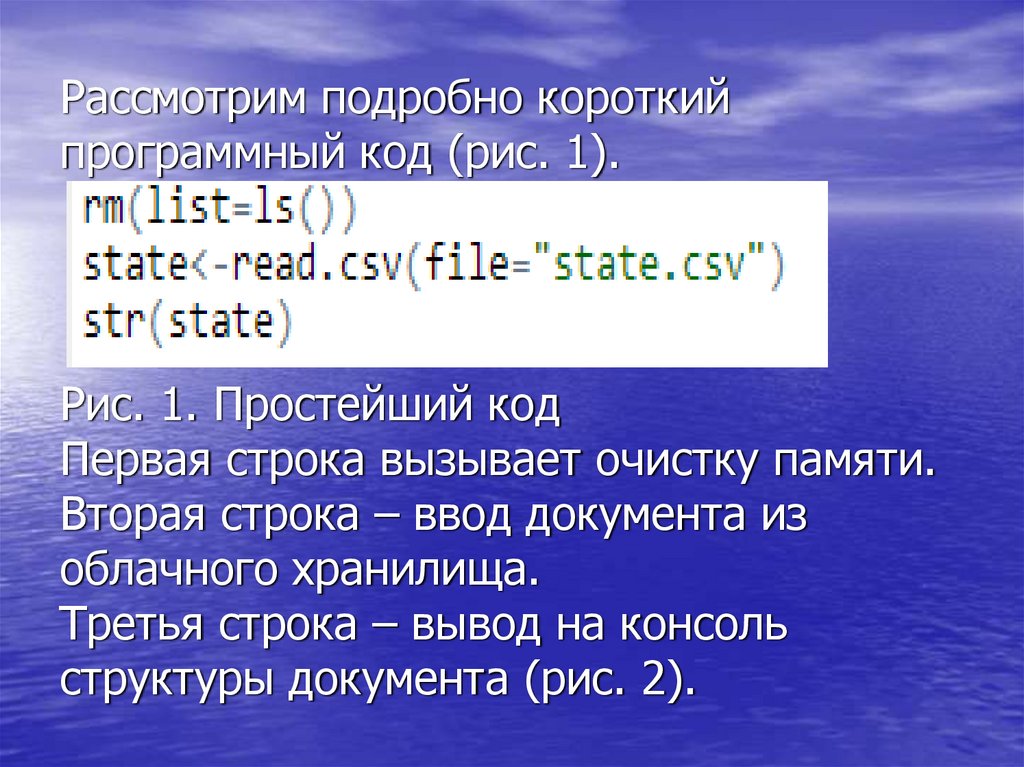
Рассмотрим подробно короткий
программный код (рис. 1).
Рис. 1. Простейший код
Первая строка вызывает очистку памяти.
Вторая строка – ввод документа из
облачного хранилища.
Третья строка – вывод на консоль
структуры документа (рис. 2).

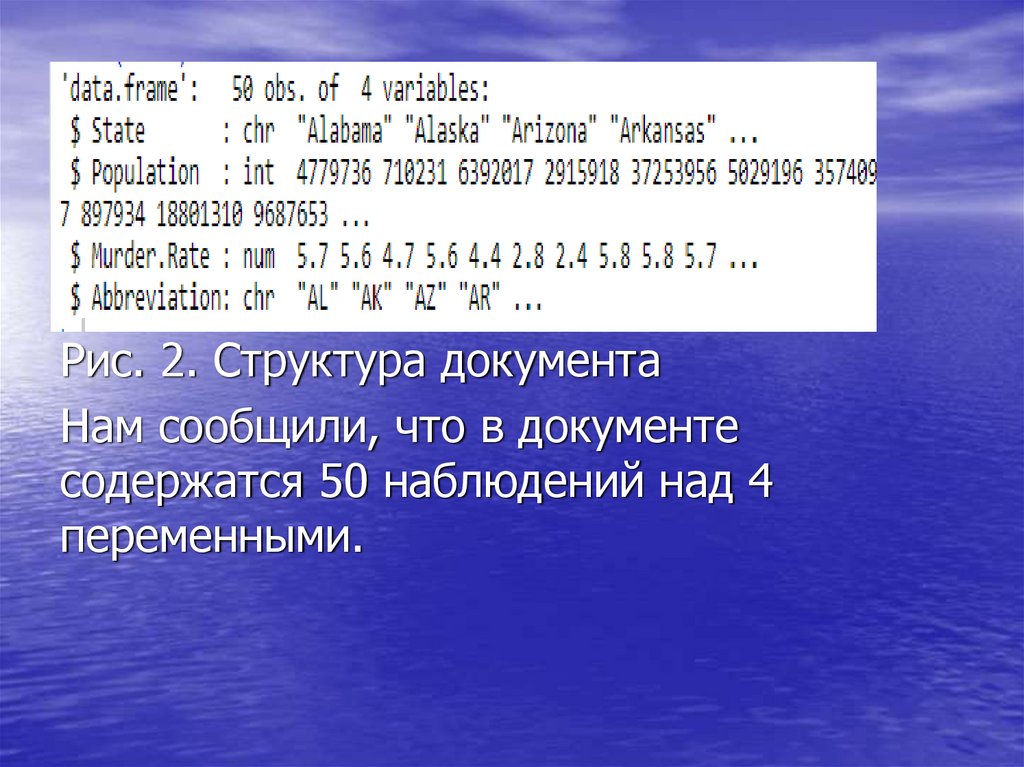
20.

Рис. 2. Структура документа
Нам сообщили, что в документе
содержатся 50 наблюдений над 4
переменными.

21.

Переменные:
- штат (State) – имя штата;
- население (Population) – население;
- уровень убийств (Murdrer.Rate) в
единицах на 100000 человек в год;
- сокращенное имя (Abbreviation).
Теперь найдем среднее, среднее
усеченное и медиану численности
населения (рис. 3)

22.

Рис. 3. Вычисление статистических
характеристик
Обратите внимание на обращение к
столбцу таблицы – так требует синтаксис
языка R.
Все вычисленные значения собираются в
массив output, который затем выводится.

23.

Получаем результат (рис. 4).
Рис. 4. Результат вычислений
статистических характеристик
Выведены среднее, среднее усеченное и
медиана.
При вычислении среднего усеченного
были отброшены по 0.1 наблюдений из
отсортированного массива (trim=0.1).

24.

Среднее больше среднего усеченного,
которое больше медианы. Вычислим
теперь среднестатистические
характеристики. Для этого мы должны
учитывать численность населения в
качестве весового коэффициента.
Вычислим взвешенное среднее и
взвешенную медиану. Для вычисления
взвешенной медианы установим пакет и
библиотеку matrixStats (рис. 5).

25.

Рис. 5. Установка пакета и библиотеки
matrixStats.
Функция install.packages() устанавливает
пакеты, размещенные в CRAN. Для
пакетов, размещенных в других
хранилищах, их расположение
специально указывается.

26.

Функция library() устанавливает
библиотеку. Совпадение параметров при
вызове функций install.packages() и
library(имен пакета и библиотеки) не
обязательно и встречается не очень
часто. Пакет может содержать много
библиотек.
В некотором идейном родстве с
install.packages() и library() состоят
функции Python pip install… (в Google
Colaboratory - !pip install…) и import…

27.

Рис. 6. Протокол установки пакета.
Внимание! Протокол установки пакета
выводится красными символами. Это не
аварийное сообщение!

28.

Теперь мы можем вычислить
статистические характеристики (рис. 7).
Рис. 7. Вычисление взвешенных
статистических характеристик
Полученные значения будут очень
близкими. Проверьте!

29.

Оценки вариабельности
•Оценки центрального положения не
дают точного представления об
изучаемом объекте (явлении).
•Вариабельность (дисперсность)
характеризует кучность (плотность)
значений – близки они друг к другу или
разбросаны.

30.

Приведем список оценок вариабельности:
- отклонения, ошибки, остатки
(deviations);
- дисперсия (variance);
- стандартное отклонение (standard
deviation);
- среднее абсолютное отклонение
(манхэттенская норма) (mean absolute
deviation);

31.

- медианное абсолютное отклонение от
медианы (median absolute deviation
from the median);
- размах (range);
- порядковые статистики (ранг) (order
statistics);
- процентиль (квантиль) (percentile);
- межквартильный размах (interquartile
range).

32.

33.

Дисперсия, стандартное отклонение,
среднее абсолютное отклонение не
устойчивы к выбросам и предельным
значениям.
Робастной оценкой вариабельности
является медианное абсолютное
отклонение от медианы – медианное
значение модулей отклонений компонент
вектора наблюдений от медианы.

34.

Замечание о процентилях.
В наборе данных P-й процентиль
является таким значением, что, по
крайней мере, P процентов элементов
данного набора принимают это значение
или меньшее и, по крайней мере, (100-P)
процентов элементов данного набора
принимают это значение или большее.
Очевидно, что при P=50 процентиль
является медианой.

35.

Распространенной мерой вариабельности
является межквартильный
(интерквартильный) размах – разность
между 25-м и 75-м процентилями.
Рассмотрим программную реализацию
следующих оценок вариабельности на
языке R:
- стандартного отклонения;
- интерквартильного размаха;
- медианного абсолютного отклонения от
медианы (рис. 8).

36.

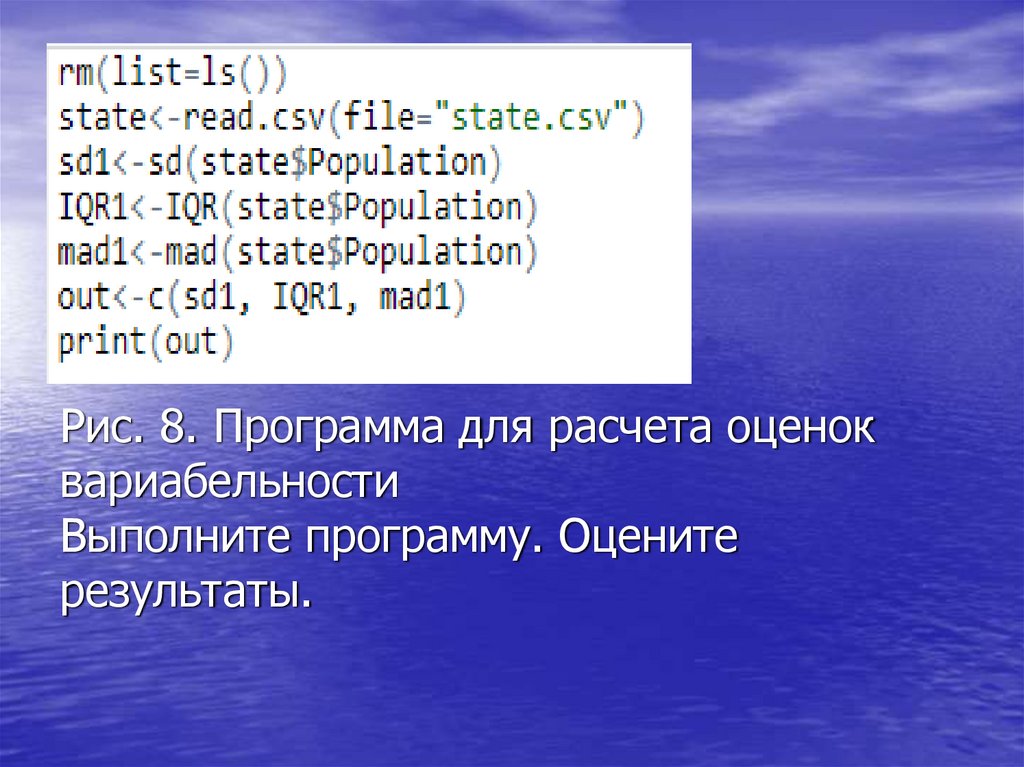
Рис. 8. Программа для расчета оценок
вариабельности
Выполните программу. Оцените
результаты.

37.

Обследование распределения
данных
•Рассмотрим некоторые способы
наглядного представления данных с
помощью наглядных средств.
•Перечислим основные понятия:
•- коробчатая диаграмма (ящик с усами)
(boxpot);
•- частотная таблица (frequency table);
•- гистограмма (histogram);

38.

•- график плотности (density plot).
•Построим коробчатую диаграмму (рис.
9).
•Рис. 9. Код для построения коробчатой
диаграммы
•Рис. 10. Коробчатая диаграмма

39.

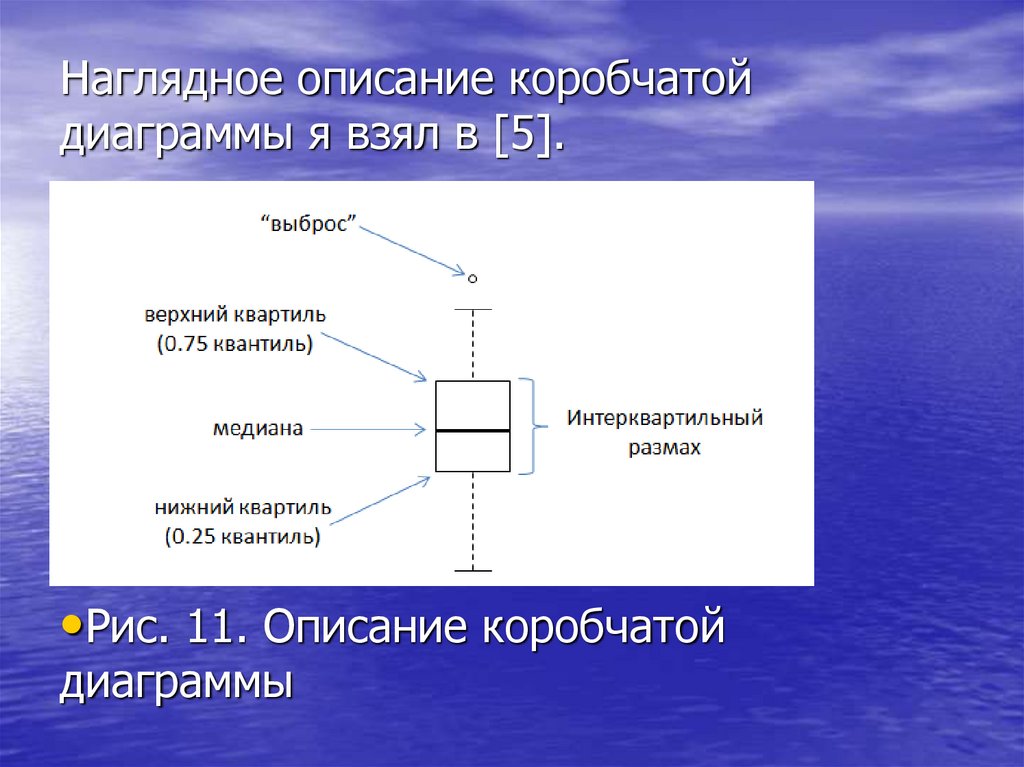
Наглядное описание коробчатой
диаграммы я взял в [5].
•Рис. 11. Описание коробчатой
диаграммы

40.

Построим теперь частотную таблицу.
•Рис. 12. Построение частотной таблицы
•Рис. 13 Частотная таблица

41.

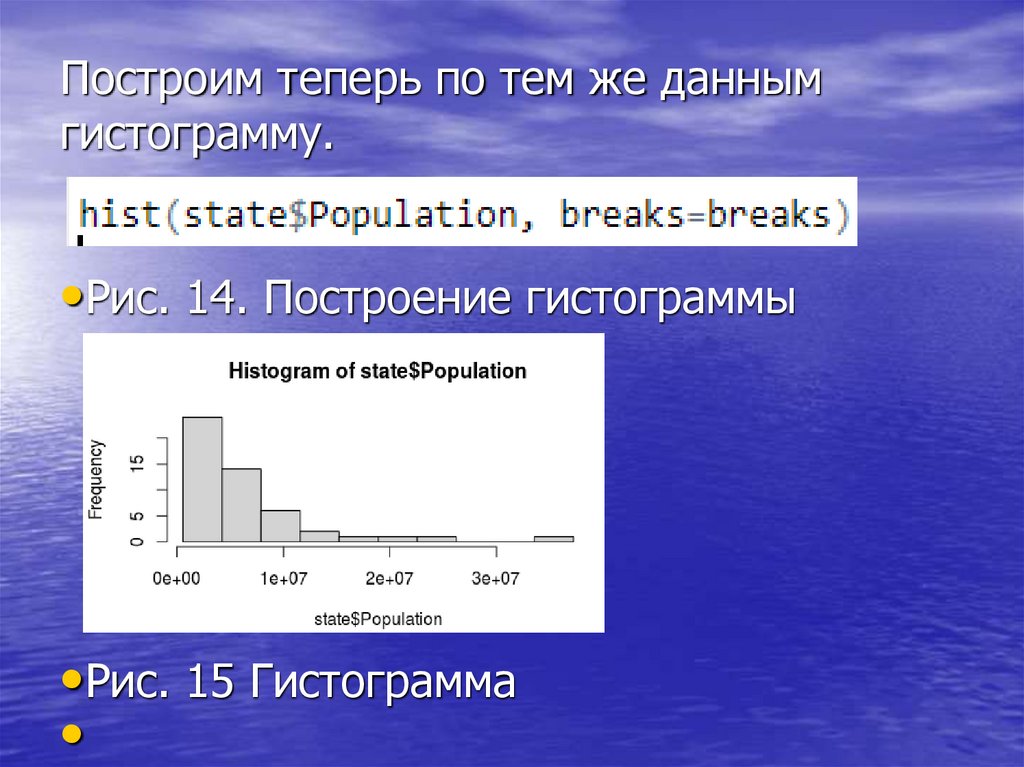
Построим теперь по тем же данным
гистограмму.
•Рис. 14. Построение гистограммы
•Рис. 15 Гистограмма

42.

Дополним гистограмму аппроксимацией
плотности.
•Рис. 16. Построение аппроксимации
плотности
•Рис. 17 Аппроксимация плотности

43.

Двоичные и категориальные
данные
•Представление о двоичных и
категориальных данных дают:
•- мода - mode;
•- математическое ожидание (ожидаемое
значение) – expected value;
•- столбчатая диаграмма – bar chart;
•- круговая диаграмма – pie chart.

44.

•Рис. 18 Построение столбчатой
диаграммы
•Рис. 19. Столбчатая диаграмма

45.

•Сейчас рассмотрим нахождение моды и
ожидаемого значения (оценки
математического ожидания). Также
рассмотрим несколько очень полезных
функций языка R и написание
пользовательской функции на R.
•Пример. Тридцати парам, подавшим
заявление о регистрации брака задали
вопрос: «Сколько детей вы собираетесь
родить» ?
• Получены такие ответы:

46.

21352122610523213272312
2452325
•Пусть наши данные занесены в
текстовый файл в виде столбца (рис. 20).
•Рис. 20 Фрагмент исходных данных

47.

•Сохраним этот файл под именем
“Future_Children.txt” и загрузим его в
облачное хранилище Rstudio Cloud.
•Прочитаем этот файл и подготовим его к
обработке (рис. 21).
•Рис. 21 Ввод и подготовка данных

48.

Что делается в представленном на рис.
21 фрагменте кода?
Очищается память. В переменную
input.data прочитывается текстовый
файл "Future_Children.txt". Указываем, что
каждое число читается с новой строки
(разделитель – перевод строки). Во
введенных данных два столбца. Мы
извлекаем данные из столбца $V1 и
сортируем их по возрастанию. Получаем
массив сырых данных - raw.data.
Сохраняем его в файле “raw.csv”.

49.

Из сортированного массива сырых данных
получаем массив уникальных значений
unique.data. Затем получаем массив
tab.data, каждый элемент которого
содержит количество появлений одного
из уникальных значений в массиве сырых
данных.
В нашем случае
unique.data: 0 1 2 3 4 5 6 7
tab.data
: 1 5 12 5 1 4 1 1
Прооверьте!

50.

С помощью функции data.frame
объединяем полученные массивы в
структуру Children. Полученную структуру
сохраняем на облачном носителе в файле
"Children.csv".
Данный фрагмент выполняется отдельно.
Для дальнейшей обработки используются
файлы “raw.csv” и "Children.csv".
Программа обработки данных не должна
зависеть от того, как были получены эти
файлы.
Точка внутри имен – дань традиции R!

51.

Теперь воспользуемся сохраненными
файлами. Сначала построим столбчатую
диаграмму (рис. 22-23).
Рис. 22. Программа для построения
столбчатой диаграммы

52.

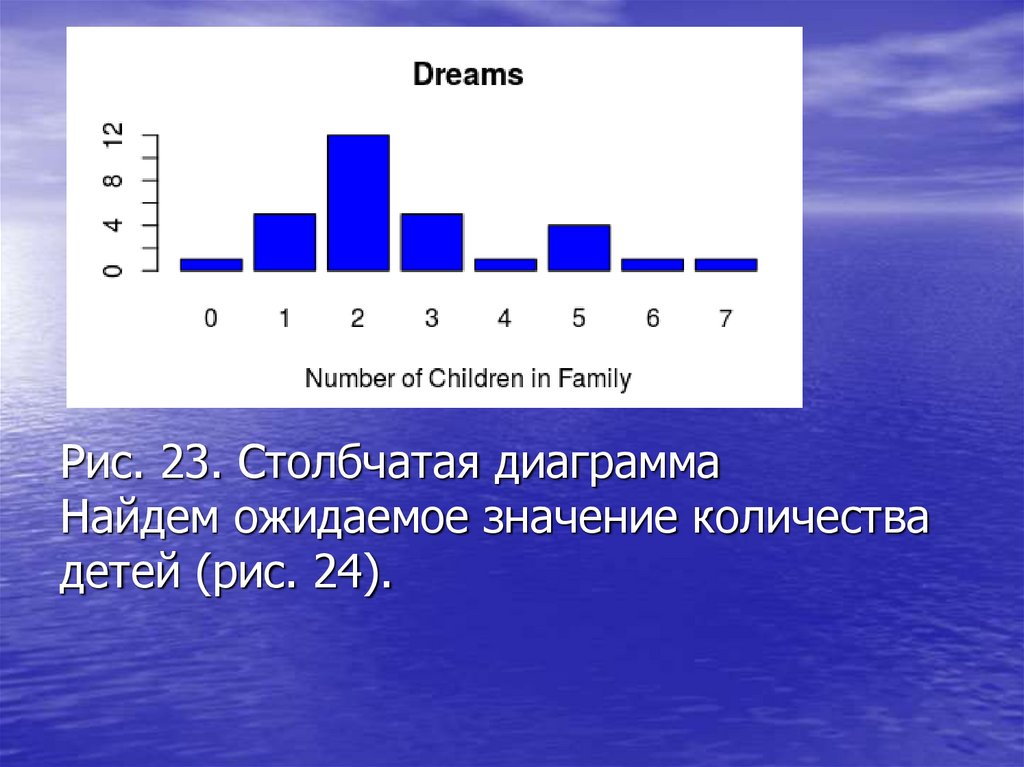
Рис. 23. Столбчатая диаграмма
Найдем ожидаемое значение количества
детей (рис. 24).

53.

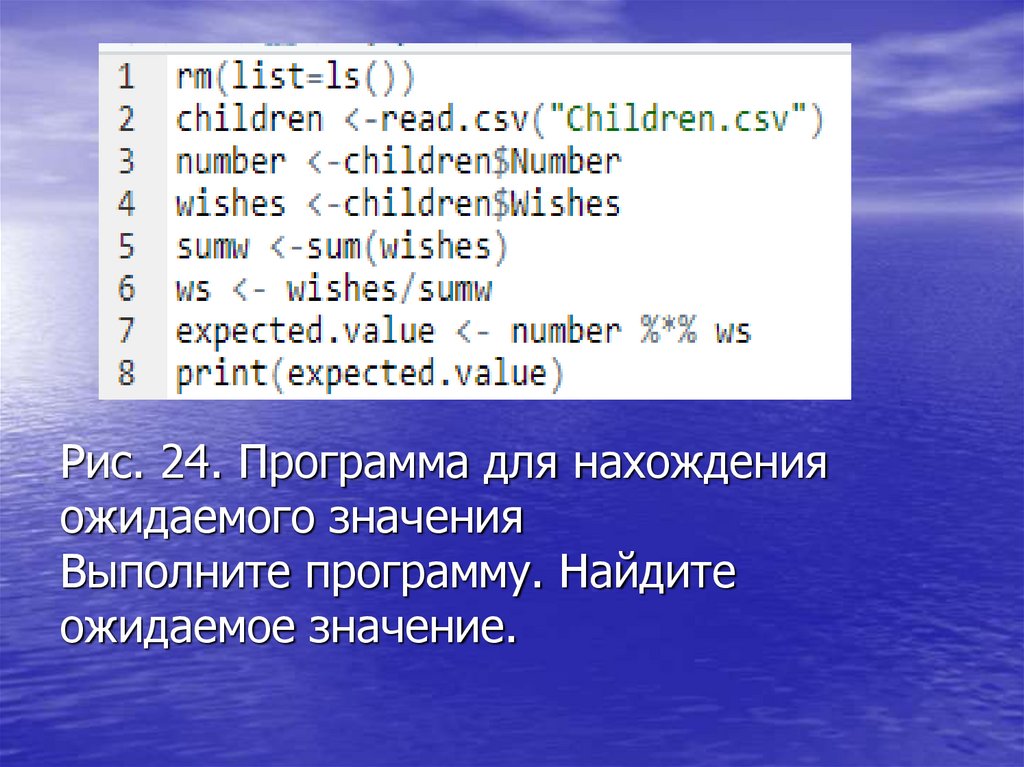
Рис. 24. Программа для нахождения
ожидаемого значения
Выполните программу. Найдите
ожидаемое значение.

54.

Обратите внимание выражение:
expected.value <- number %*% ws
Знаки %*% воспринимаются как единое
целое и обозначают вычисление
скалярного произведения.
Один знак * обозначает поэлементное
умножение векторов (массивов).
Теперь я покажу функцию, которая
позволяет сразу получить рассмотренные
ранее статистические характеристики
(рис. 25).

55.

Рис. 25. Функция для вычисления моды
Последняя строка сохраняет функцию
getmymode в файле getmymode.r.
Функция стала доступна в любой из
программ проекта.

56.

Рассмотрим применение этой функции к
числовым и категориальным данным (рис.
26).
Рис. 26. Нахождение моды для числовых
и категориальных данных.
Выполните!

57.

Корреляция
• Вопрос. Что характеризует
коэффициент корреляции?
• Каким образом мы его рассматриваем?
• Существуют различные подходы.

58.

•Коэффициент корреляции Пирсона
характеризует наличие линейной
зависимости между переменными.
•Пусть даны две выборки:
•Тогда:

59.

•Здесь:
- выборочные средние,
- выборочные дисперсии
Допущения:
- обе анализируемые переменные
распределены нормально;
- связь между анализируемыми
переменными линейна.
Пример. Он взят из [6]. Рассматриваются
данные о старых автомобилях (набор
данных mtcars [7]).

60.

•Рис. 27. Нахождение коэффициента
корреляции Пирсона двумя способами
Набор данных mtcars предустановлен –
сразу выводим его заголовок.

61.

•Устанавливаем пакет tidyverse и
библиотеку tidyverse. Удаляем из набора
данных столбцы vs (двигатель Vобразный – 0, рядный - 1) и am
(трансмиссия автоматическая – 0, ручная
– 1). В этих столбцах отображаются
категориальные данные.
•Внимание! %>% - данные передаются в
функцию!
•Находим корреляцию мощности в
лошадиных силах (hp) и расстояния в
милях на галлон США (mpg) горючего.

62.

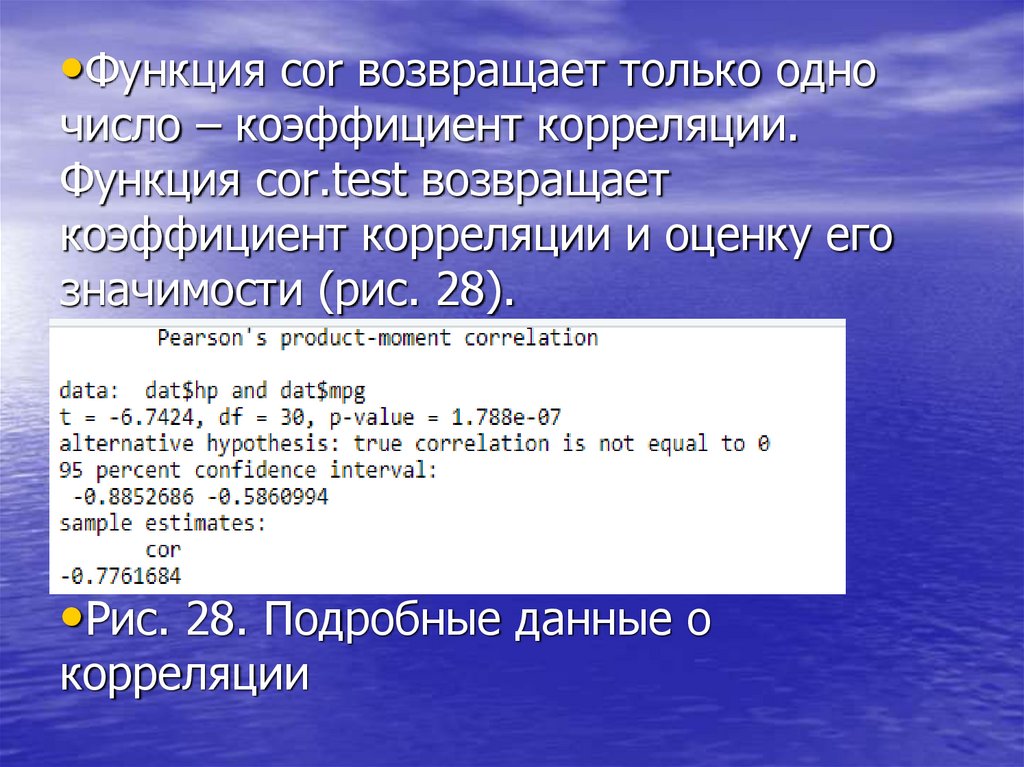
•Функция cor возвращает только одно
число – коэффициент корреляции.
Функция cor.test возвращает
коэффициент корреляции и оценку его
значимости (рис. 28).
•Рис. 28. Подробные данные о
корреляции

63.

•Для вычисления коэффициента
корреляции Спирмена используются
не сами значения, а их ранги.
•Пусть даны две выборки:
•Тогда коэффициент корреляции равен:

64.

•Здесь:
•При наличии совпадающих формулы
существенно усложняются.
•Найдем для тех же данных коэффициент
корреляции Спирмена (рис. 29).
•Рис. 29. Нахождение коэффициента
корреляции Спирмена двумя способами

65.

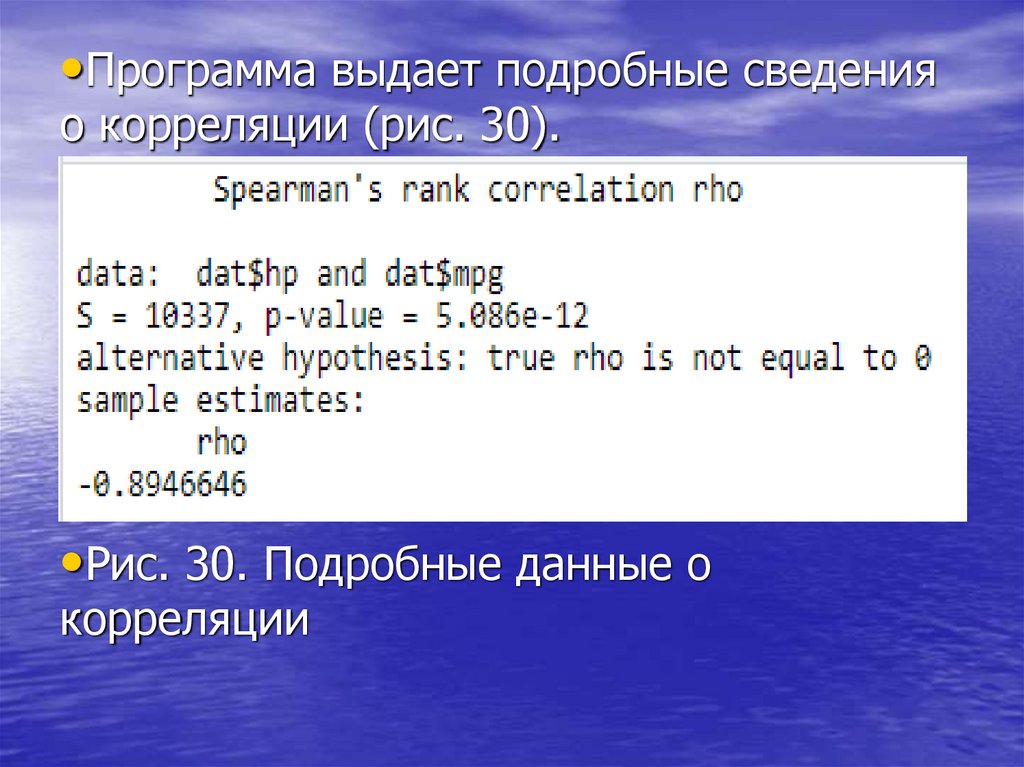
•Программа выдает подробные сведения
о корреляции (рис. 30).
•Рис. 30. Подробные данные о
корреляции

66.

•Коэффициент корреляции
Кендалла также является ранговым.
•Пусть даны две выборки:
•Тогда коэффициент корреляции равен:
•где

67.

•Найдем для тех же данных коффициент
корреляции Кендалла (рис. 31).
•Рис. 31. Нахождение коэффициента
корреляции Кендалла двумя способами
•Программа выдает подробные сведения
о корреляции (рис. 32).

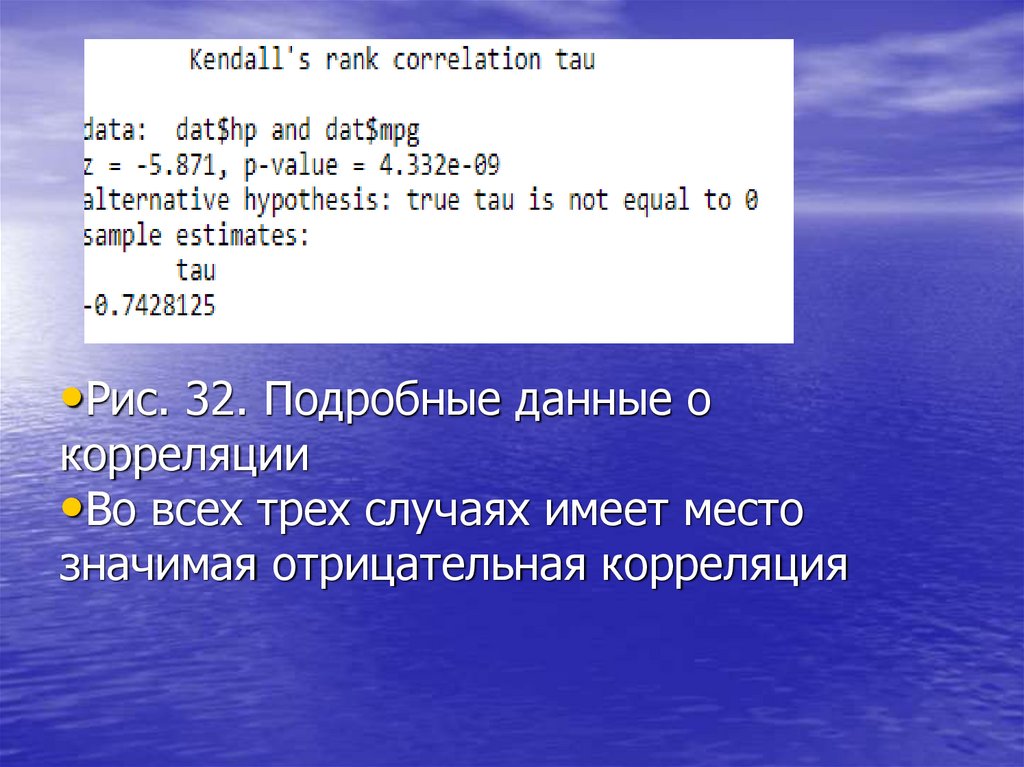
68.

•Рис. 32. Подробные данные о
корреляции
•Во всех трех случаях имеет место
значимая отрицательная корреляция

69.

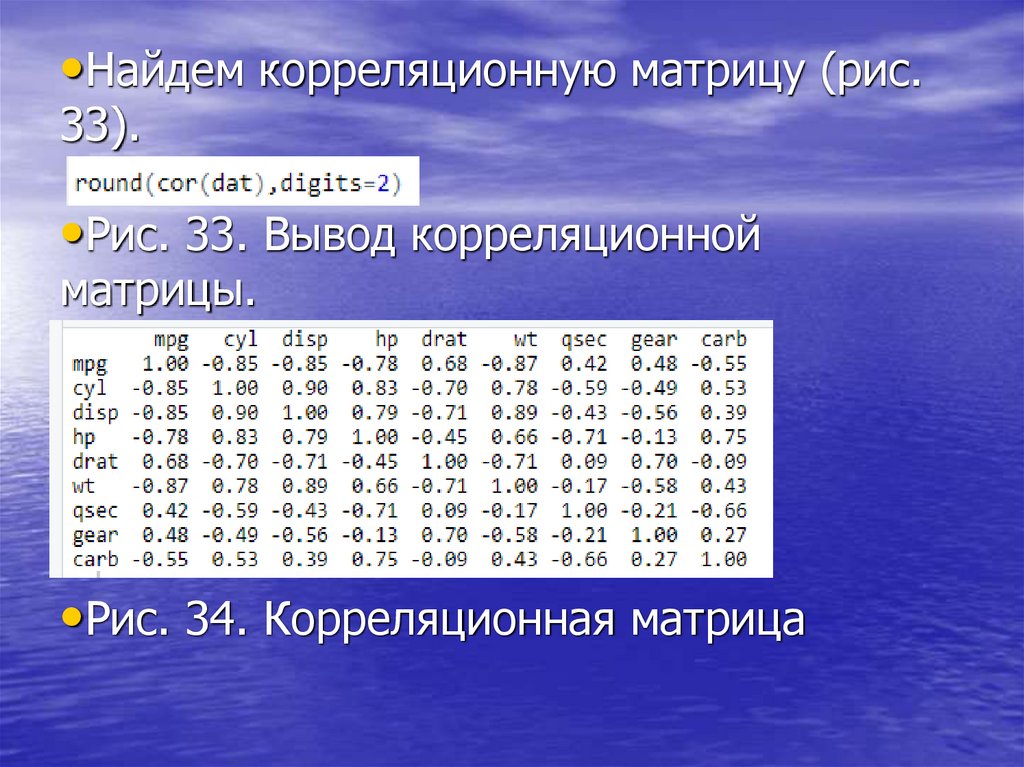
•Найдем корреляционную матрицу (рис.
33).
•Рис. 33. Вывод корреляционной
матрицы.
•Рис. 34. Корреляционная матрица

70.

•При нахождении корреляционной
матрицы по умолчанию используется
метод Пирсона. Можно использовать
метод Спирмена или Кендалла (рис. 29).
•Корреляционную матрицу можно
вывести ее в более наглядном виде (рис.
35).
•Рис. 35. Вывод корреляционной матрицы

71.

•Рис. 36. Корреляционная матрица
•Наглядно связь между исследуемыми
величинами можно представить с
помощью диаграммы рассеяния (рис. 37).

72.

•Рис. 37. Фрагмент кода для построения
диаграммы рассеяния
•Рис. 38. Диаграмма рассеяния

73.

• Ключевые термины:
• - коэффициент корреляции - correlation
coefficient;
• - корреляционная матрица - correlation
matrix;
• - диаграмма рассеяния – scatterplot.

74.

1. Сайт компании Логином. URL:
https://wiki.loginom.ru/articles/explorator
y-analysis.html
2. http://www.rdatamining.com/
3. http://www.r-tutor.com/
4. Брюс П. Практическая статистика для
специалистов Data Science: Пер. с англ. /
П. Брюс, Э. Брюс. – СПб.: БХВ-Петербург,
2018. – 304 с.

75.

5. https://ranalytics.blogspot.com/2011/11/r_08.html
6. https://statsandr.com/blog/correlationcoefficient-and-correlation-test-inr/#between-two-variables
7. https://stat.ethz.ch/R-manual/Rdevel/library/datasets/html/mtcars.html

English Русский Rules