Similar presentations:
Условия равновесия системы сил
1.
УСЛОВИЯ РАВНОВЕСИЯ СИСТЕМЫ СИЛДля равновесия системы сил необходимо и достаточно, чтобы главный
вектор и главный момент системы сил равнялись нулю:
n
F 0;
k 1
k
n
M ( F ) 0.
k 1
o
k
2.
УСЛОВИЯ РАВНОВЕСИЯ СИСТЕМЫ СИЛПримем точку О за начало координат.
В проекциях на координатные оси получаем:
n
F 0;
k 1
kx
n
n
M ( F ) 0;
k 1
x
k
n
F 0;
M ( F ) 0;
n
n
k 1
ky
F 0;
k 1
kz
k 1
y
k
M ( F ) 0.
k 1
z
k
Таким образом, для равновесия системы сил необходимо и достаточно,
чтобы сумма проекций всех сил системы на каждую из трёх взаимно
перпендикулярных осей равнялась нулю и сумма моментов всех сил
системы относительно каждой из этих осей равнялась нулю.
3.
УСЛОВИЯ РАВНОВЕСИЯ СИСТЕМЫ СИЛn
n
F 0;
kx
M ( F ) 0;
F 0;
ky
M ( F ) 0;
F 0;
M ( F ) 0.
k 1
n
k 1
n
k 1
kz
Рассмотрим пример.
k 1
n
k 1
n
k 1
x
y
z
k
k
k
4.
УСЛОВИЯ РАВНОВЕСИЯ СИСТЕМЫ СИЛn
F 0;
k 1
kx
n
n
M ( F ) 0;
k 1
x
k
n
F 0;
M ( F ) 0;
n
n
k 1
ky
F 0;
k 1
kz
Рассмотрим пример.
k 1
y
k
M ( F ) 0.
k 1
z
k
5.
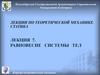
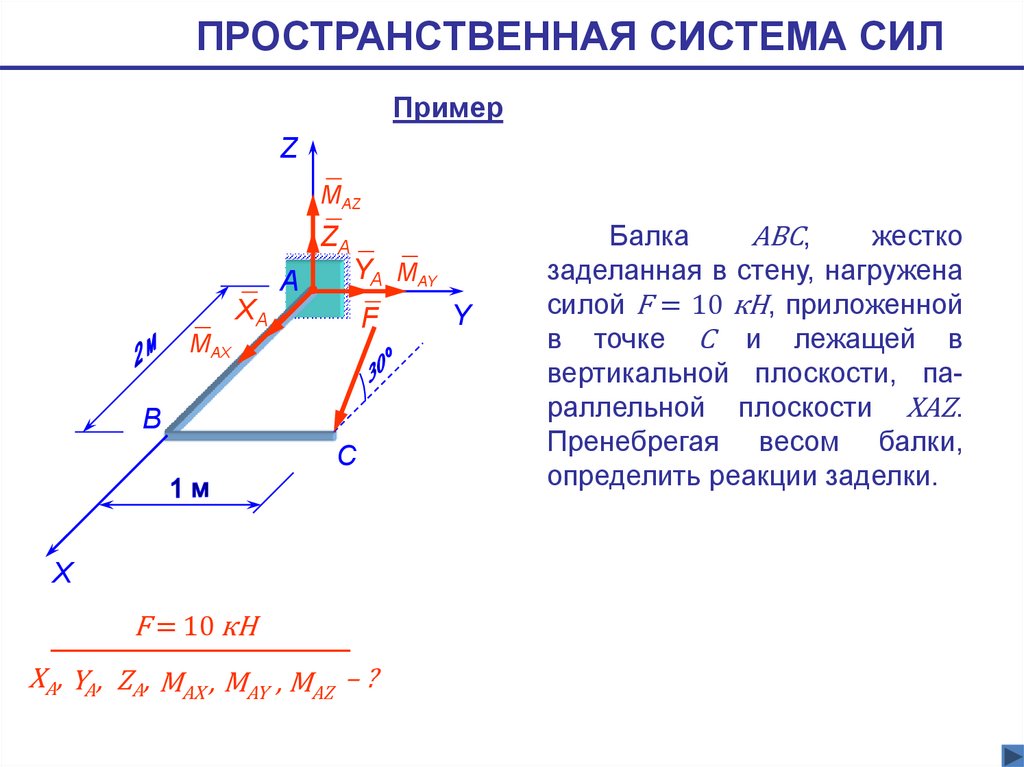
ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛПример
Z
A
F
B
C
X
Y
Балка
АВС,
жестко
заделанная в стену, нагружена
силой F = 10 кН, приложенной
в точке С и лежащей в
вертикальной плоскости, параллельной плоскости XAZ.
Пренебрегая весом балки,
определить реакции заделки.
6.
ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛПример
Z
A
F
B
C
X
F = 10 кН
Y
Балка
АВС,
жестко
заделанная в стену, нагружена
силой F = 10 кН, приложенной
в точке С и лежащей в
вертикальной плоскости, параллельной плоскости XAZ.
Пренебрегая весом балки,
определить реакции заделки.
7.
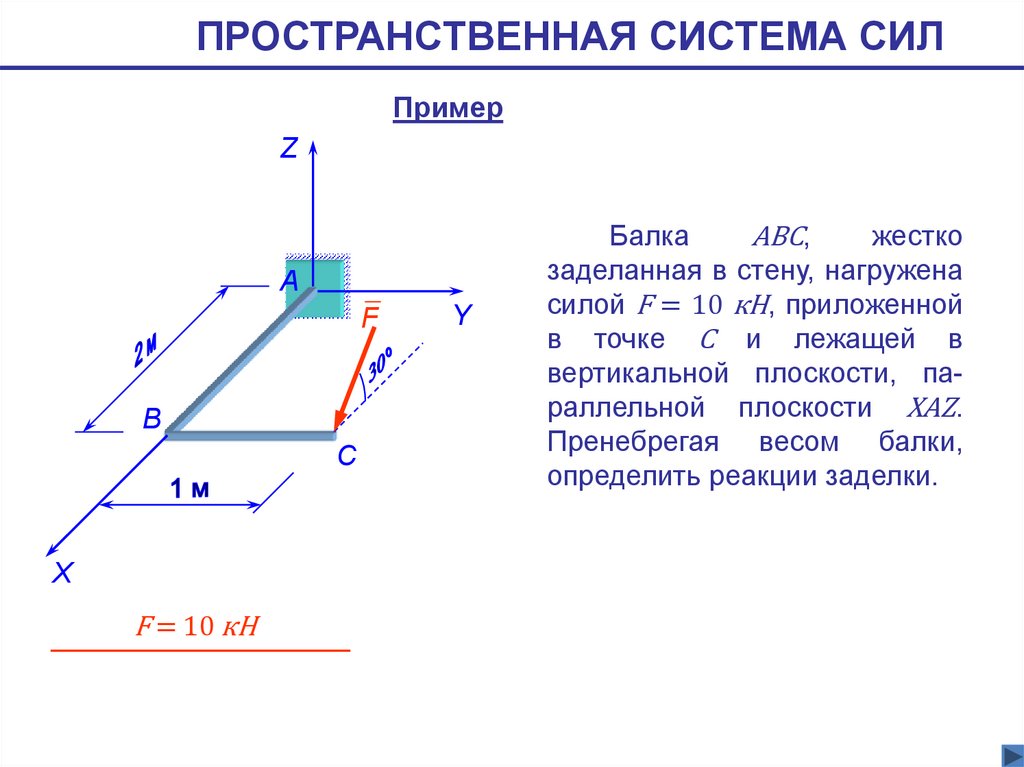
ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛПример
Z
ZA
A
YA
XA
F
B
C
X
F = 10 кН
Y
Балка
АВС,
жестко
заделанная в стену, нагружена
силой F = 10 кН, приложенной
в точке С и лежащей в
вертикальной плоскости, параллельной плоскости XAZ.
Пренебрегая весом балки,
определить реакции заделки.
8.
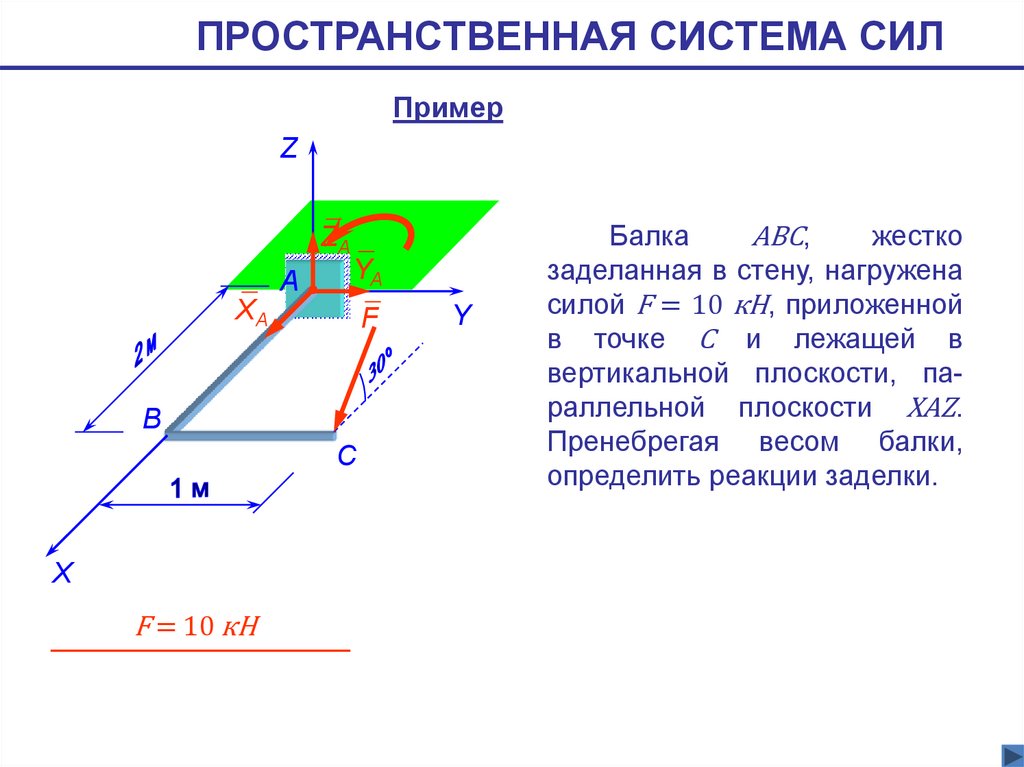
ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛПример
Z
ZA
A
YA
XA
F
B
C
X
F = 10 кН
Y
Балка
АВС,
жестко
заделанная в стену, нагружена
силой F = 10 кН, приложенной
в точке С и лежащей в
вертикальной плоскости, параллельной плоскости XAZ.
Пренебрегая весом балки,
определить реакции заделки.
9.
ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛПример
Z
ZA
A
YA
XA
F
B
C
X
F = 10 кН
Y
Балка
АВС,
жестко
заделанная в стену, нагружена
силой F = 10 кН, приложенной
в точке С и лежащей в
вертикальной плоскости, параллельной плоскости XAZ.
Пренебрегая весом балки,
определить реакции заделки.
10.
ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛПример
Z
ZA
A
YA
XA
F
B
C
X
F = 10 кН
Y
Балка
АВС,
жестко
заделанная в стену, нагружена
силой F = 10 кН, приложенной
в точке С и лежащей в
вертикальной плоскости, параллельной плоскости XAZ.
Пренебрегая весом балки,
определить реакции заделки.
11.
ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛПример
Z
ZA
A
YA
XA
F
B
C
X
F = 10 кН
Y
Балка
АВС,
жестко
заделанная в стену, нагружена
силой F = 10 кН, приложенной
в точке С и лежащей в
вертикальной плоскости, параллельной плоскости XAZ.
Пренебрегая весом балки,
определить реакции заделки.
12.
ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛПример
Z
ZA
A
YA
XA
F
B
C
X
F = 10 кН
Y
Балка
АВС,
жестко
заделанная в стену, нагружена
силой F = 10 кН, приложенной
в точке С и лежащей в
вертикальной плоскости, параллельной плоскости XAZ.
Пренебрегая весом балки,
определить реакции заделки.
13.
ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛПример
Z
ZA
A
YA
XA
F
B
C
X
F = 10 кН
Y
Балка
АВС,
жестко
заделанная в стену, нагружена
силой F = 10 кН, приложенной
в точке С и лежащей в
вертикальной плоскости, параллельной плоскости XAZ.
Пренебрегая весом балки,
определить реакции заделки.
14.
ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛПример
Z
МAZ
ZA
A
МAХ
YA МAY
XA
F
B
C
X
F = 10 кН
Y
Балка
АВС,
жестко
заделанная в стену, нагружена
силой F = 10 кН, приложенной
в точке С и лежащей в
вертикальной плоскости, параллельной плоскости XAZ.
Пренебрегая весом балки,
определить реакции заделки.
15.
ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛПример
Z
МAZ
ZA
A
МAХ
YA МAY
XA
F
B
C
X
F = 10 кН
XA, YA, ZA, МAХ , МAY , МAZ – ?
Y
Балка
АВС,
жестко
заделанная в стену, нагружена
силой F = 10 кН, приложенной
в точке С и лежащей в
вертикальной плоскости, параллельной плоскости XAZ.
Пренебрегая весом балки,
определить реакции заделки.
16.
ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛПример
Z
Решение
МAZ
ZA
A
МAХ
YA МAY
XA
F
B
C
X
F = 10 кН
XA, YA, ZA, МAХ , МAY , МAZ – ?
Y
Балка
АВС,
жестко
заделанная в стену, нагружена
силой F = 10 кН, приложенной
в точке С и лежащей в
вертикальной плоскости, параллельной плоскости XAZ.
Пренебрегая весом балки,
определить реакции заделки.
17.
ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛПример
Z
Решение
МAZ
ZA
YA МAY
A
МAХ
XA
F
F3
B
F1
C
X
F = 10 кН
XA, YA, ZA, МAХ , МAY , МAZ – ?
Y
18.
ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛПример
Z
Решение
МAZ
ZA
YA МAY
A
МAХ
XA
F
F3
B
F1
C
X
F = 10 кН
XA, YA, ZA, МAХ , МAY , МAZ – ?
Y
19.
ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛПример
Z
Решение
МAZ
F1 = F cos 300 = 10 √3/2 = 5√3 (кН);
F3 = F sin 300 = 10 ·1/2 = 5 (кН).
ZA
YA МAY
A
МAХ
XA
F
F3
B
F1
C
X
F = 10 кН
XA, YA, ZA, МAХ , МAY , МAZ – ?
Y
20.
ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛПример
Z
Решение
МAZ
F1 = F cos 300 = 10 √3/2 = 5√3 (кН);
F3 = F sin 300 = 10 ·1/2 = 5 (кН).
ZA
YA МAY
A
МAХ
XA
F
Y
∑ Fkx= 0 : XA + F1 = 0 => XA = –F1 = –5√3 (кН)
F3
B
F1
C
X
F = 10 кН
XA, YA, ZA, МAХ , МAY , МAZ – ?
21.
ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛПример
Z
Решение
МAZ
F1 = F cos 300 = 10 √3/2 = 5√3 (кН);
F3 = F sin 300 = 10 ·1/2 = 5 (кН).
ZA
YA МAY
A
МAХ
XA
F
F3
B
F1
C
X
F = 10 кН
XA, YA, ZA, МAХ , МAY , МAZ – ?
Y
∑ Fkx= 0 : XA + F1 = 0 => XA = –F1 = –5√3 (кН)
∑ Fky= 0 : YA = 0
22.
ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛПример
Z
Решение
МAZ
F1 = F cos 300 = 10 √3/2 = 5√3 (кН);
F3 = F sin 300 = 10 ·1/2 = 5 (кН).
ZA
YA МAY
A
МAХ
XA
F
F3
B
F1
C
X
F = 10 кН
XA, YA, ZA, МAХ , МAY , МAZ – ?
Y
∑ Fkx= 0 : XA + F1 = 0 => XA = –F1 = –5√3 (кН)
∑ Fky= 0 : YA = 0
∑ Fkx= 0 : ZA – F3 = 0 => XA = F3 = 5 (кН)
23.
ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛПример
Z
Решение
МAZ
F1 = F cos 300 = 10 √3/2 = 5√3 (кН);
F3 = F sin 300 = 10 ·1/2 = 5 (кН).
ZA
YA МAY
A
МAХ
XA
Y
F
F3
B
F1
C
∑ Fkx= 0 : XA + F1 = 0 => XA = –F1 = –5√3 (кН)
∑ Fky= 0 : YA = 0
∑ Fkx= 0 : ZA – F3 = 0 => XA = F3 = 5 (кН)
∑ MAX(Fk) = 0 : MAX – F3∙1= 0 => MAX = 5 (кН м)
X
F = 10 кН
XA, YA, ZA, МAХ , МAY , МAZ – ?
24.
ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛПример
Z
Решение
МAZ
F1 = F cos 300 = 10 √3/2 = 5√3 (кН);
F3 = F sin 300 = 10 ·1/2 = 5 (кН).
ZA
YA МAY
A
МAХ
XA
Y
F
F3
B
F1
C
∑ Fkx= 0 : XA + F1 = 0 => XA = –F1 = –5√3 (кН)
∑ Fky= 0 : YA = 0
∑ Fkx= 0 : ZA – F3 = 0 => XA = F3 = 5 (кН)
∑ MAX(Fk) = 0 : MAX – F3∙1= 0 => MAX = 5 (кН м)
∑ MAY(Fk) = 0 : MAY + F3∙2= 0 => MAY = – 10 (кН м)
X
F = 10 кН
XA, YA, ZA, МAХ , МAY , МAZ – ?
25.
ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛПример
Z
Решение
МAZ
F1 = F cos 300 = 10 √3/2 = 5√3 (кН);
F3 = F sin 300 = 10 ·1/2 = 5 (кН).
ZA
YA МAY
A
МAХ
XA
Y
F
F3
B
F1
C
∑ Fkx= 0 : XA + F1 = 0 => XA = –F1 = –5√3 (кН)
∑ Fky= 0 : YA = 0
∑ Fkx= 0 : ZA – F3 = 0 => XA = F3 = 5 (кН)
∑ MAX(Fk) = 0 : MAX – F3∙1= 0 => MAX = 5 (кН м)
∑ MAY(Fk) = 0 : MAY + F3∙2= 0 => MAY = – 10 (кН м)
∑ MAZ(Fk) = 0 : MAZ – F1∙1= 0 => MAZ = 5√3 (кН м)
X
F = 10 кН
XA, YA, ZA, МAХ , МAY , МAZ – ?





















 physics
physics