Similar presentations:
Конус
1.
2. Содержание
ОпределениеОсновные понятия
Виды конусов
Основные формулы
Сечение конуса плоскостью
Задача
Примеры из окружающего мира
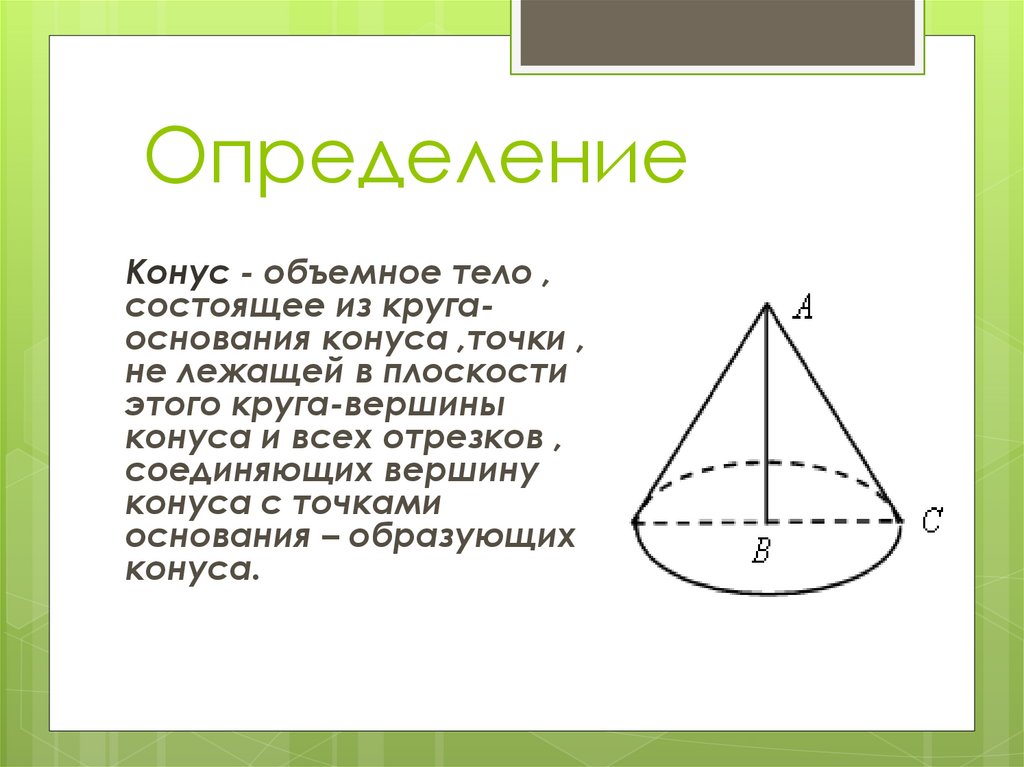
3. Определение
Конус - объемное тело ,состоящее из кругаоснования конуса ,точки ,
не лежащей в плоскости
этого круга-вершины
конуса и всех отрезков ,
соединяющих вершину
конуса с точками
основания – образующих
конуса.
4.
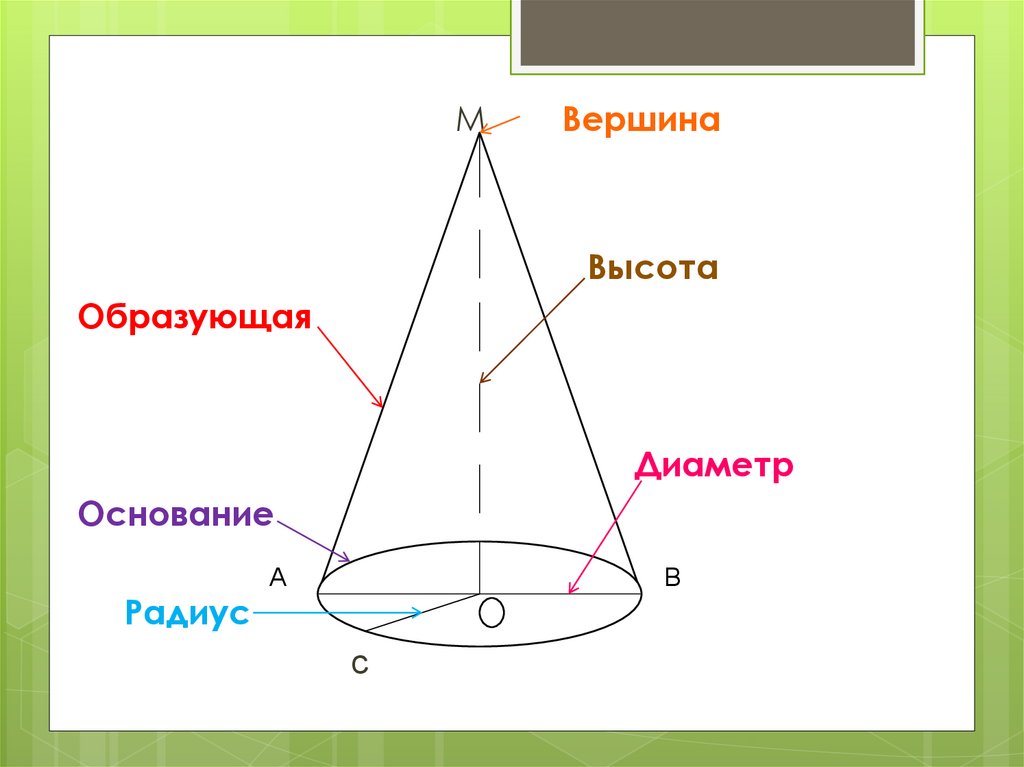
МВершина
Высота
Образующая
Диаметр
Основание
Радиус
А
В
с
5. Основные понятия
Образующая конуса - это отрезок, соединяющий вершину конуса иточку на окружности основания.
Высота конуса - это перпендикуляр ,проведённый из вершины конуса
на плоскость основания.
Ось симметрии - это прямая , проходящая через вершину и центр
основания прямого конуса.
Радиус конуса - это отрезок , соединяющий центр основания с
точкой на окружности.
Диаметр конуса - это отрезок , соединяющий две точки окружности
основания , проходящий через центр.
Хорда – это отрезок, соединяющий две точки окружности основания
не проходящий через центр.
Боковая поверхность конуса состоит из множества всех
образующих.
6. Виды конусов
Прямой конусНаклонный конус
Усеченный конус
7. Прямой конус
Прямой конус -объемное тело,образуемое вращением
прямоугольного треугольника около
одного из катетов или вращением
равнобедренного треугольника
вокруг оси симметрии ,
Свойства:
1.Высота , проведённая из вершины,
попадает в центр основания.
2. Образующие равны.
3. Образующие наклонены к плоскости
основания под одинаковым углом.
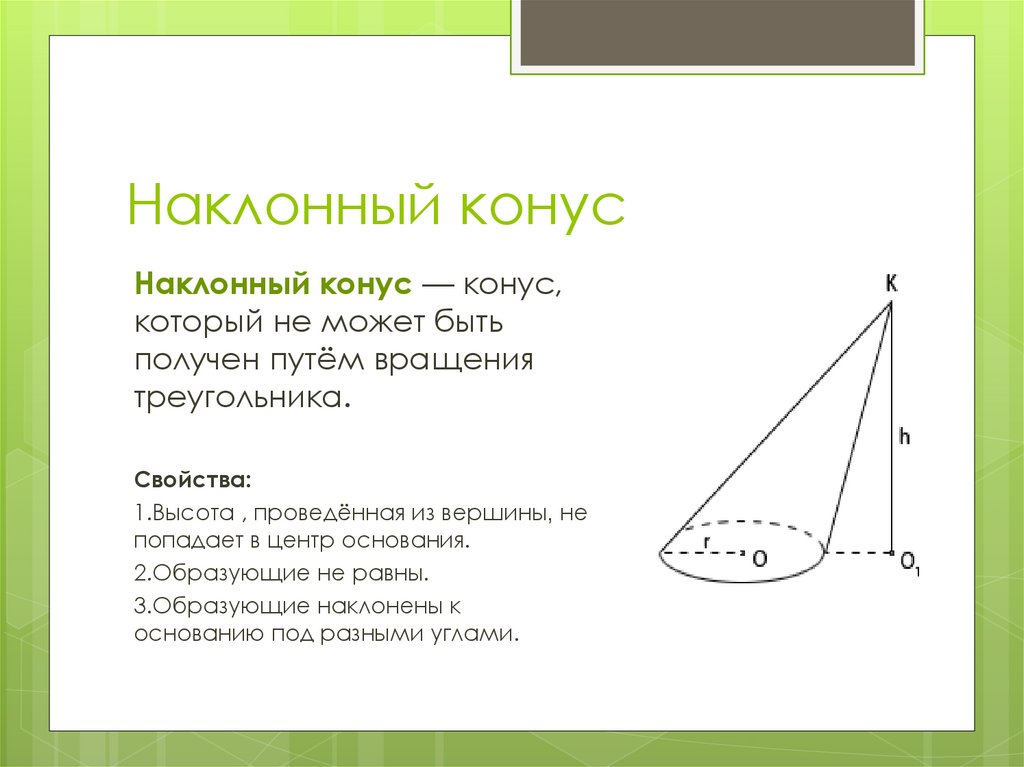
8. Наклонный конус
Наклонный конус — конус,который не может быть
получен путём вращения
треугольника.
Свойства:
1.Высота , проведённая из вершины, не
попадает в центр основания.
2.Образующие не равны.
3.Образующие наклонены к
основанию под разными углами.
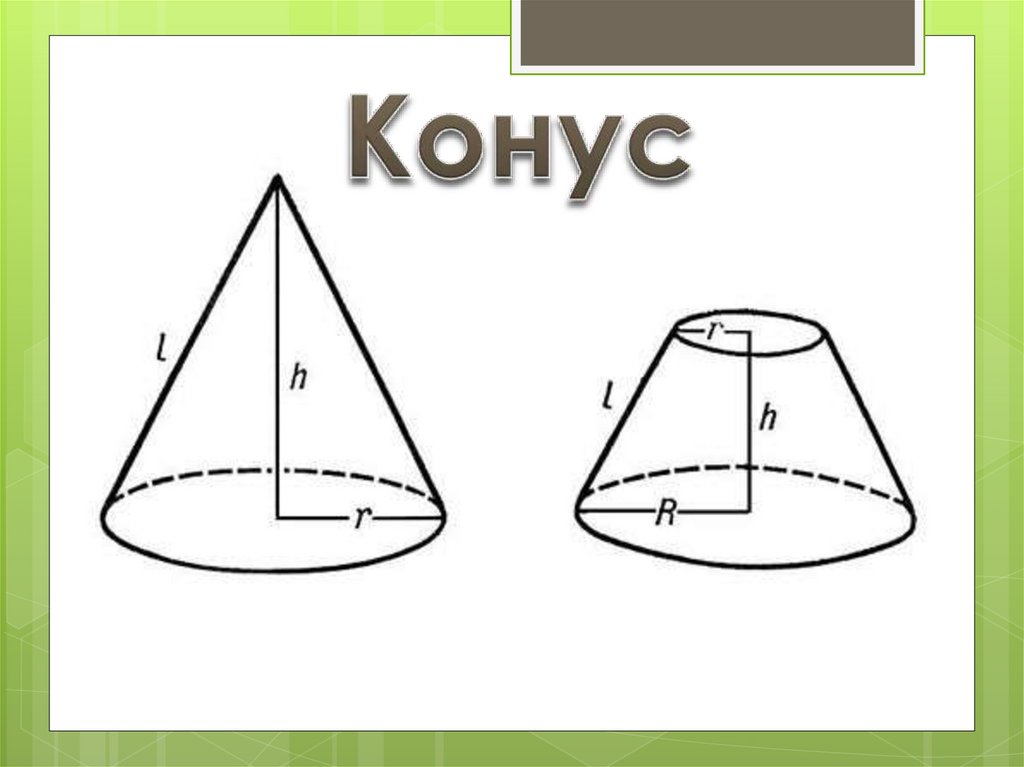
9. Усеченный конус
Если плоскость,параллельная основанию
пересекает конус, то
получаются два тела.
Вверху получается меньший
конус, подобный данному.
Оставшаяся часть
называется усеченным
конусом.
10. Основные формулы
11. Сечения конуса плоскостью
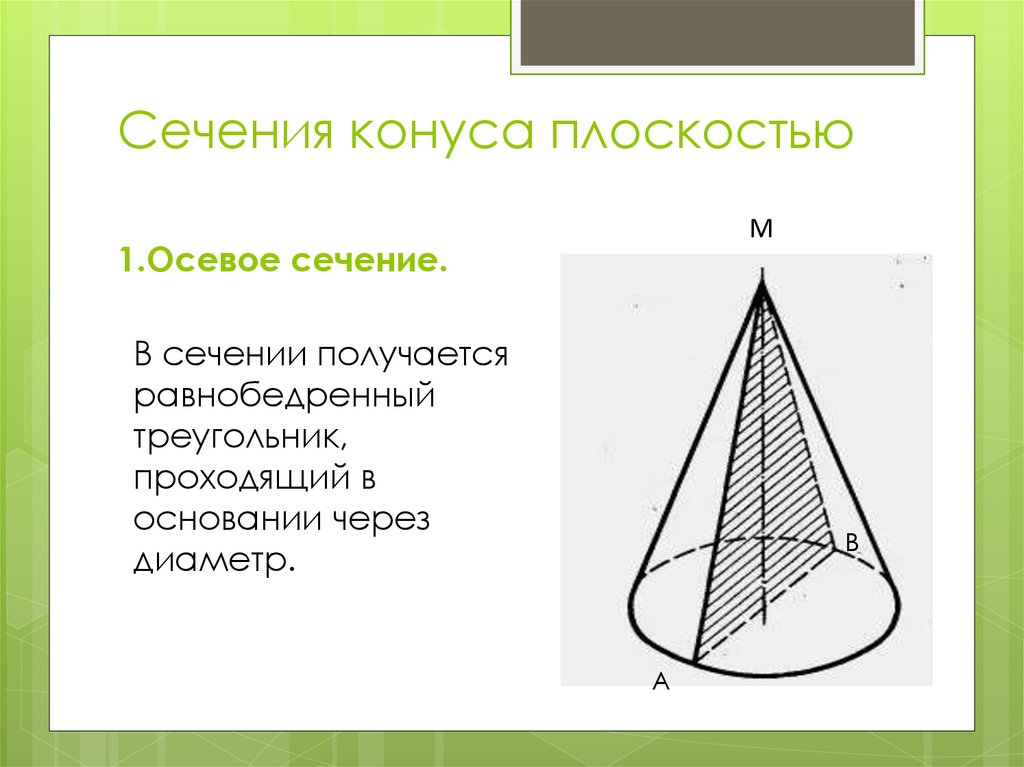
М1.Осевое сечение.
В сечении получается
равнобедренный
треугольник,
проходящий в
основании через
диаметр.
B
A
12. Сечения конуса плоскостью
2. Сечениепроходящее через
вершину и хорду
.
В сечении
получается
равнобедренный
треугольник.
13. Сечения конуса плоскостью
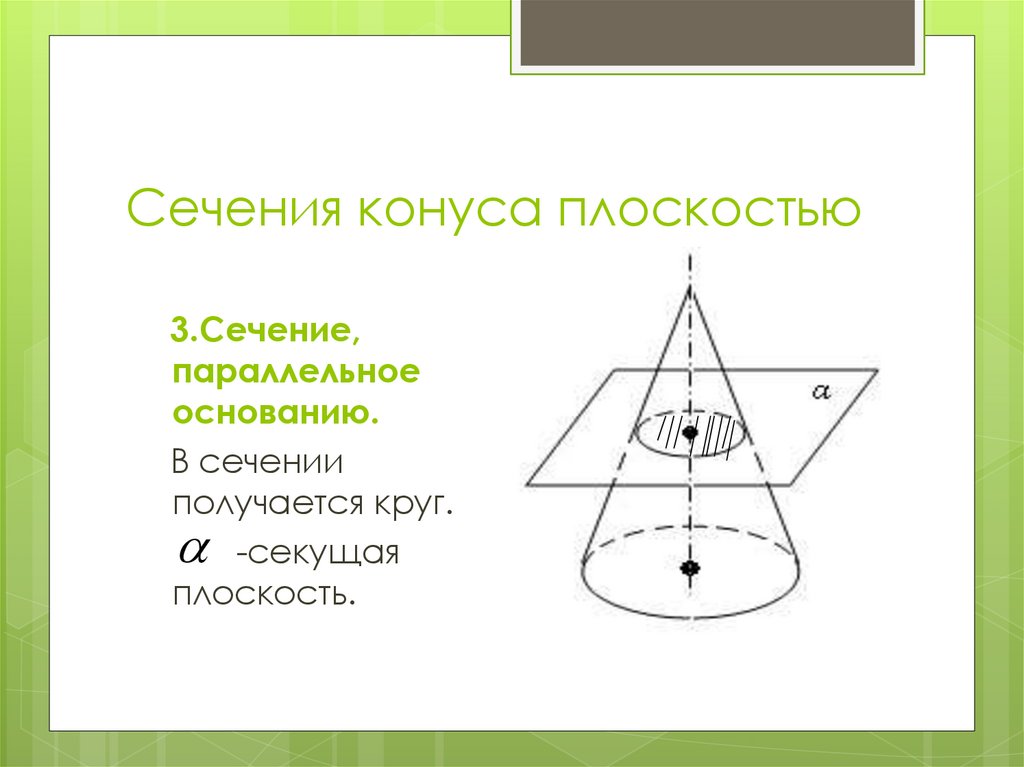
3.Сечение,параллельное
основанию.
В сечении
получается круг.
-секущая
плоскость.
14. Задача.
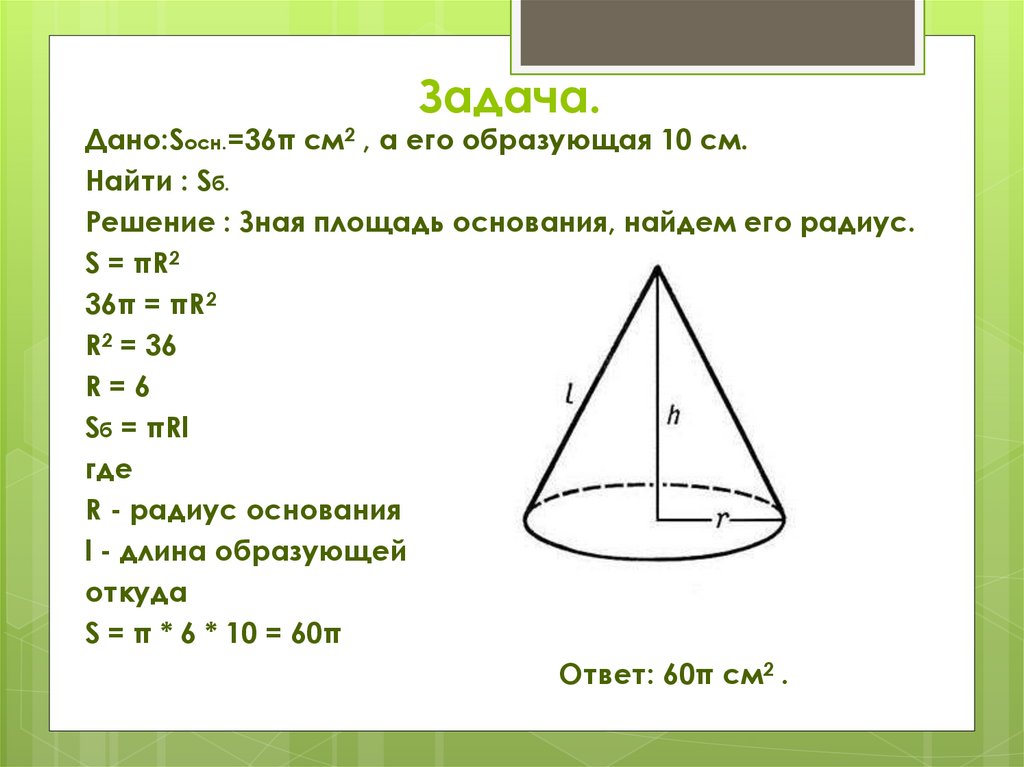
Дано:Sосн.=36π см2 , а его образующая 10 см.Найти : Sб.
Решение : Зная площадь основания, найдем его радиус.
S = πR2
36π = πR2
R2 = 36
R=6
Sб = πRl
где
R - радиус основания
l - длина образующей
откуда
S = π * 6 * 10 = 60π
Ответ: 60π см2 .








 mathematics
mathematics








