Similar presentations:
Правило сложения дисперсий
1. СТАТИСТИКА
2.
КафедраСтатистики, эконометрики и
оценки рисков
Лектор:
Зав.каф. д.э.н., проф.
Ниворожкина Людмила
Ивановна
3.
Вариация признаков, как правило,обусловлена влиянием различных
факторов. Если совокупность разбить
на группы по факторному признаку, то
это окажет определенное влияние на
значение вариации признака в группах.
Выявить долю вариации,
определяемую теми или иными
факторами, можно разделяя всю
совокупность на группы по фактору,
влияние которого исследуется.
4.
Чаще всего для этих целейиспользуются показатели вариации для
сгруппированных данных. В этом
случае выделяют три вида дисперсий:
общую дисперсию;
внутригрупповую дисперсию,
межгрупповую дисперсию.
5.
Общая дисперсия измеряет вариациюпризнака во всей совокупности под
влиянием всех факторов.
Внутригрупповая дисперсия измеряет
вариацию признака внутри группы.
Межгрупповая дисперсия измеряет
вариацию групповых средних
относительно общей средней.
6.
Рассмотрим простейший случай,когда исходная совокупность
делится на группы по одному
признаку-фактору.
Допустим, имеется распределение
исходной совокупности,
представленное в следующей
таблице:
7.
Значение Число единиц в j -й группе Итогопризнака
1
2
x1
f1
s1
x2
f2
s2
…
…
…
xk
fk
sk
Итого
N1
N2
…
…
m
t1
f1 + s1 + ... + t1 = n1
…
…
t2
f 2 + s2 + ... + t 2 = n2
…
…
tk
f k + sk + ... + t k = nk
Nm
N
…
…
8.
Сначала вычислим m частных средних,то есть среднее значение признака в
каждой группе:
x1 =
k
å xi f i
i =1
N1 ,
9.
x2 =…
k
å xi si
i =1
N2
,
10.
x,
x
,...,
x
1
2
m
На основе частных средних
определяем общую среднюю по формуле
xобщ. =
m
å xj N j
j =1
N
,
где
m
k
N = å N j = å ni
j =1
i =1 .
11.
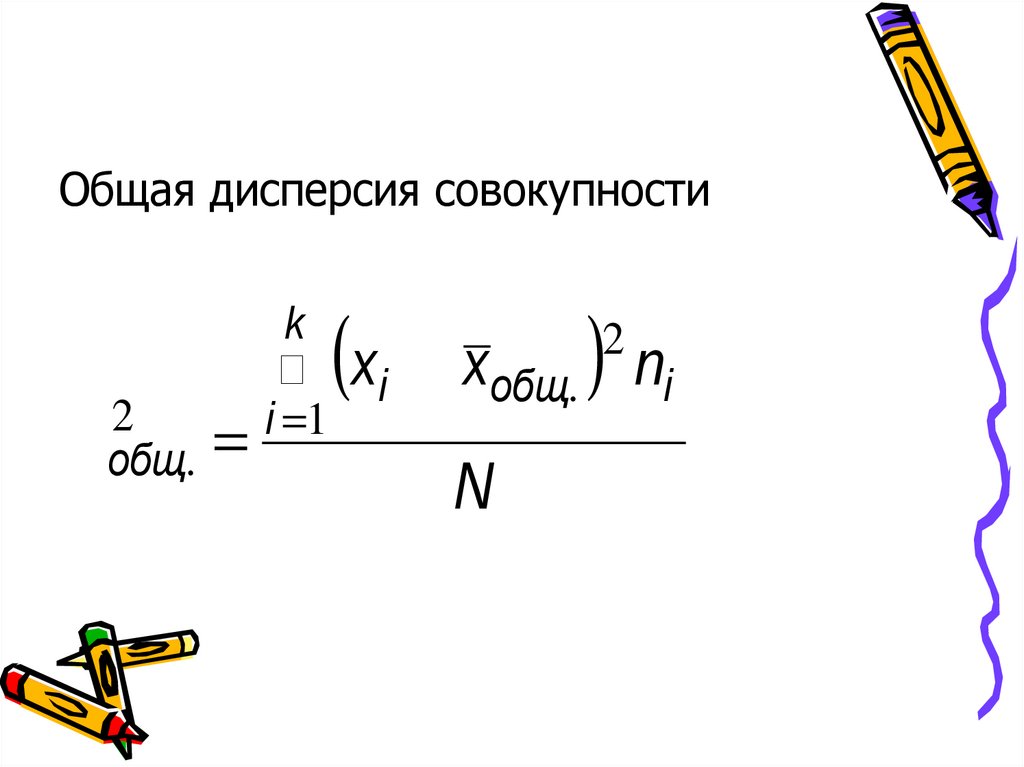
Общая дисперсия совокупности2
s общ. =
(
)
k
2
å xi - xобщ. ni
i =1
N
12.
Общая дисперсия отражает вариациюпризнака за счет всех условий (факторов),
действующих в совокупности.
13.
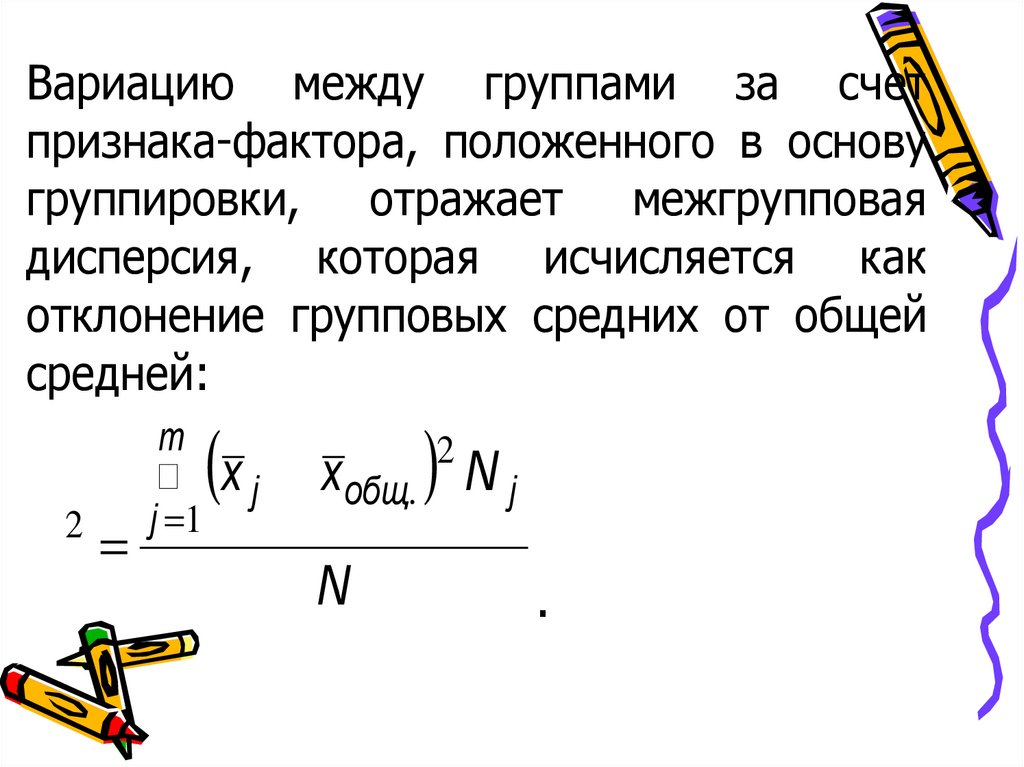
Вариацию между группами за счетпризнака-фактора, положенного в основу
группировки, отражает межгрупповая
дисперсия, которая исчисляется как
отклонение групповых средних от общей
средней:
d =
2
(
)
m
2
å x j - xобщ. N j
j =1
N
.
14.
Вариациювнутри
каждой
группы
изучаемой совокупности отражает частная
групповая дисперсия, которая исчисляется
как средний квадрат отклонений значений
признака
x от частной средней
xj
15.
k2
(
)
x
x
å i
1 fi
2 i =1
s1 =
N1
k
2
å ( xi - x2 ) si
2 i =1
s2 =
N2
…….
k
2
å ( xi - xm ) t i
2
i
=
1
sm =
Nm
16.
В общем виде частную дисперсию запишемтак:
k
2
å xi - x j N ij
2 i =1
sj =
Nj
(
где
Nij
)
- частоты от i = 1,2,..., k в каждой
j группе.
17.
Так как изучаемая совокупностьразбита на несколько групп, то для
всей совокупности внутригрупповую
вариацию
будет
выражать
внутригрупповая дисперсия, которая
рассчитывается
как
средняя
арифметическая
из
групповых
дисперсий:
18.
s =2
m 2
å sjNj
j =1
N
19.
Существует закон, связывающий три видадисперсии:
Общая дисперсия равна сумме
межгрупповой дисперсии и средней из
внутригрупповых дисперсий:
s =d +s
2
2
2
20.
Логика этого закона проста: общаядисперсия,
возникающая
под
воздействием
всех
факторов,
формируется
из
дисперсии,
возникающей
за
счет
фактора
группировки
и
дисперсии,
возникающей под воздействием всех
прочих факторов.
Автор
этого
закона
немецкий
статистик Вильгельм Лексис (1837 –
1914).
21.
С помощью закона сложениядисперсий можно оценить удельный
вес факторов, лежащих в основе
группировки, во всей совокупности
факторов, воздействующих на
результативный признак.
22.
Для этого применяетсякоэффициент
детерминации, который рассчитывается
как отношение межгрупповой (факторной)
дисперсии
к
общей
дисперсии
результативного признака:
d
h = 2
s
2
2
.
23.
Корень квадратный из коэффициентадетерминации называют эмпирическим
корреляционным отношением:
2
d
h= 2
s .
24.
Эмпирическоекорреляционное
отношение показывает какую часть общей
колеблемости результативного признака
определяет изучаемый фактор, то есть
характеризует влияние группировочного
признака на результативный признак.
Этот показатель принимает значения в
интервале [0,1]. Если связь отсутствует,
то h = 0. В этом случае дисперсия
групповых средних равна нулю
(d2 = 0), то есть все групповые средние
равны между собой и межгрупповой
вариации нет.
25.
Этоозначает,
что
группировочный
признак
не
влияет
на
вариацию
исследуемого признака х. Если связь
функциональная, то = 1. В этом случае
дисперсия групповых средних равна
общей дисперсии ( 2 = 2), то есть не
будет внутригрупповой дисперсии. Это
означает, что группировочный признак
полностью
определяет
вариацию
изучаемого признака а влияние прочих
факторных
признаков
равно
нулю.
Промежуточные значения оцениваются
по степени их близости к предельным.
26.
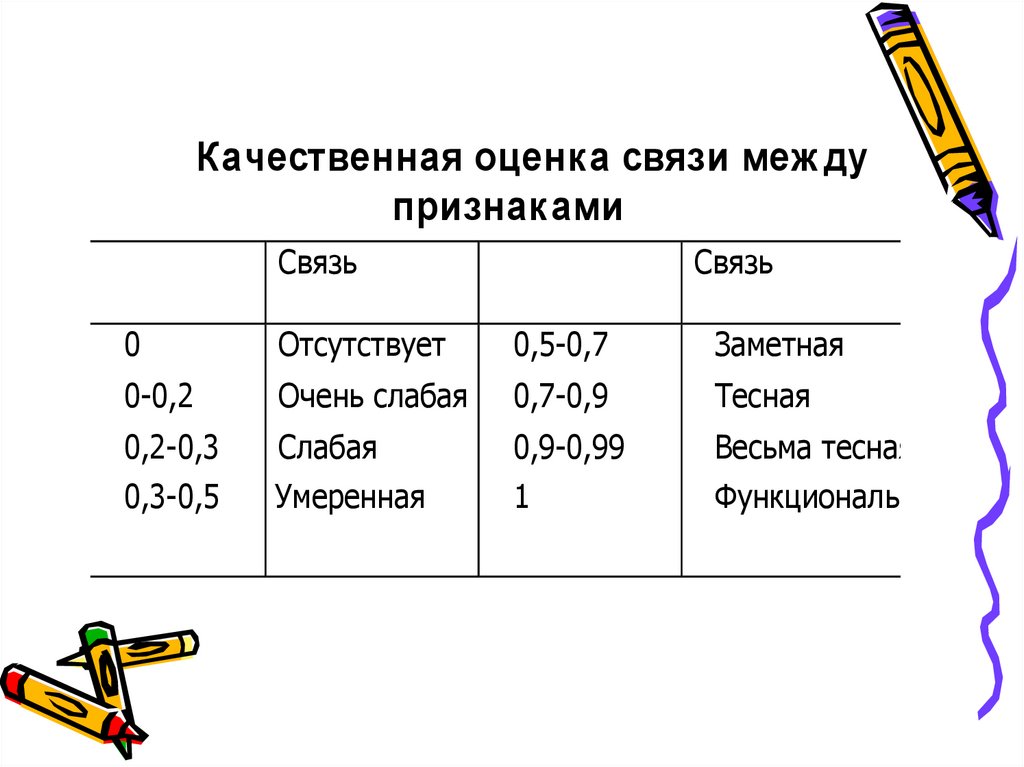
Качественная оценка связи меж дупризнаками
Связь
h
Связь
0
Отсутствует
0,5-0,7
Заметная
0-0,2
Очень слабая
0,7-0,9
Тесная
0,2-0,3
Слабая
0,9-0,99
Весьма тесная
0,3-0,5
Умеренная
1
Функциональная
h
27.
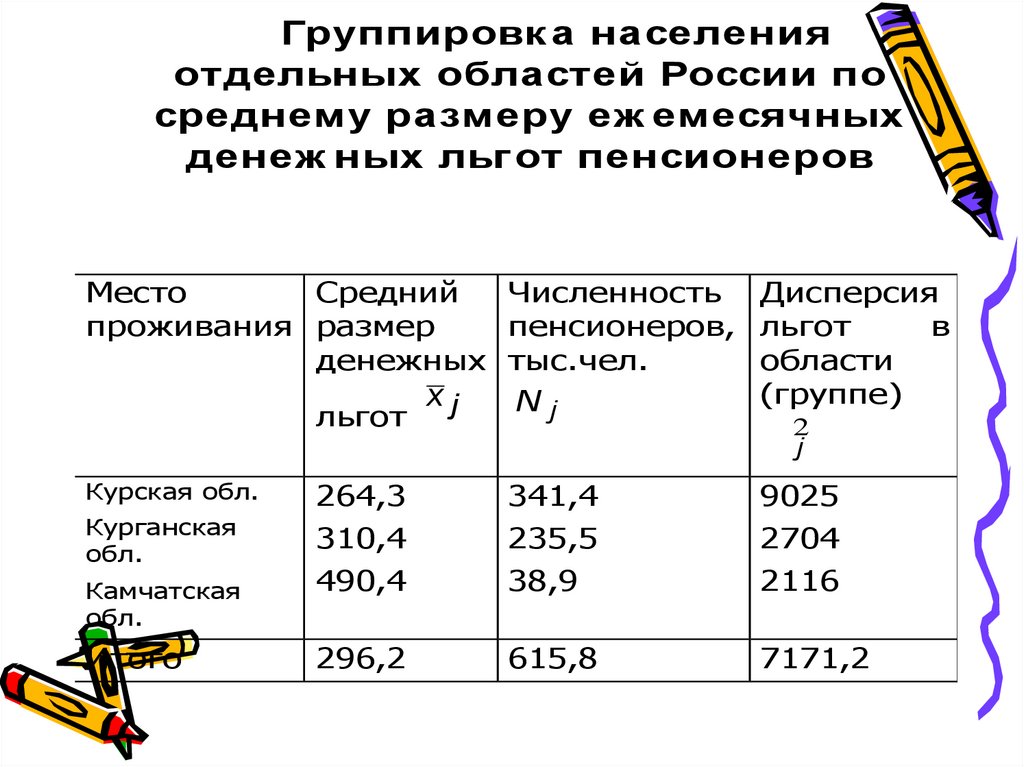
Группировк а населенияотдельных областей России по
среднему размеру еж емесячных
денеж ных льг от пенсионеров
Место
Средний
Численность Дисперсия
проживания размер
пенсионеров, льгот
в
денежных тыс.чел.
области
(группе)
xj
Nj
льгот
2
sj
Курская обл.
264,3
341,4
9025
Курганская
обл.
310,4
235,5
2704
490,4
38,9
2116
296,2
615,8
7171,2
Камчатская
обл.
Итого
28.
Сначала найдем средний размер льгот потрем областям в целом:
å xjN j
j
264,3 å341,4 + 310,4 å235,5 + 490,4 å38,9
xобщ. =
=
= 296,2
615,8
åNj
j
29.
Вариация льгот по отдельным областям,местах
в
различием
обусловленная
проживания пенсионеров, характеризуется
межгрупповой дисперсией:
å (x - x ) N
m
d2 =
j =1
2
общ.
j
N
2
2
(
264,3 - 296,2) å341,5 + (310,4 - 296,2) å235,5
=
615,8
(490,4 - 296,2) å38,9 = 2976,1
2
+
j
615,8
30.
Средняя из групповых дисперсий даетобобщающую характеристику случайной
вариации, обусловленную отдельными
факторами, кроме места проживания
пенсионеров
(например,
характером
занятости, стажем работы и т.п.):
31.
Вариация льгот в изучаемых областяхРоссии, обусловленная влиянием всех
факторов, вместе взятых, определяется
общей дисперсией:
s = d + s = 2976,1 + 6171,2 = 9147,3
2
2
2
отсюда
h =
2
d
2
2
s общ.
2976,1
=
= 0,325
9147,3
32.
Полученный коэффициент детерминациипоказывает, что дисперсия льгот зависит от
места проживания пенсионеров на 32,5 %.
Остальные
67,5%
определяются
множеством других неучтенных факторов.
h = h = 0,325 = 0,57
2
33.
Полученноезначение
эмпирического
корреляционного отношения позволяет
утверждать, что существует заметная связь
между местом проживания пенсионеров и
размером льгот.
34.
Вариация альтернативного признак аСреди
признаков,
изучаемых
статистикой,
есть
такие,
которые
принимают
лишь
два
взаимно
исключающих
значения.
Это
–
альтернативные признаки. Им придается
соответственно два значения: 1 и 0.
Частостью варианта 1 (она обозначается p
) является доля единиц, обладающих
данным признаков, в общей численности
совокупности.
35.
1p
=
q
Разность
является частостью
варианта 0. Таким образом:
xi wi
1
p
0
q
Средняя арифметическая альтернативного
признака
1 åp + 0 åq
x=
= p.
p+q
36.
Дисперсия альтернативного признака(
1 - p ) p + (0 - p ) q q p + p q
s =
=
= pq
2
2
2
p+q
2
2
p+q
,
то есть дисперсия альтернативного
признака равна произведению доли
единиц, обладающих данным признаком, и
доли единиц, не обладающим этим
признаком.
37.
Если значения 1 и 0 встречаются одинаковочасто, то дисперсия достигает своего
pq
=
0
,
25
.
максимума
Правило
сложения
дисперсий
распространяется и на дисперсии доли
признака, то есть доли единиц с
определенным признаком в совокупности,
разбитой на группы.
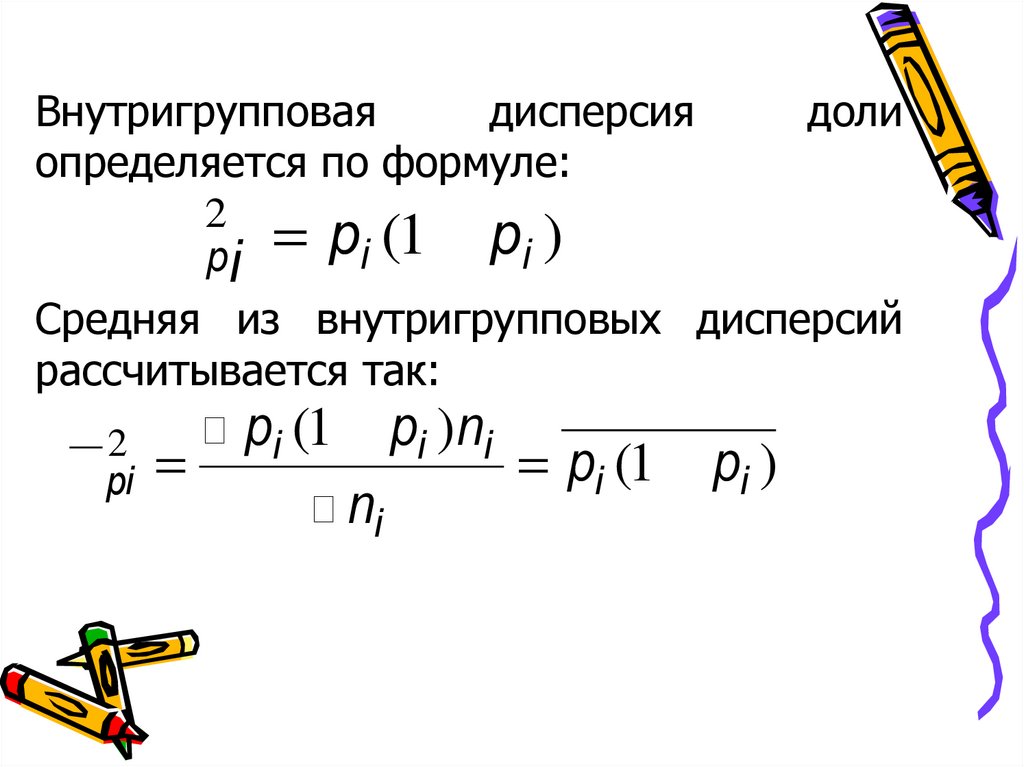
38.
Внутригрупповаядисперсия
определяется по формуле:
2
s pi = pi (1 - pi )
доли
Средняя из внутригрупповых дисперсий
рассчитывается так:
å pi (1 - pi ) ni
2
s pi =
= pi (1 - pi )
å ni
39.
Формула межгрупповой дисперсии имеетследующий вид:
å ( pi - p ) ni
2
d pi =
å ni
2
где ni – численность единиц в отдельных
группах;
рi – доля изучаемого признака во всей
совокупности, которая определяется по
формуле:
å pi ni
p=
å ni
40.
Общая дисперсия определяется по формуле:2
s p = p(1 - p).
Три вида дисперсий объединены между собой следующим
образом:
2
2
2
s p = s pi + d pi
Это – правило сложения дисперсии доли признака.
41.
Пример. Имеются следующие данные об удельномвесе основных рабочих в трех цехах фирмы:
Удельный вес основных рабочих фирмы
Цех
Удельный
вес Численность всех
основных рабочих в рабочих
% (pi)
1
80
100
2
75
200
3
90
150
Итого
450
42.
1) Определим долю основных рабочих вцелом по фирме (формула 30):
0,80 å100 + 0,75 å200 + 0,90 å150 365
p=
=
= 0,81
450
450
43.
2) Общая дисперсия доли основныхрабочих по всей фирме в целом будет
равна:
2
s p = 0,81 å(1 - 0,81) = 0,154
44.
3) Внутрицеховые дисперсии рассчитаем,применив формулу внутригрупповых
дисперсий:
2
s p1 = 0,8 å0,2 = 0,16;
2
s p 2 = 0,75 å0,25 = 0,19;
2
s p3 = 0,9 å0,1 = 0,09.
45.
4) Средняя из внутригрупповых дисперсийбудет равна:
2 0,16 å100 + 0,19 å200 + 0,09 å150 675
s pi =
= = 0,15
450
450
46.
Проверка вычислений показывает:0,154 = 0,15 + 0,004.
47.
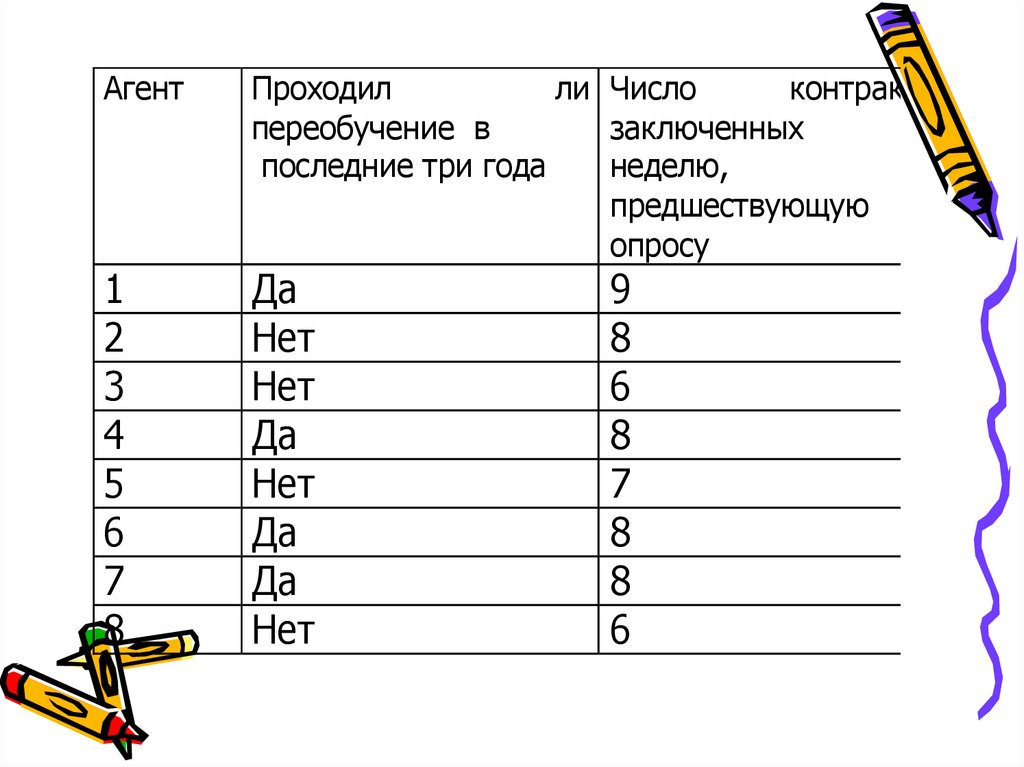
Пример. Большая торговая компания заказалаопрос, цель – выяснение влияния фактора
повышения квалификации на результаты работы
агентов по продажам. Опрос 8 торговых агентов
дал следующие результаты:
48.
АгентПроходил
ли Число
контрактов,
переобучение в
заключенных
за
последние три года
неделю,
предшествующую
опросу
1
2
3
4
5
6
7
8
Да
Нет
Нет
Да
Нет
Да
Да
Нет
9
8
6
8
7
8
8
6
49.
Среднеечисло
контрактов,
заключенных агентами:
k
å xi f i
9 + 8 å4 + 6 å2 + 7 9 + 32 + 12 + 7 60
i =1
x= r
=
=
= = 7,5
1+ 4 + 2 +1
8
8
å fi
i =1
В данном примере переподготовка –
факторный признак, а число заключаемых
контрактов – результативный.
50.
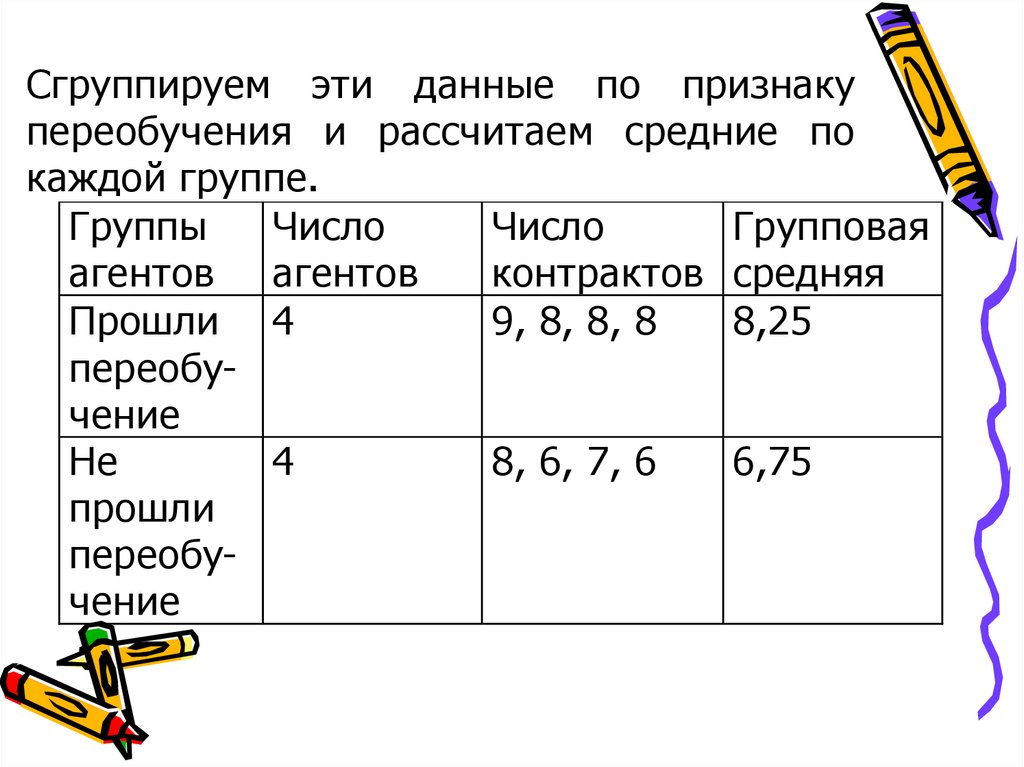
Сгруппируем эти данные по признакупереобучения и рассчитаем средние по
каждой группе.
Группы
Число
Число
Групповая
агентов агентов
контрактов средняя
Прошли 4
9, 8, 8, 8
8,25
переобучение
Не
4
8, 6, 7, 6
6,75
прошли
переобучение
51.
n1x1 =
å xi
i =1
n1
9+8+8+8
=
= 8,25
4
,
где n1 – число признаков в первой
группе.
Или
по
формуле
для
взвешенных
вариант
k1
x1 =
å xi
i =1
k1
å
i =1
fi
fi
9 + 3 å8
=
= 8,25
1+ 3
,
где fi – частоты ряда.
n2
å xi
8+7+6+6
x2 =
=
= 6,75
n2
4
,
i =1
где n2 – число признаков во второй группе.
52.
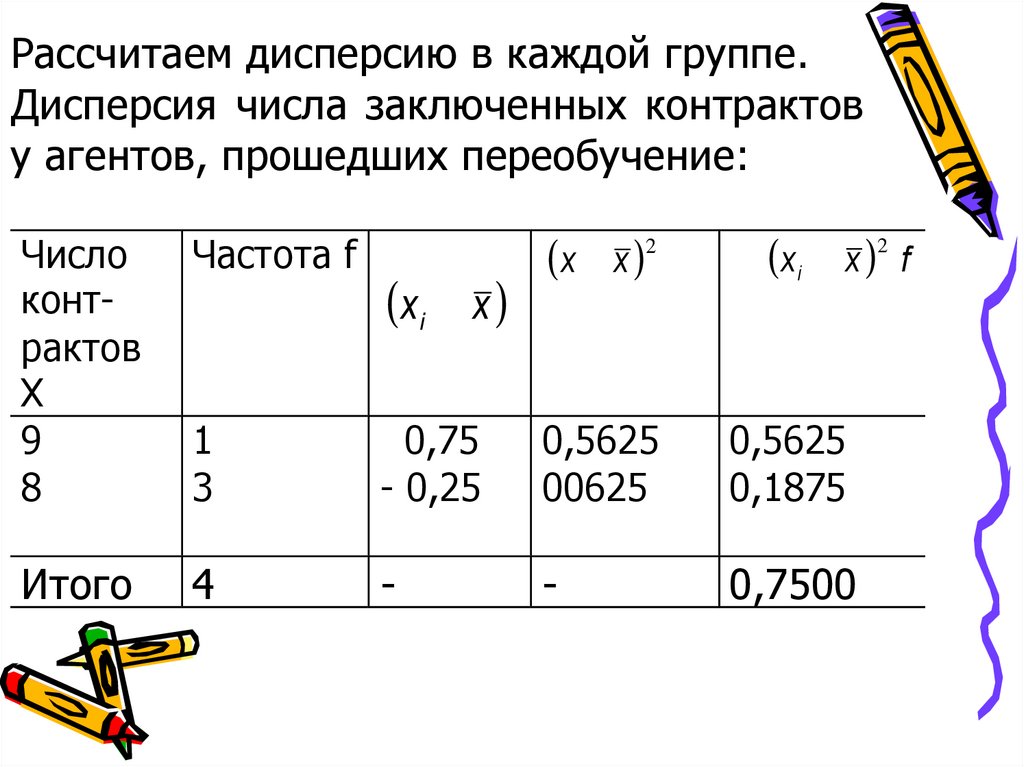
Рассчитаем дисперсию в каждой группе.Дисперсия числа заключенных контрактов
у агентов, прошедших переобучение:
( x - x )2
( x i - x )2 f
Число
контрактов
Х
9
8
Частота f
1
3
0,75
- 0,25
0,5625
00625
0,5625
0,1875
Итого
4
-
-
0,7500
( xi - x )
53.
(2 i =1
k1
s1 =
å xi - x
k1
å fi
i =1
) fi
2
0.75
=
= 0,1875
4
54.
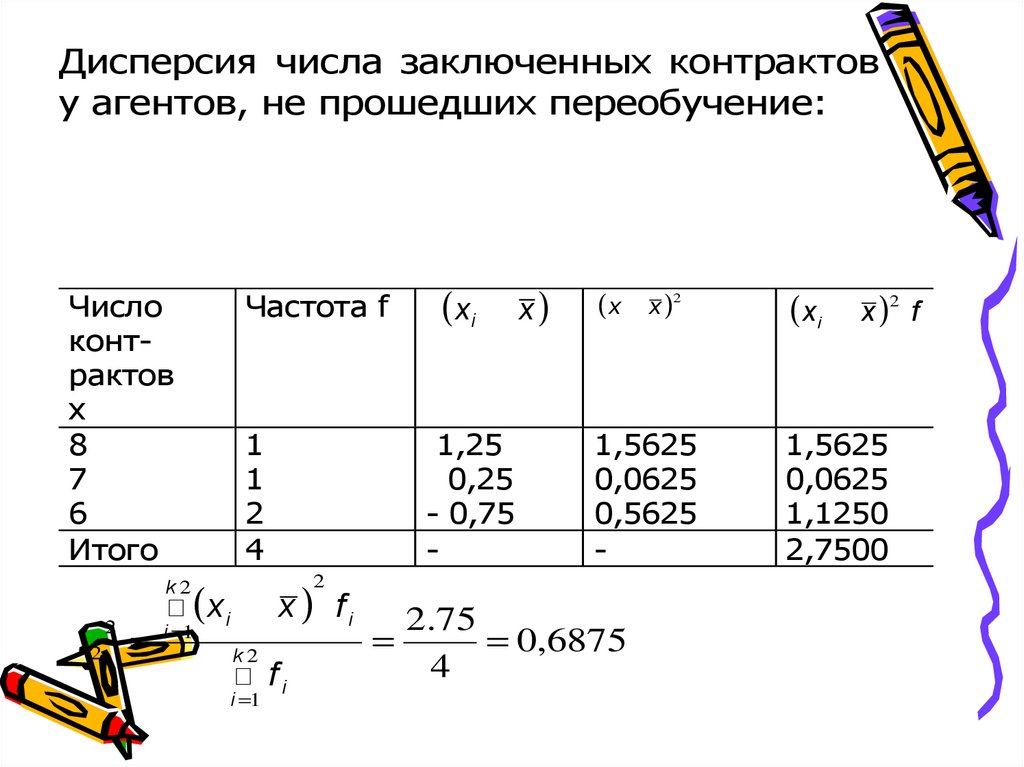
Дисперсия числа заключенных контрактову агентов, не прошедших переобучение:
Число
контрактов
Частота f
( xi - x )
(x - x )2
( x i - x )2 f
8
7
6
Итого
1
1
2
4
1,25
0,25
- 0,75
-
1,5625
0,0625
0,5625
-
1,5625
0,0625
1,1250
2,7500
x
(
xi - x ) f i
i =1
2
k2
s2 =
2
å
k2
å fi
i =1
2.75
=
= 0,6875
4
55.
Рассчитаем среднюю из внутригрупповыхдисперсий:
l
2
ås j nj
0,1875 å4 + 0,6875 å4
2
j =1
sj = l
=
= 0,4375
å nj
8
j =1
Этот показатель характеризует влияние на
результативный признак всех прочих
факторных признаков за исключением
признака,
положенного
в
основу
группировки.
56.
Очевидно, что различие в числезаключенных контрактов в двух группах
вызвано тем, что торговые агенты первой
группы прошли переобучение, а агенты
второй группы не прошли. Найдем
дисперсию между группами (межгрупповую
дисперсию). Согласно формуле :
l
d =
2
(
å xj - x
j =1
l
å nj
j =1
) n (8,25 - 7,5) å4 + (6,75 - 7,5) å4 2,25 + 2,25
=
=
= 0,5625
2
j
2
2
4+4
8
57.
Этот показатель характеризует влияниена результативный признак факторного
основу
в
положенного
признака,
группировки.
Общая дисперсия равна сумме средней из
межгрупповой
и
внутригрупповых
дисперсий:
2
2
2
j
s =d +s
правила
верность
Проверим
дисперсий. Рассчитаем общую
числа заключенных контрактов:
сложения
дисперсию
58.
Числоконтрактов х
Частота f
( xi - x ) ( x - x )2 ( x - x ) f
9
8
7
6
Итого
1
4
1
2
8
1,5
0,5
-0,5
-1,5
0
2
i
2,25
0,25
0,25
2,25
-
s2 = 8/8 = 1,00
В самом деле, 1,00 = 0,5625 + 0,4375.
2,25
1,00
0,25
4,50
8,00
59.
Поданным
примера
эмпирическое
корреляционное отношение равно:
d
h = 2 = 0,75
s
2
Следовательно, фактор, положенный в
основу группировки, существенно влияет
на
число
заключаемых
агентами
контрактов, но существуют и другие
факторы, влияние которых тоже заметно.















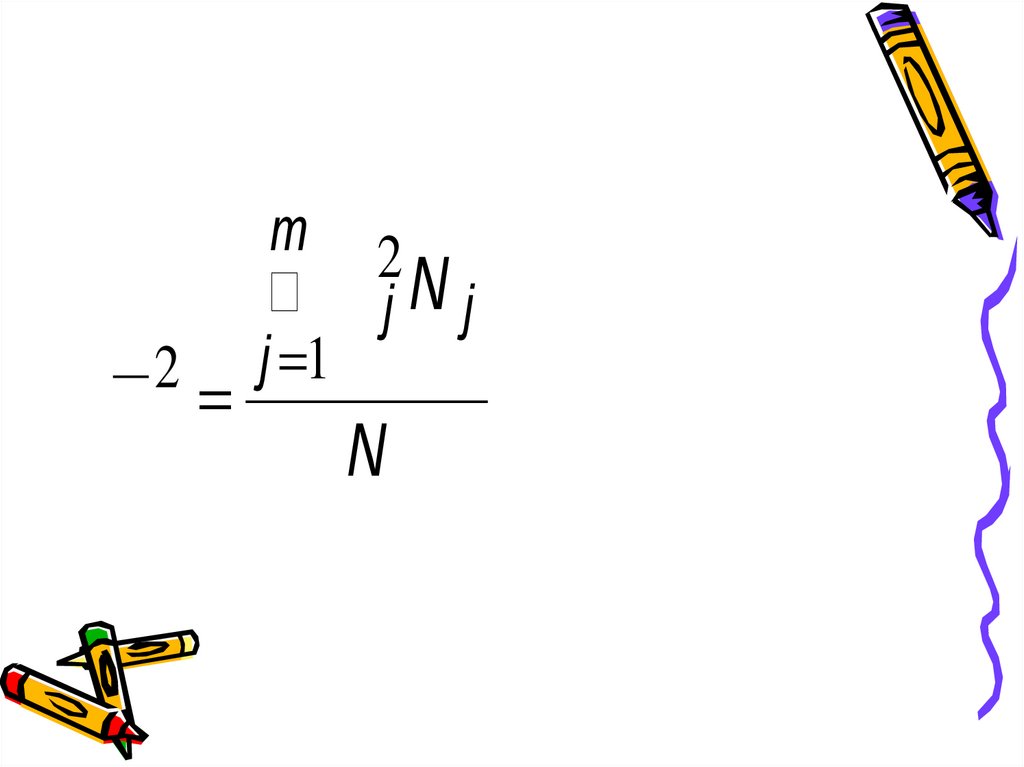




























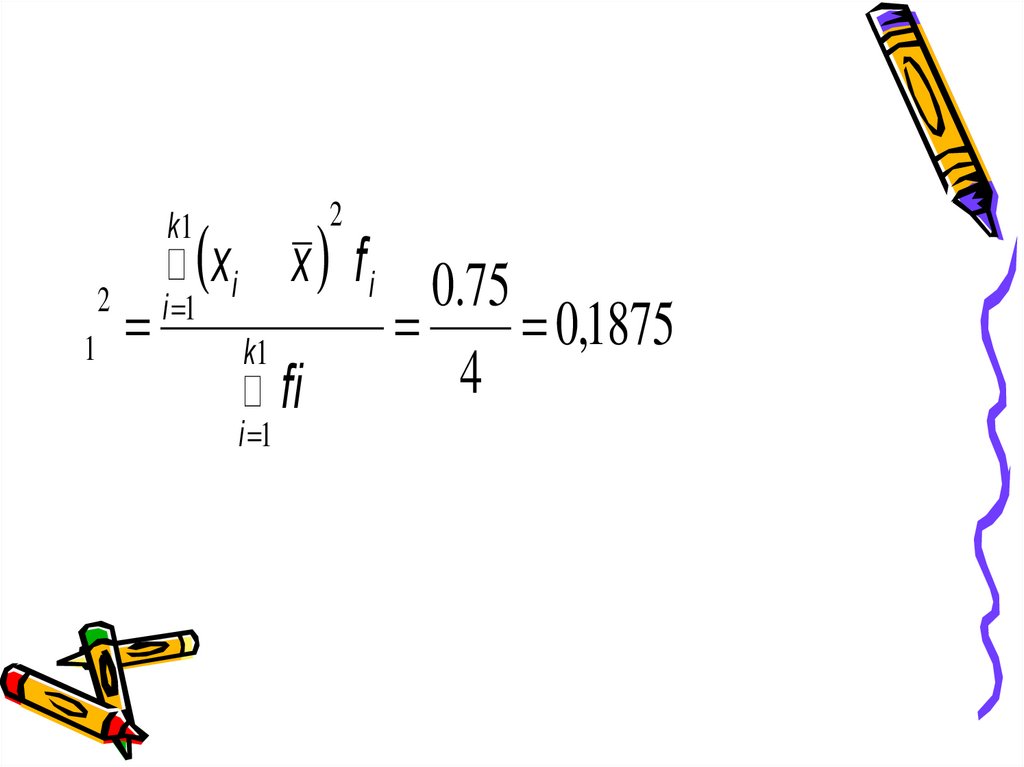





 mathematics
mathematics