Similar presentations:
Design and Analysis of Algorithms (DAA)
1.
Design and Analysisof Algorithms (DAA)
3621511 (6 cp)
Pasi Fränti
10.9.2018
2. DAA course at Autumn 2018
• Web: http://cs.uef.fi/pages/franti/asa/• ETCS 6
• Lectures (34h):
- Mon 14-17
- Tue 14-16
• Exercises (16h):
- Fri 10-12
• Exam dates: 2.11. 23.11.
2
3. Motivation
• Design- 90% cases simple algorithms found from
Bachelor level courses
- Focus on the 10% tough ones
• Analysis
– Why not just measure processing time?
– Time vs. space complexity analyses
– Upper and lower limits
3
4. Key concepts
• Problem- Can the problem be solved?
- How difficult is the problem?
- Real-life problems to algorithmic problems
• Algorithm
– How to find suitable algorithm?
– How to make it efficient?
• Instance
– Upper and lower limits
4
5.
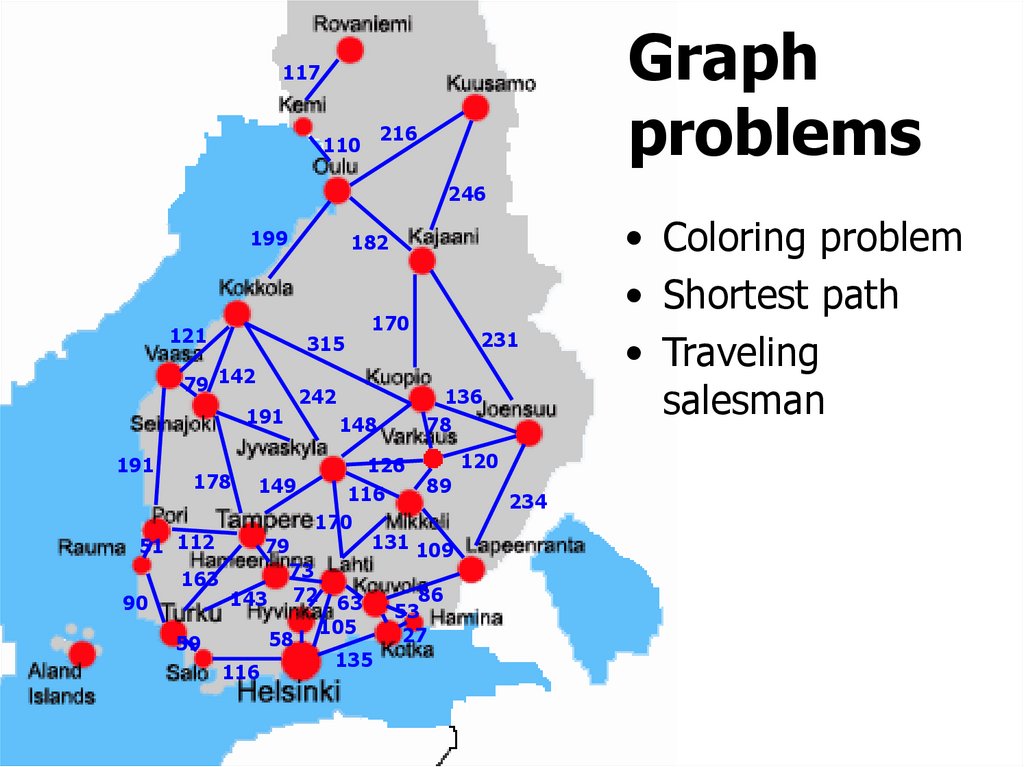
Graphproblems
117
216
110
246
199
121
182
315
79 142
191
170
242
148
231
136
78
120
126
149
89
116
234
170
131 109
51 112
79
73
163
86
143 72 63
90
53
105
27
58
59
135
116
191
178
• Coloring problem
• Shortest path
• Traveling
salesman
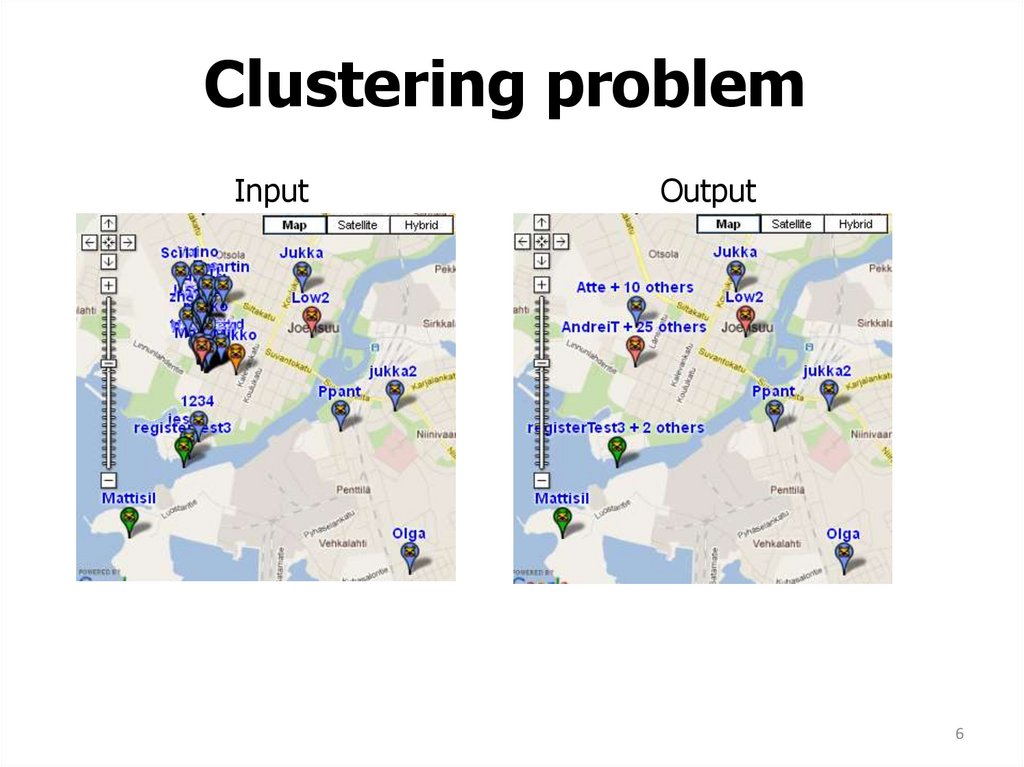
6. Clustering problem
InputOutput
6
7. What is algorithm?
• We need a well-specified problem that tellswhat needs to be achieved
• Algorithm solves the problem
• It consists of a sequence of commands that
takes an input and gives output
Input
Algorithm
Output
7
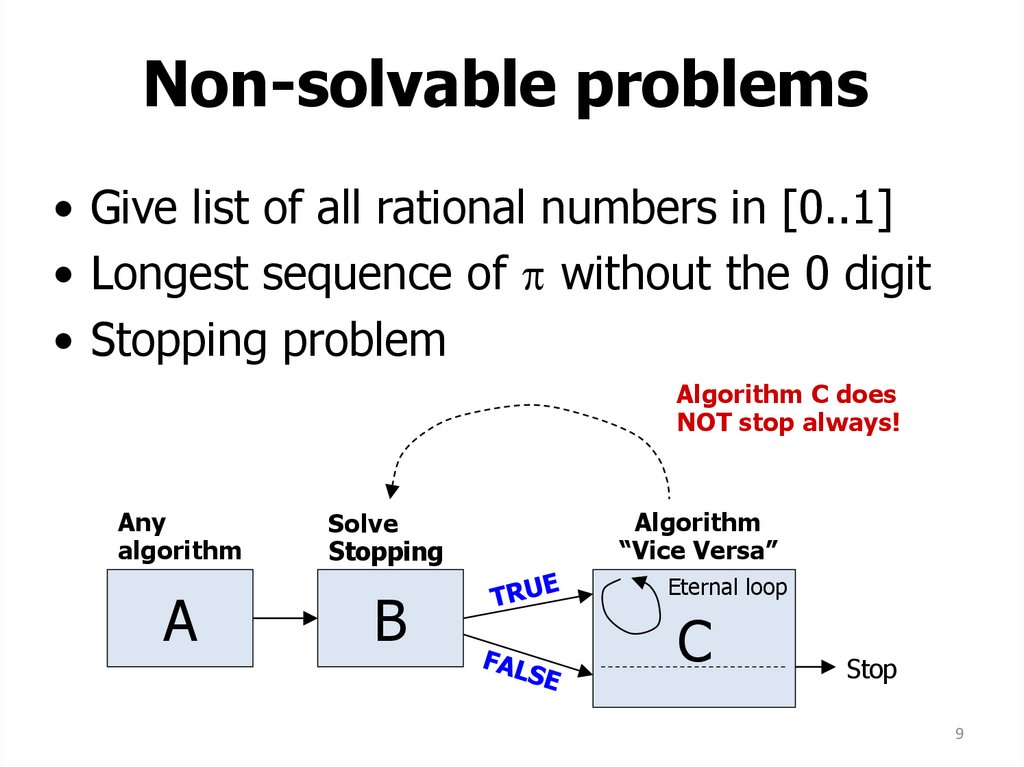
8. Non-solvable problems
• Give list of all rational numbers in [0..1]• Longest sequence of without the 0 digit
• Stopping problem
Does algorithm A
stop always?
Any
algorithm
Solve
Stopping
A
B
8
9. Non-solvable problems
• Give list of all rational numbers in [0..1]• Longest sequence of without the 0 digit
• Stopping problem
Algorithm C does
NOT stop always!
Any
algorithm
A
Solve
Stopping
B
Algorithm
“Vice Versa”
Eternal loop
C
Stop
9
10. Algorithm principles
• Sequence- One command at a time
- Parallel and distributed computing
• Condition
- IF
- CASE
• Loops
- FOR
- WHILE
- REPEAT
11. Complexity
Time complexity:– How much time it takes to compute
– Measured by a function T(N)
Space complexity:
– How much memory it takes to compute
– Measured by a function S(N)
11
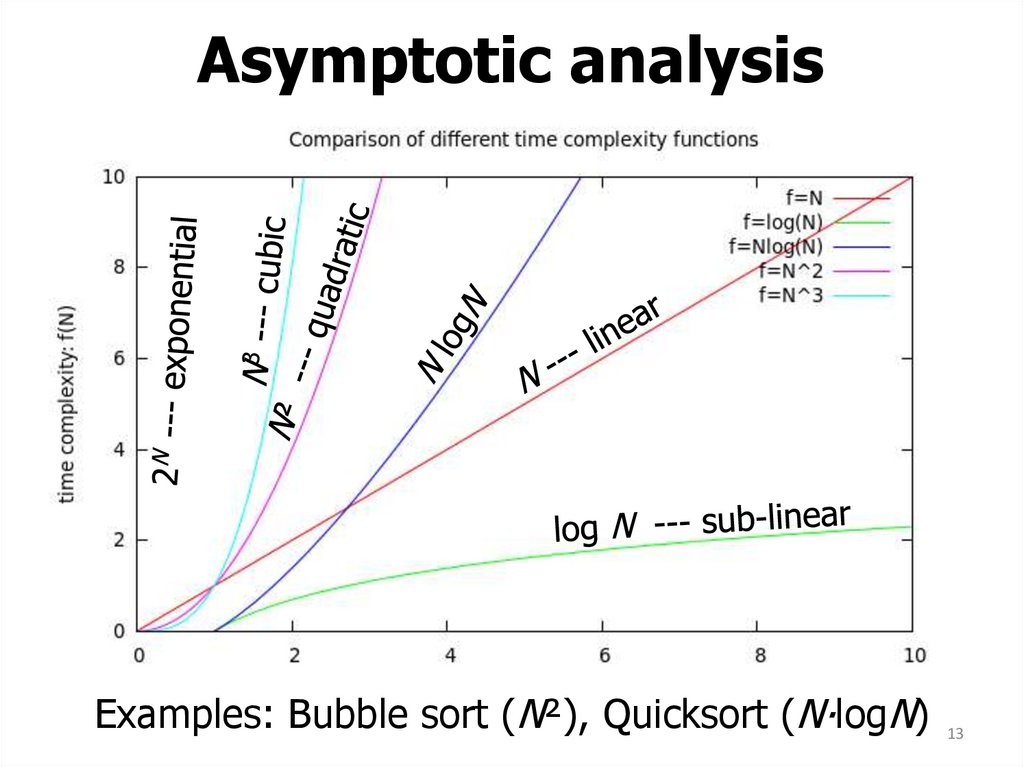
12. Time complexity
• N= Size of the input
• T(N) = Time complexity function
• Order of magnitude:
– How rapidly T(N) grows when N grows
– For example: O(N) O(logN) O(N²) O(2N)
12
13. Asymptotic analysis
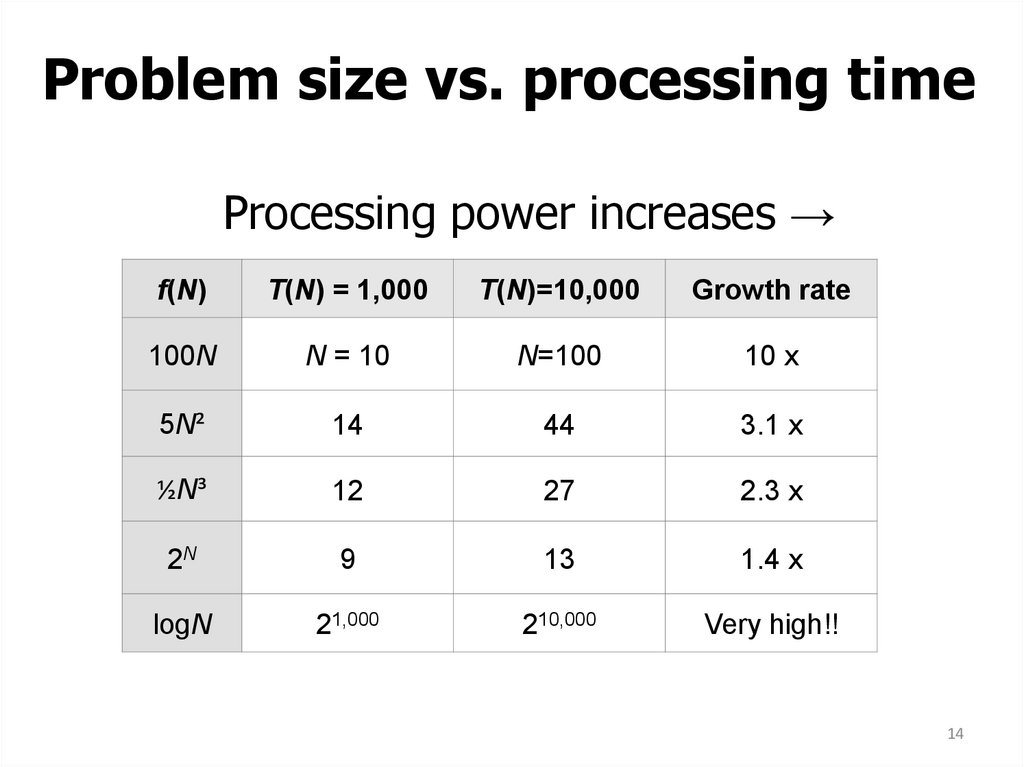
Examples: Bubble sort (N²), Quicksort (N∙logN) 1314. Problem size vs. processing time
Processing power increases →f(N)
T(N) = 1,000
T(N)=10,000
Growth rate
100N
N = 10
N=100
10 x
5N²
14
44
3.1 x
½N³
12
27
2.3 x
2N
9
13
1.4 x
logN
21,000
210,000
Very high!!
14
15. Exponential time complexity
12
4
8
16
256
512
1k
2k
…
32
64 128
1M
1G
Halfway…?
1T
1P
1E
Large than Everest
264 = 18.4 ∙ 1018
15












 informatics
informatics








