Floyd–Warshall algorithm

1. Floyd–Warshall algorithm

is an algorithm for finding shortest paths in a weighted graph with positive or negative edge
weights (but with no negative cycles/
Pseudocode for this basic version follows:
1 let dist be a |V| × |V| array of minimum distances initialized to ∞ (infinity)
2 for each edge (u,v)
3
dist[u][v] ← w(u,v) // the weight of the edge (u,v)
4 for each vertex v
5
dist[v][v] ← 0
6 for k from 1 to |V|
7
8
9
10
11
for i from 1 to |V|
for j from 1 to |V|
if dist[i][j] > dist[i][k] + dist[k][j]
dist[i][j] ← dist[i][k] + dist[k][j]
end if
1

2.

2

3.

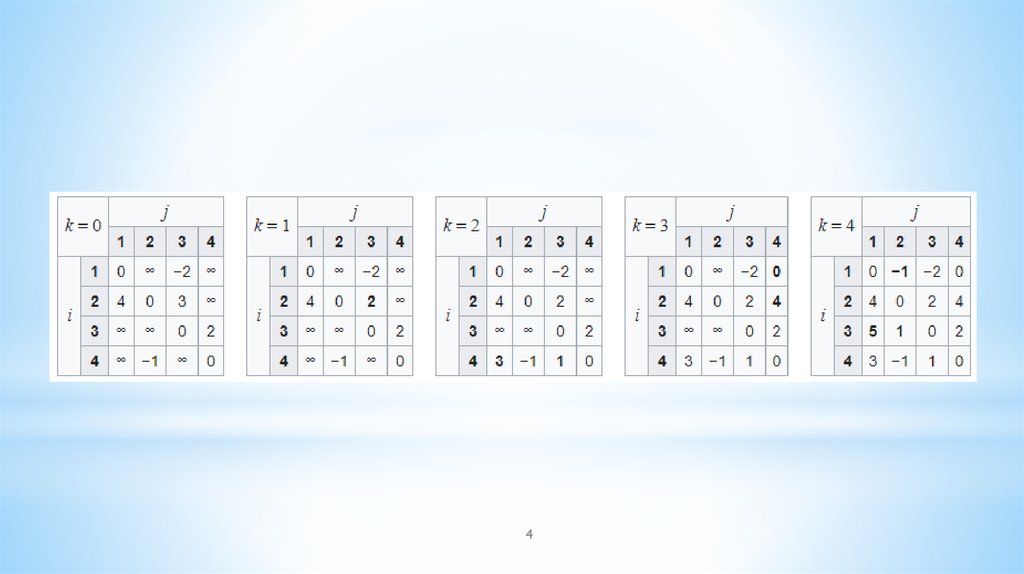
Prior to the first iteration of the outer loop, labeled k = 0 above, the
only known paths correspond to the single edges in the graph.
At k = 1, paths that go through the vertex 1 are found: in particular, the
path [2,1,3] is found, replacing the path [2,3] which has fewer edges
but is longer (in terms of weight).
At k = 2, paths going through the vertices {1,2} are found. The red and
blue boxes show how the path [4,2,1,3] is assembled from the two
known paths [4,2] and [2,1,3] encountered in previous iterations, with 2
in the intersection. The path [4,2,3] is not considered, because [2,1,3]
is the shortest path encountered so far from 2 to 3.
At k = 3, paths going through the vertices {1,2,3} are found.
Finally, at k = 4, all shortest paths are found.
3

4.

4

5.

5

6.

6

7.

7

8.

8

9.

9

10.

10

11.

11

12.

1. Prove that of six people, you can choose either three pairwise
acquaintances, or three pairwise unfamiliar ones.
2. In the graph in each vertex includes three edges. Prove that
there is at least one cycle in the graph.
3. On the plane, 100 circles are given, constituting a connected
(i.e., non-disintegrating) figure. Prove that this figure can be drawn
without taking the pencil from the paper and not drawing the same
line twice. Example of figure, that we can’t draw under this
condition:
12

13.

4. Visit all the cells of the chessboard 8х8 by the chess knight , having visited
each one once.
5. What is the greatest number of chess queens that can be placed on an
8x8 board, so that no two are on the same horizontal, vertical or
diagonal?
6. In the company of 2n + 1 people for any n people there is a different
person from them who is familiar with each of them. Prove that in this
company there is a person who knows everyone.
7. Among the participants of the conference, everyone has at least one
friend. Prove that the participants can be distributed in two rooms so
13
that each participant has a friend in the
other room.

14.

Sorting algorithms
14

15.

15

16.

Insertion sort is a simple sorting algorithm that is
relatively efficient for small lists and mostly sorted
lists, and is often used as part of more sophisticated
algorithms. It works by taking elements from the list
one by one and inserting them in their correct position
into a new sorted list. In arrays, the new list and the
remaining elements can share the array's space, but
insertion is expensive, requiring shifting all following
elements over by one.
Selection sort is an in-place comparison sort. The algorithm
finds the minimum value, swaps it with the value in the first
position, and repeats these steps for the remainder of the
list. Selection sort is noted for its simplicity, and also has
performance advantages over more complicated algorithms
in certain situations.

17.

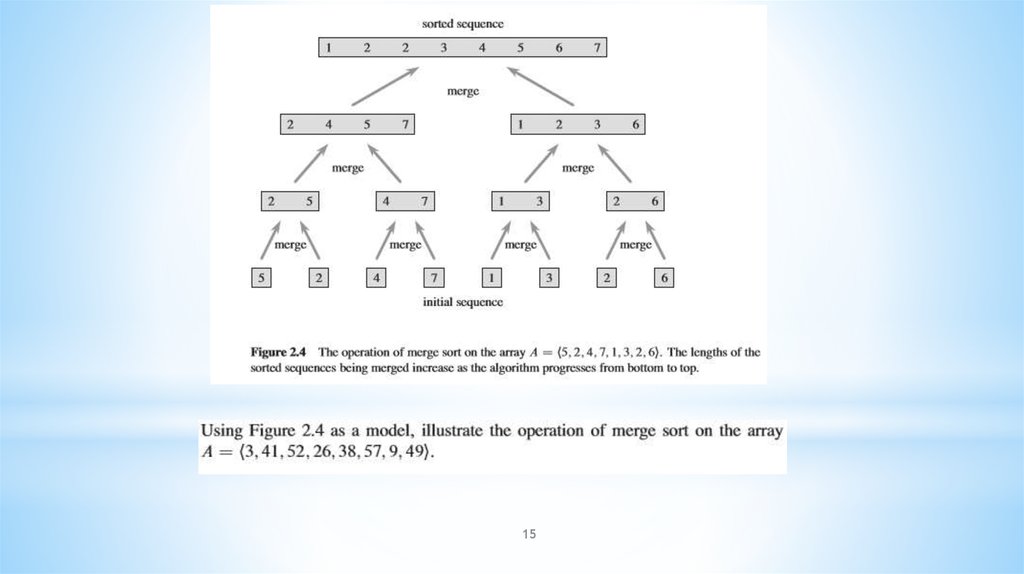
Merge sort takes advantage of the ease of merging
already sorted lists into a new sorted list. It starts by
comparing every two elements (i.e., 1 with 2, then 3
with 4...) and swapping them if the first should come
after the second. It then merges each of the resulting
lists of two into lists of four, then merges those lists of
four, and so on; until at last two lists are merged into
the final sorted list.

18.

Bucket sort is a divide and conquer sorting algorithm
that generalizes counting sort by partitioning an array
into a finite number of buckets. Each bucket is then
sorted individually, either using a different sorting
algorithm, or by recursively applying the bucket
sorting algorithm.
A bucket sort works best when the elements of the
data set are evenly distributed across all buckets.
Radix sort is an algorithm that sorts numbers by processing
individual digits. n numbers consisting of k digits each are
sorted in O(n · k) time. Radix sort can process digits of each
number either starting from the least significant digit or
starting from the most significant digit. The algorithm first
sorts the list by the least significant digit while preserving
their relative order using a stable sort. Then it sorts them
by the next digit, and so on from the least significant to the
most significant, ending up with a sorted list.