Similar presentations:
Greedy algorithms: introduction
1. Greedy Algorithms: Introduction
http://iti.wtfAlgorithms and Data Structures
Greedy Algorithms:
Introduction
Artem A. Golubnichiy
artem@golubnichij.ru
Department of Software of Computer Facilities and Automated Systems
Katanov Khakass State University
2. STRUCTURE OF THE CLASS
• Maximize Your Salary• Queue of Patients
• Implementation and Analysis
• Main Ingredients
2
3. WHAT’S COMING
• Solve salary maximization problem• Come up with a greedy algorithm yourself
• Solve optimal queue arrangement problem
• Generalize solutions using the concepts of greedy choice,
subproblem and safe choice
3
4. MAXIMIZE SALARY
45. MAXIMIZE SALARY
56. MAXIMIZE SALARY
67. LARGEST NUMBER
Toy problemWhat is the largest number that consists of digits 9, 8, 9, 6, 1? Use
all the digits.
7
8. LARGEST NUMBER
Toy problemWhat is the largest number that consists of digits 9, 8, 9, 6, 1? Use
all the digits.
Examples
16899, 69891, 98961, . . .
8
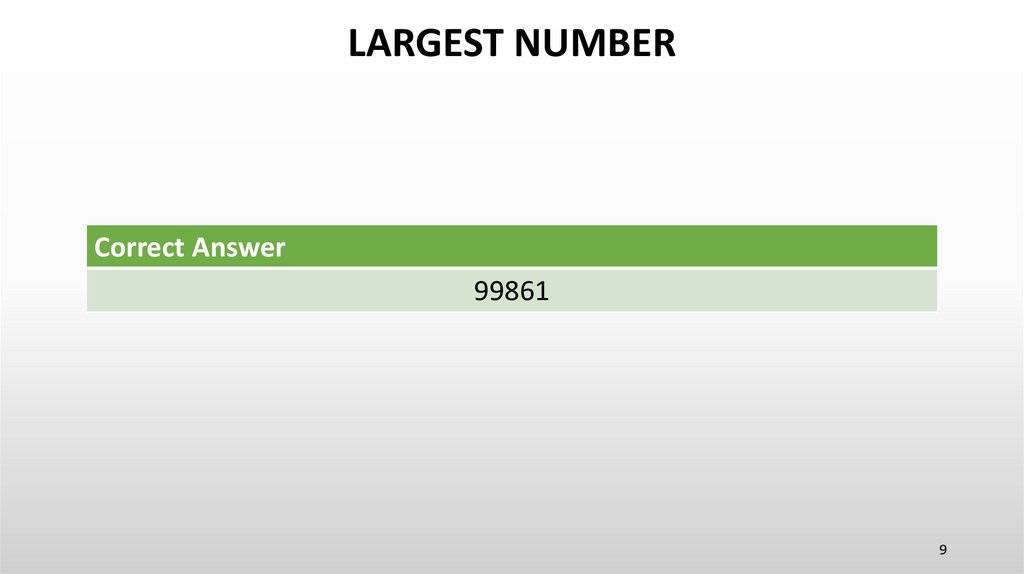
9. LARGEST NUMBER
Correct Answer99861
9
10. GREEDY STRATEGY
{9, 8, 9, 6, 1}→
? ? ? ? ?
10
11. GREEDY STRATEGY
Find max{9, 8, 9, 6, 1}
Find max digit
11
12. GREEDY STRATEGY
Find max{9, 8, 9, 6, 1}
Find max digit
12
13. GREEDY STRATEGY
Find max{9, 8, 9, 6, 1}
Append
→
Find max digit
Append it to the number
13
14. GREEDY STRATEGY
Find max{9, 8, 9, 6, 1}
Append
→
9
Find max digit
Append it to the number
14
15. GREEDY STRATEGY
Find max{9, 8, 9, 6, 1}
Append
→
9
Remove
Find max digit
Append it to the number
Remove it from the list of digits
15
16. GREEDY STRATEGY
Find max{9, 8, 9, 6, 1}
Append
→
9
Remove
Find max digit
Append it to the number
Remove it from the list of digits
16
17. GREEDY STRATEGY
Find max{8, 9, 6, 1}
Append
→
9
Remove
Find max digit
Append it to the number
Remove it from the list of digits
Repeat while there are digits in the list
17
18. GREEDY STRATEGY
Find max{8, 9, 6, 1}
Append
→
9
Remove
Find max digit
Append it to the number
Remove it from the list of digits
Repeat while there are digits in the list
18
19. GREEDY STRATEGY
Find max{8, 9, 6, 1}
Append
→
99
Remove
Find max digit
Append it to the number
Remove it from the list of digits
Repeat while there are digits in the list
19
20. GREEDY STRATEGY
Find max{8, 9, 6, 1}
Append
→
99
Remove
Find max digit
Append it to the number
Remove it from the list of digits
Repeat while there are digits in the list
20
21. GREEDY STRATEGY
Find max{8, 6, 1}
Append
→
99
Remove
Find max digit
Append it to the number
Remove it from the list of digits
Repeat while there are digits in the list
21
22. GREEDY STRATEGY
Find max{8, 6, 1}
Append
→
99
Remove
Find max digit
Append it to the number
Remove it from the list of digits
Repeat while there are digits in the list
22
23. GREEDY STRATEGY
Find max{8, 6, 1}
Append
→
998
Remove
Find max digit
Append it to the number
Remove it from the list of digits
Repeat while there are digits in the list
23
24. GREEDY STRATEGY
Find max{8, 6, 1}
Append
→
998
Remove
Find max digit
Append it to the number
Remove it from the list of digits
Repeat while there are digits in the list
24
25. GREEDY STRATEGY
Find max{6, 1}
Append
→
998
Remove
Find max digit
Append it to the number
Remove it from the list of digits
Repeat while there are digits in the list
25
26. GREEDY STRATEGY
Find max{6, 1}
Append
→
998
Remove
Find max digit
Append it to the number
Remove it from the list of digits
Repeat while there are digits in the list
26
27. GREEDY STRATEGY
Find max{6, 1}
Append
→
9986
Remove
Find max digit
Append it to the number
Remove it from the list of digits
Repeat while there are digits in the list
27
28. GREEDY STRATEGY
Find max{6, 1}
Append
→
9986
Remove
Find max digit
Append it to the number
Remove it from the list of digits
Repeat while there are digits in the list
28
29. GREEDY STRATEGY
Find max{1}
→
Append
9986
Remove
Find max digit
Append it to the number
Remove it from the list of digits
Repeat while there are digits in the list
29
30. GREEDY STRATEGY
Find max{1}
→
Append
9986
Remove
Find max digit
Append it to the number
Remove it from the list of digits
Repeat while there are digits in the list
30
31. GREEDY STRATEGY
Find max{1}
→
Append
99861
Remove
Find max digit
Append it to the number
Remove it from the list of digits
Repeat while there are digits in the list
31
32. GREEDY STRATEGY
Find max{1}
→
Append
99861
Remove
Find max digit
Append it to the number
Remove it from the list of digits
Repeat while there are digits in the list
32
33. GREEDY STRATEGY
Find max{}
→
Append
99861
Remove
Find max digit
Append it to the number
Remove it from the list of digits
Repeat while there are digits in the list
33
34. GREEDY STRATEGY
Find max{9, 8, 9, 6, 1}
Append
→
Remove
99861
Success!
Find max digit
Append it to the number
Remove it from the list of digits
Repeat while there are digits in the list
34
35. QUEUE OF PATIENTS
3536. QUEUE OF PATIENTS
Queue ArrangementInput:
n patients have come to the doctor’s office at 9:00AM. They
can be treated in any order. For i-th patient, the time needed
for treatment is ti. You need to arrange the patients in such a
queue that the total waiting time is minimized.
Output: The minimum total waiting time.
36
37. QUEUE OF PATIENTS
Optimal Queue Arrangementt1 =15, t2 =20 and t3 =10. Arrangement (1, 2, 3):
• First patient doesn’t wait
37
38. QUEUE OF PATIENTS
Optimal Queue Arrangementt1 =15, t2 =20 and t3 =10. Arrangement (1, 2, 3):
• First patient doesn’t wait
• Second patient waits for 15 minutes
38
39. QUEUE OF PATIENTS
Optimal Queue Arrangementt1 =15, t2 =20 and t3 =10. Arrangement (1, 2, 3):
• First patient doesn’t wait
• Second patient waits for 15 minutes
• Third patient waits for 15 + 20 = 35 minutes
39
40. QUEUE OF PATIENTS
Optimal Queue Arrangementt1 =15, t2 =20 and t3 =10. Arrangement (1, 2, 3):
• First patient doesn’t wait
• Second patient waits for 15 minutes
• Third patient waits for 15 + 20 = 35 minutes
• Total waiting time 15 + 35 = 50 minutes
40
41. QUEUE OF PATIENTS
Optimal Queue Arrangementt1 =15, t2 =20 and t3 =10. Arrangement (3, 1, 2):
• First patient doesn’t wait
41
42. QUEUE OF PATIENTS
Optimal Queue Arrangementt1 =15, t2 =20 and t3 =10. Arrangement (3, 1, 2):
• First patient doesn’t wait
• Second patient waits for 10 minutes
42
43. QUEUE OF PATIENTS
Optimal Queue Arrangementt1 =15, t2 =20 and t3 =10. Arrangement (3, 1, 2):
• First patient doesn’t wait
• Second patient waits for 10 minutes
• Third patient waits for 10 + 15 = 25 minutes
43
44. QUEUE OF PATIENTS
Optimal Queue Arrangementt1 =15, t2 =20 and t3 =10. Arrangement (3, 1, 2):
• First patient doesn’t wait
• Second patient waits for 10 minutes
• Third patient waits for 10 + 15 = 25 minutes
• Total waiting time 10 + 25 = 35 minutes
44
45. GREEDY STRATEGY
• Make some greedy choice• Reduce to a smaller problem
• Iterate
45
46. GREEDY CHOICE
• First treat the patient with the maximum treatment time• First treat the patient with the minimum treatment time
• First treat the patient with average treatment time
46
47. GREEDY ALGORITHM
• First treat the patient with the minimum treatment time47
48. GREEDY ALGORITHM
• First treat the patient with the minimum treatment time• Remove this patient from the queue
48
49. GREEDY ALGORITHM
• First treat the patient with the minimum treatment time• Remove this patient from the queue
• Treat all the remaining patients in such order as to minimize their total
waiting time
49
50. SUBPROBLEM
DefinitionSubproblem is a similar problem of smaller size.
50
51. SUBPROBLEM
Examples• MaximumSalary(1, 9, 8, 9, 6) =
51
52. SUBPROBLEM
Examples• MaximumSalary(1, 9, 8, 9, 6) =
‘‘9’’ + MaximumSalary(1, 8, 9, 6)
52
53. SUBPROBLEM
Examples• MaximumSalary(1, 9, 8, 9, 6) =
‘‘9’’ + MaximumSalary(1, 8, 9, 6)
• Minimum total waiting time for n patients = (n − 1) · tmin+
53
54. SUBPROBLEM
Examples• MaximumSalary(1, 9, 8, 9, 6) =
‘‘9’’ + MaximumSalary(1, 8, 9, 6)
• Minimum total waiting time for n patients = (n − 1) · tmin+ minimum
total waiting time for n − 1 patients without tmin
54
55. SAFE CHOICE
DefinitionA greedy choice is called safe choice if there is an optimal solution
consistent with this first choice.
55
56. SAFE CHOICE
LemmaTo treat the patient with minimum treatment time tmin first is a safe
choice.
56
57. PROOF IDEA
• Is it possible for an optimal arrangement to have two consecutive patients inorder with treatment times t1 and t2 such that t1 > t2?
57
58. PROOF IDEA
• Is it possible for an optimal arrangement to have two consecutive patients inorder with treatment times t1 and t2 such that t1 > t2?
• It is impossible. Assume there is such an optimal arrangement and consider
what happens if we swap these two patients.
58
59. PROOF IDEA
• Is it possible for an optimal arrangement to have two consecutive patients inorder with treatment times t1 and t2 such that t1 > t2?
• It is impossible. Assume there is such an optimal arrangement and consider
what happens if we swap these two patients.
• If we swap two consecutive patients with treatment times t1 > t2: Waiting
time for all the patients before and after these two doesn’t change
59
60. PROOF IDEA
• Is it possible for an optimal arrangement to have two consecutive patients inorder with treatment times t1 and t2 such that t1 > t2?
• It is impossible. Assume there is such an optimal arrangement and consider
what happens if we swap these two patients.
• If we swap two consecutive patients with treatment times t1 > t2: Waiting
time for all the patients before and after these two doesn’t change
• Waiting time for the patient which was first increases by t2, and for the
second one it decreases by t1
60
61. PROOF IDEA
• Is it possible for an optimal arrangement to have two consecutive patients inorder with treatment times t1 and t2 such that t1 > t2?
• It is impossible. Assume there is such an optimal arrangement and consider
what happens if we swap these two patients.
• If we swap two consecutive patients with treatment times t1 > t2: Waiting
time for all the patients before and after these two doesn’t change
• Waiting time for the patient which was first increases by t2, and for the
second one it decreases by t1
• Total waiting time increases by t2 − t1 < 0, so it actually decreases
61
62. PROOF IDEA
We have just proved:Lemma
In any optimal arrangement of the patients, first of any two consecutive
patients has smaller treatment time.
62
63. SAFE CHOICE PROOF
• Assume the patient with treatment time tmin is not the first63
64. SAFE CHOICE PROOF
• Assume the patient with treatment time tmin is not the first• Let i > 1 be the position of the first patient with treatment time tmin in the
optimal arrangement
64
65. SAFE CHOICE PROOF
• Assume the patient with treatment time tmin is not the first• Let i > 1 be the position of the first patient with treatment time tmin in the
optimal arrangement
• Then the patient at position i − 1 has bigger treatment time — a
contradiction
65
66. Conclusion
Now we know that the following greedy algorithm works correctly:• First treat the patient with the minimum treatment time
66
67. Conclusion
Now we know that the following greedy algorithm works correctly:• First treat the patient with the minimum treatment time
• Remove this patient from the queue
67
68. Conclusion
Now we know that the following greedy algorithm works correctly:• First treat the patient with the minimum treatment time
• Remove this patient from the queue
• Treat all the remaining patients in such order as to minimize their total
waiting time
68
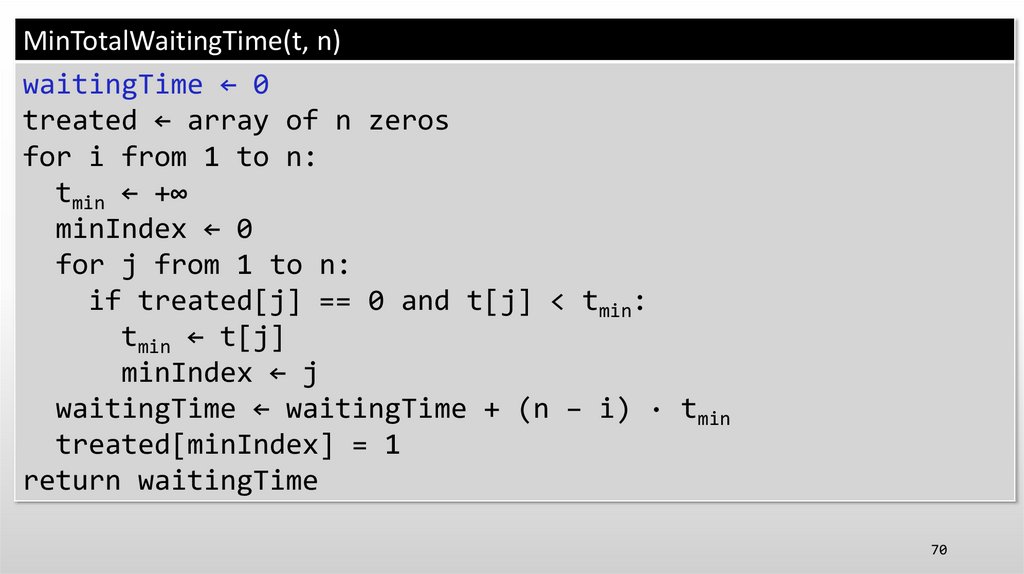
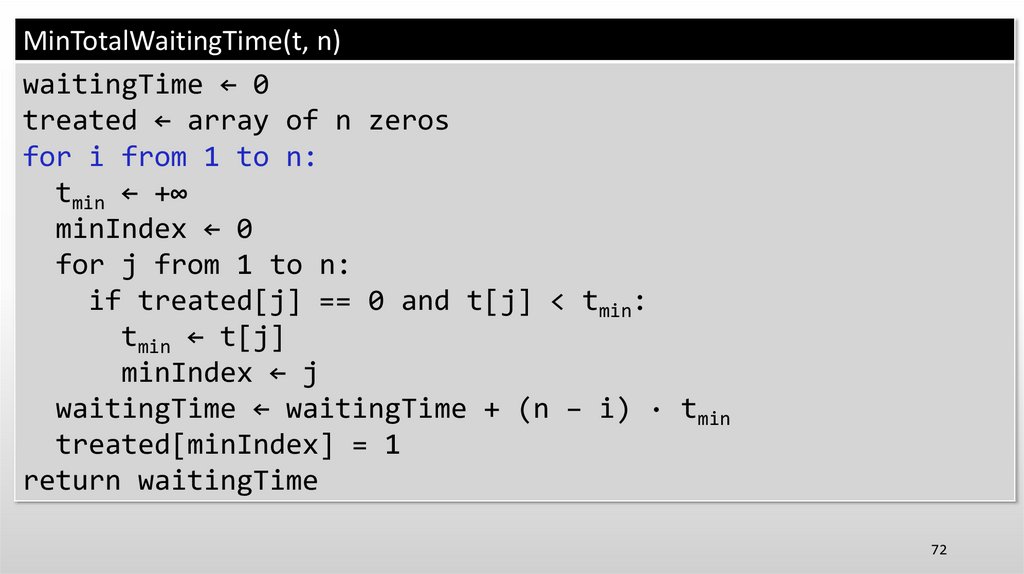
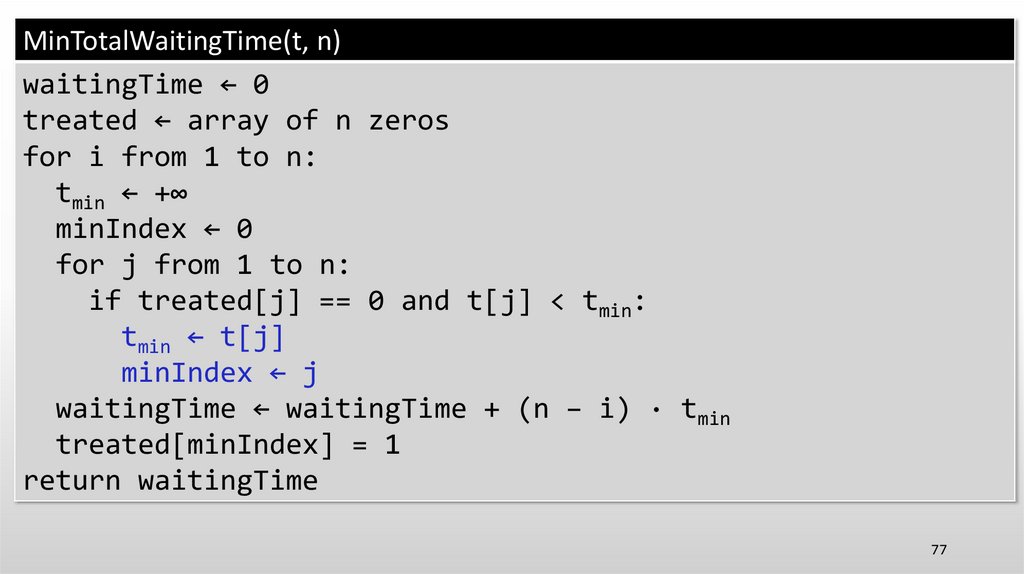
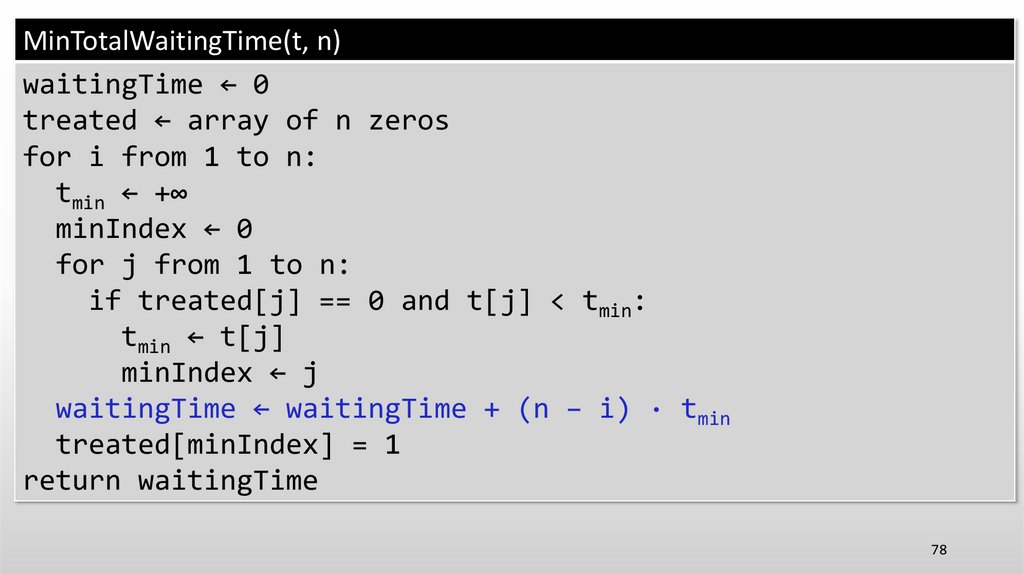
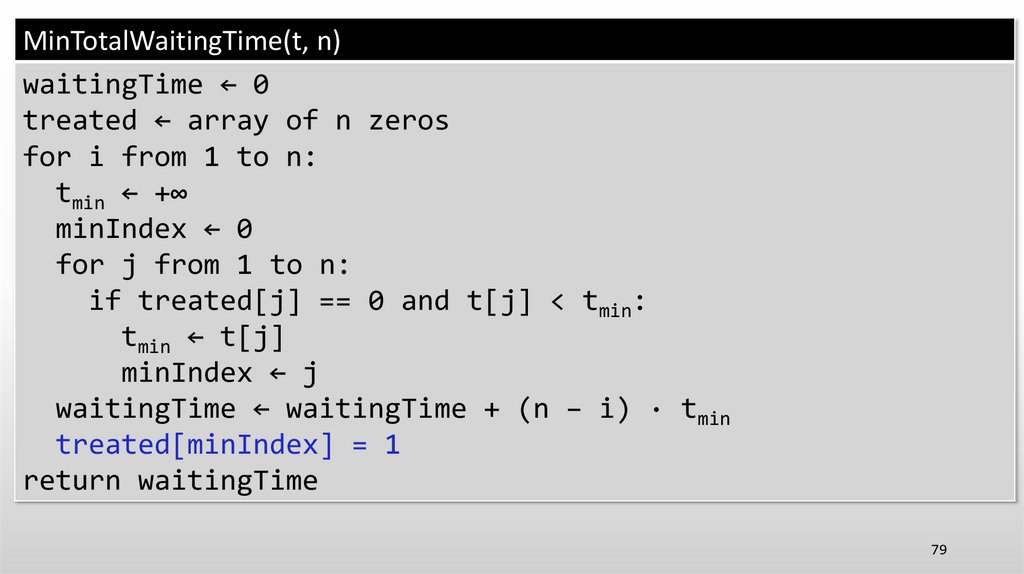
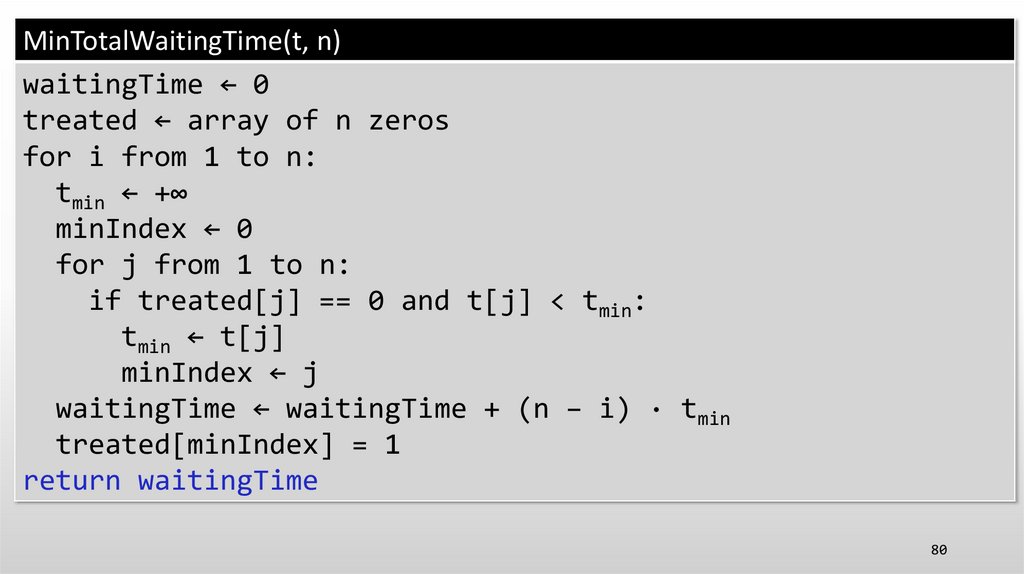
69.
MinTotalWaitingTime(t, n)waitingTime ← 0
treated ← array of n zeros
for i from 1 to n:
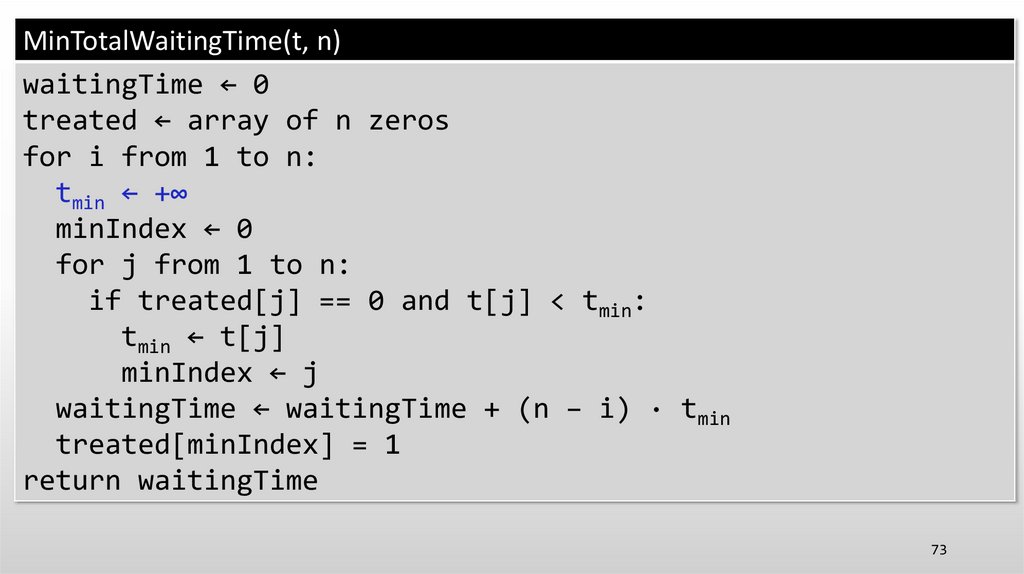
tmin ← +∞
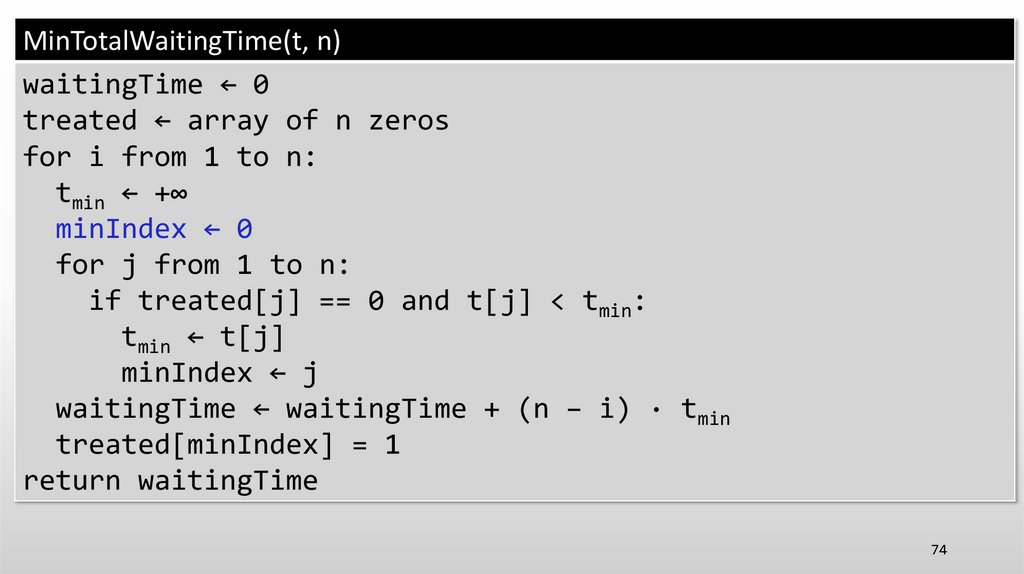
minIndex ← 0
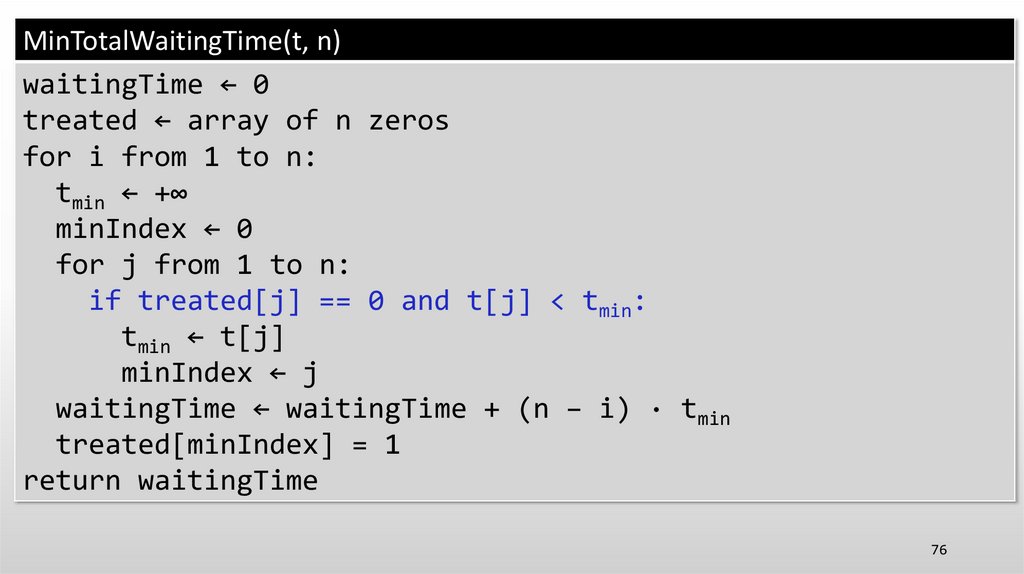
for j from 1 to n:
if treated[j] == 0 and t[j] < tmin:
tmin ← t[j]
minIndex ← j
waitingTime ← waitingTime + (n − i) · tmin
treated[minIndex] = 1
return waitingTime
69
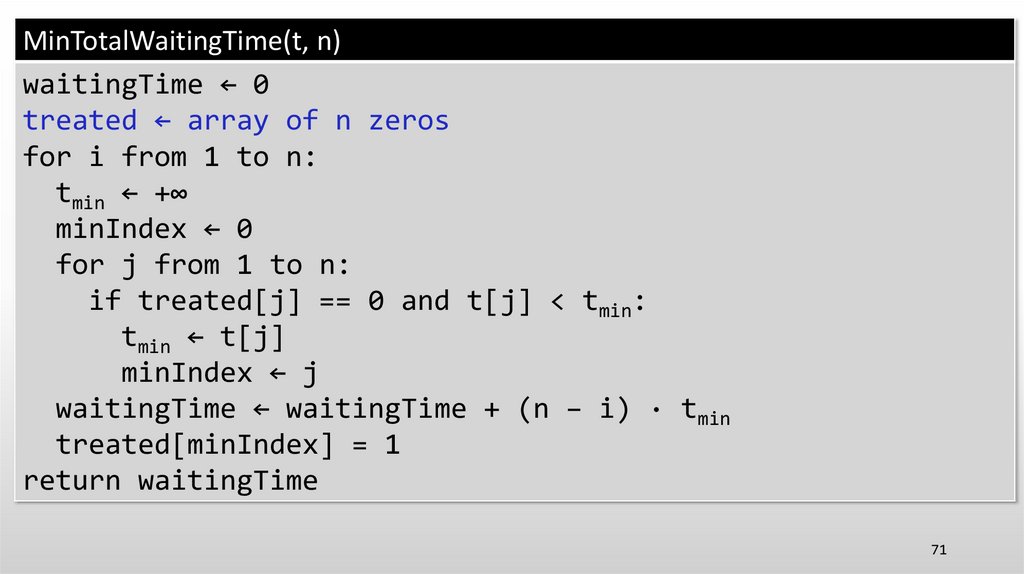
70.
MinTotalWaitingTime(t, n)waitingTime ← 0
treated ← array of n zeros
for i from 1 to n:
tmin ← +∞
minIndex ← 0
for j from 1 to n:
if treated[j] == 0 and t[j] < tmin:
tmin ← t[j]
minIndex ← j
waitingTime ← waitingTime + (n − i) · tmin
treated[minIndex] = 1
return waitingTime
70
71.
MinTotalWaitingTime(t, n)waitingTime ← 0
treated ← array of n zeros
for i from 1 to n:
tmin ← +∞
minIndex ← 0
for j from 1 to n:
if treated[j] == 0 and t[j] < tmin:
tmin ← t[j]
minIndex ← j
waitingTime ← waitingTime + (n − i) · tmin
treated[minIndex] = 1
return waitingTime
71
72.
MinTotalWaitingTime(t, n)waitingTime ← 0
treated ← array of n zeros
for i from 1 to n:
tmin ← +∞
minIndex ← 0
for j from 1 to n:
if treated[j] == 0 and t[j] < tmin:
tmin ← t[j]
minIndex ← j
waitingTime ← waitingTime + (n − i) · tmin
treated[minIndex] = 1
return waitingTime
72
73.
MinTotalWaitingTime(t, n)waitingTime ← 0
treated ← array of n zeros
for i from 1 to n:
tmin ← +∞
minIndex ← 0
for j from 1 to n:
if treated[j] == 0 and t[j] < tmin:
tmin ← t[j]
minIndex ← j
waitingTime ← waitingTime + (n − i) · tmin
treated[minIndex] = 1
return waitingTime
73
74.
MinTotalWaitingTime(t, n)waitingTime ← 0
treated ← array of n zeros
for i from 1 to n:
tmin ← +∞
minIndex ← 0
for j from 1 to n:
if treated[j] == 0 and t[j] < tmin:
tmin ← t[j]
minIndex ← j
waitingTime ← waitingTime + (n − i) · tmin
treated[minIndex] = 1
return waitingTime
74
75.
MinTotalWaitingTime(t, n)waitingTime ← 0
treated ← array of n zeros
for i from 1 to n:
tmin ← +∞
minIndex ← 0
for j from 1 to n:
if treated[j] == 0 and t[j] < tmin:
tmin ← t[j]
minIndex ← j
waitingTime ← waitingTime + (n − i) · tmin
treated[minIndex] = 1
return waitingTime
75
76.
MinTotalWaitingTime(t, n)waitingTime ← 0
treated ← array of n zeros
for i from 1 to n:
tmin ← +∞
minIndex ← 0
for j from 1 to n:
if treated[j] == 0 and t[j] < tmin:
tmin ← t[j]
minIndex ← j
waitingTime ← waitingTime + (n − i) · tmin
treated[minIndex] = 1
return waitingTime
76
77.
MinTotalWaitingTime(t, n)waitingTime ← 0
treated ← array of n zeros
for i from 1 to n:
tmin ← +∞
minIndex ← 0
for j from 1 to n:
if treated[j] == 0 and t[j] < tmin:
tmin ← t[j]
minIndex ← j
waitingTime ← waitingTime + (n − i) · tmin
treated[minIndex] = 1
return waitingTime
77
78.
MinTotalWaitingTime(t, n)waitingTime ← 0
treated ← array of n zeros
for i from 1 to n:
tmin ← +∞
minIndex ← 0
for j from 1 to n:
if treated[j] == 0 and t[j] < tmin:
tmin ← t[j]
minIndex ← j
waitingTime ← waitingTime + (n − i) · tmin
treated[minIndex] = 1
return waitingTime
78
79.
MinTotalWaitingTime(t, n)waitingTime ← 0
treated ← array of n zeros
for i from 1 to n:
tmin ← +∞
minIndex ← 0
for j from 1 to n:
if treated[j] == 0 and t[j] < tmin:
tmin ← t[j]
minIndex ← j
waitingTime ← waitingTime + (n − i) · tmin
treated[minIndex] = 1
return waitingTime
79
80.
MinTotalWaitingTime(t, n)waitingTime ← 0
treated ← array of n zeros
for i from 1 to n:
tmin ← +∞
minIndex ← 0
for j from 1 to n:
if treated[j] == 0 and t[j] < tmin:
tmin ← t[j]
minIndex ← j
waitingTime ← waitingTime + (n − i) · tmin
treated[minIndex] = 1
return waitingTime
80
81.
LemmaThe running time of MinTotalWaitingTime(t, n) is O(n2).
81
82.
LemmaThe running time of MinTotalWaitingTime(t, n) is O(n2).
Proof
• i changes from 1 to n
82
83.
LemmaThe running time of MinTotalWaitingTime(t, n) is O(n2).
Proof
• i changes from 1 to n
• For each value of i, j changes from 1 to n
83
84.
LemmaThe running time of MinTotalWaitingTime(t, n) is O(n2).
Proof
• i changes from 1 to n
• For each value of i, j changes from 1 to n
• This results in O(n2)
84
85.
• Actually, this problem can be solved in time O(n log n)85
86.
• Actually, this problem can be solved in time O(n log n)• Instead of choosing the patient with minimum treatment time
out of remaining ones n times, sort patients by increasing
treatment time
86
87.
• Actually, this problem can be solved in time O(n log n)• Instead of choosing the patient with minimum treatment time
out of remaining ones n times, sort patients by increasing
treatment time
• This sorted arrangement is optimal
87
88.
• Actually, this problem can be solved in time O(n log n)• Instead of choosing the patient with minimum treatment time
out of remaining ones n times, sort patients by increasing
treatment time
• This sorted arrangement is optimal
• It is possible to sort n patients in time O(n log n)
88
89.
REDUCTION TO SUBPROBLEM• Make some first choice
• Then solve a problem of the same kind
• Smaller: fewer digits, fewer patients
• This is called a “subproblem”
89
90.
SAFE CHOICE• A choice is called safe if there is an optimal solution consistent with
this first choice
90
91.
SAFE CHOICE• A choice is called safe if there is an optimal solution consistent with
this first choice
• Not all first choices are safe
91
92.
SAFE CHOICE• A choice is called safe if there is an optimal solution consistent with
this first choice
• Not all first choices are safe
• Greedy choices are often unsafe
92
93.
GENERAL STRATEGYProblem
93
94.
GENERAL STRATEGYgreedy choice
Problem
Make a greedy choice
94
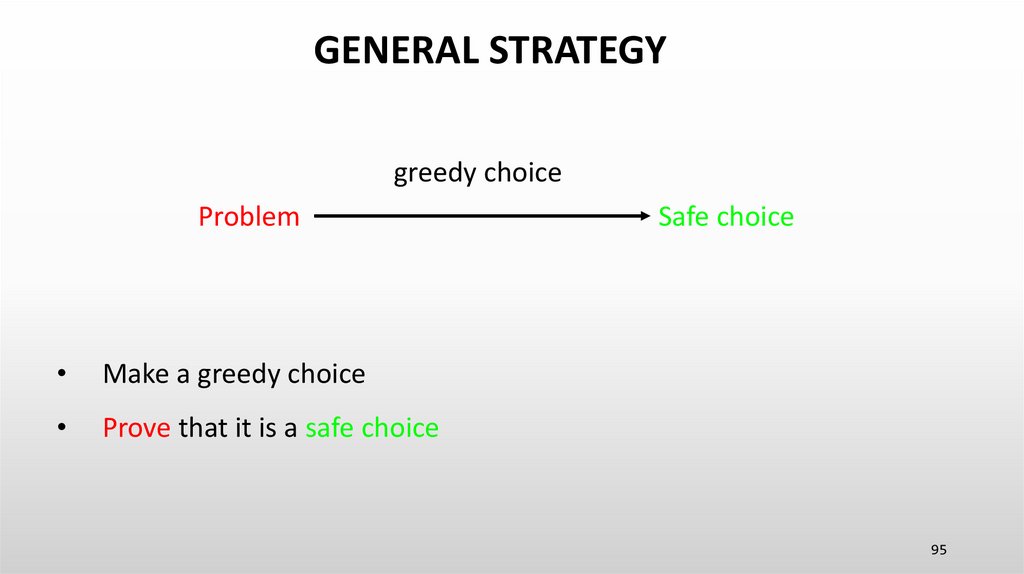
95.
GENERAL STRATEGYgreedy choice
Problem
Make a greedy choice
Prove that it is a safe choice
Safe choice
95
96.
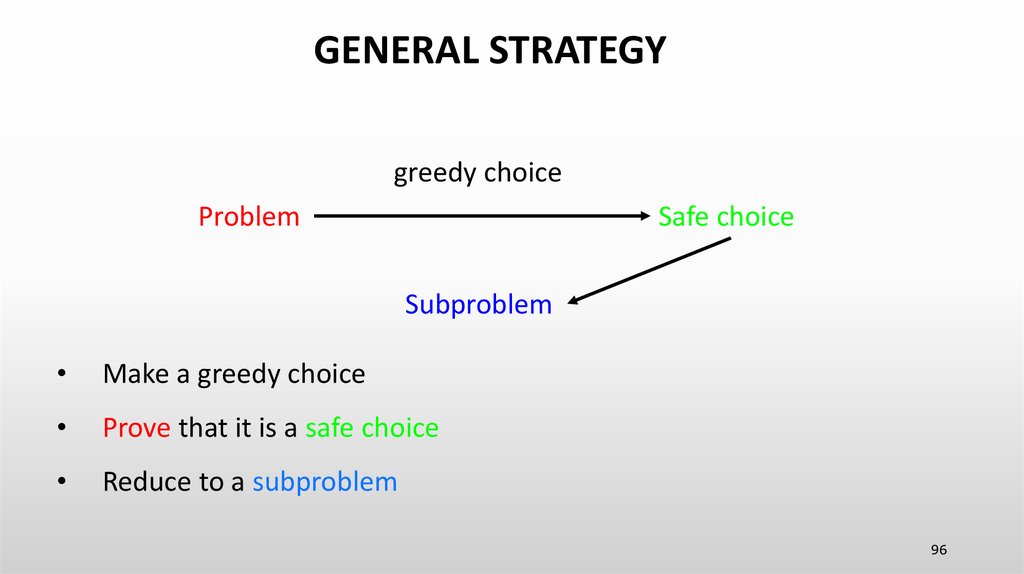
GENERAL STRATEGYgreedy choice
Problem
Safe choice
Subproblem
Make a greedy choice
Prove that it is a safe choice
Reduce to a subproblem
96
97.
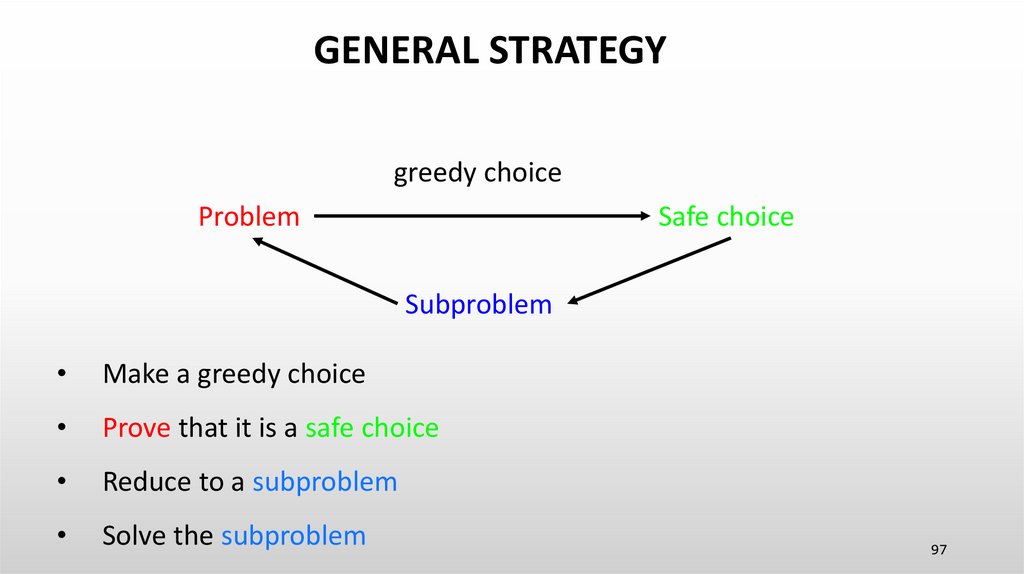
GENERAL STRATEGYgreedy choice
Problem
Safe choice
Subproblem
Make a greedy choice
Prove that it is a safe choice
Reduce to a subproblem
Solve the subproblem
97













































































 informatics
informatics








