Similar presentations:
Задачи по теме «Смежные и вертикальные углы». 7 класс
1.
7 класс, ГеометрияЗадачи
по теме
«Смежные и вертикальные
углы»
2.
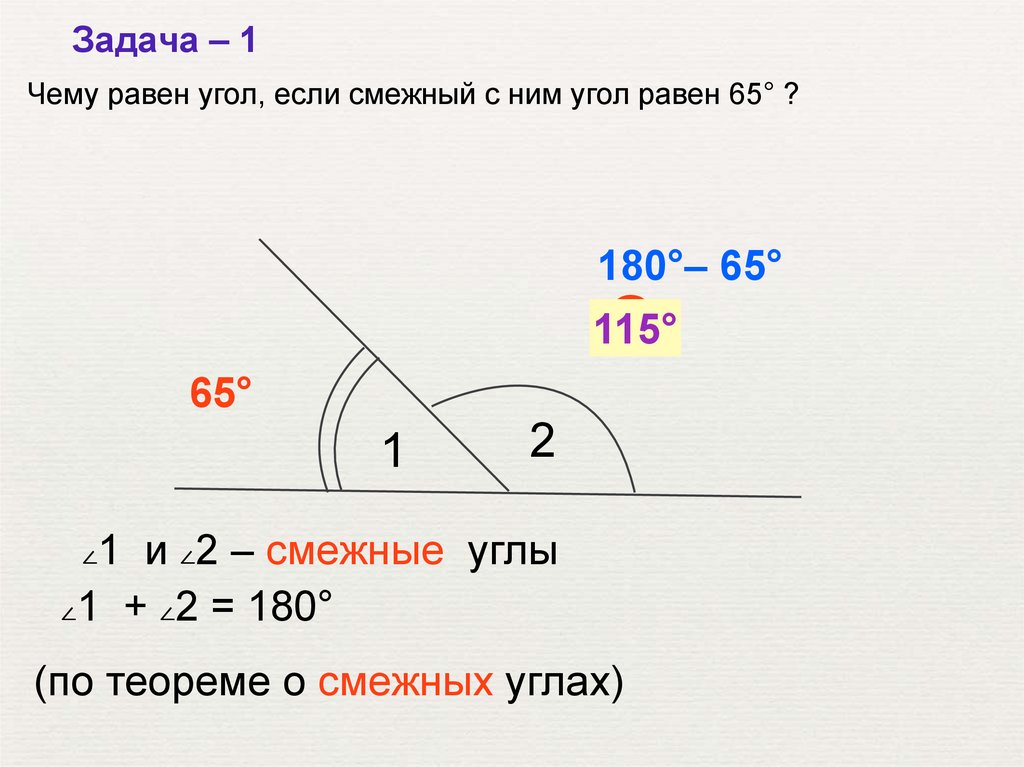
Задача – 1Чему равен угол, если смежный с ним угол равен 65° ?
180°– 65°
?
115°
65°
1
2
1 и ∠2 – смежные углы
∠1 + ∠2 = 180°
∠
(по теореме о смежных углах)
3.
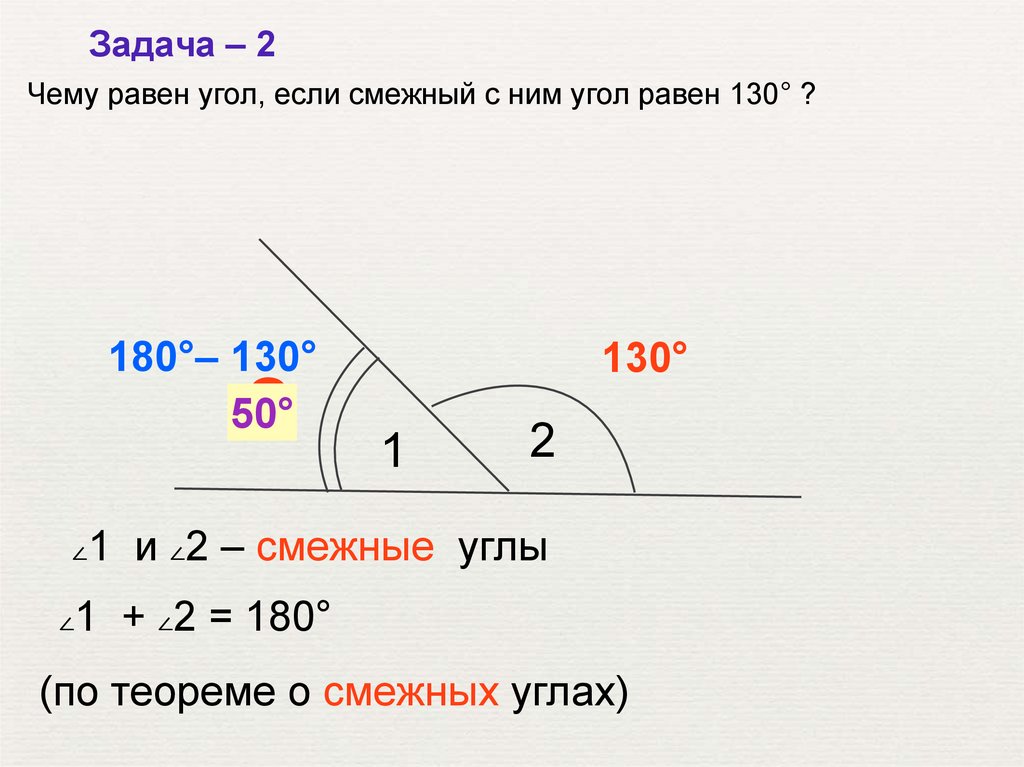
Задача – 2Чему равен угол, если смежный с ним угол равен 130° ?
180°– 130°
50°
?
∠
∠
130°
1
2
1 и ∠2 – смежные углы
1 + ∠2 = 180°
(по теореме о смежных углах)
4.
Задача – 3Чему равен угол 2 ?
∠
1 и ∠2 – вертикальные углы
1 = ∠2 (по теореме о
∠
вертикальных углах)
73°
1
2
73°
?
5.
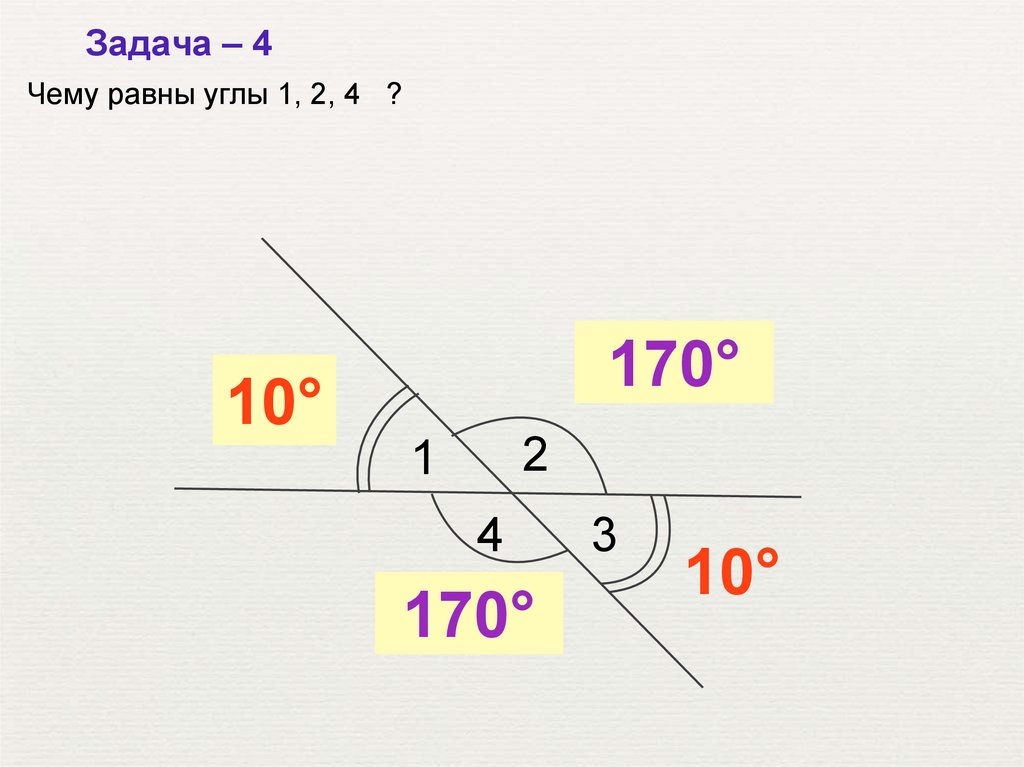
Задача – 4Чему равны углы 1, 2, 4 ?
10°
?
10°
?180°–
170°
2
1
4
170°
?
3
10°
6.
Один из смежных углов в 3 раза больше другого.Найдите эти углы.
Задача – 5
45°
x?
3x
135°
?
в 3 раза
больше
1
Дано: ∠1 и ∠2 – смежные
∠2 в 3 раза больше ∠1
Найти: ∠1 и ∠2
2
Решение.
Пусть ∠1 = х, тогда ∠2 = 3х
∠1 + ∠2 = 180° (по теореме о смежных углах)
х + 3х = 180°
∠2 = 180° – ∠1 = 180° – 45° = 135°
4х = 180°
х = 180° : 4
х = 45° – угол 1
Ответ: ∠1 = 45°, ∠2 = 135°
7.
Задача – 6Дано: ∠1 и ∠2 – смежные
144°
?
4х
х
в 4 раза
меньше
36°
?
Один из смежных углов в 4 раза меньше другого.
Найдите эти углы.
1
∠1 в 4 раза меньше ∠2
Найти: ∠1 и ∠2
2
Решение.
Пусть ∠1 = х, тогда ∠2 = 4х
∠1 + ∠2 = 180° (по теореме о смежных углах)
х + 4х = 180°
∠2 = 180° – ∠1 = 180° – 36° = 144°
5х = 180°
х = 180° : 5
х = 36° – угол 1
Ответ: ∠1 = 36°, ∠2 = 144°
8.
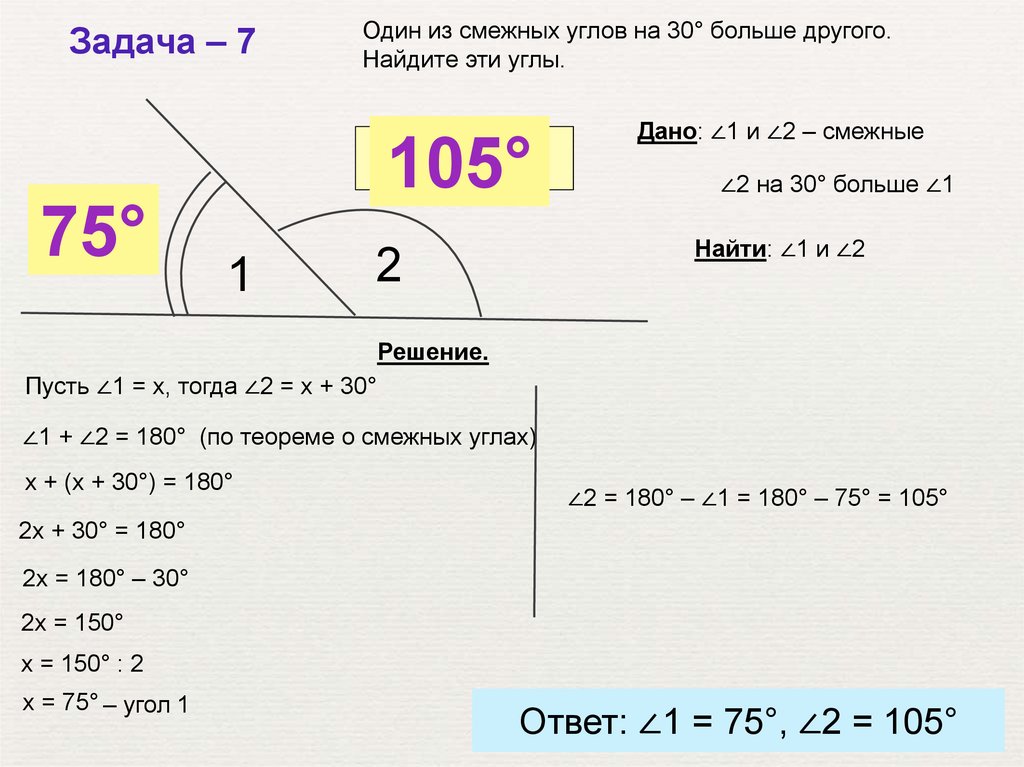
Задача – 7Один из смежных углов на 30° больше другого.
Найдите эти углы.
х+30°
105°
?
на 30° больше
x?
75°
1
Дано: ∠1 и ∠2 – смежные
∠2 на 30° больше ∠1
Найти: ∠1 и ∠2
2
Решение.
Пусть ∠1 = х, тогда ∠2 = х + 30°
∠1 + ∠2 = 180° (по теореме о смежных углах)
х + (х + 30°) = 180°
∠2 = 180° – ∠1 = 180° – 75° = 105°
2х + 30° = 180°
2х = 180° – 30°
2х = 150°
х = 150° : 2
х = 75° – угол 1
Ответ: ∠1 = 75°, ∠2 = 105°
9.
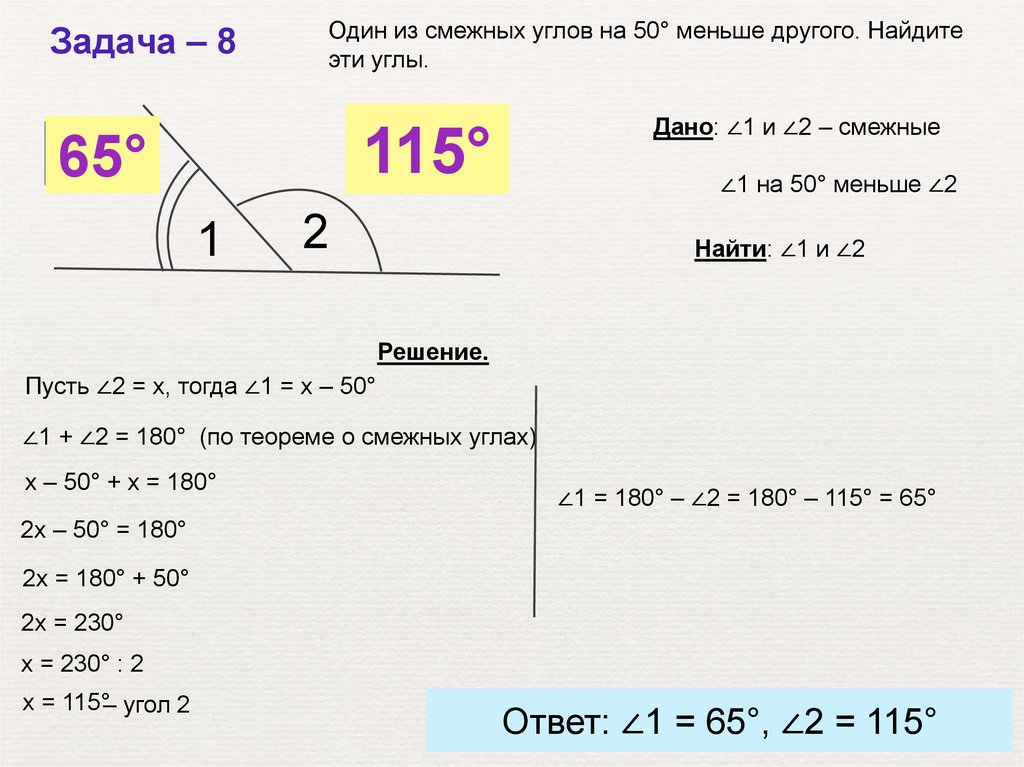
Задача – 8Один из смежных углов на 50° меньше другого. Найдите
эти углы.
на 50°
х–
50°
меньше
Дано: ∠1 и ∠2 – смежные
x
115°
?
65°
?
1
∠1 на 50° меньше ∠2
2
Найти: ∠1 и ∠2
Решение.
Пусть ∠2 = х, тогда ∠1 = х – 50°
∠1 + ∠2 = 180° (по теореме о смежных углах)
х – 50° + х = 180°
∠1 = 180° – ∠2 = 180° – 115° = 65°
2х – 50° = 180°
2х = 180° + 50°
2х = 230°
х = 230° : 2
х = 115°– угол 2
Ответ: ∠1 = 65°, ∠2 = 115°
10.
Задача – 9Смежные углы равны. Найдите эти углы.
Дано: ∠1 и ∠2 – смежные
∠1 = ∠2
?
1
?
2
Найти: ∠1 и ∠2
Решение.
∠1 и ∠2 – смежные, тогда по теореме о смежных углах имеем, что
∠1 + ∠2 = 180°.
По условию ∠1 = ∠2, тогда ∠1 = ∠2 = 180° : 2 = 90°
Ответ: ∠1 = 90°, ∠2 = 90°
11.
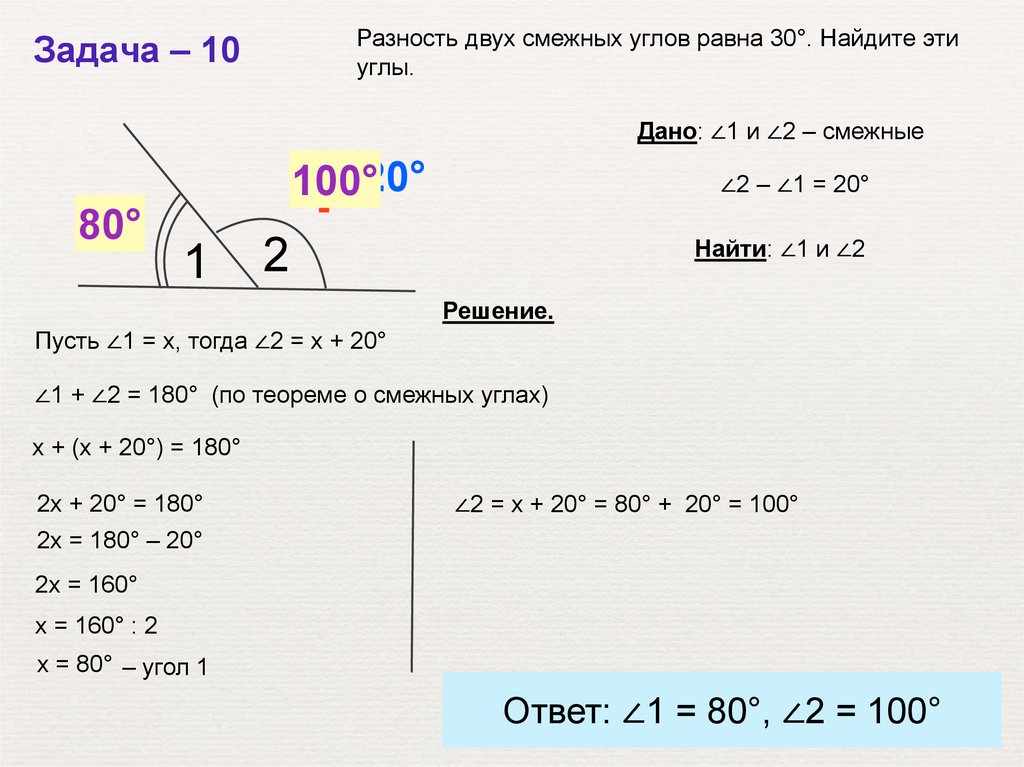
Разность двух смежных углов равна 30°. Найдите этиуглы.
Задача – 10
Дано: ∠1 и ∠2 – смежные
80°
х
? 1
?
x
+ 20°
100°
∠2 – ∠1 = 20°
Найти: ∠1 и ∠2
2
Решение.
Пусть ∠1 = х, тогда ∠2 = х + 20°
∠1 + ∠2 = 180° (по теореме о смежных углах)
х + (х + 20°) = 180°
2х + 20° = 180°
∠2 = х + 20° = 80° + 20° = 100°
2х = 180° – 20°
2х = 160°
х = 160° : 2
х = 80° – угол 1
Ответ: ∠1 = 80°, ∠2 = 100°
12.
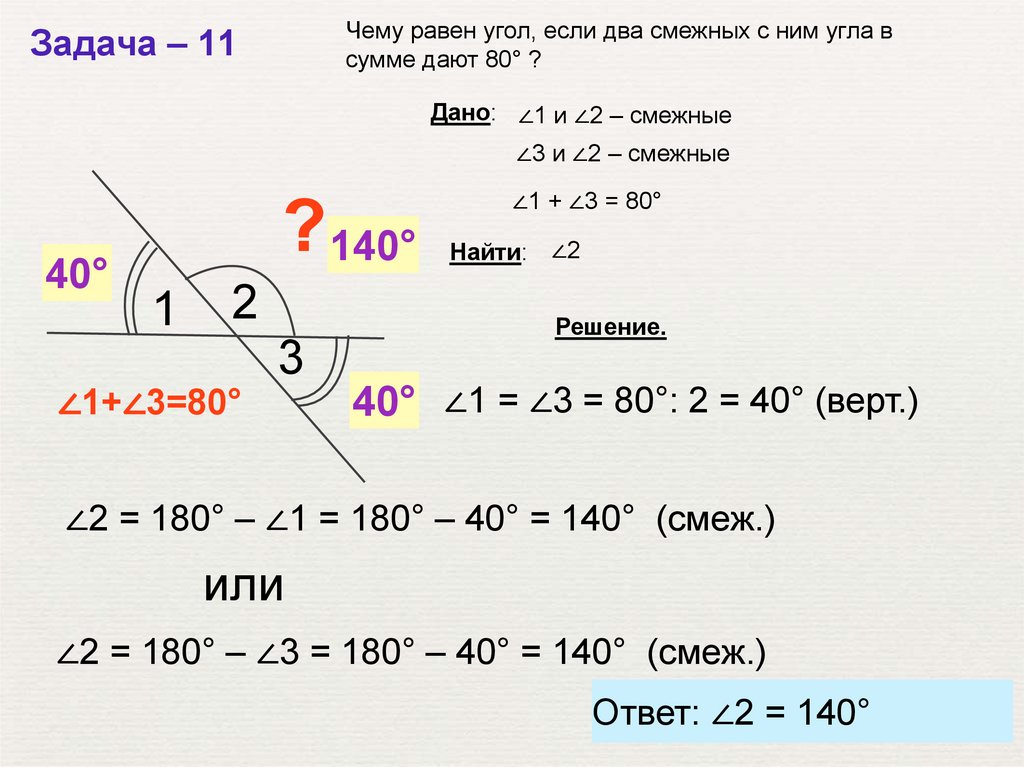
Чему равен угол, если два смежных с ним угла всумме дают 80° ?
Задача – 11
Дано: ∠1 и ∠2 – смежные
∠3 и ∠2 – смежные
40°
? 140°
1
2
3
∠1+∠3=80°
∠1 + ∠3 = 80°
Найти: ∠2
Решение.
40° ∠1 = ∠3 = 80°: 2 = 40° (верт.)
∠2 = 180° – ∠1 = 180° – 40° = 140° (смеж.)
или
∠2 = 180° – ∠3 = 180° – 40° = 140° (смеж.)
Ответ: ∠2 = 140°
13.
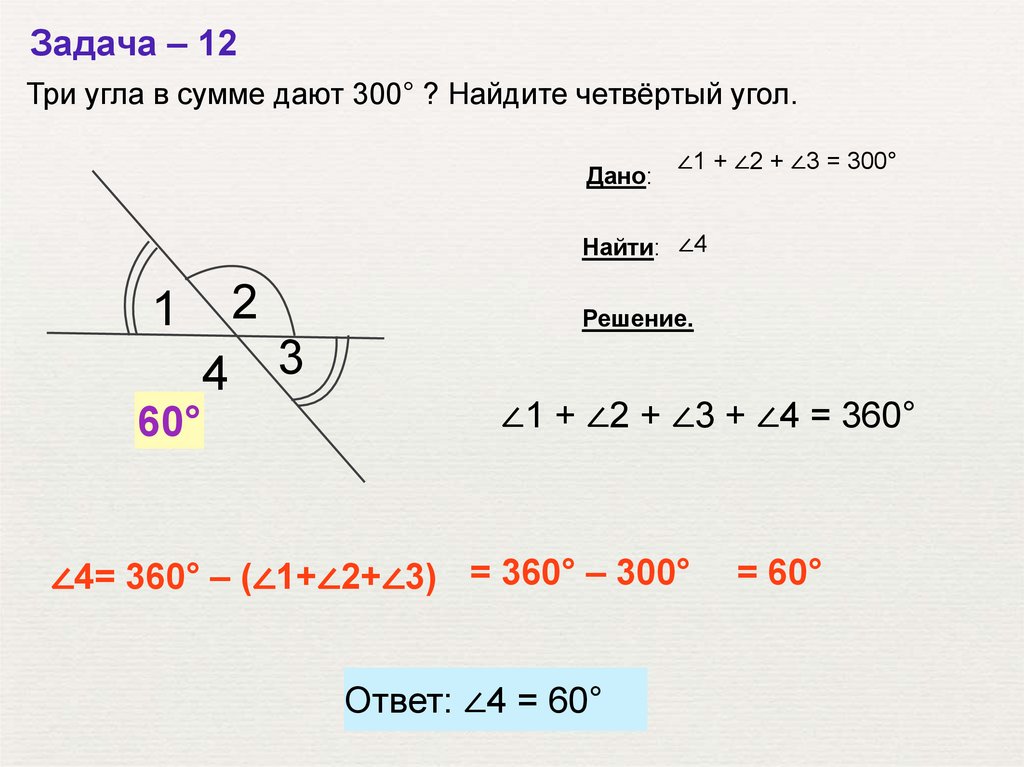
Задача – 12Три угла в сумме дают 300° ? Найдите четвёртый угол.
Дано:
∠1 + ∠2 + ∠3 = 300°
Найти: ∠4
2
1
4
?
60°
Решение.
3
∠1 + ∠2 + ∠3 + ∠4 = 360°
∠4= 360° – (∠1+∠2+∠3) = 360° – 300°
Ответ: ∠4 = 60°
= 60°
14.
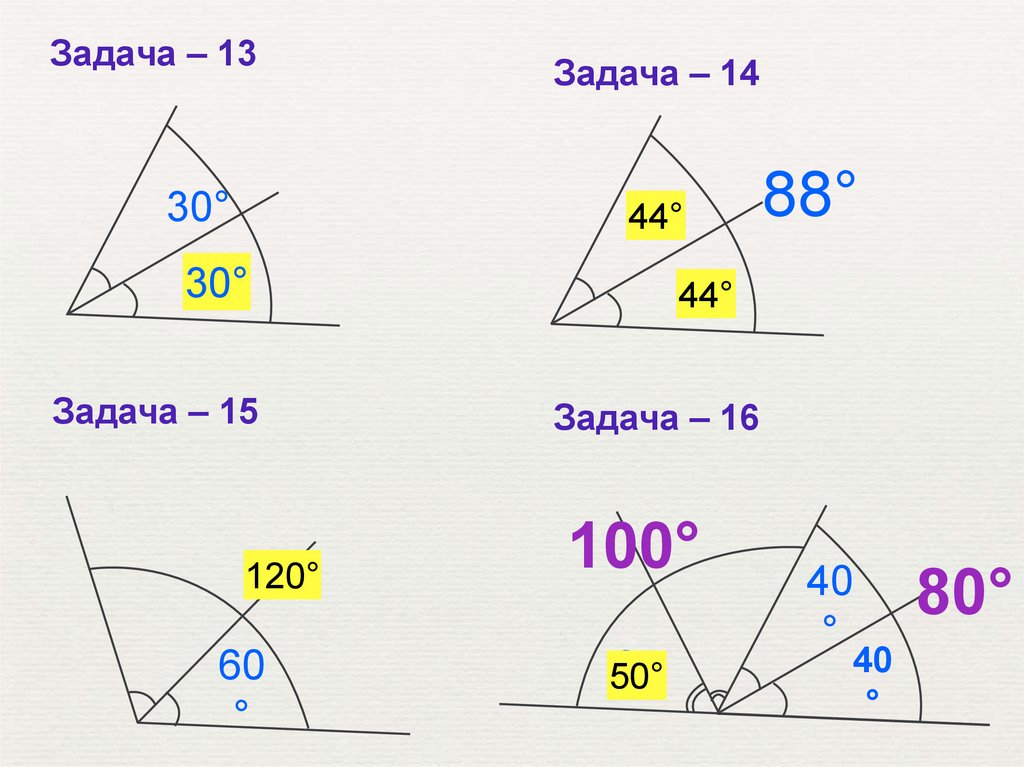
Задача – 13Задача – 14
30°
44°
?
30°
?
88°
44°
?
Задача – 15
Задача – 16
?
120°
60
°
100°
?
50°
40
°
40
°
80°
15.
ДЗ1.<ABC = 600 . Найти <CBD, смежный с ним.
2. Один из смежных углов в 2 раза больше другого, найти эти углы.
3. Один из смежных углов в 3 раза больше другого, найти эти углы.
4. Один из смежных углов в 4 раза больше другого, найти эти углы.
5. Один из смежных углов в 5 раз больше другого, найти эти углы.
6. Один из смежных углов на 400 больше другого, найти эти углы.
7. Один из смежных углов на 1000 больше другого, найти эти углы.
8. Один из смежных углов на 100 больше другого, найти эти углы.






 mathematics
mathematics