Сила гидростатического давления на плоские поверхности (тема 2)

1.

МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное учреждение высшего образования
Санкт-Петербургский государственный архитектурно-строительный университет
Тема 2.
Сила гидростатического
давления на плоские
поверхности
Санкт-Петербург 2020
Дисциплина:
Механика жидкости и газа
Преподаватель:
Феськова Алина Яновна

2.

При расчете строительных конструкций и сооружений необходимо
знать общую силу давления жидкости на сооружение или его
часть, а не только силу давления в отдельной точке.
C – центр тяжести смоченной конструкции
Pх
D – центр давления смоченной конструкции
F – сила давления жидкости
hC
hD
F
С
lC
hC – глубина погружения центра тяжести (от
поверхности жидкости до точки С)
e
lD
hD – глубина погружения центра давления (от
поверхности жидкости до точки D)
D
α
lC – расстояние от поверхности жидкости до точки C
lD – расстояние от поверхности жидкости до точки D
α – угол наклона конструкции или сооружения
Pх – давление на поверхности жидкости
e – эксцентриситет

3.

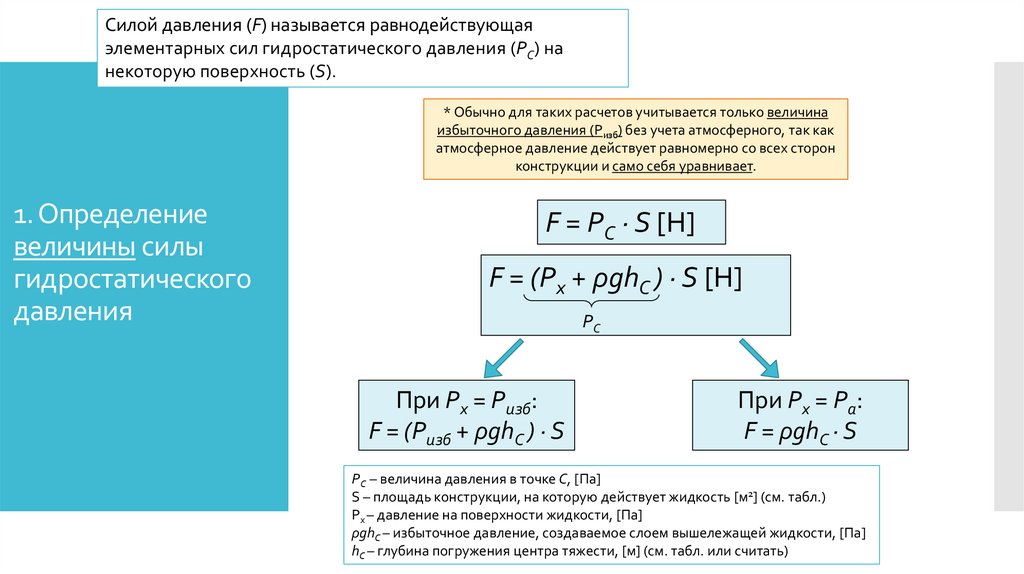
Силой давления (F) называется равнодействующая
элементарных сил гидростатического давления (PC) на
некоторую поверхность (S).
* Обычно для таких расчетов учитывается только величина
избыточного давления (Pизб) без учета атмосферного, так как
атмосферное давление действует равномерно со всех сторон
конструкции и само себя уравнивает.
1. Определение
величины силы
гидростатического
давления
F = PC ∙ S [Н]
F = (Pх + ρghC ) ∙ S [Н]
PC
При Px = Pизб:
F = (Pизб + ρghC ) ∙ S
При Px = Pа:
F = ρghC ∙ S
PC – величина давления в точке С, [Па]
S – площадь конструкции, на которую действует жидкость [м2] (см. табл.)
Px – давление на поверхности жидкости, [Па]
ρghC – избыточное давление, создаваемое слоем вышележащей жидкости, [Па]
hC – глубина погружения центра тяжести, [м] (см. табл. или считать)

4.

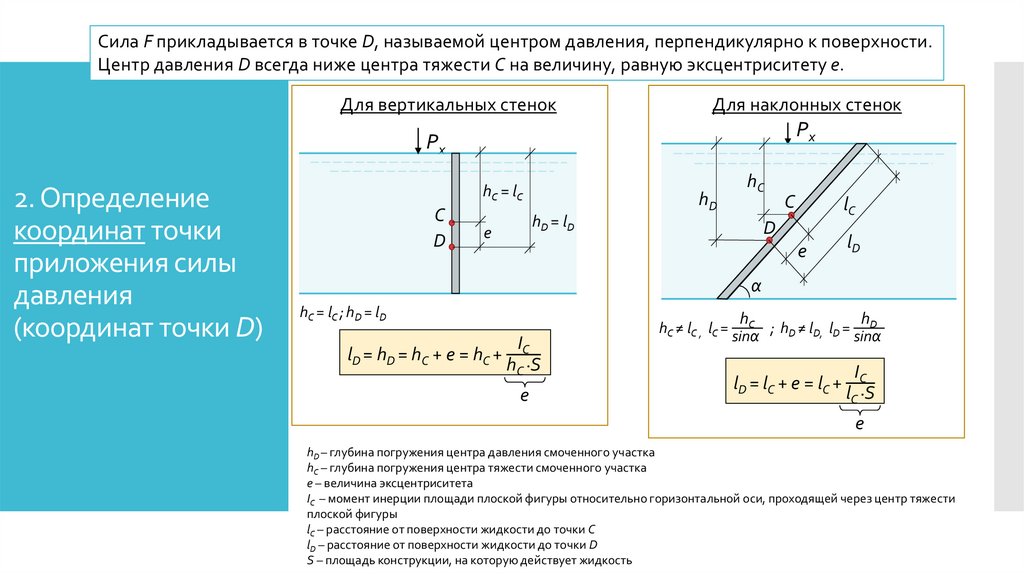
Сила F прикладывается в точке D, называемой центром давления, перпендикулярно к поверхности.
Центр давления D всегда ниже центра тяжести C на величину, равную эксцентриситету e.
Для вертикальных стенок
Для наклонных стенок
Pх
Pх
2. Определение
координат точки
приложения силы
давления
(координат точки D)
hC = lC
С
D
hD
hC
hD = lD
e
С
lC
D
e
lD
α
hC = lC ; hD = lD
lD = hD = hC + e = hC +
IC
hC ∙S
e
hC ≠ lC , lC =
hC
h
; hD ≠ lD, lD = D
sinα
sinα
lD = lC + e = lC +
IC
lC ∙S
e
hD – глубина погружения центра давления смоченного участка
hC – глубина погружения центра тяжести смоченного участка
e – величина эксцентриситета
IC – момент инерции площади плоской фигуры относительно горизонтальной оси, проходящей через центр тяжести
плоской фигуры
lC – расстояние от поверхности жидкости до точки C
lD – расстояние от поверхности жидкости до точки D
S – площадь конструкции, на которую действует жидкость

5.

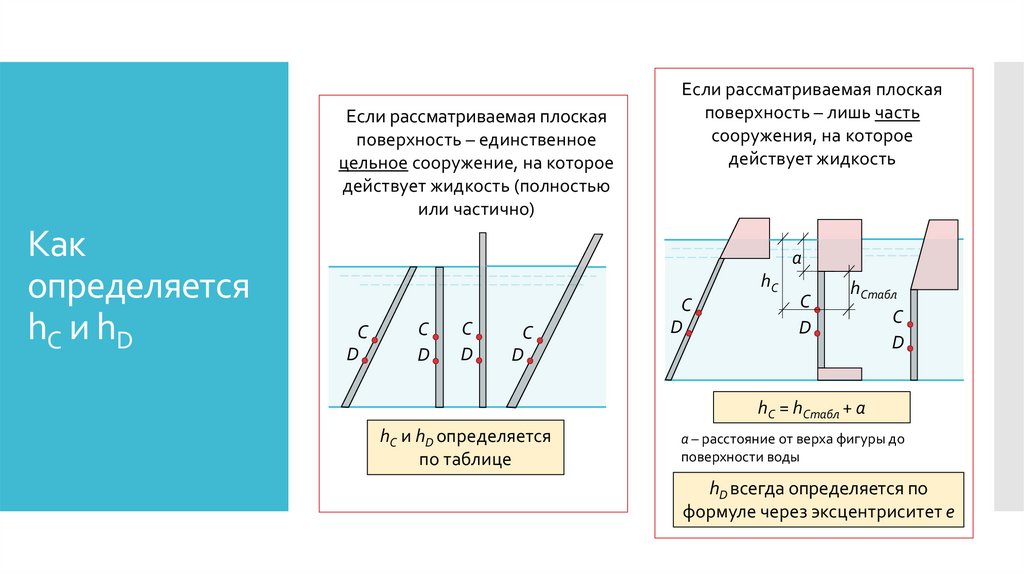
Если рассматриваемая плоская
поверхность – единственное
цельное сооружение, на которое
действует жидкость (полностью
или частично)
Как
определяется
hC и hD
Если рассматриваемая плоская
поверхность – лишь часть
сооружения, на которое
действует жидкость
а
hC
С
D
С
D
С
D
С
D
С
D
С
D
hCтабл
С
D
hC = hCтабл + a
hC и hD определяется
по таблице
a – расстояние от верха фигуры до
поверхности воды
hD всегда определяется по
формуле через эксцентриситет e

6.

Сечение
hC
hD
h
C
D
S
IC
hC
hD
bh
bh3
12
h
2
2h
3
bh
2
bh3
36
2h
3
3h
4
h
2 (a + b)
h3 (a2 + 4ab + b2)
36 (a + b)
h (a + 2b)
3 ∙ (a + b)
πr4
πD4
4 или 64
D
r или 2
5
5
R
или
4
8D
πa3b
4
a
5
4a
R
(R2 + r2)
R+
4R
b
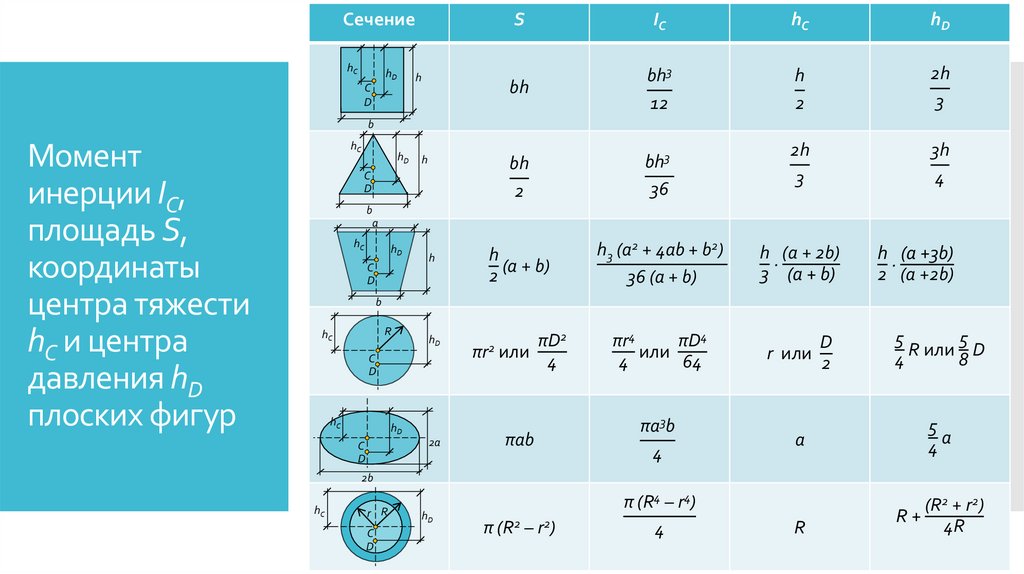
Момент
инерции IC,
площадь S,
координаты
центра тяжести
hC и центра
давления hD
плоских фигур
hC
hD
h
C
D
b
a
hC
hD
C
D
h
h (a +3b)
2 ∙ (a +2b)
b
R
hC
hD
4
C
D
hC
hD
2a
C
D
πD
πr2 или
πab
2
2b
hC
r R
C
D
hD
π (R2 – r2)
π (R4 – r4)
4

7.

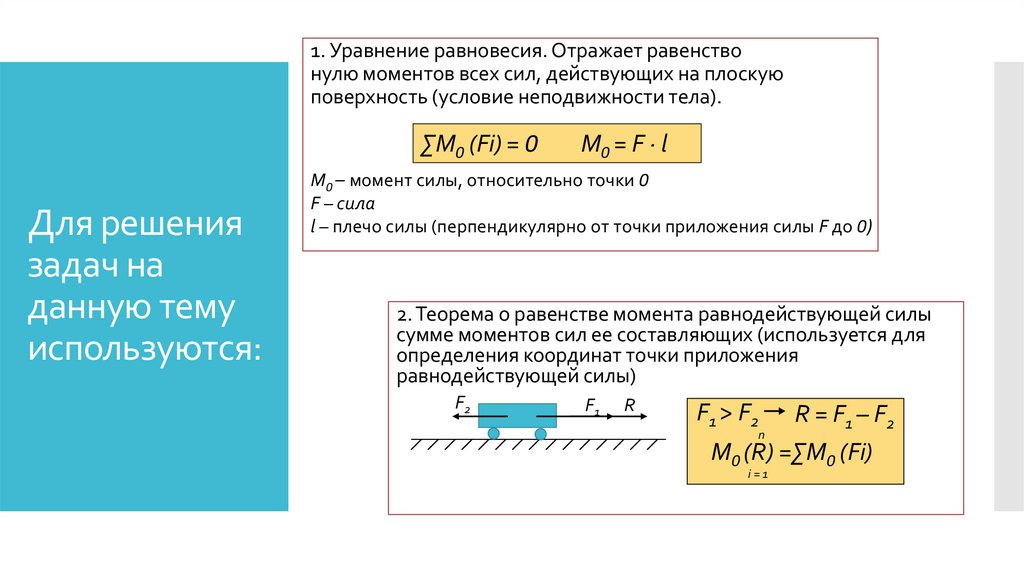
1. Уравнение равновесия. Отражает равенство
нулю моментов всех сил, действующих на плоскую
поверхность (условие неподвижности тела).
∑М0 (Fi) = 0
Для решения
задач на
данную тему
используются:
М0 = F ∙ l
М0 – момент силы, относительно точки 0
F – сила
l – плечо силы (перпендикулярно от точки приложения силы F до 0)
2. Теорема о равенстве момента равнодействующей силы
сумме моментов сил ее составляющих (используется для
определения координат точки приложения
равнодействующей силы)
F2
F1
R
F1 > F2
R = F 1 – F2
n
М0 (R) =∑М0 (Fi)
i=1