Similar presentations:
Сила давления жидкости на плоские и криволинейные стенки
1.
СИЛА ДАВЛЕНИЯ ЖИДКОСТИНА ПЛОСКИЕ И КРИВОЛИНЕЙНЫЕ
СТЕНКИ
Лекция 2
2.
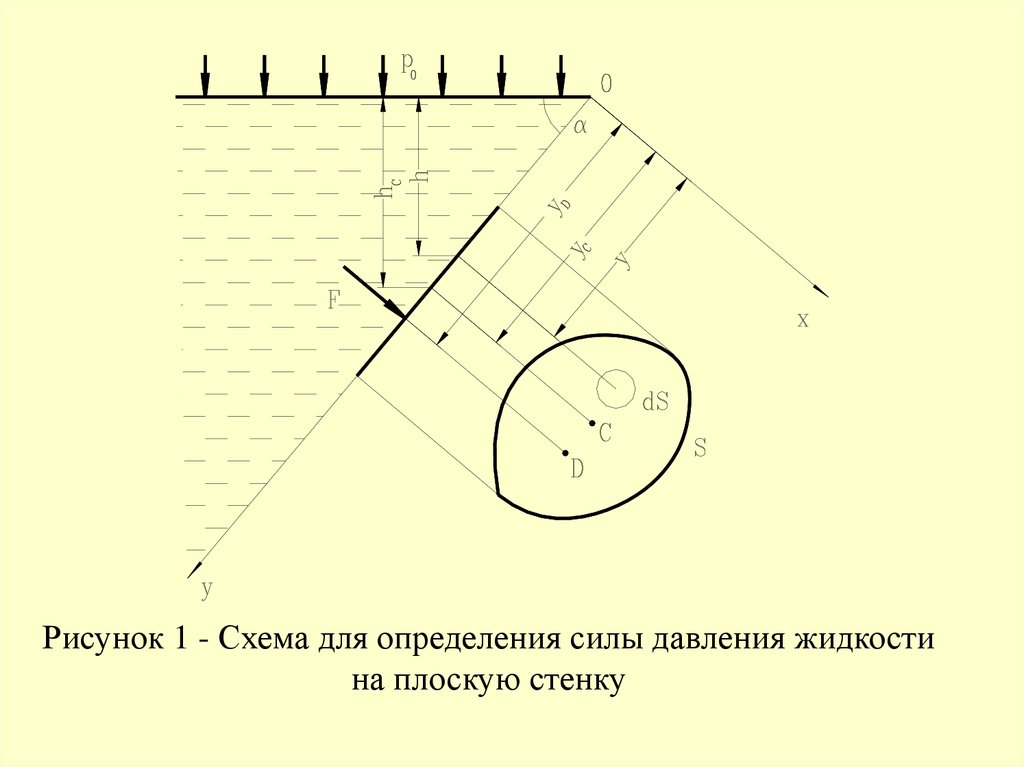
1. Сила давления жидкости на плоскую стенкуНайдем силу давления жидкости на плоскую
стенку площадью S, расположенную под
произвольным углом к горизонту и ограниченную
произвольным контуром (рис.1).
Сила характеризуется тремя параметрами:
– направлением:
– величиной;
– точкой приложения.
3.
Рисунок 1 - Схема для определения силы давления жидкостина плоскую стенку
4.
Давление в каждой точке стенки направлено понормали к ней, следовательно, и равнодействующая сила
давления будет перпендикулярна плоской стенке.
Ось 0x направим по линии пересечения стенки со
свободной поверхностью жидкости, а ось 0y –
перпендикулярно к этой линии в плоскости стенки.
Вычислим элементарную силу давления,
приложенную к бесконечно малой площадке dS:
dF p dS p0 g h dS p0 dS g hdS
где p0 – давление на свободную поверхность;
h – глубина расположения площадки dS.
5.
Для получения полной силы давления F проинтегрируемполученное выражение по всей площади S:
F p0 dS g hdS p0 S g sin ydS
S
S
S
Полученный интеграл представляет собой статический
момент площади S относительно оси 0x и равен произведению этой
площади на координату ее центра масс (точка С), то есть
y dS yC S
Следовательно,
S
F p0 S g sin yC S p0 S g hC S
p0 g hC S pC S
где hC, pC – глубина расположения центра масс площадки и
давление в этой точке.
6.
Таким образом, полная сила давления жидкости наплоскую стенку равна произведению площади стенки на
гидростатическое давление pC в центре масс этой
площади.
При давлении на свободную поверхность, отличном от
нормального (атмосферного), сила давления на поверхность
стенки определяется по выражению
F pC p ман. S
или F pC pвак. S
где рман. и рвак. – манометрическое и вакуумметрическое давление
7.
Найдем точку приложения силы давления наплоскую стенку.
Сила F0 будет приложена в центре масс плоской стенки C,
так как давление p0 действует на все точки стенки одинаково.
Точка приложения силы Fж находится путем составления
уравнения моментов равнодействующей и составляющих сил
относительно горизонтальной оси, например, совпадающей с
линией пересечения стенки со свободной поверхностью:
Fс yD ydFс
S
8.
Выразим координату точки приложения силы yD и2
подставим значения сил Fж и dFж:
g sin y dS
Jx
yD
g sin yC S
yC S
S
где –
оси 0x.
2
J x y dS
S
Учитывая, что
момент инерции площади S относительно
J x J x0
2
yC S
где Jx0 – момент инерции площади S относительно горизонтальной
оси, лежащей в плоскости стенки и проходящей через ее центр
масс.
Отсюда, точка приложения силы Fж имеет координату
J x0
yD yC
yC S
ИЛИ
J x0
hD hC
hC S
9.
2. Сила давления жидкости на криволинейныестенки
Если поверхность имеет произвольную форму, то
требуется находить 3 составляющих силы и 3 момента.
Чаще рассматривают цилиндрические и сферические
поверхности, имеющие вертикальную плоскость
симметрии. Возьмем цилиндрическую поверхность (рис.
2) с образующей, перпендикулярной плоскости рисунка
и определим силу давления на эту поверхность в двух
случаях:
– жидкость расположена сверху;
– жидкость расположена снизу.
10.
zy
x
Fx
α
Fz
F
Рисунок 2 - Схема для определения силы давления
жидкости на криволинейную (цилиндрическую)
поверхность
11.
На рисунке показана реакция стенки на жидкость,которая, как известно, равна силе давления жидкости на стенку
(по третьему закону Ньютона). Рассмотрим условия
равновесия объема жидкости ABDE, лежащей строго над
интересующей нас криволинейной поверхностью. Условие
равновесия в вертикальном направлении
Fz = ρgVт.д.,
где Vт.д. – объем тела давления;
Объем тела давления – это объем жидкости,
ограниченный рассматриваемой стенкой и вертикальной
проекцией, проведенной через контур рассматриваемой
стенки.
Условие равновесия в горизонтальном направлении:
Fx = g hC Szy.
где Szy – площадь проекции стенки на вертикальную
плоскость zOy
12.
По вычисленным составляющим Fz и Fx найдемвеличину силы давления жидкости на стенку
2
2
F Fx Fz
Угол наклона силы давления к горизонтальной
плоскости
F
arctg
z
Fx
.











 physics
physics








