Нахождение моды и медианы

1.

Контрольная работа
по статистике
вариант №….
Шрифт Time Roman, 12
Интервал 1,0
Поля везде 2,0

2.

ЗАДАНИЕ 2
Средние величины

3.

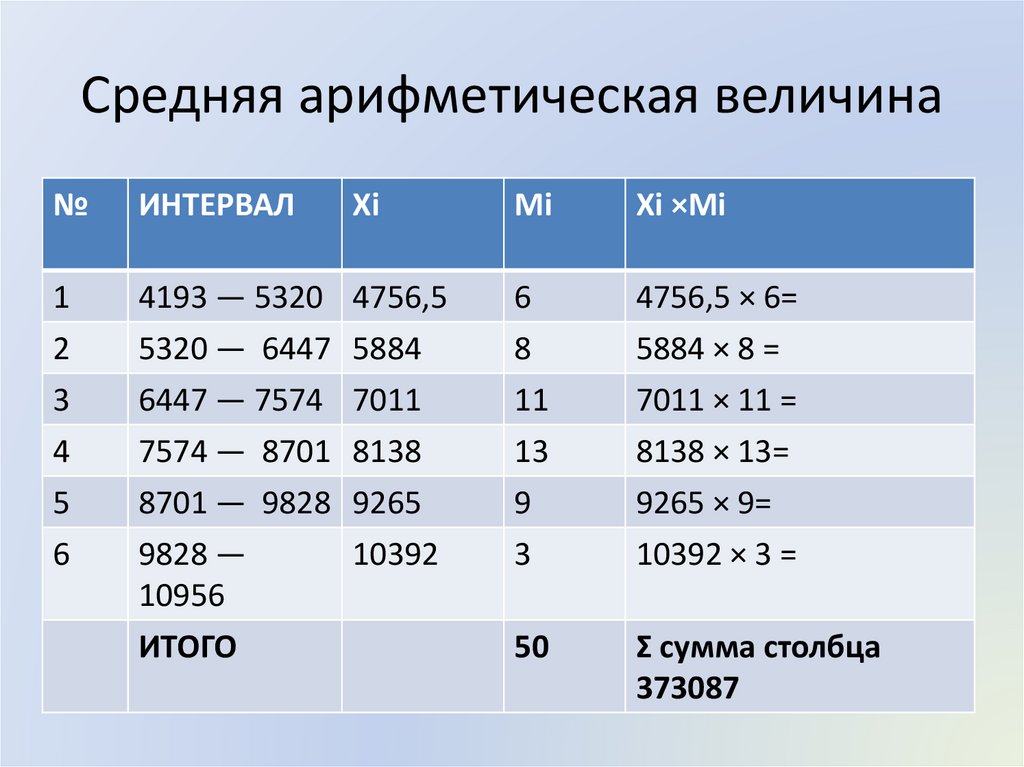
Средняя арифметическая величина
№
ИНТЕРВАЛ
1
2
Xi
Mi
Xi ×Mi
4193 — 5320 4756,5
5320 — 6447 5884
6
8
4756,5 × 6=
5884 × 8 =
3
4
5
6447 — 7574 7011
7574 — 8701 8138
8701 — 9828 9265
11
13
9
7011 × 11 =
8138 × 13=
9265 × 9=
6
9828 —
10956
ИТОГО
3
10392 × 3 =
50
Σ сумма столбца
373087
10392

4.

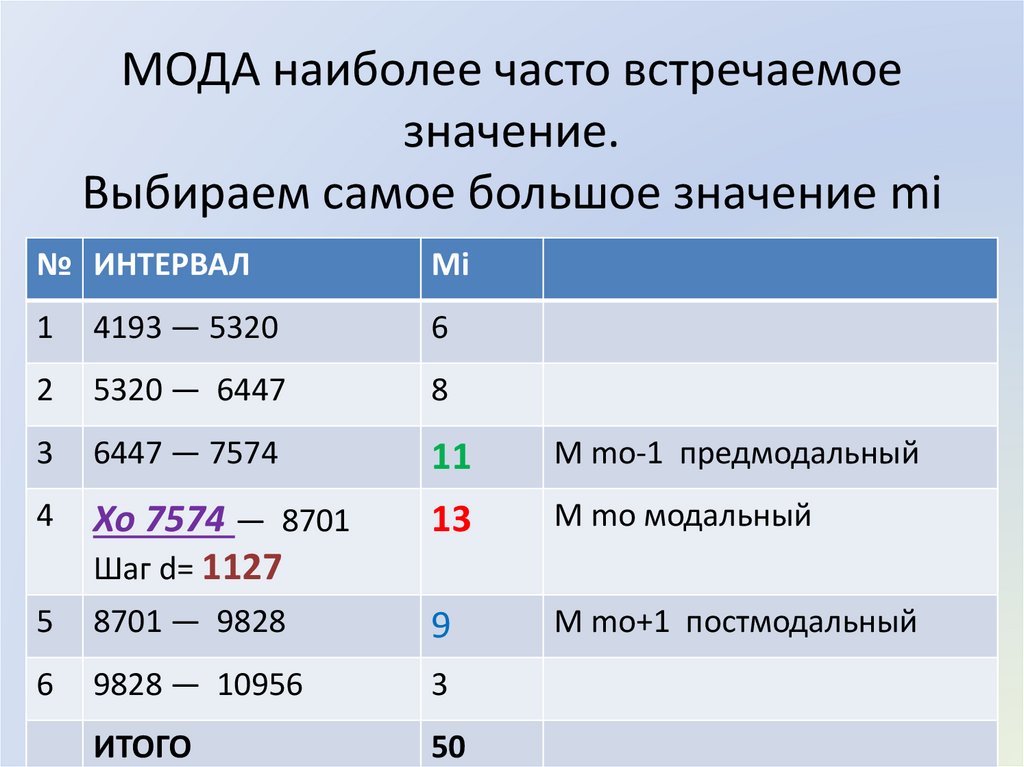
МОДА наиболее часто встречаемое
значение.
Выбираем самое большое значение mi
№ ИНТЕРВАЛ
Mi
1
4193 — 5320
6
2
5320 — 6447
8
3
6447 — 7574
11
M mo-1 предмодальный
4
Хо 7574 — 8701
Шаг d= 1127
13
M mo модальный
5
8701 — 9828
9
M mo+1 постмодальный
6
9828 — 10956
3
ИТОГО
50

5.

ПОДСТАНОВКА
Мо= Х0 (7575) + d (1127) × (13-11)/(13-11)+(13-9)
Чтобы избежать типичную ошибку нужно:
Первое действие - просчитать дробь!!!!!
Второе действие – умножить!!!!!
Третье действие – сложить с Хо.
Самопроверка: Полученное число должно
попасть в модальный интервал!!!!!

6.

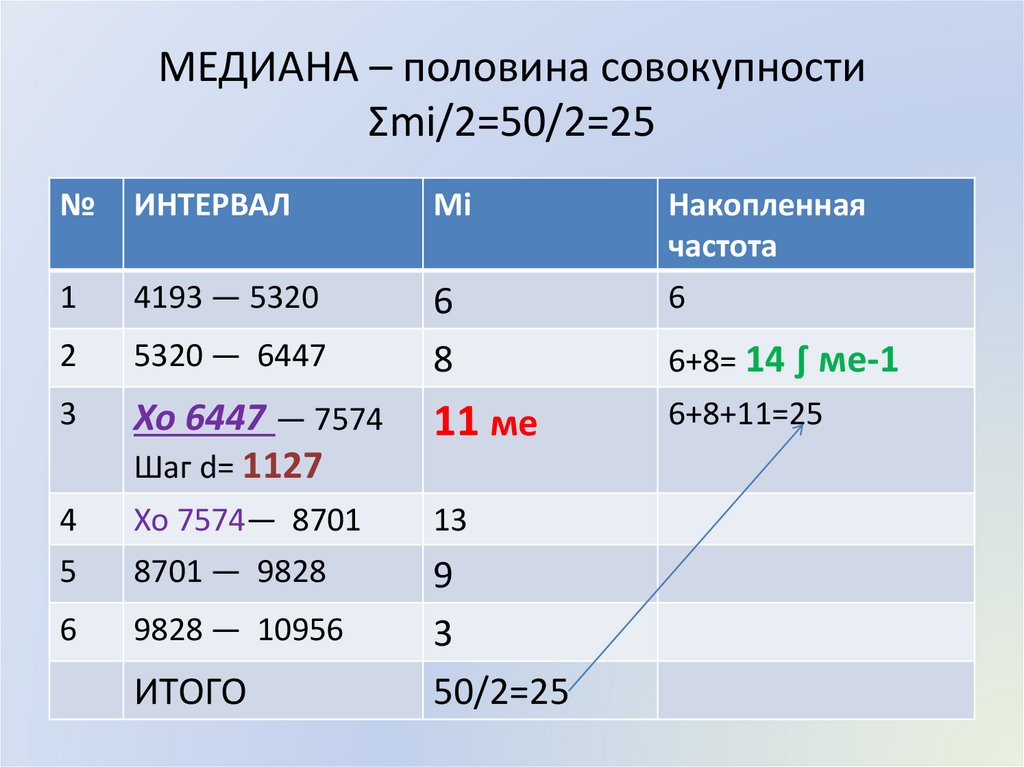
МЕДИАНА – половина совокупности
Σmi/2=50/2=25
№
ИНТЕРВАЛ
Mi
1
4193 — 5320
2
5320 — 6447
6
8
3
Хо 6447 — 7574
Шаг d= 1127
11 ме
4
5
Хо 7574— 8701
8701 — 9828
13
6
9828 — 10956
ИТОГО
9
3
50/2=25
Накопленная
частота
6
6+8= 14 ∫ ме-1
6+8+11=25

7.

ПОДСТАНОВКА
• Ме= Х0 (6447) + d (1127) × (25-14)/11
Чтобы избежать типичную ошибку нужно:
Первое действие - просчитать дробь!!!!!
Второе действие – умножить!!!!!
Третье действие – сложить с Хо.
Самопроверка: Полученное число должно
попасть в медианный интервал!!!!!

8.

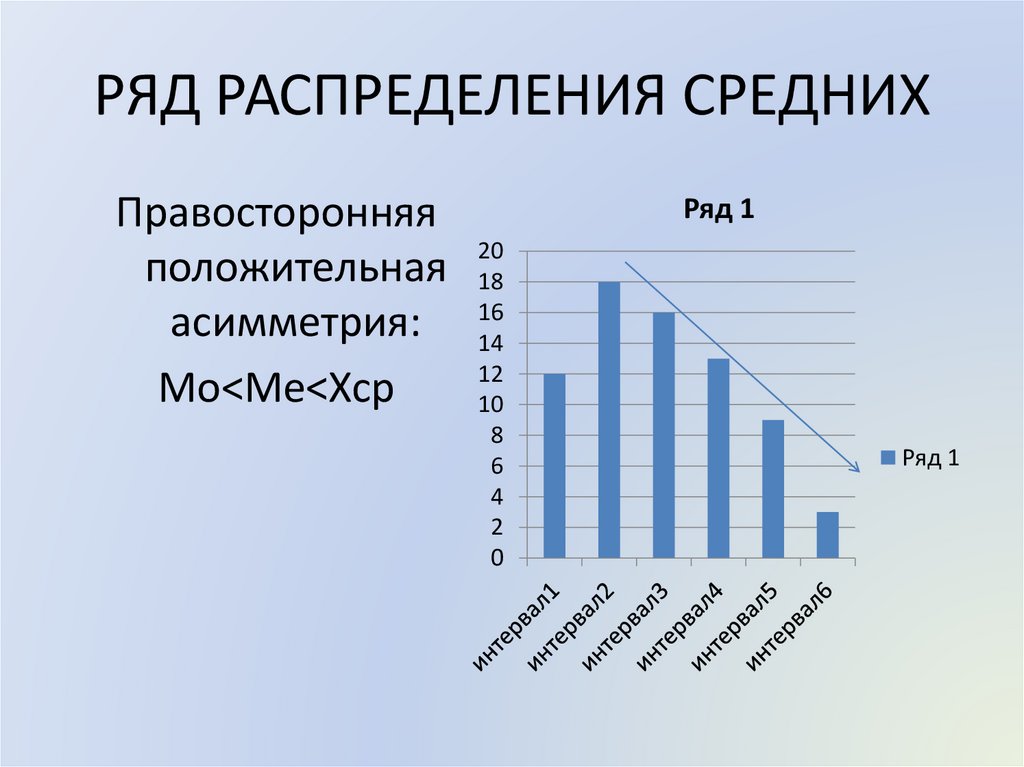
РЯД РАСПРЕДЕЛЕНИЯ СРЕДНИХ
Правосторонняя
20
положительная 18
асимметрия: 16
14
12
Мо<Ме<Хср
10
8
6
4
2
0
Ряд 1
Ряд 1

9.

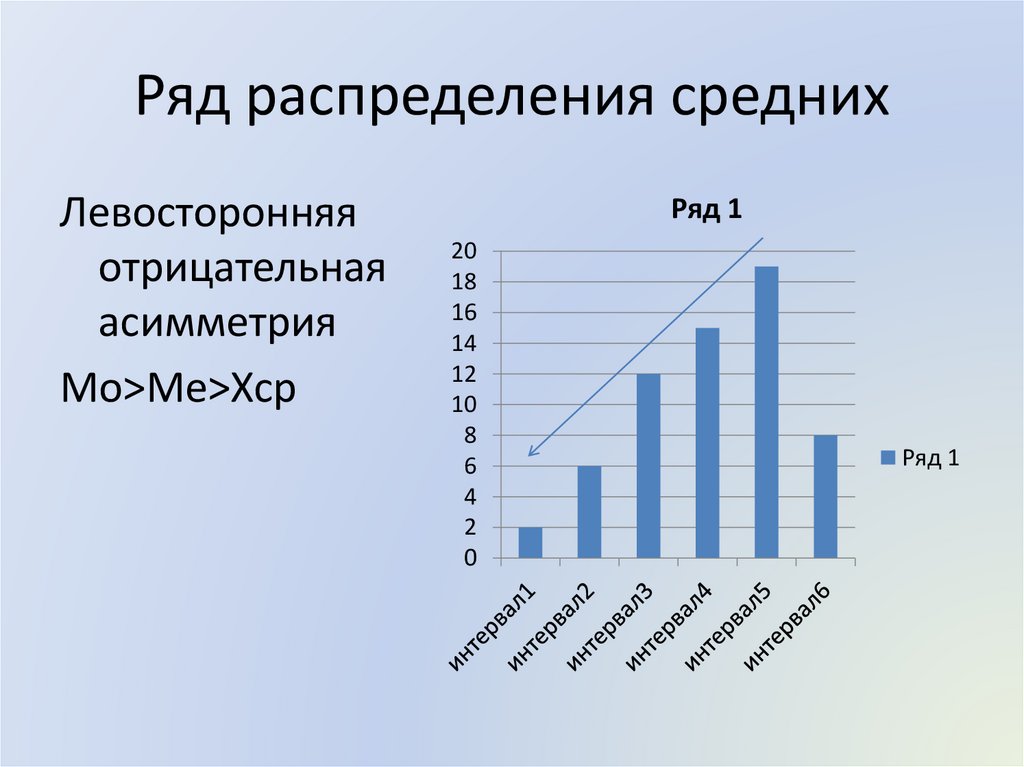
Ряд распределения средних
Левосторонняя
отрицательная
асимметрия
Мо>Ме>Хср
Ряд 1
20
18
16
14
12
10
8
6
4
2
0
Ряд 1