Структурные средние величины. Мода и медиана

1.

Структурные средние
величины
Мода и медиана.
© Фокина Лидия Петровна

2.

Наиболее часто используемые в
экономической практике
структурными характеристиками
являются мода и медиана.
© Фокина Лидия Петровна

3.

Мода – значение изучаемого признака,
повторяющегося с наибольшей частотой.
M0
xM
0
i
M0
fM
fM
f
M 0 1
0
f
0
M 0 1
fM
f
M 0 1
где XM0 – нижняя граница модального интервала,
iM0 – величина модального
fM
0
интервала,
– частота, соответствующая модальному
интервалу,
fM
fM
© Фокина Лидия Петровна
0 1
– частота предшествующего интервала,
– частота интервала, следующего за модальным.
0 1

4.

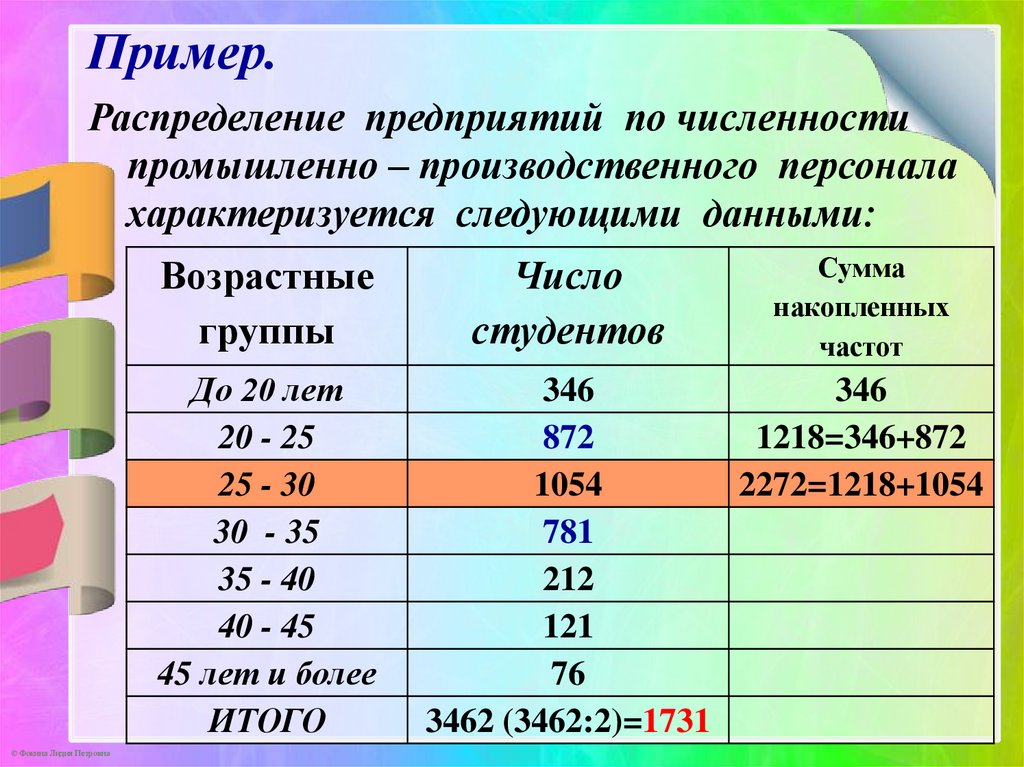
Пример.
Распределение предприятий по численности
промышленно – производственного персонала
характеризуется следующими данными:
Возрастные
группы
До 20 лет
20 - 25
25 - 30
30 - 35
35 - 40
40 - 45
45 лет и более
ИТОГО
© Фокина Лидия Петровна
Число
студентов
Сумма
накопленных
частот
346
346
872
1218=346+872
1054
2272=1218+1054
781
212
121
76
3462 (3462:2)=1731

5.

Решение:
Введем следующие обозначения:
x
MO
25, i M 5,
f
o
M o xM i M
Mo
1054,
f
f
M o 1
Mo
872,
f
f
M o 1
f
f
f
f
M
M
M
o
o 1
o
1054 872
25 5
27чел.
1054 872 1054 781
o
o
M o 1
781
M o 1
Вывод: одна половина студентов имеет возраст до 27
лет, а другая свыше 27 лет.
© Фокина Лидия Петровна

6.

© Фокина Лидия Петровна
Медиана – значение признака,
приходящееся на середину
ранжированной (упорядоченной)
совокупности.
Если ряд распределения дискретный и
имеет нечетное число членов, то
медианой будет варианта,
находящаяся в середине упорядоченного
ряда (упорядоченный ряд - это
расположение единиц совокупности в
возрастающем или убывающем
порядке).

7.

М е Х Ме
где
f
S M e 1
iM e 2
fMe
Х М е – нижняя граница медианного интервала;
iM e – медианный интервал;
f
– половина от общего числа наблюдений;
2
SM e 1 – сумма наблюдений, накопленная до начала
медианного интервала;
f M e – число наблюдений в медианном
интервале;
n 1
– номер медианы для нечетного числа
N Me
2
членов ряда; n – число членов ряда.
© Фокина Лидия Петровна

8.

Пример: имеется следующий
дискретный ряд распределения рабочих
по стажу работы. Определить медиану.
Стаж работы,
лет
Число
рабочих
Сумма накопленных
частот
10
12
15
2
6
16
17
20
Итого
12
4
40(40:2=20)
2
8 (8=6+2)
24(24=16+8)
чуть больше 20
Ответ: Медиана данного ряда 15 лет.
© Фокина Лидия Петровна

9.

Основное свойство медианы в том, что
сумма абсолютных отклонений
значений признака от медианы
меньше, чем от любой другой
величины.
© Фокина Лидия Петровна

10.

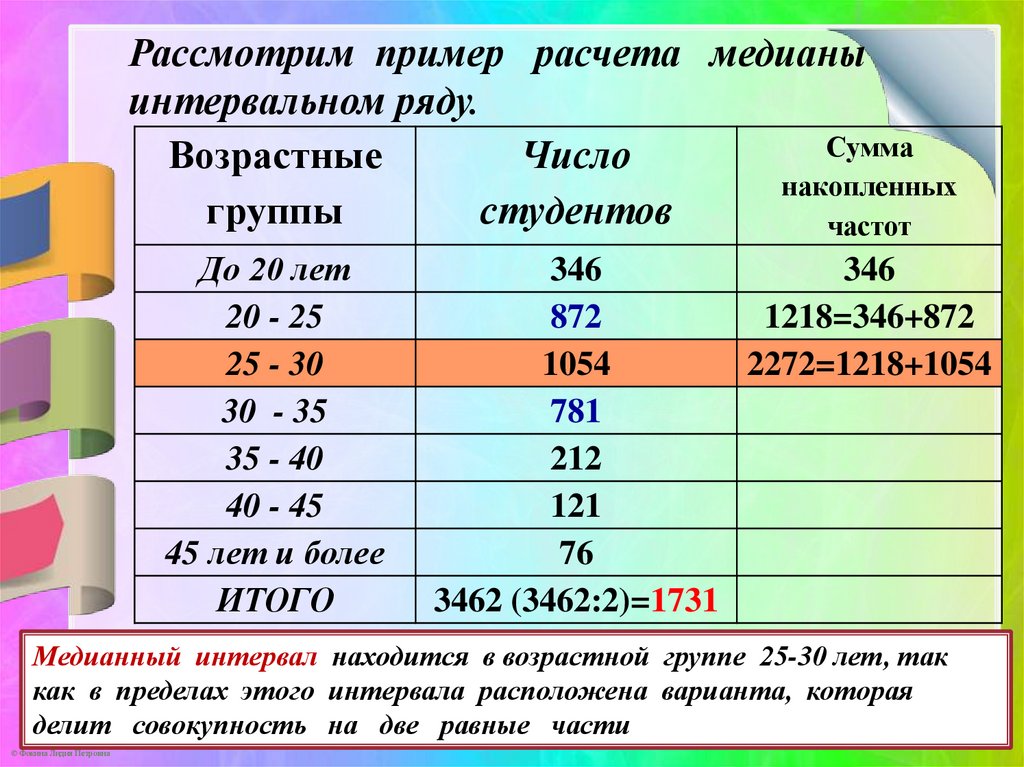
Рассмотрим пример расчета медианы
интервальном ряду.
Сумма
Возрастные
Число
накопленных
группы
студентов
частот
До 20 лет
20 - 25
25 - 30
30 - 35
35 - 40
40 - 45
45 лет и более
ИТОГО
346
346
872
1218=346+872
1054
2272=1218+1054
781
212
121
76
3462 (3462:2)=1731
Медианный интервал находится в возрастной группе 25-30 лет, так
как в пределах этого интервала расположена варианта, которая
делит совокупность на две равные части
© Фокина Лидия Петровна

11.

• Следовательно, этот интервал является
модальным интервала ряда распределения.
xM 25, i M 5, f M 1054,
f 1731,
1218,
S
M
2
е
е
е
e 1
Mе
1731 1218
25 5
27,4чел
1054
Ответ: Следовательно, половина студентов
возрастом меньше 27,4 года, а половина свыше 27,4
года.
© Фокина Лидия Петровна