Простейшие тригонометрические уравнения

1.

«Простейшие тригонометрические
уравнения»

2.

«Стоя на одном месте
новых горизонтов
не откроешь.»

3.

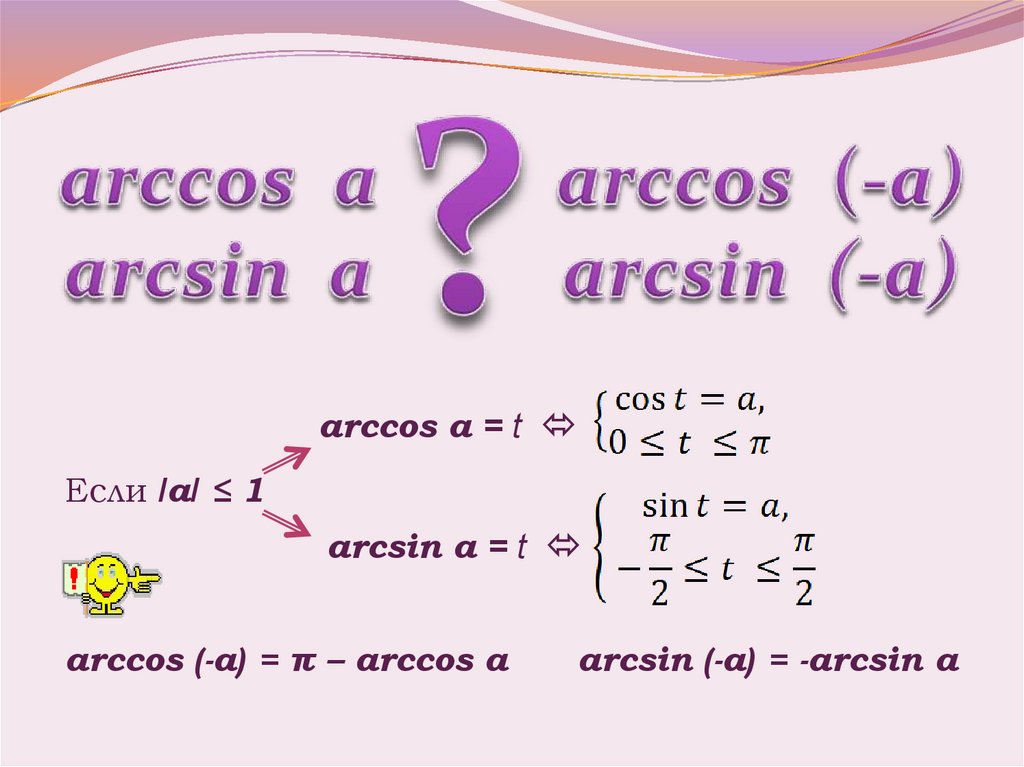
arccos a = t
Если ǀаǀ ≤ 1
arcsin a = t
arccos (-a) = π – arccos a
arcsin (-a) = -arcsin a

4.

Имеет ли смысл выражение?
Вычислите:

5.

Решите
уравнение:
Ответы:
корней нет

6.

7.

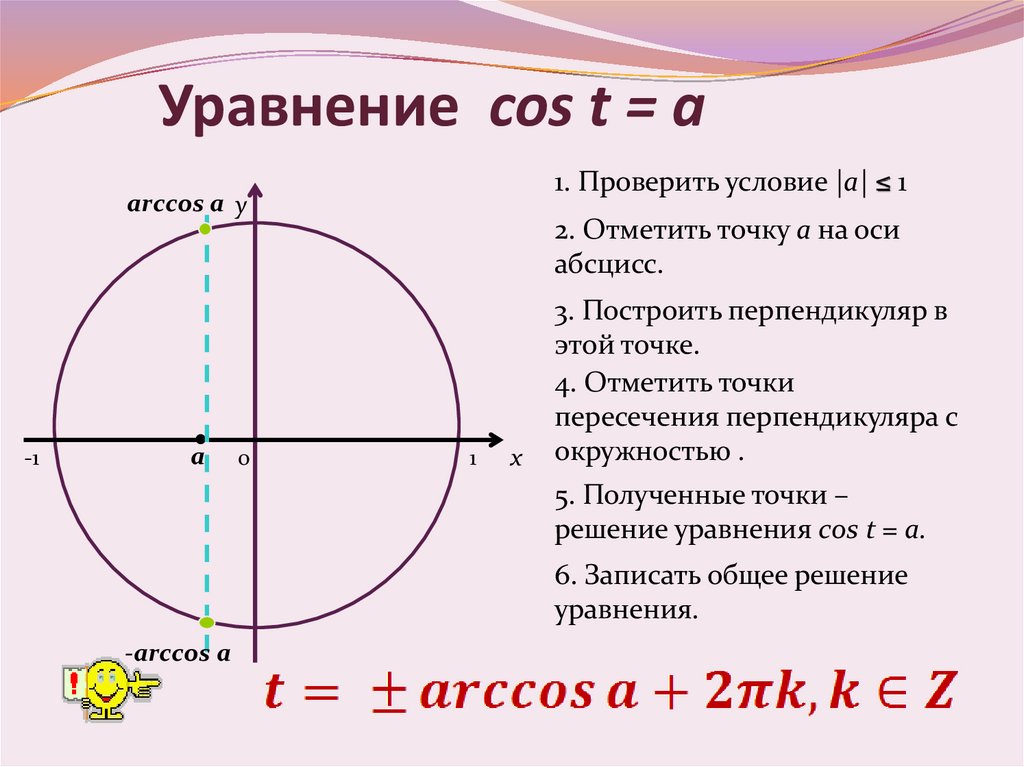
Уравнение cos t = a
1. Проверить условие |a| ≤ 1
arccos a y
-1
a
0
2. Отметить точку а на оси
абсцисс.
1
x
3. Построить перпендикуляр в
этой точке.
4. Отметить точки
пересечения перпендикуляра с
окружностью .
5. Полученные точки –
решение уравнения cos t = a.
6. Записать общее решение
уравнения.
-arccos a

8.

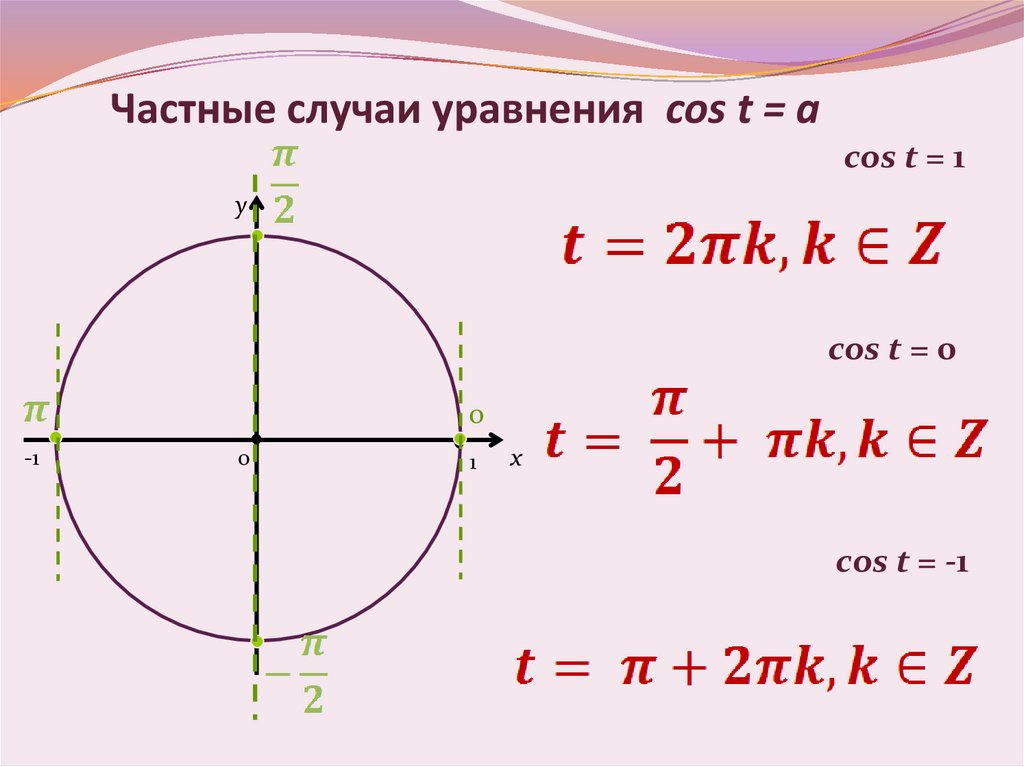
Частные случаи уравнения cos t = a
cos t = 1
y
cos t = 0
0
-1
0
1
x
cos t = -1

9.

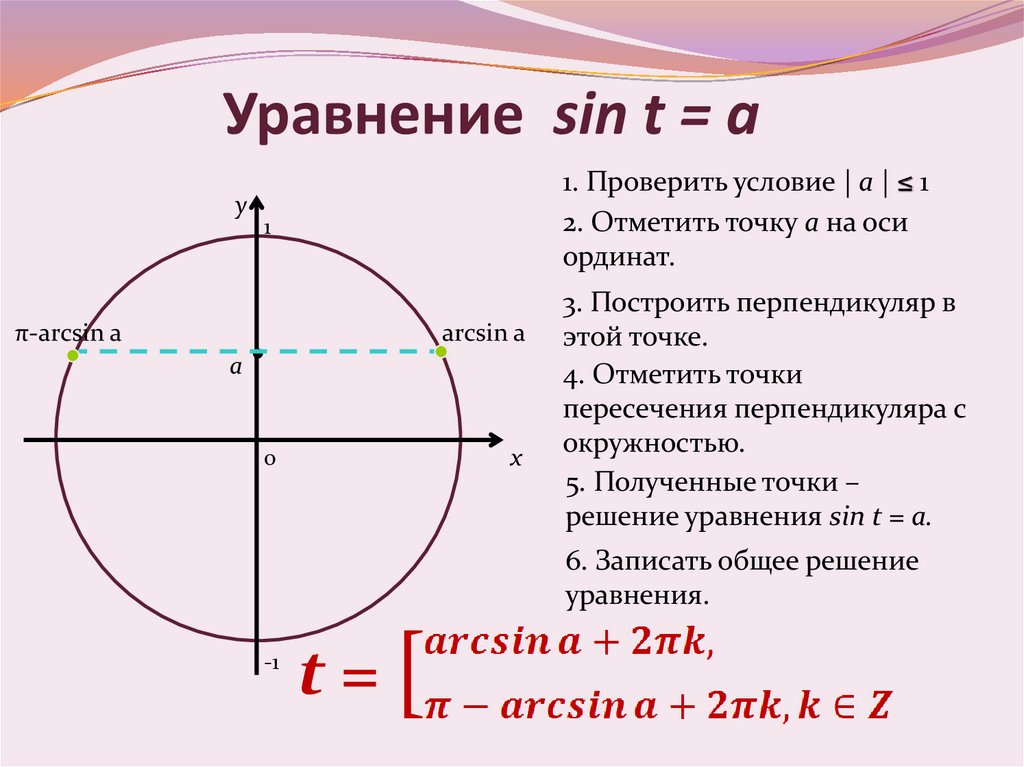
Уравнение sin t = a
y
1. Проверить условие | a | ≤ 1
2. Отметить точку а на оси
ординат.
1
π-arcsin a
arcsin a
a
x
0
3. Построить перпендикуляр в
этой точке.
4. Отметить точки
пересечения перпендикуляра с
окружностью.
5. Полученные точки –
решение уравнения sin t = a.
6. Записать общее решение
уравнения.
-1
t=[

10.

[

11.

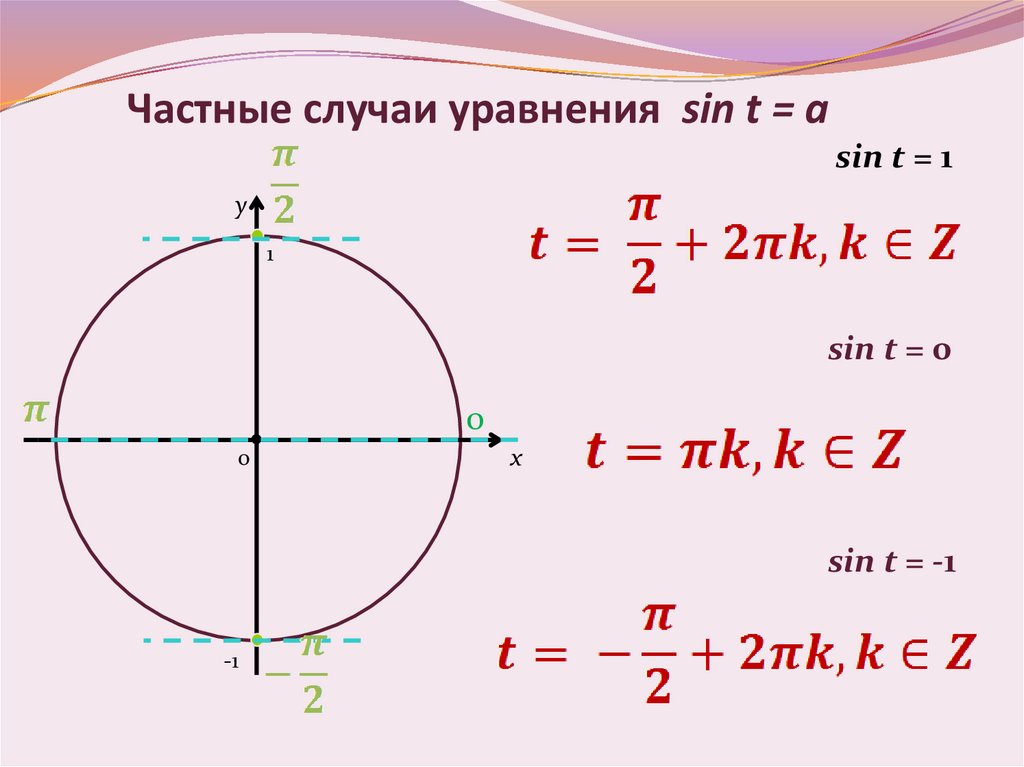
Частные случаи уравнения sin t = a
sin t = 1
y
1
sin t = 0
0
0
x
sin t = -1
-1

12.

Решите уравнения:
Сравните:

13.

Решите уравнение:

14.

cos t = a, ǀаǀ≤1
а) 2 sin х +