Применение систем линейных уравнений для решения прикладных задач

1.

Применение систем
линейных уравнений
для решения прикладных
задач.

2.

Математика –
царица наук
Карл Фридрих Гаусс

3.

Системы линейных уравнений
широко используются в
задачах экономики, физики,
электротехники,
программирования и других
наук.

4.

Уравнение называется линейным, если
оно содержит переменные только в
первой степени и не содержит
произведений переменных.
Система линейных уравнений с n
переменными:

5.

Числа aij
(i=1,2,…,m, j=1,2,…,n) называются
коэффициентами при переменных,
а bi (i=1,2,…,m) – свободными членами.
Решение системы уравнений — это
последовательность чисел (k1, k2, ..., kn),
которая является решением каждого
уравнения системы, т.е. при подстановке
в это уравнение вместо переменных
x1, x2,..., xn дает верное числовое равенство.

6.

Система, имеющая хотя бы
одно решение,
называется совместной;
система, не имеющая ни одного
решения — несовместной.
Методы решения:
По формулам Крамера;
Исключение неизвестных
( метод Гаусса);
С помощью обратной матрицы.

7.

Метод Крамера
Если главный определитель системы
то система имеет единственное решение, которое
можно найти по формулам Крамера:
где
–определитель, полученный из главного
заменой i-того столбца столбцом свободных
членов.

8.

Метод Гаусса
Это метод последовательного
исключения переменных, когда с помощью
элементарных преобразований система
уравнений приводится к равносильной системе
треугольного вида, из которой последовательно,
начиная с последних (по номеру), находятся все
переменные системы.
Расширенная матрица содержит вместе с
коэффициентами при неизвестных свободные
члены системы уравнений.

9.

Матричный метод
Cистему линейных уравнений записывают в
матричной форме: AX = B, где
A - основная матрица системы;
B - столбец свободных членов;
X - столбцы решений системы;
Матричное уравнение умножают слева на A–1
(матрицу, обратную к матрице A). Так как
A− 1A = E, то X = A -1B.
Метод применим, если определитель системы не
равен 0.

10.

Проверка домашнего задания
Решить систему линейных уравнений
всеми известными методами

11.

Применение систем линейных
уравнений
для решения прикладных задач.
Цель занятия:
формировать умение составлять
системы линейных уравнений по
текстовому условию задачи;
закрепить применение методов
Крамера и Гаусса решения систем
линейных уравнений.

12.

Доклад №1. Задача по электротехнике
Два источника постоянного
тока соединены
параллельно, имеют
E1=11,5 B, r1=2,5 Oм,
E1=16,5 B, r1=6 Oм,
и нагрузочный резистор
сопротивлением
Rн=30 Oм.
Определить значения и
направление токов через
источники и нагрузку.

13.

В соответствии со вторым законом Кирхгофа
Для контура, включающего в себя два
источника
и
имеем:
Для контура с источником
и
сопротивлением нагрузки
при обходе по
часовой стрелке имеем:
Подставив числовые данные, получим:

14.

Первое уравнение умножим на 6 и сложим со
вторым и третьим. Получим:
второе уравнение умножим на (-6) и сложим с
третьим. Получим:
Отсюда

15.

Доклад №2.
Из Москвы в Казань необходимо перевезти
оборудование трех типов:
I типа — 95 ед., II типа — 100 ед., III типа — 185 ед.
Для перевозки оборудования завод может заказать три
вида транспорта. Количество оборудования каждого
типа, вмещаемого на определенный вид транспорта,
приведено в таблице.
Тип
оборудования
I
II
III
Количество оборудования
Т1
Т2
Т3
3
2
1
4
1
2
3
5
4
Установить, сколько единиц транспорта каждого вида
потребуется для перевозки этого оборудования.

16.

Пусть x ‒ количество единиц I-ого вида транспорта,
y ‒ количество единиц II-ого вида транспорта,
z ‒ количество единиц III-его вида транспорта. Тогда
Решим систему уравнений методом Крамера:
Δ=
=12+12+20-3-30-32=-21 ;
Δх =
=380+740+500-185-950-800=-315;
х=
= 15;

17.

Δу =
=1200+570+740-300-1110-1520=-420;
у=
Δz =
= 20;
=555+600+1900-285-1500-1480=-210;
Z=
= 10.
Ответ: Транспорта I-ого вида использовано 15 единиц,
II-ого вида 20 единиц, а III-го вида 10 единиц.

18.

Доклад №3.
Из некоторого листового материала необходимо
выкроить 360 заготовок типа А, 300 заготовок типа
Б и 675 заготовок типа В. При этом можно
применять три способа раскроя. Количество
заготовок, получаемых из каждого листа при
каждом способе раскроя, указано в таблице:
Тип
заготовки
А
Б
В
1
3
1
4
Способ раскроя
2
2
6
1
3
1
2
5
Найти количество листов материала,
раскраиваемых соответственно первым,
вторым и третьим способами.

19.

Обозначим через x, y, z
количество листов материала,
раскраиваемых соответственно
первым, вторым и третьим
способами.
По условию задачи составим
систему уравнений:

20.

Ответ: первым способом раскраивается 90 листов,
вторым – 15, третьим – 60.

21.

ДОКЛАД №4.
Частным лицом куплены три пакета
акций общей стоимостью 485 ден.
ед., причем акции первой группы
куплены по 5 ден. ед. за акцию,
второй – по 20, третьей – по 13.
Через месяц стоимость акций
первой, второй и третьей групп
составила соответственно 6, 14 и 19
ден. ед., а стоимость всего пакета
была 550 ден. ед.
Еще через месяц они стоили по 8, 22
и 20 ден. ед. соответственно, а весь
пакет стоил 660 ден. ед. Cколько
акций каждой группы было
куплено?

22.

Пусть акции I-ой группы было куплено х
штук,
акций II-ой группы y штук,
акций III-ей группы z штук.
Согласно условию задачи имеем:
Решим систему уравнений методом Крамера:
Δ =
=
= 1400+3040+1716-1456-2090-2400=210;

23.

=
= 135800+250800+157300-120120-202730-220000=1050;
=
= 55000+73720+51480-57200-62700-58200=2100;
=
= 46200+88000+64020-54320-60500-79200=4200;
x=
= 5;
y=
= 10;
z=
= 20;
Ответ: Акций I-й группы было куплено 5 штук, акций II-ой
группы
было куплено 10 штук, акций III-ей группы было куплено 20 штук.

24.

Карл Фридрих Гаусс
Карл Фридрих Гаусс родился 30 апреля 1777
г. Гаусс с детства проявлял все признаки
гениальности. Главный труд всей своей
жизни, «Арифметические исследования»,
юноша закончил ещё в 1798 г.
В 1799 г. Гаусс заочно защищает
диссертацию.
Самым знаменитым трудом, проделанным
Карлом Фридрихом Гауссом, была работа
под названием «Теория движения
небесных тел». Именно в ней ученый
предложил теорию возмущения орбит.
Знаменитая теорема алгебры,
термин «гауссова кривизна», основы
дифференциальной геометрии вошли в
основу фундаментальных
математических законов.

25.

Габриэль Крамер
Габриэль Крамер родился 31 июля 1704 года в
Женеве (Швейцария) в семье врача. Уже в
детстве он опережал своих сверстников в
интеллектуальном развитии и
демонстрировал завидные способности в
области математики.
В 18 лет он успешно защитил диссертацию.
Талантливый учёный написал множество
статей на самые разные темы: геометрия,
история, математика, философия. В 1730
году он опубликовал труд по небесной
механике.
Крамер является одним из создателей
линейной алгебры. В работе «Введение в
анализ алгебраических кривых» Крамер
строит систему линейных уравнений и
решает её с помощью алгоритма,
названного позже его именем – метод
Крамера.

26.

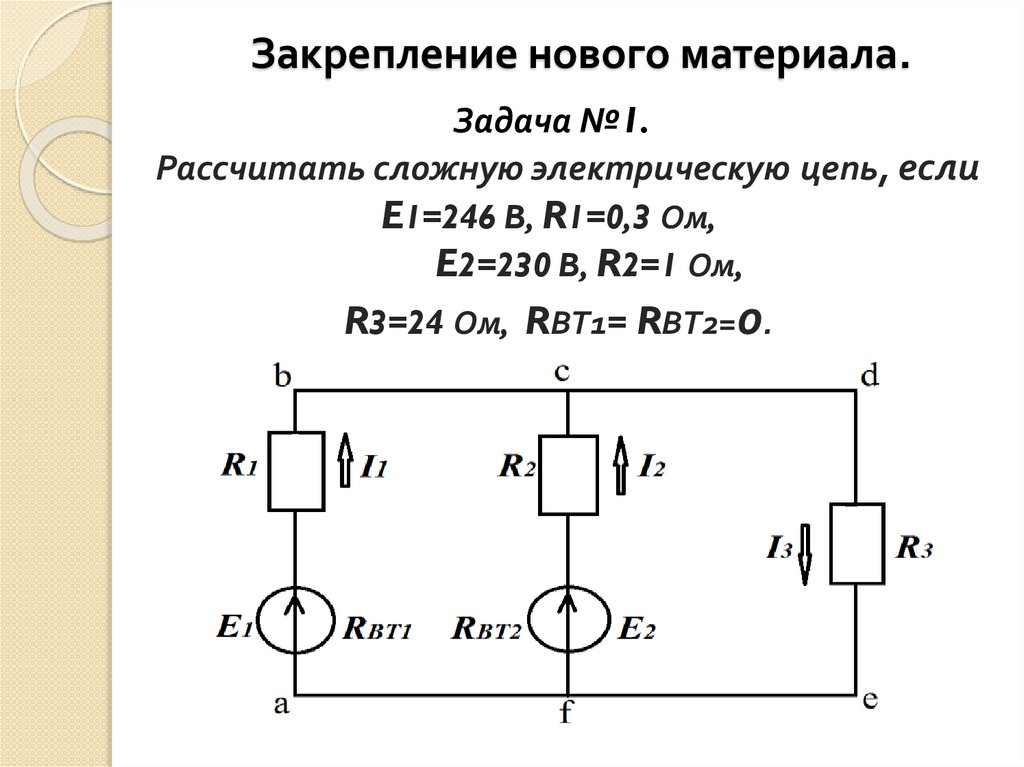
Закрепление нового материала.
Задача №1.
Рассчитать сложную электрическую цепь, если
E1=246 B, R1=0,3 Ом,
E2=230 B, R2=1 Ом,
R3=24 Ом, RВТ1= RВТ2=0.

27.

Задача №2.
Предприятием по производству бытовой
техники в 1 квартале выпущено 4000
вентиляторов, 2000 миксеров и 6000
электрочайников на общую сумму 23 млн
рублей.
Во 2 квартале выпущено 3000 вентиляторов,
1000 миксеров и 4000 электрочайников на
общую сумму 15,6 млн рублей.
В 3 квартале выпущено 1000 вентиляторов,
3000 миксеров и 1000 электрочайников на
общую сумму 7,8 млн рублей.
Найти стоимость одного вентилятора,
одного миксера и одного электрочайника.

28.

Рефлексия
Выберите смайлик, характеризующий ваше
состояние на занятии.

29.

Домашнее задание.
Если ширину производственной
прямоугольной площадки
увеличить на 4 м, а ее длину
уменьшить на 2 м, то ее
площадь увеличится на 32
;
если же ширину уменьшить на
3 м, а длину увеличить на 1 м,
то ее площадь уменьшится на
39
. Найдите длину и
ширину площадки.

30.

Спасибо за
внимание!