Similar presentations:
Вариационные ряды. Средние величины и их оценка
1.
Вариационные ряды.Средние величины и их оценка.
Зимина Е.А.,367 группа
2.
– это ряд числовых измерений определенного признака,
отличающихся друг от друга по величине, расположенных в определенном
порядке. Вариационный ряд состоит из вариант (V) и соответствующих им
частот (Р).
– это каждое числовое значение изучаемого признака.
– это абсолютная численность отдельных вариант в совокупности,
указывающая, сколько раз встречается данная варианта в вариационном ряду.
из которых вариационный ряд состоит,
обозначают буквой n.
- это величина, которая одним числовым значением дает
представление обо всей статистической совокупности (вариационного ряда).
3.
Виды вариационных рядовВариационных ряды могут быть следующих видов:
— дискретный;
— непрерывный .
— несгруппированный;
— сгруппированный (интервальный)
— простой ( р =1);
— взвешенный ( р >1).
4.
• Они применяются для характеристики здоровья населения: рождаемости,заболеваемости, инвалидности, смертности, в описании симптомов и течения различных
болезней, физического развития отдельных контингентов, при обобщении результатов
научных экспериментов.
• При характеристике организации медицинской помощи населению используются такие
понятия, как среднее число врачебных посещений на одного жителя в год, средняя
численность населения на терапевтическом и педиатрическом участке и т.д.
5.
Существуют две группы характеристик вариационного ряда:6.
Наиболее употребительными в статистических исследованияхявляются три вида средних:
1. средняя арифметическая;
2. мода;
3. медиана;
7.
арифметическая(mean) — применяется, если варианты возрастают (убывают) варифметической прогрессии.
1.
Средняя
арифметическая
характеризует
средний
уровень
статистической совокупности.
- для простого ряда, где
∑v – сумма вариант,
n – число наблюдений.
2. Для взвешенного ряда, где
∑vр – сумма произведений
каждой варианты на частоту ее
встречаемости
n – число наблюдений
8.
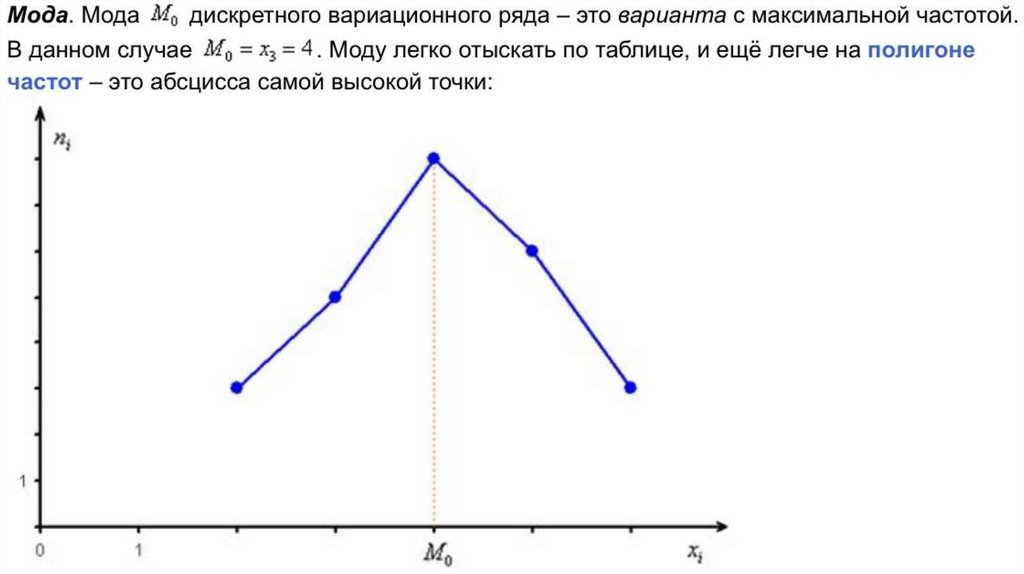
(Мо) (mode)- наиболее часто встречающаяся в вариационном ряду варианта.Практическое значение моды заключается в том, что, не проводя порой достаточно
сложных расчетов, а, ориентируясь на моду, можно знать примерное значение средней
величины.
Мода используется:
• при малом числе наблюдений, когда велико влияние состава
совокупности на среднюю ;
• для характеристики центральной тенденции при ассиметричных
распределениях, когда велико влияние на среднюю крайних
вариант;
9.
10.
МЕДИАНОЙ называется варианта, делящая вариационный ряд пополам.Практическое значение медианы заключается в том, что в симметричном
вариационном ряду, котором в обе стороны от середины находится
равное число вариант, она по своему значению наиболее близка к
средней величине.
При нахождении медианы дискретного вариационного ряда могут возникнуть
два случая:
1) число вариант нечетно (k=2m+1),
2) число вариант четно (k=2m)
В первом случае Me=xm+1, т. е. медиана равна центральной (срединной)
варианте ряда, во втором случае Me,=(xm+xm+1)/2, т.е. медиана принимается
равной полу сумме находящихся в середине ряда вариант








 mathematics
mathematics








