Статистические оценки параметров распределения случайных величин по выборкам. Вариационные ряды и их графики

1.

Тема лекции 4.
Статистические оценки параметров распределения
случайных величин по выборкам. Структурные средние.

2.

Вариационные ряды и их графики дают
наглядное представление о варьировании
признаков, но они недостаточны для полного
описания варьирующих объектов. Для этой
цели
служат
особые,
логически
и
теоретически
обоснованные
числовые
показатели, называемые статистическими
характеристиками.

3.

К числу важнейших показателей, используемых в
статистическом анализе, относят:
1) средние величины;
2) показатели разнообразия и
3) показатели соответствия выборочных данных
параметрам генеральной совокупности.

4.

В зависимости от того, как распределены первичные
данные – в равно- или в неравноинтервальный
вариационный ряд , - для их характеристики
применяют разные средние величины. Именно при
распределении
собранных
данных
в
неравноинтервальный вариационный ряд более
подходящей обобщающей характеристикой изучаемого
объекта
служит
так
называемая
плотность
распределения, т.е. отношение частот или частей к
ширине классовых интервалов. Кроме того, числовыми
характеристиками таких рядов могут служить средние
из абсолютных или относительных показателей
плотности
распределения.
Средняя
плотность
показывает, сколько единиц данной совокупности
приходится в среднем на интервал, равный единице
измерения учитываемого признака.

5.

Средние
величины.
В
отличие
от
индивидуальных числовых характеристик средние
величины обладают большей устойчивостью,
способностью характеризовать целую группу
однородных единиц одним средним числом.
Различают структурные (мода, медиана) и
степенные (средняя арифметическая, средняя
взвешенная и др.) средние.

6.

Показатели
средних
величин
обладают
следующими свойствами:
•являются обобщенными статистическими
параметрами,
они
позволяют
получать
срединное
значение
варьирующего
показателя;
•средняя – это величина абстрактная, т.к. при
ее вычислении можно получать такие
дробные
значения,
которые
в
действительности не могут иметь место в
связи с природой самого признака;
•средняя
величина
имеет
конкретное
выражение, показывая величину признака в
том же наименовании, в котором он
измерялся;

7.

•средние
величины
могут
характеризовать только однородную
совокупность вариант;
•одни средние применяются только в
симметричных рядах (арифметическая,
взвешенная,
квадратичная,
кубическая), другие – в асимметричных
рядах (геометрическая), а третьи – как
в
симметричных,
так
и
в
асимметричных рядах (мода, медиана,
средняя гармоническая).

8.

Структурные средние и способы их
вычисления.
Структурные
величины
представляют собой конкретные варианты
имеющейся совокупности, которые занимают
особое место в ряду распределения.
Мода
(Мо)
–
это
наиболее
часто
встречающаяся варианта в вариационном ряду.
Мода отличается полной независимостью от
крайних значений. Для малых выборок мода не
определяется.

9.

При нормальном распределении величины моды (Mo),
медианы (Ме) и средней арифметической (Х ) равны
. Чем больше асимметрия ряда, тем больше разница
между Мо, Ме, Х
Моду
применяют для характеристики не только
количественных, но и качественных признаков, что важно при
изучении
генетических
особенностей
альтернативных
признаков.

10.

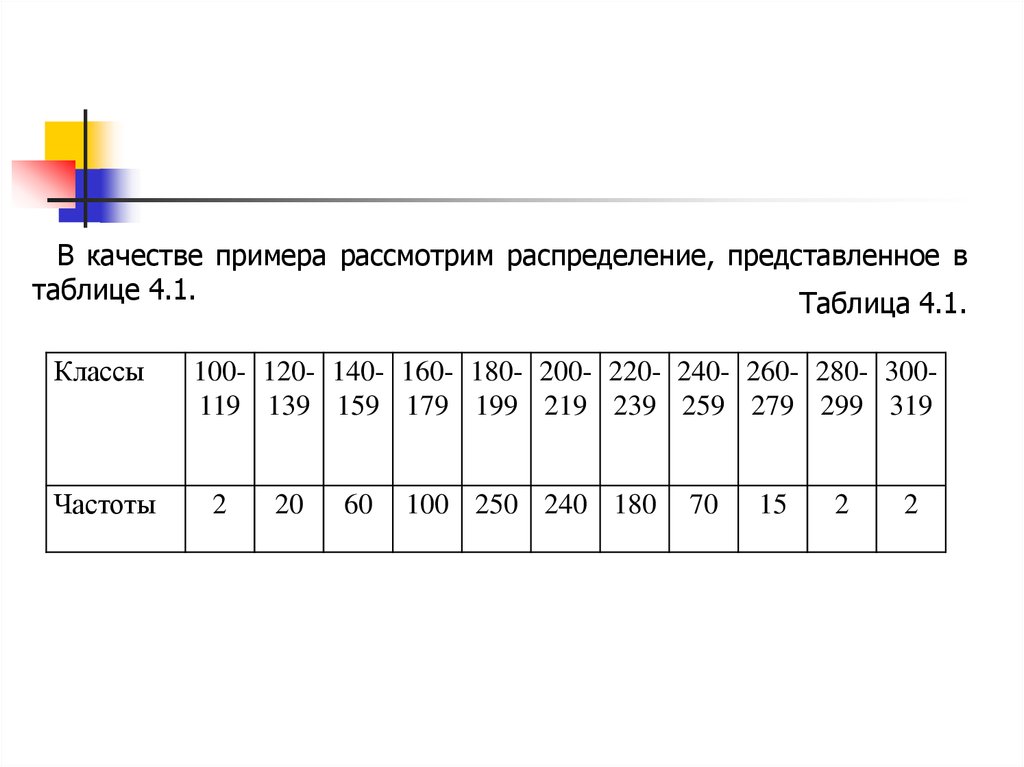
В качестве примера рассмотрим распределение, представленное в
таблице 4.1.
Таблица 4.1.
Классы
Частоты
100- 120- 140- 160- 180- 200- 220- 240- 260- 280- 300119 139 159 179 199 219 239 259 279 299 319
2
20
60
100 250 240 180
70
15
2
2

11.

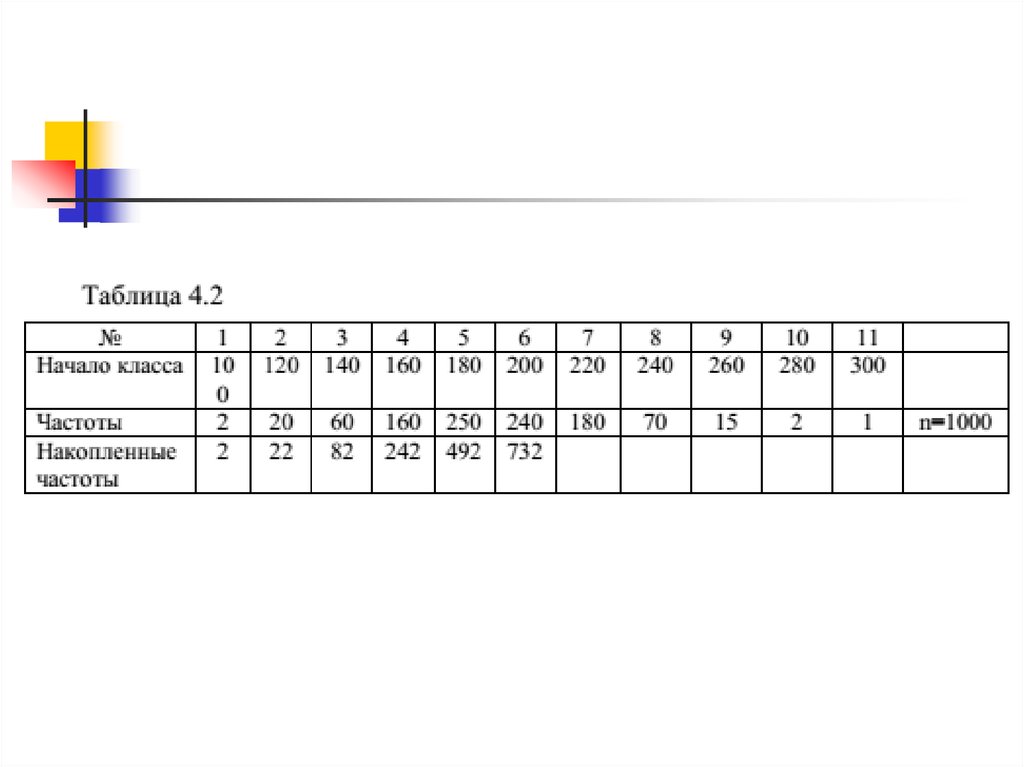
В этом распределении наиболее многочисленным является
пятый класс (180-199 с частотой 250. Это модальный класс.
Формула для вычисления моды (Мо):
Мо = ХМо + k
f 2 f1
(2 f 2 f 1 f 3 )
[2],
где:
ХМо – варианта, соответствующая началу модального класса;
k – классный промежуток;
f1 – частота, предшествующая модальному классу;
f2 – частота модального класса;
f3 – частота, следующая за модальным классом.