Similar presentations:
Пример расчета. Определение усилий в стержнях фермы методом сквозных сечений
1.
ПРИМЕР РАСЧЕТАОПРЕДЕЛЕНИЕ УСИЛИЙ В
СТЕРЖНЯХ ФЕРМЫ МЕТОДОМ
F1=2кН G
E
6
СКВОЗНЫХ СЕЧЕНИЙ
2
XA (-2) A
1
a
YA (1)
5
3
C
4
a
9
7
D
8
a
B
a
F2=5кН YB (4)
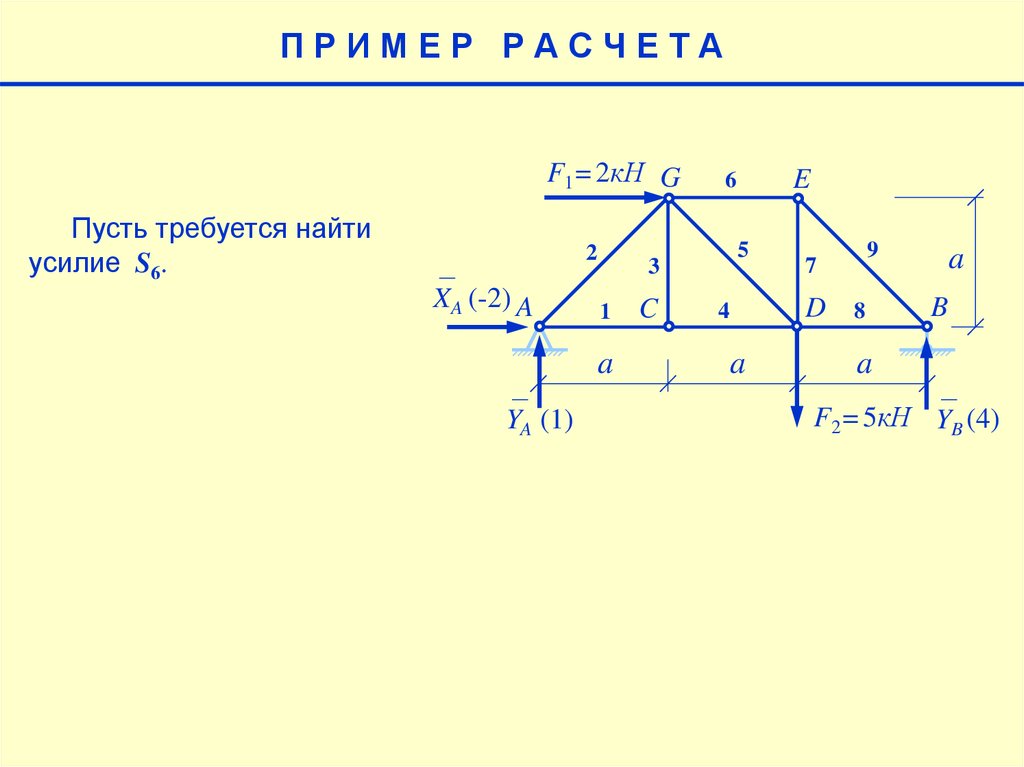
2.
ПРИМЕР РАСЧЕТАF1=2кН G
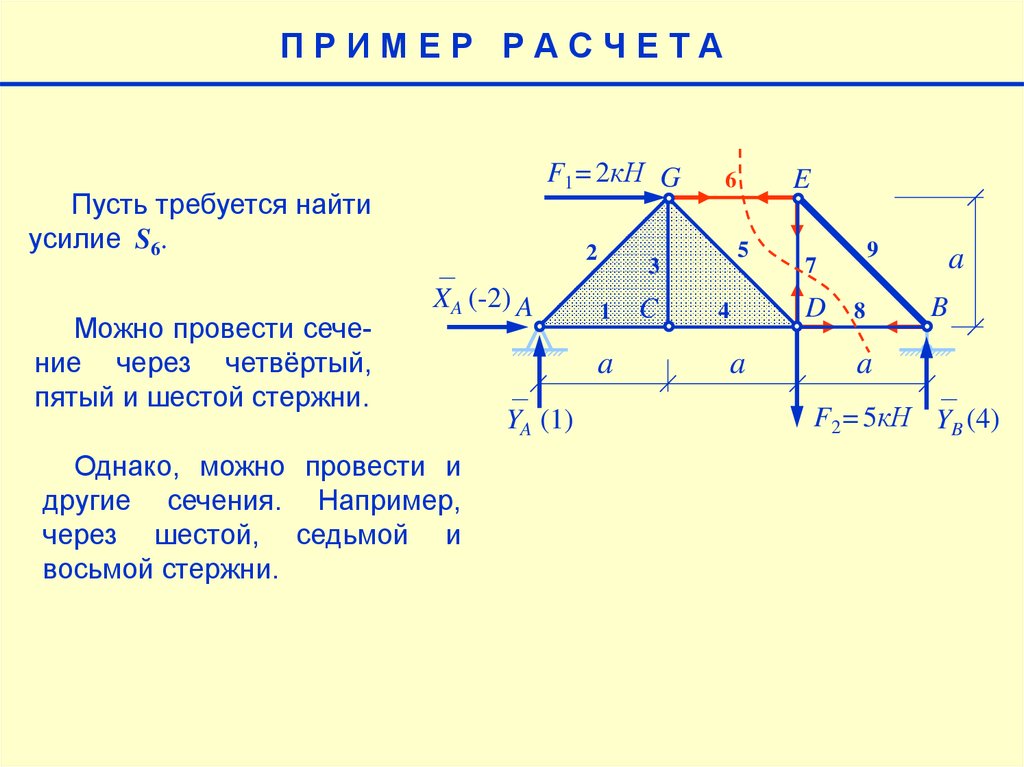
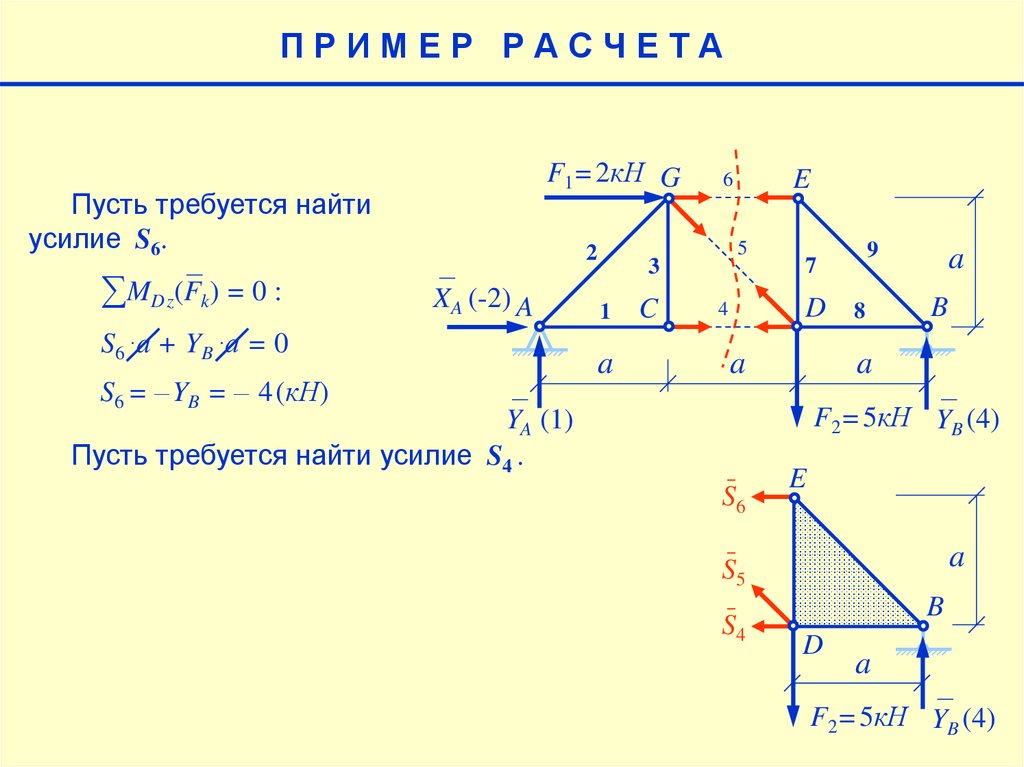
Пусть требуется найти
усилие S6.
2
XA (-2) A
a
YA (1)
5
3
1
C
E
6
4
a
9
7
D
8
a
B
a
F2=5кН YB (4)
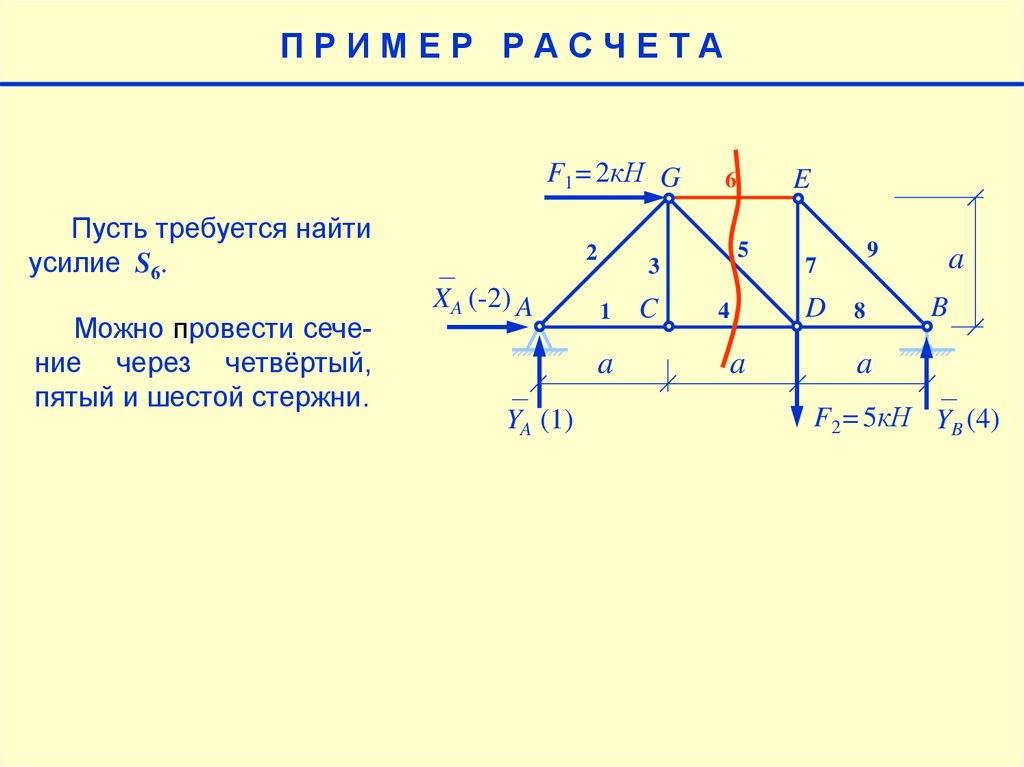
3.
ПРИМЕР РАСЧЕТАF1=2кН G
Пусть требуется найти
усилие S6.
Можно провести сечение через четвёртый,
пятый и шестой стержни.
2
XA (-2) A
a
YA (1)
5
3
1
C
E
6
4
a
9
7
D
8
a
B
a
F2=5кН YB (4)
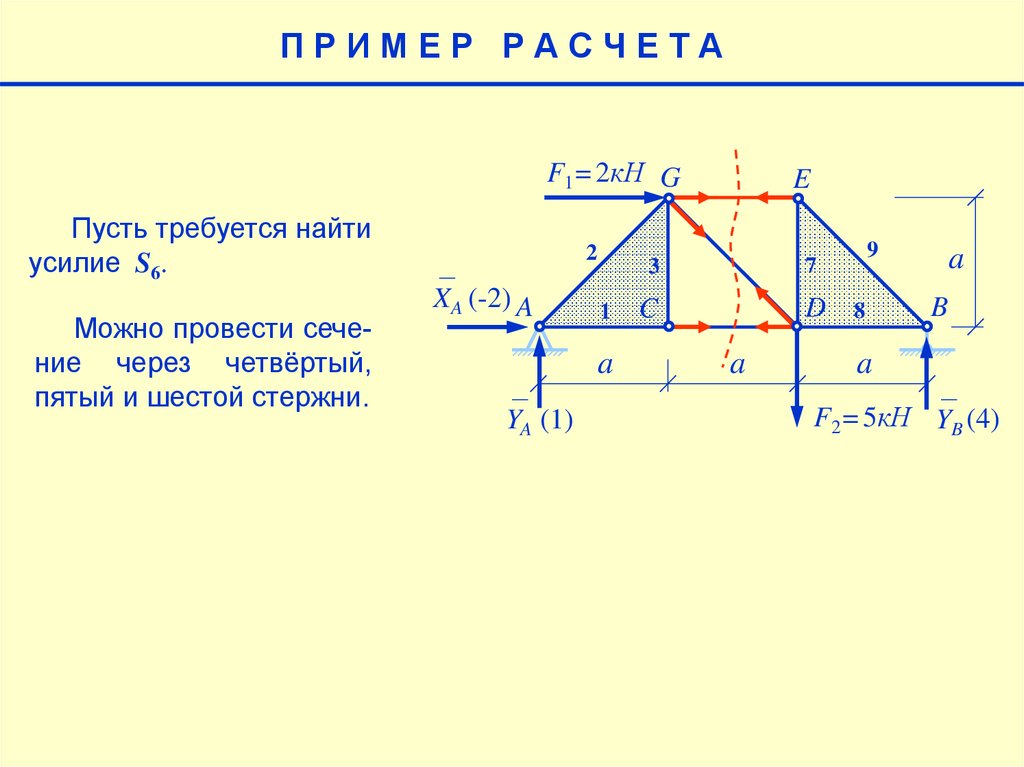
4.
ПРИМЕР РАСЧЕТАF1=2кН G
Пусть требуется найти
усилие S6.
Можно провести сечение через четвёртый,
пятый и шестой стержни.
2
XA (-2) A
1
a
YA (1)
E
3
7
C
D
a
9
8
a
B
a
F2=5кН YB (4)
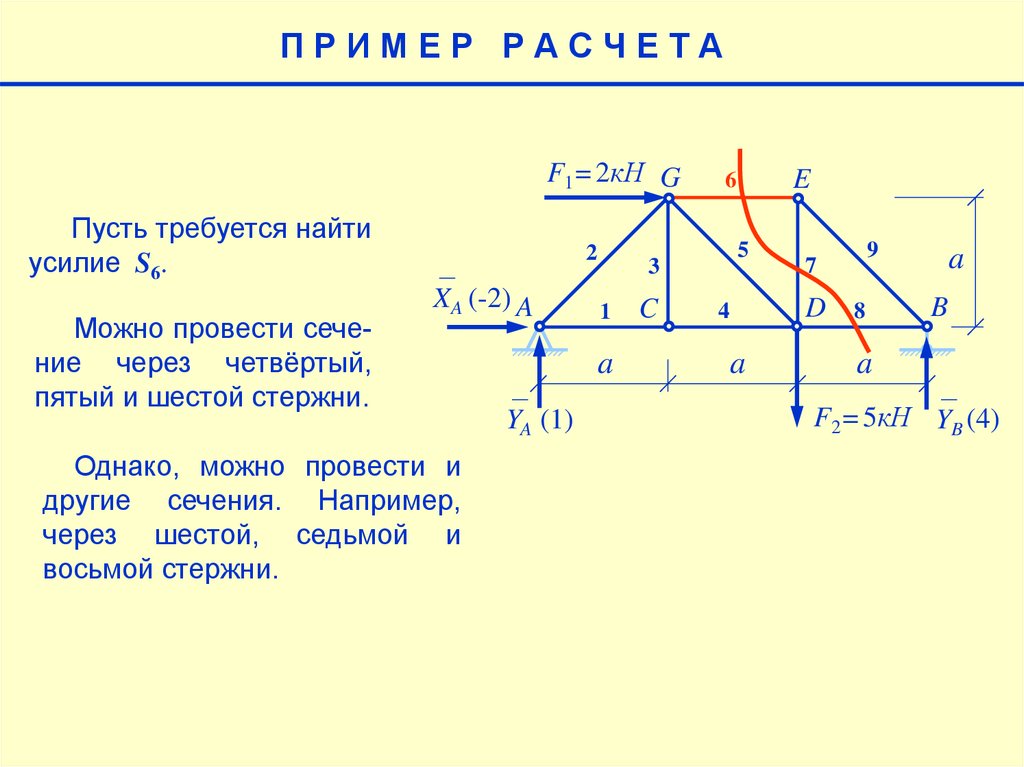
5.
ПРИМЕР РАСЧЕТАF1=2кН G
Пусть требуется найти
усилие S6.
Можно провести сечение через четвёртый,
пятый и шестой стержни.
2
XA (-2) A
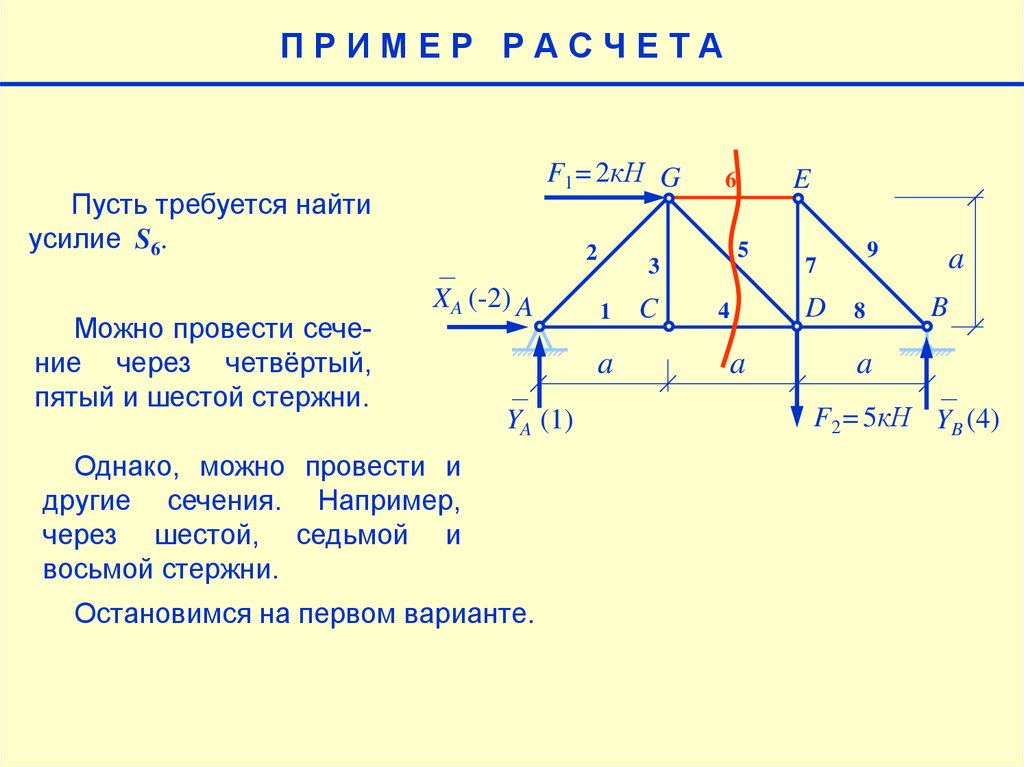
Однако, можно провести и
другие сечения. Например,
через шестой, седьмой и
восьмой стержни.
a
YA (1)
5
3
1
C
E
6
4
a
9
7
D
8
a
B
a
F2=5кН YB (4)
6.
ПРИМЕР РАСЧЕТАF1=2кН G
Пусть требуется найти
усилие S6.
Можно провести сечение через четвёртый,
пятый и шестой стержни.
2
XA (-2) A
Однако, можно провести и
другие сечения. Например,
через шестой, седьмой и
восьмой стержни.
a
YA (1)
5
3
1
C
E
6
4
a
9
7
D
8
a
B
a
F2=5кН YB (4)
7.
ПРИМЕР РАСЧЕТАF1=2кН G
Пусть требуется найти
усилие S6.
Можно провести сечение через четвёртый,
пятый и шестой стержни.
2
XA (-2) A
a
YA (1)
Однако, можно провести и
другие сечения. Например,
через шестой, седьмой и
восьмой стержни.
Остановимся на первом варианте.
5
3
1
C
E
6
4
a
9
7
D
8
a
B
a
F2=5кН YB (4)
8.
ПРИМЕР РАСЧЕТАF1=2кН G
Пусть требуется найти
усилие S6.
Можно провести сечение через четвёртый,
пятый и шестой стержни.
2
XA (-2) A
5
3
1
a
C
E
6
D
4
a
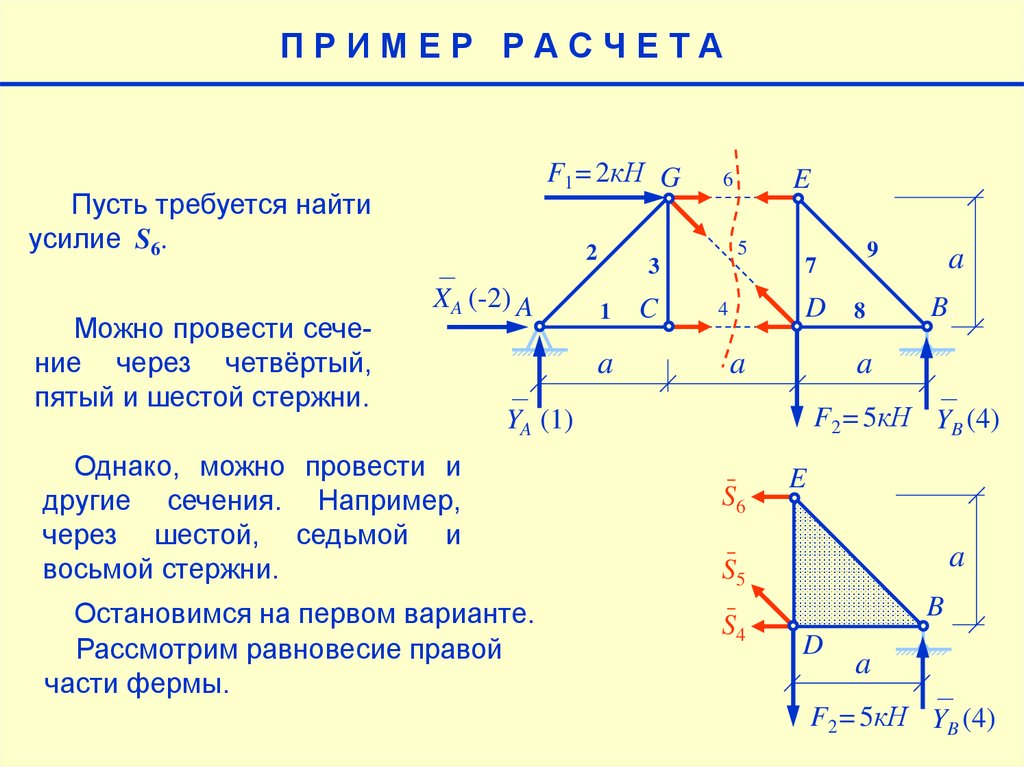
Остановимся на первом варианте.
Рассмотрим равновесие правой
части фермы.
8
a
B
a
F2=5кН YB (4)
YA (1)
Однако, можно провести и
другие сечения. Например,
через шестой, седьмой и
восьмой стержни.
9
7
S6
E
a
S5
S4
B
D
a
F2=5кН YB (4)
9.
ПРИМЕР РАСЧЕТАF1=2кН G
Пусть требуется найти
усилие S6.
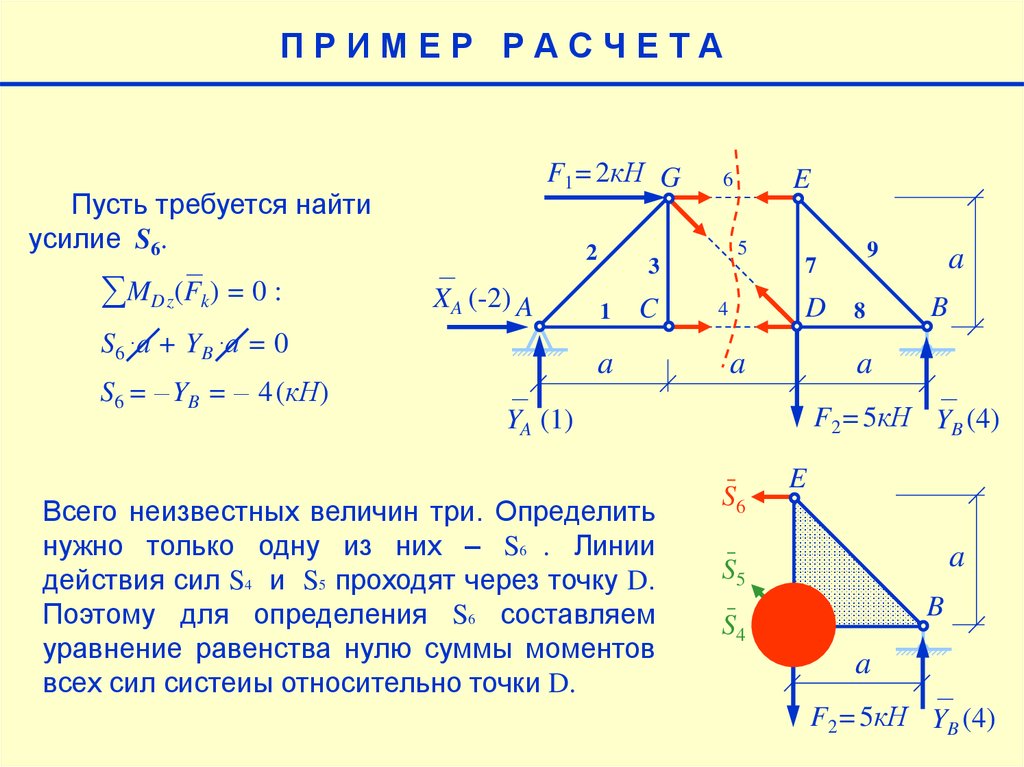
∑ MDz(Fk) = 0 :
2
XA (-2) A
S6 ∙a + YB ∙a = 0
S6 = –YB = – 4(кН)
5
3
1
C
a
E
6
D
4
a
8
a
B
a
F2=5кН YB (4)
YA (1)
Всего неизвестных величин три. Определить
нужно только одну из них – S6 . Линии
действия сил S4 и S5 проходят через точку D.
Поэтому для определения S6 составляем
уравнение равенства нулю суммы моментов
всех сил систеиы относительно точки D.
9
7
S6
E
a
S5
S4
B
D
a
F2=5кН YB (4)
10.
ПРИМЕР РАСЧЕТАF1=2кН G
Пусть требуется найти
усилие S6.
∑ MDz(Fk) = 0 :
2
XA (-2) A
S6 ∙a + YB ∙a = 0
S6 = –YB = – 4(кН)
5
3
1
a
C
E
6
D
4
9
7
a
8
a
B
a
F2=5кН YB (4)
YA (1)
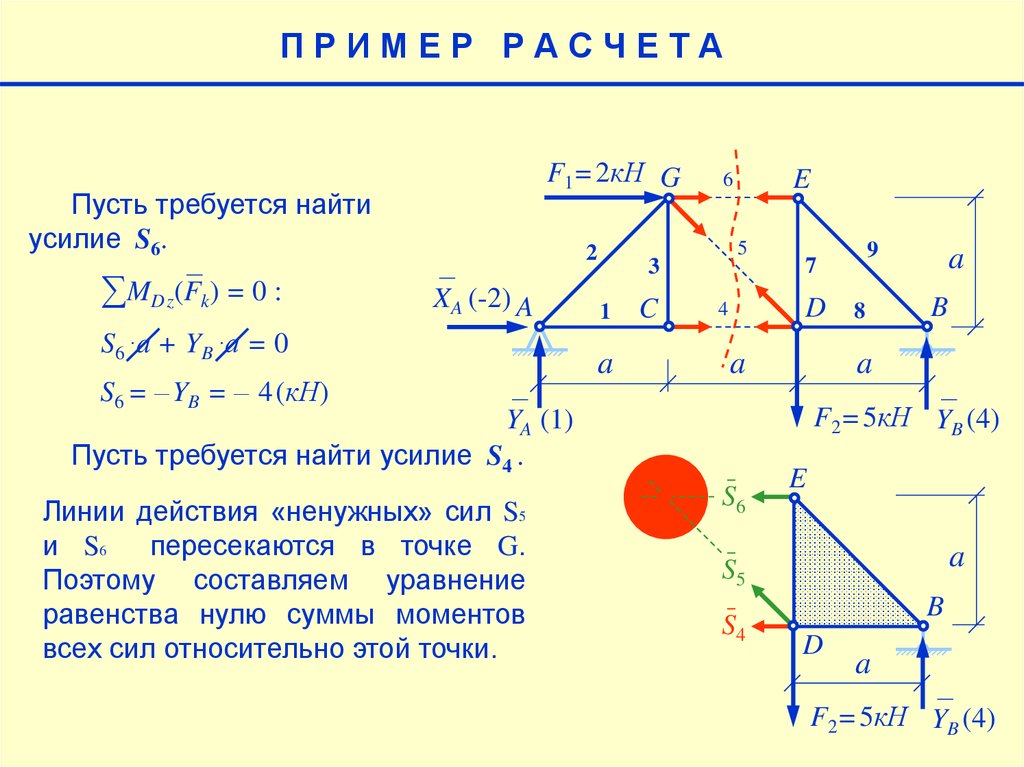
Пусть требуется найти усилие S4 .
S6
E
a
S5
S4
B
D
a
F2=5кН YB (4)
11.
ПРИМЕР РАСЧЕТАF1=2кН G
Пусть требуется найти
усилие S6.
∑ MDz(Fk) = 0 :
2
XA (-2) A
S6 ∙a + YB ∙a = 0
S6 = –YB = – 4(кН)
5
3
1
a
C
E
6
D
4
a
8
a
B
a
F2=5кН YB (4)
YA (1)
Пусть требуется найти усилие S4 .
Линии действия «ненужных» сил S5
и S6
пересекаются в точке G.
Поэтому составляем уравнение
равенства нулю суммы моментов
всех сил относительно этой точки.
9
7
S6
E
a
S5
S4
B
D
a
F2=5кН YB (4)
12.
ПРИМЕР РАСЧЕТАF1=2кН G
Пусть требуется найти
усилие S6.
∑ MDz(Fk) = 0 :
2
XA (-2) A
S6 ∙a + YB ∙a = 0
S6 = –YB = – 4(кН)
YA (1)
Пусть требуется найти усилие S4 .
∑ MGz(Fk) = 0 :
– S4 ∙a – F2 ∙a + YB ∙2a = 0
S4 = – F2 + 2YB = – 5 + 2∙4 = 3(кН)
5
3
1
C
E
6
D
4
a
9
7
a
8
a
B
a
F2=5кН YB (4)
G
S6
E
a
S5
S4
a
B
D
a
F2=5кН YB (4)
13.
ПРИМЕР РАСЧЕТАПусть требуется найти усилие S5 .
F1=2кН G
Как видно, нет точки
пересечения линий действия сил S4 и S6 .
2
Но эти силы имеют XA (-2) A
нулевую проекцию на вертикальную ось
Поэтому
составляем
уравнение равенства нулю
суммы проекций всех сил
на вертикальную ось Dy.
5
3
1
C
E
6
4
a
D
8
у
a
a
a
B
F2=5кН YB (4)
YA (1)
∑ Fky= 0: S5 sin 450 – F2 + YB = 0 => S5 = √2 (кН).
9
7
G
S6
E
a
S5
S4
a
B
D
a
F2=5кН YB (4)



 mathematics
mathematics








