Similar presentations:
Расчет ферм
1.
РАСЧЁТ ФЕРМДокладчик
Егерева Эльвира Николаевна
к.ф.-м.н., доцент кафедры Строительной и Теоретической механики
2.
РАСЧЁТ ФЕРМОпр.1 Фермой называется геометрически
неизменяемая конструкция, состоящая из
стержней.
Опр.2 Места соединений стержней называются
узлами. Если оси всех стержней и вся
приложенная к ферме нагрузка расположены в
одной плоскости, ферма называется плоской.
В дальнейшем будем рассматривать только
плоские фермы.
3.
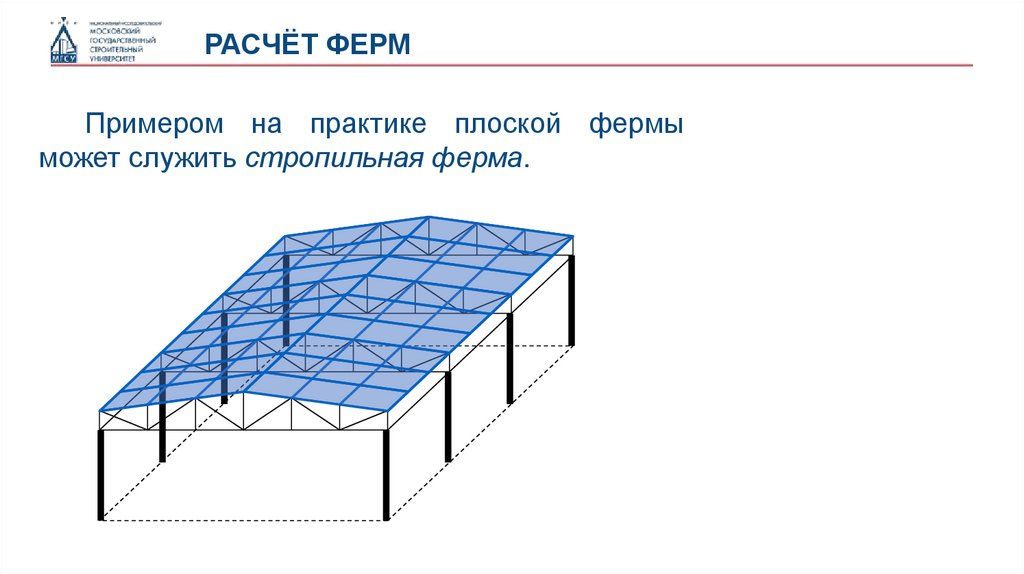
РАСЧЁТ ФЕРМПримером на практике плоской фермы
может служить стропильная ферма.
4.
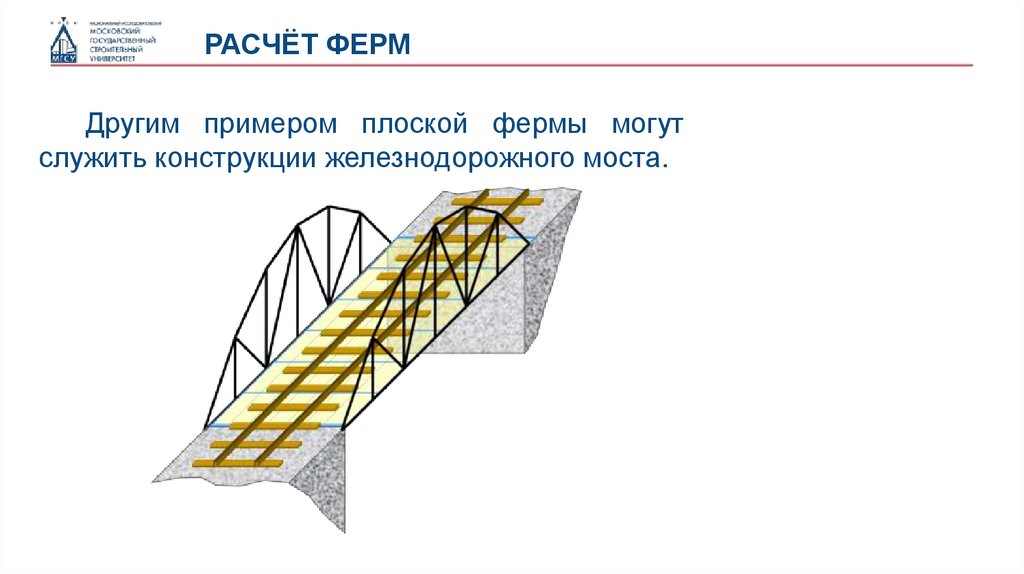
РАСЧЁТ ФЕРМДругим примером плоской фермы могут
служить конструкции железнодорожного моста.
5.
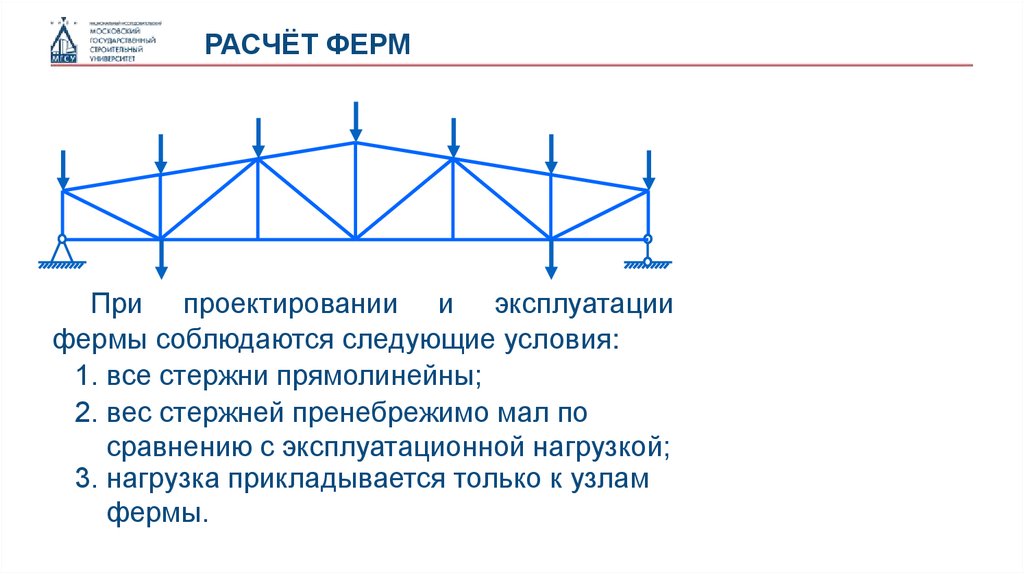
РАСЧЁТ ФЕРМПри проектировании и эксплуатации
фермы соблюдаются следующие условия:
1. все стержни прямолинейны;
2. вес стержней пренебрежимо мал по
сравнению с эксплуатационной нагрузкой;
3. нагрузка прикладывается только к узлам
фермы.
6.
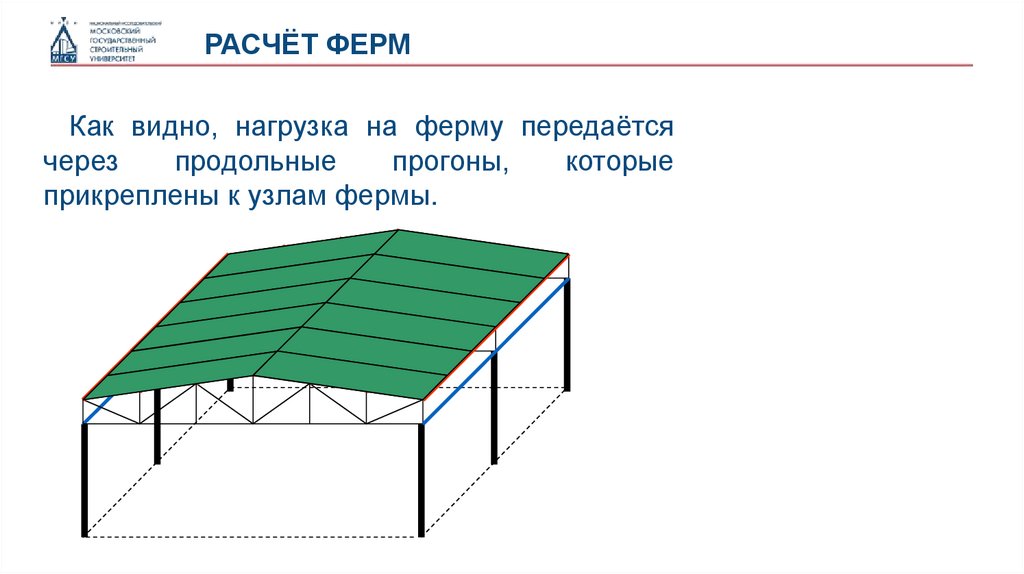
РАСЧЁТ ФЕРМКак видно, нагрузка на ферму передаётся
через
продольные
прогоны,
которые
прикреплены к узлам фермы.
7.
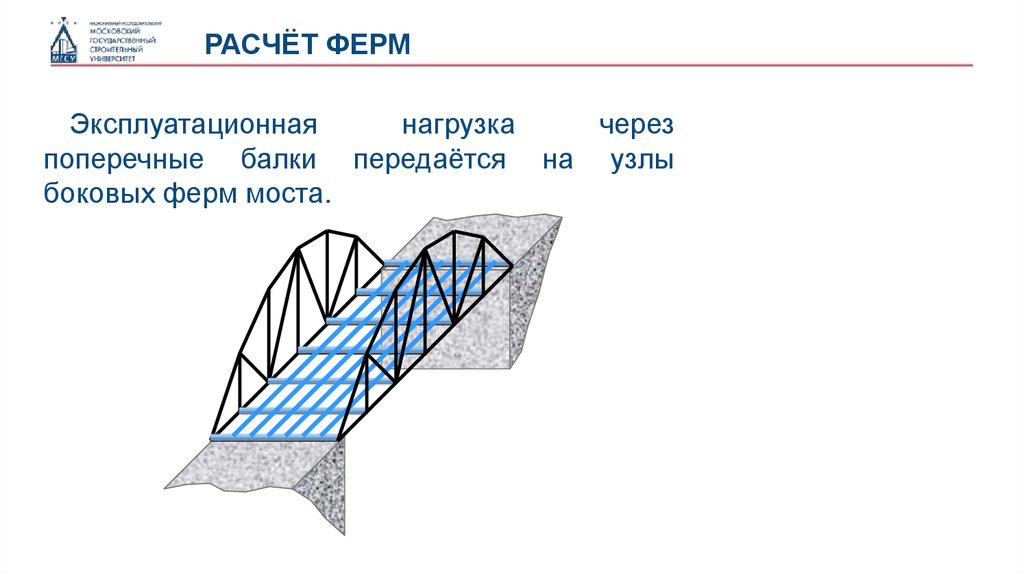
РАСЧЁТ ФЕРМЭксплуатационная
нагрузка
через
поперечные балки передаётся на узлы
боковых ферм моста.
8.
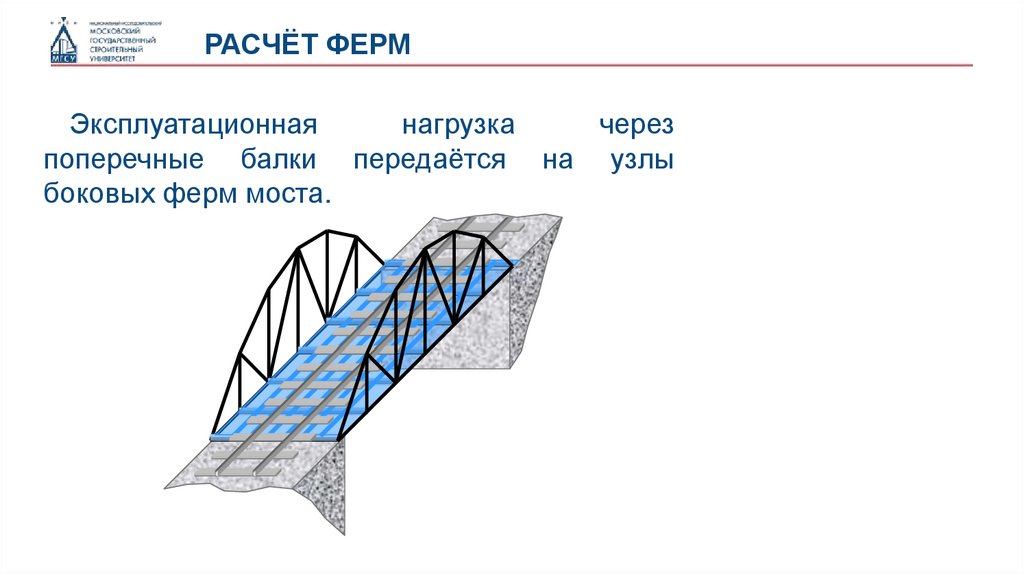
РАСЧЁТ ФЕРМЭксплуатационная
нагрузка
через
поперечные балки передаётся на узлы
боковых ферм моста.
9.
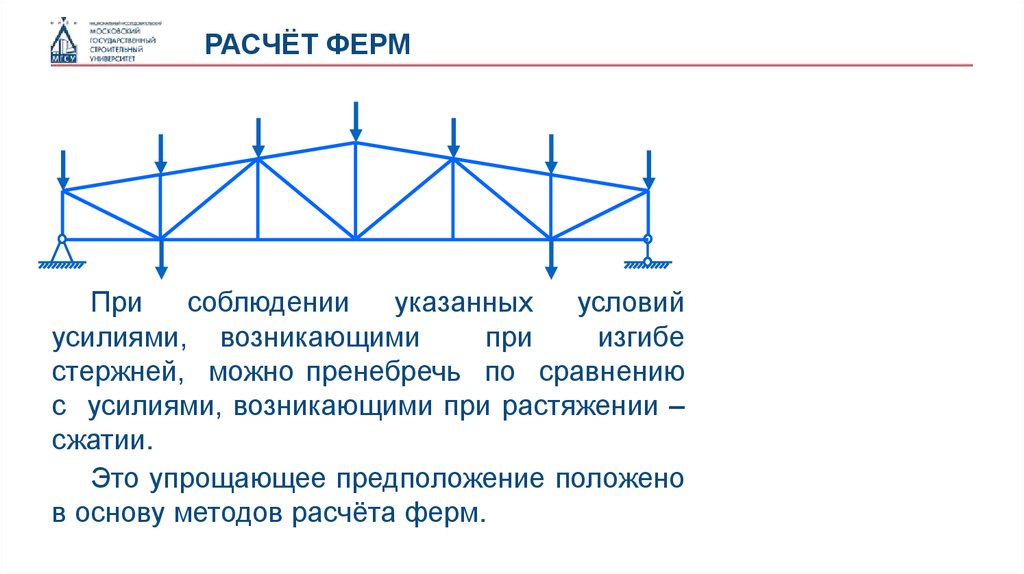
РАСЧЁТ ФЕРМПри
соблюдении
указанных
условий
усилиями, возникающими
при
изгибе
стержней, можно пренебречь по сравнению
с усилиями, возникающими при растяжении –
сжатии.
Это упрощающее предположение положено
в основу методов расчёта ферм.
10.
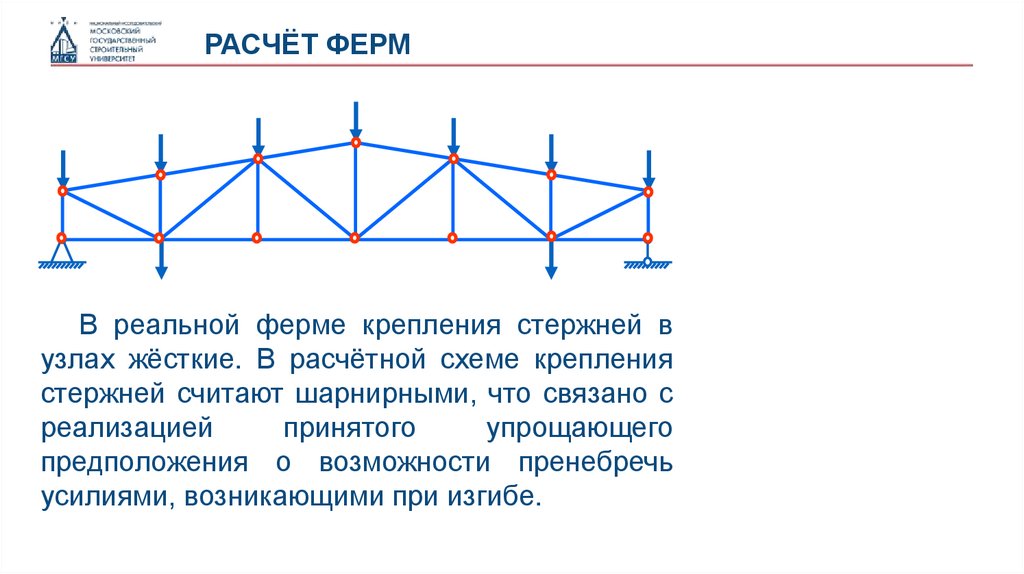
РАСЧЁТ ФЕРМВ реальной ферме крепления стержней в
узлах жёсткие. В расчётной схеме крепления
стержней считают шарнирными, что связано с
реализацией
принятого
упрощающего
предположения о возможности пренебречь
усилиями, возникающими при изгибе.
11.
РАСЧЁТ ФЕРМПри соблюдении оговорённых упрощающих
условий
каждый
стержень
фермы
оказывается
нагруженным
силами,
приложенными на концах стержня.
12.
РАСЧЁТ ФЕРМПри соблюдении оговорённых упрощающих
условий
каждый
стержень
фермы
оказывается
нагруженным
силами,
приложенными на концах стержня.
Силы, приложенные в одной точке можно
заменить равнодействующей.
13.
РАСЧЁТ ФЕРМУсилие
в
стержне
считается
положительным, если он растянут
и отрицательным, если стержень сжат.
В результате расчёта фермы необходимо
определить реакции опор и найти усилия во
всех стержнях фермы.
Методы расчёта ферм рассмотрим на
примере.
или
14.
РАСЧЁТ ФЕРМF1=2кН
a
a
a
a
F2=5кН
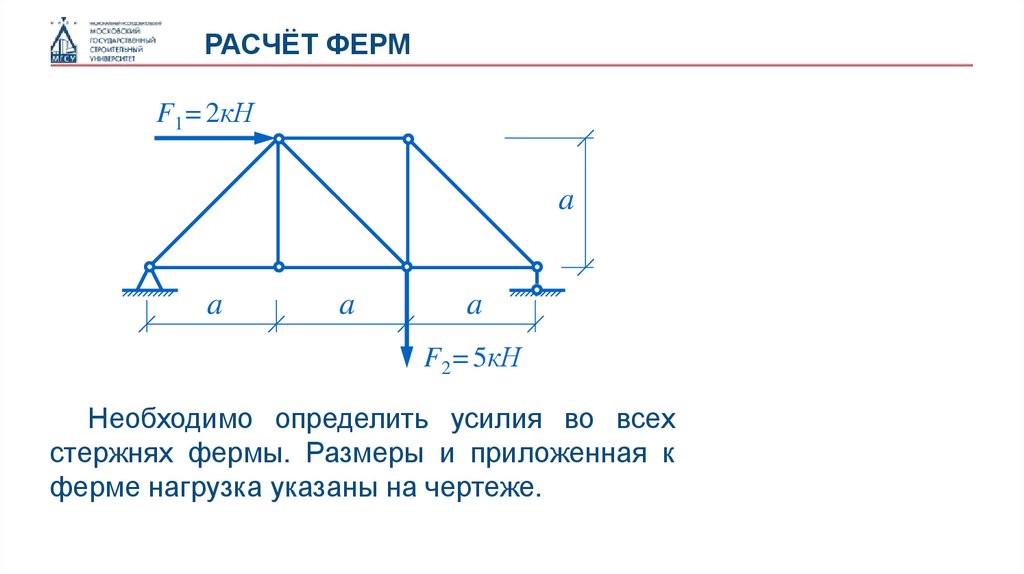
Необходимо определить усилия во всех
стержнях фермы. Размеры и приложенная к
ферме нагрузка указаны на чертеже.
15.
РАСЧЁТ ФЕРМF1=2кН G
2
A
5
3
1
a
C
E
6
4
a
9
7
D
8
a
B
a
F2=5кН
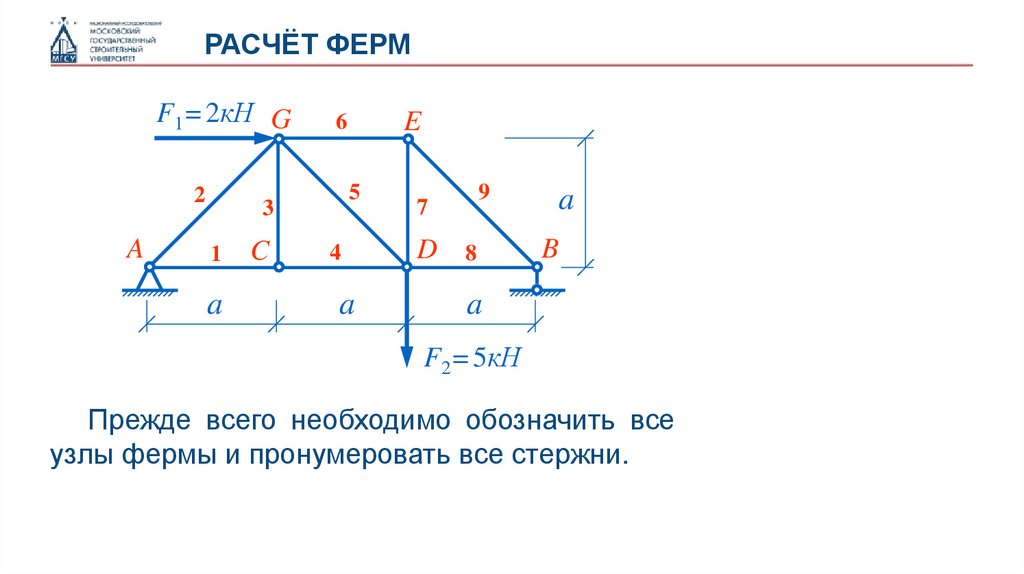
Прежде всего необходимо обозначить все
узлы фермы и пронумеровать все стержни.
16.
РАСЧЁТ ФЕРМF1=2кН G
2
A
5
3
1
a
C
E
6
4
a
9
7
D
8
a
B
a
F2=5кН
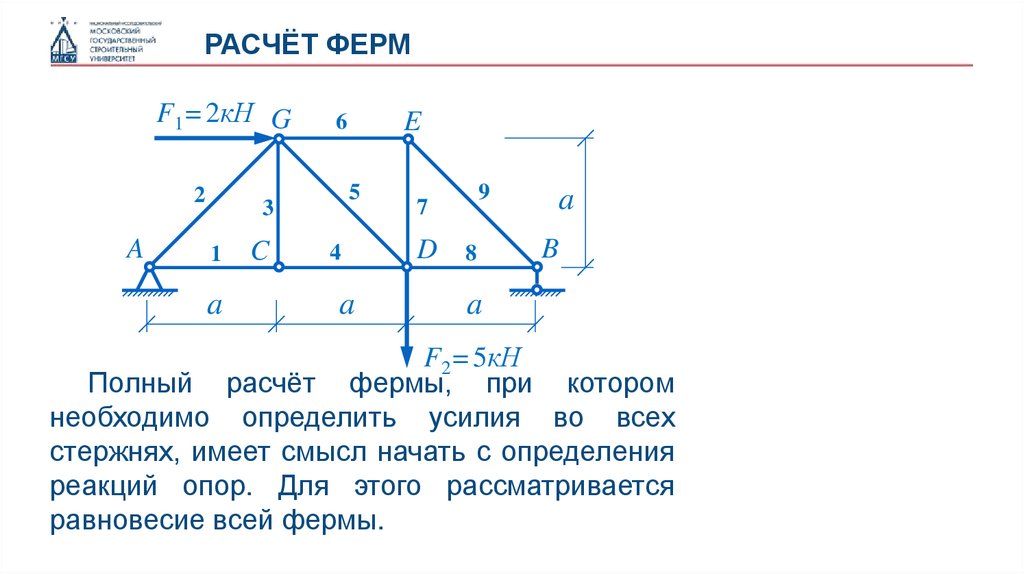
Полный расчёт фермы, при котором
необходимо определить усилия во всех
стержнях, имеет смысл начать с определения
реакций опор. Для этого рассматривается
равновесие всей фермы.
17.
РАСЧЁТ ФЕРМF1=2кН G
2
A
5
3
1
a
C
E
6
4
a
9
7
D
8
a
B
a
F2=5кН
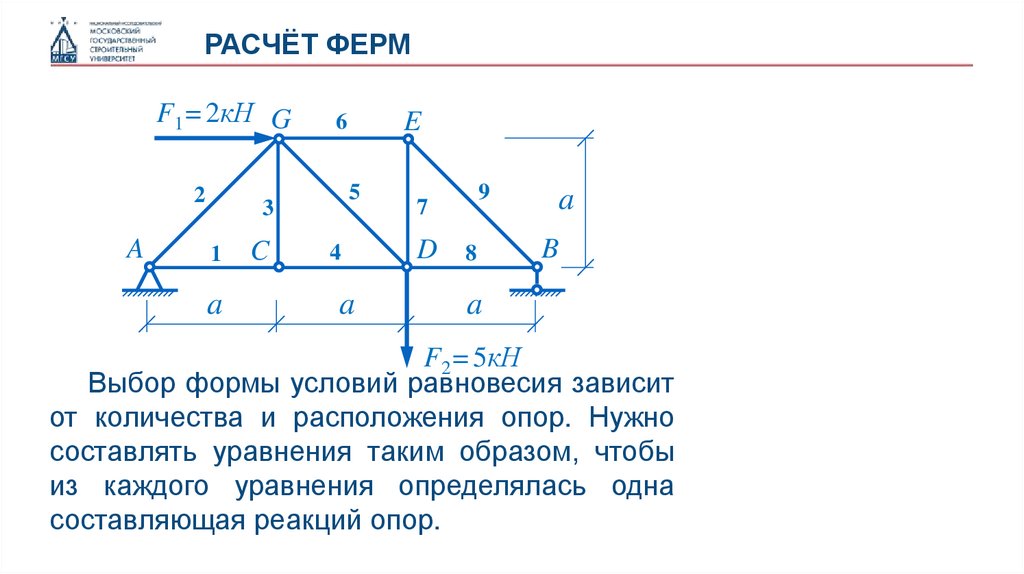
Выбор формы условий равновесия зависит
от количества и расположения опор. Нужно
составлять уравнения таким образом, чтобы
из каждого уравнения определялась одна
составляющая реакций опор.
18.
РАСЧЁТ ФЕРМF1=2кН G
2
RAX (-2)A
5
3
1
a
C
E
6
4
a
9
7
D
8
a
B
a
RAY (1)
F2=5кН RBY (4)
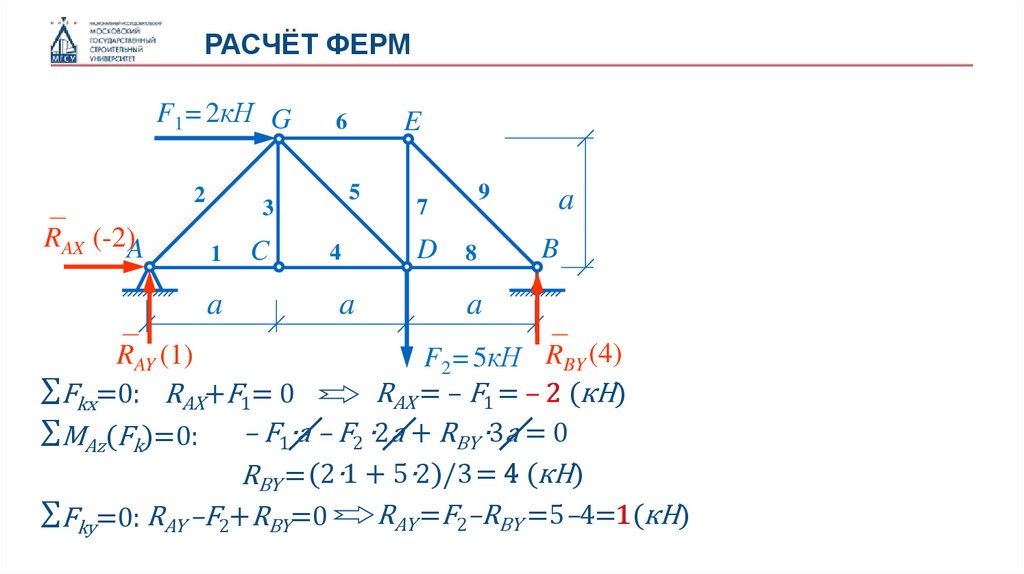
∑Fkx=0: RAX+F1= 0
RAX = – F1 = – 2 (кН)
∑MAz(Fk)=0:
– F1∙a – F2 ∙2a + RBY ∙3a = 0
RBY = (2∙1 + 5∙2)/3 = 4 (кН)
∑Fky=0: RAY –F2+RBY=0
RAY =F2–RBY =5–4=1(
1 кН)
19.
РАСЧЁТ ФЕРМF1=2кН G
2
RAX (-2)A
5
3
1
a
C
E
6
4
a
9
7
D
8
a
B
a
RAY (1)
F2=5кН RBY (4)
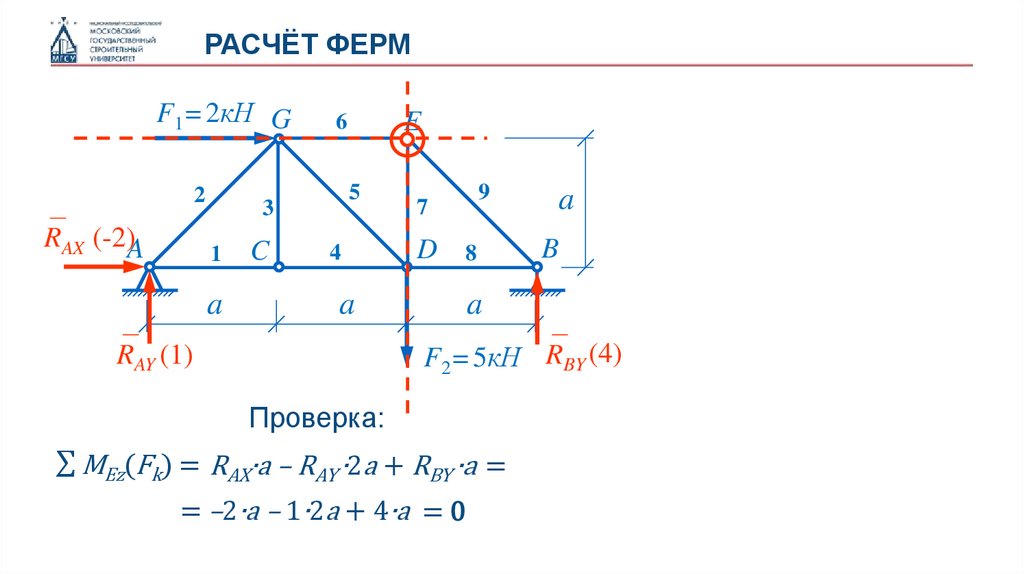
Для проверки правильности полученных
результатов составим уравнение моментов
относительно такой точки, относительно
которой все вычисленные силы реакций
создают ненулевые моменты.
20.
РАСЧЁТ ФЕРМF1=2кН G
2
RAX (-2)A
5
3
1
a
C
E
6
4
9
7
D
8
a
a
B
a
F2=5кН RBY (4)
RAY (1)
Проверка:
∑ MЕz(Fk) = RAX∙a – RAY ∙2a + RBY ∙a =
= –2∙a – 1∙2a + 4∙a = 0
21.
РАСЧЁТ ФЕРМF1=2кН G
2
RAX (-2)A
a
RAY (1)
5
3
1
C
E
6
4
a
9
7
D
8
a
B
a
F2=5кН RBY (4)
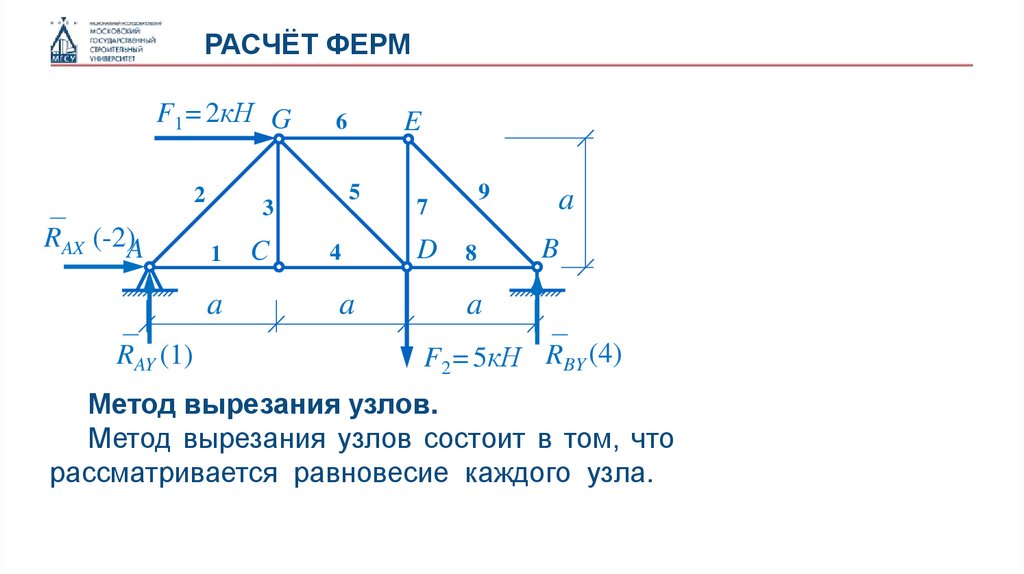
Метод вырезания узлов.
Метод вырезания узлов состоит в том, что
рассматривается равновесие каждого узла.
22.
РАСЧЁТ ФЕРМF1=2кН G
2
RAX (-2)A
5
3
1
a
C
E
6
4
a
9
7
D
8
a
B
a
RAY (1)
F2=5кН RBY (4)
На каждый узел действует плоская система
сходящихся сил, состоящая из приложенных к
данному узлу активных сил и реакций
стержней, присоединённых к данному узлу.
23.
РАСЧЁТ ФЕРМF1
S2
G
S6
S5
S3
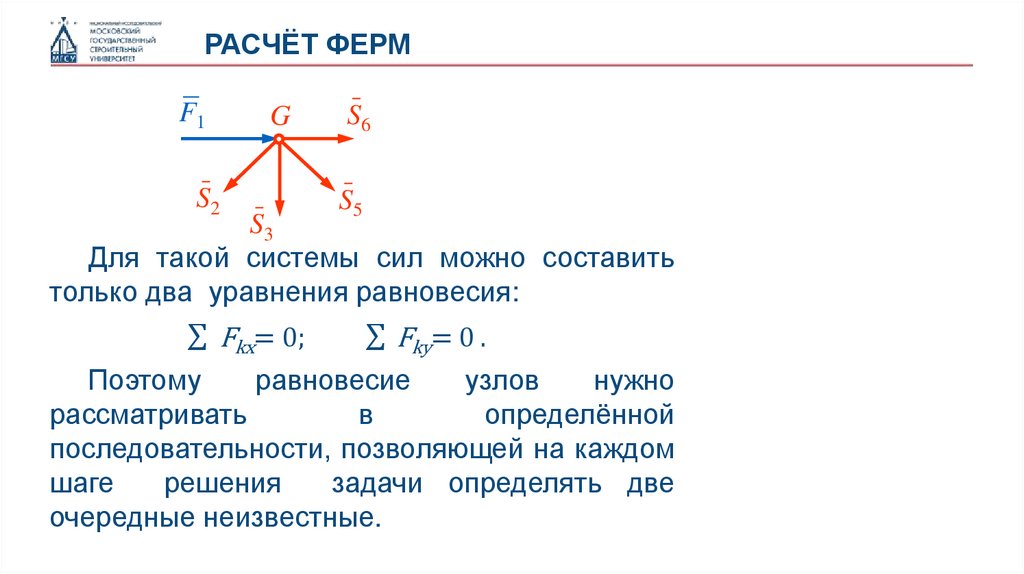
Для такой системы сил можно составить
только два уравнения равновесия:
∑ Fkx= 0;
∑ Fky= 0 .
Поэтому
равновесие
узлов
нужно
рассматривать
в
определённой
последовательности, позволяющей на каждом
шаге
решения
задачи определять две
очередные неизвестные.
24.
РАСЧЁТ ФЕРМF1=2кН G
2
RAX (-2)A
a
RAY (1)
5
3
1
C
E
6
D
4
a
9
7
8
a
B
a
F2=5кН RBY (4)
25.
РАСЧЁТ ФЕРМПравило знаков:
«+» – растягивающие усилия
(направлены от узла);
«–» – сжимающие усилия.
Изначально при расчете все усилия
предполагаются
положительными
и
направляются от узлов.
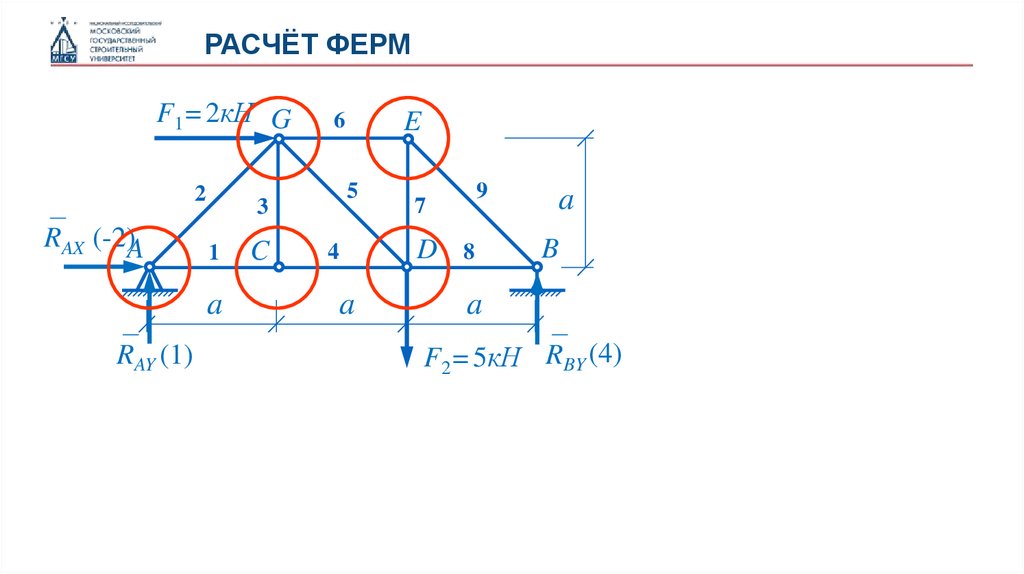
26.
РАСЧЁТ ФЕРМF1=2кН G
2
RAX (-2)A
5
3
1
a
C
E
6
D
4
a
9
7
8
a
B
a
F2=5кН RBY (4)
RAY (1)
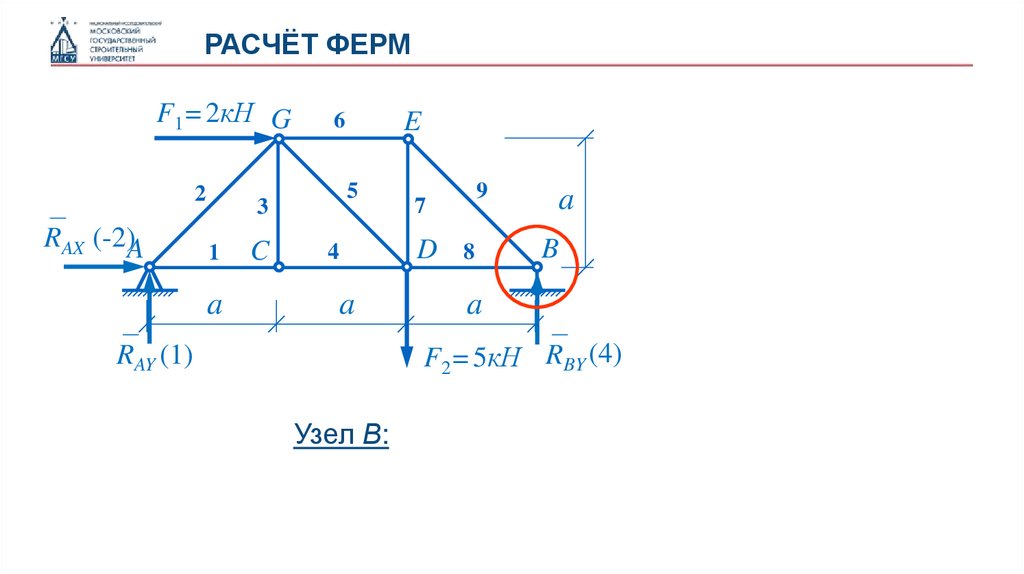
Узел В:
27.
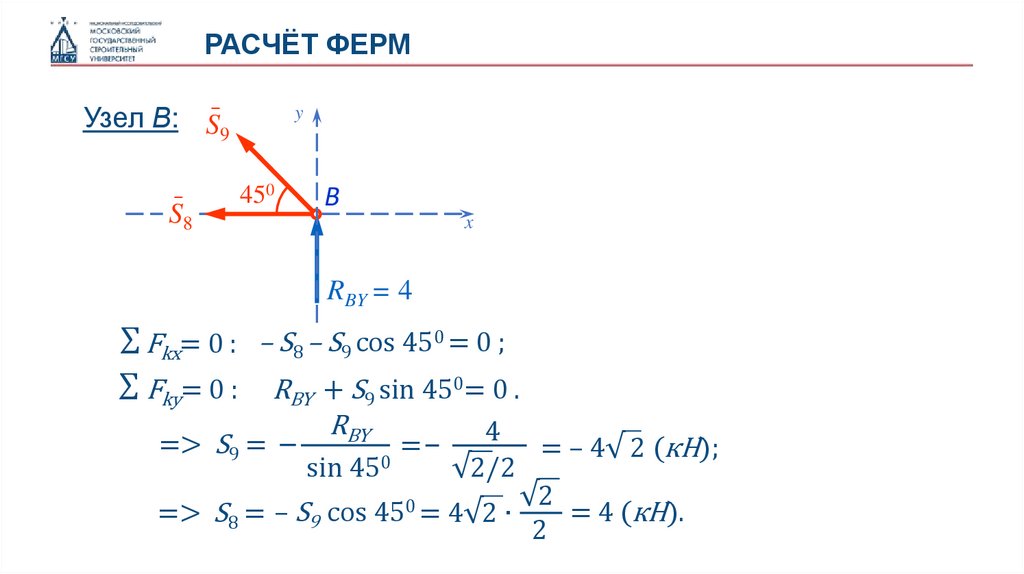
РАСЧЁТ ФЕРМУзел В: S9
S8
y
450
B
x
RBY = 4
∑ Fkx= 0 : – S8 – S9 cos 450 = 0 ;
∑ Fky= 0 : RBY + S9 sin 450= 0 .
RBY
4
= – 4√ 2 (кН);
√2/2
√2
= 4 (кН).
=> S8 = – S9 cos 450 = 4√2 ∙
2
=> S9 =
=
0
sin 45
28.
РАСЧЁТ ФЕРМF1=2кН G
2
RAX (-2)A
5
3
1
a
C
E
6
D
4
a
9
7
8
a
B
a
F2=5кН RBY (4)
RAY (1)
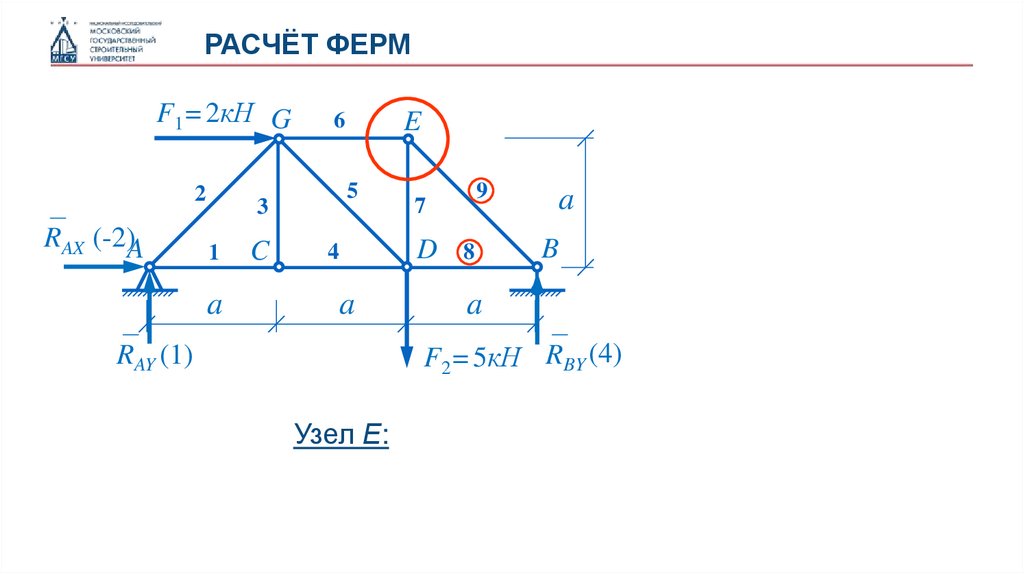
Узел Е:
29.
РАСЧЁТ ФЕРМУзел Е:
y
E
450
S6
S7
x
S9 = – 4√2
∑ Fkx= 0 : – S6 + S9 cos 450= 0;
∑ Fky= 0 : – S7 – S9 sin 450 = 0.
√2
= – 4 (кН);
=> S6 = S9 cos 450 = – 4√2 ∙
2
√2
0
= 4 (кН).
=
4√2
∙
=> S7 = – S9 sin 45
2
30.
РАСЧЁТ ФЕРМF1=2кН G
2
RAX (-2)A
5
3
1
a
C
E
6
D
4
a
9
7
8
a
B
a
F2=5кН RBY (4)
RAY (1)
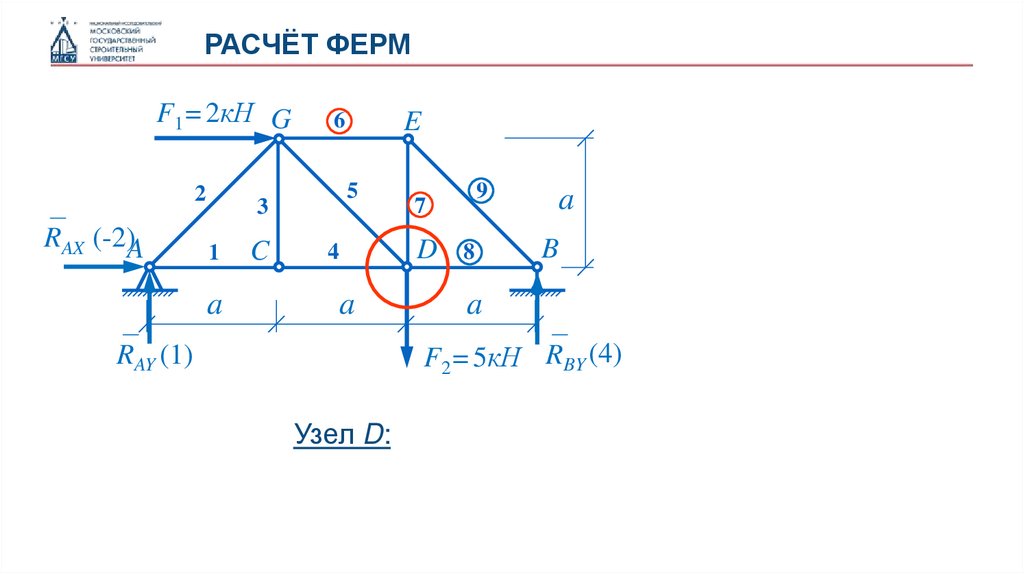
Узел D:
31.
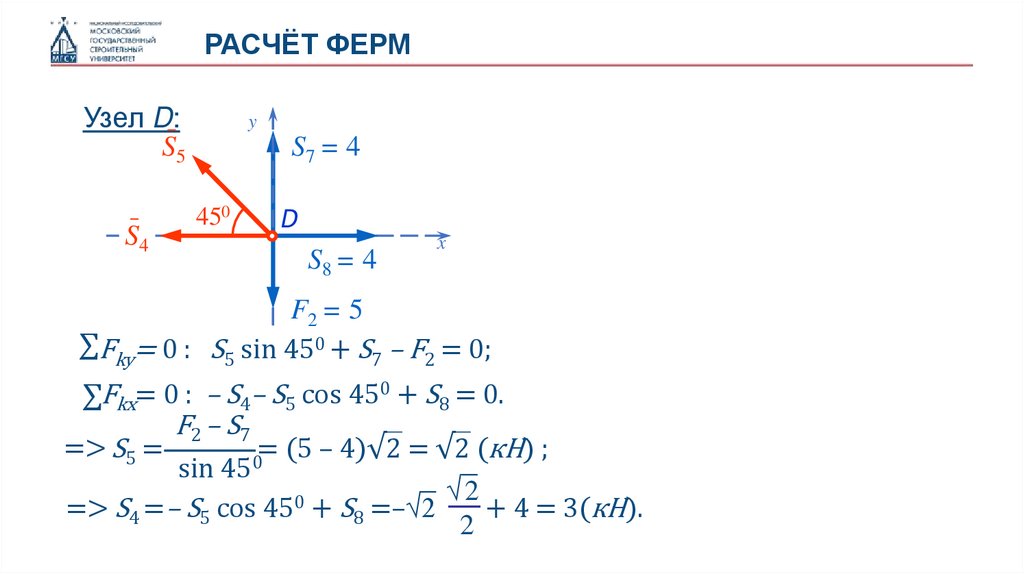
РАСЧЁТ ФЕРМУзел D:
S5
S4
y
S7 = 4
450
D
S8 = 4
x
F2 = 5
∑Fky= 0 : S5 sin 450 + S7 – F2 = 0;
∑Fkx= 0 : – S4– S5 соs 450 + S8 = 0.
=> S5 =
F 2 – S7
= (5 – 4)√2 = √2 (кН) ;
sin 450
√2
=> S4 =– S5 соs 450 + S8 =–√2
+ 4 = 3(кН).
2
32.
РАСЧЁТ ФЕРМF1=2кН G
2
RAX (-2)A
5
3
1
a
C
E
6
D
4
a
9
7
8
a
B
a
F2=5кН RBY (4)
RAY (1)
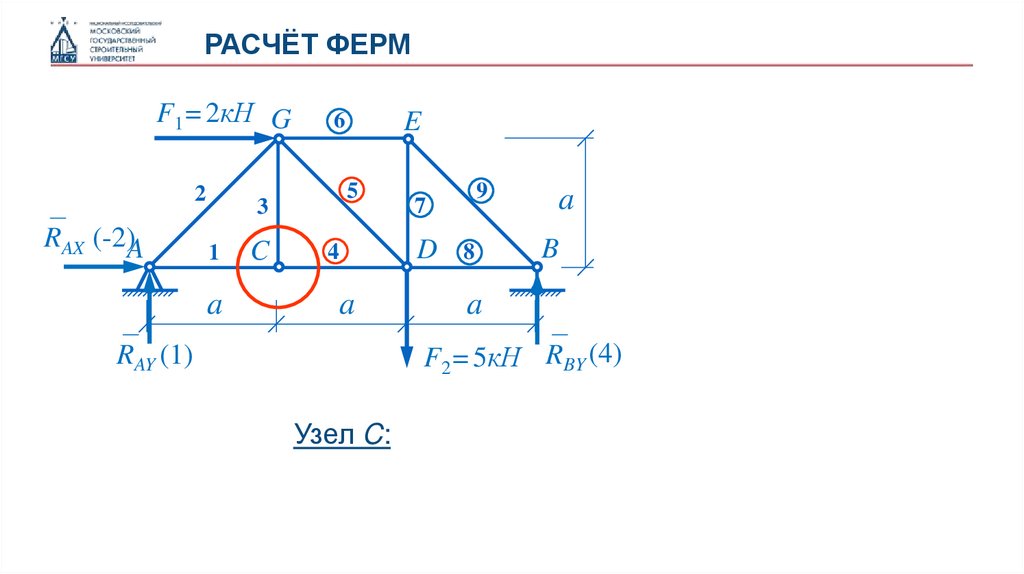
Узел C:
33.
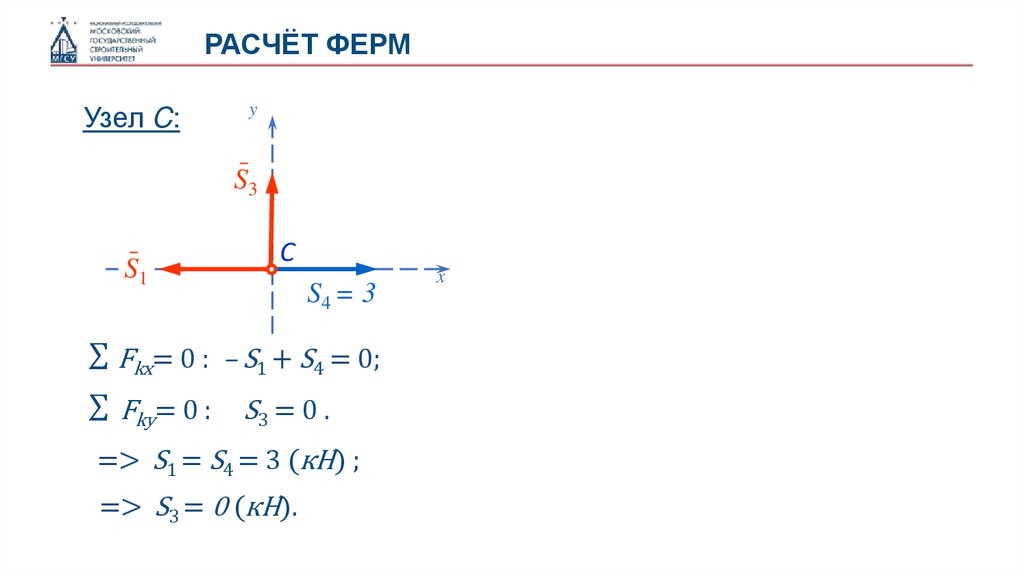
РАСЧЁТ ФЕРМУзел C:
y
S3
S1
С
S4 = 3
∑ Fkx= 0 : – S1 + S4 = 0;
∑ Fky= 0 :
S3 = 0 .
=> S1 = S4 = 3 (кН) ;
=> S3 = 0 (кН).
x
34.
РАСЧЁТ ФЕРМF1=2кН G
2
RAX (-2)A
5
3
1
a
C
E
6
D
4
a
9
7
8
a
B
a
F2=5кН RBY (4)
RAY (1)
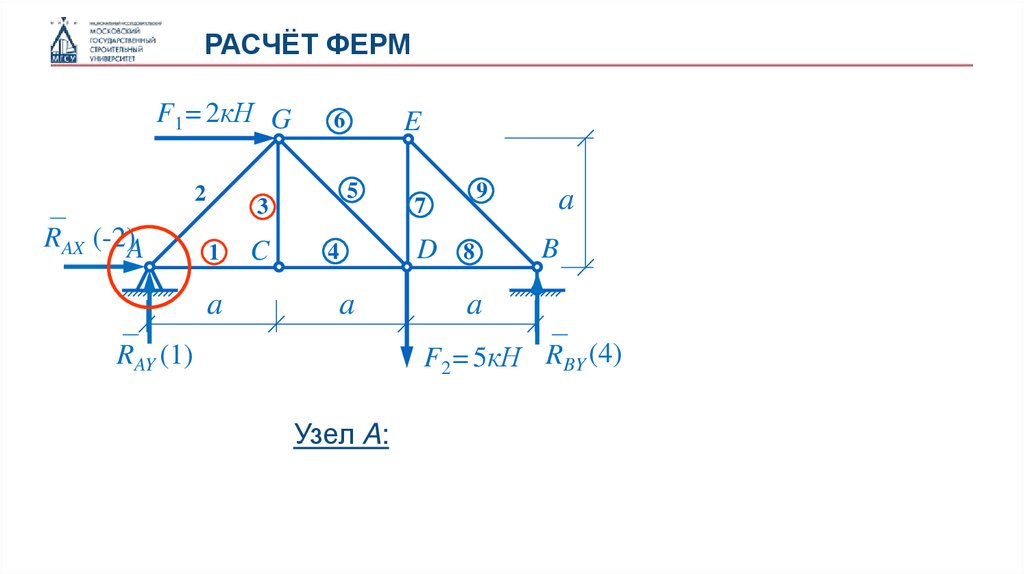
Узел A:
35.
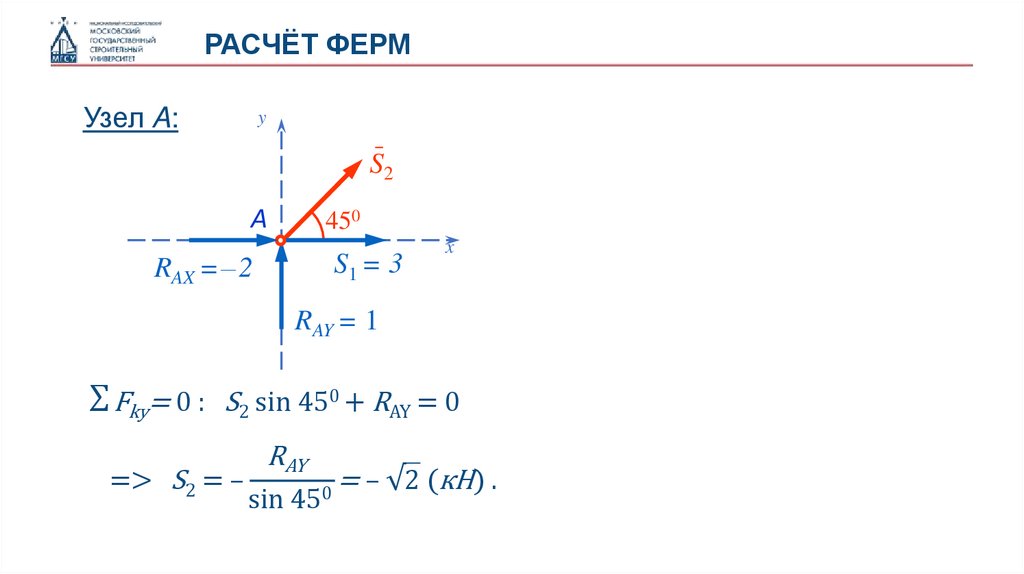
РАСЧЁТ ФЕРМУзел A:
y
S2
А
450
S1 = 3
RAX =–2
x
RAY = 1
∑ Fky= 0 : S2 sin 450 + RAY = 0
=> S2 = –
RAY
sin 450
= – √2 (кН) .
36.
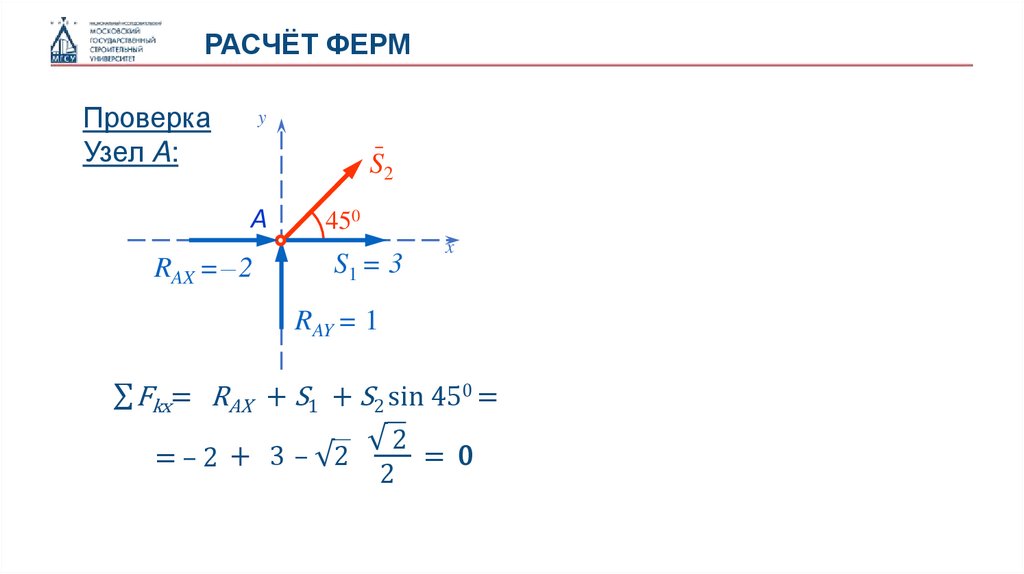
РАСЧЁТ ФЕРМПроверка
Узел A:
y
S2
А
RAX =–2
450
S1 = 3
x
RAY = 1
∑ Fkx= RAX + S1 + S2 sin 450 =
= – 2 + 3 – √2
√2
= 0
2
37.
РАСЧЁТ ФЕРМF1=2кН G
2
RAX (-2)A
5
3
1
a
C
E
6
D
4
a
9
7
8
a
B
a
F2=5кН RBY (4)
RAY (1)
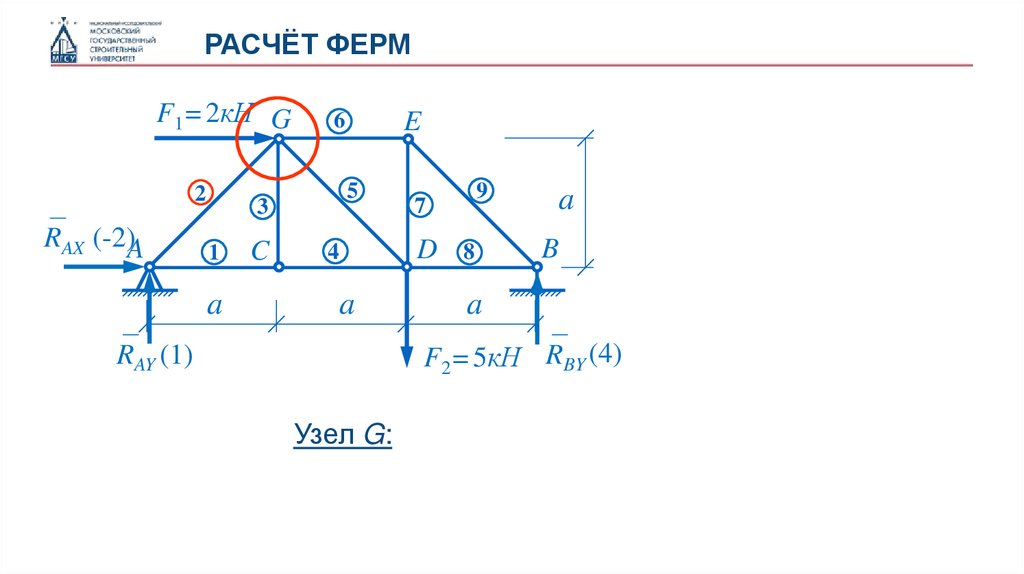
Узел G:
38.
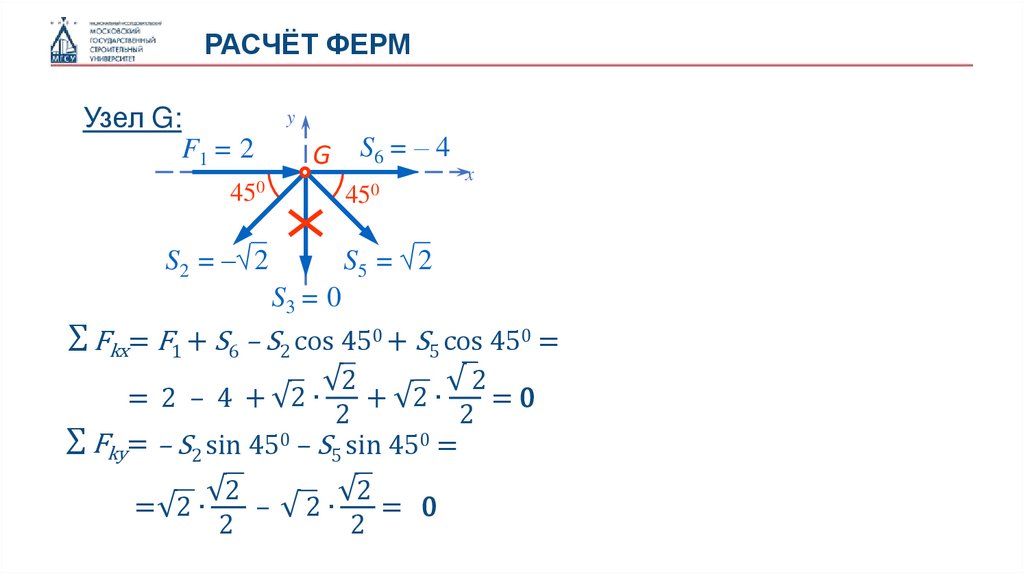
РАСЧЁТ ФЕРМУзел G:
F1 = 2
y
G
450
S6 = – 4
450
S2 = –√2
x
S5 = √ 2
S3 = 0
∑ Fkx= F1 + S6 – S2 cos 450 + S5 cos 450 =
√2
√2
+ √2 ∙
=0
2
2
∑ Fky= – S2 sin 450 – S5 sin 450 =
= 2 – 4 + √2 ∙
= √2 ∙
√2
√2
– √2∙
= 0
2
2
39.
РАСЧЁТ ФЕРМ?
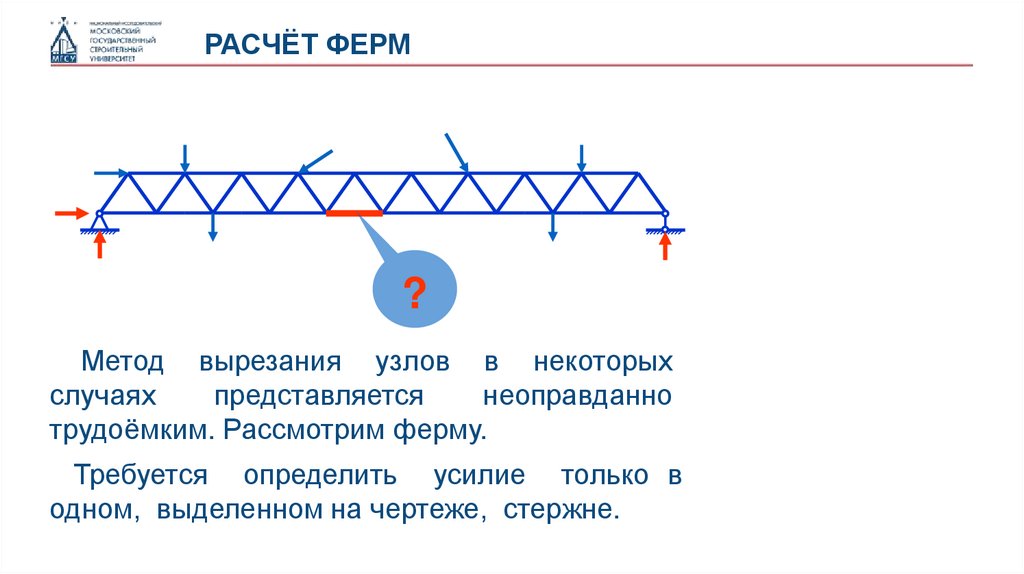
Метод вырезания узлов в некоторых
случаях
представляется
неоправданно
трудоёмким. Рассмотрим ферму.
Требуется определить усилие только в
одном, выделенном на чертеже, стержне.
40.
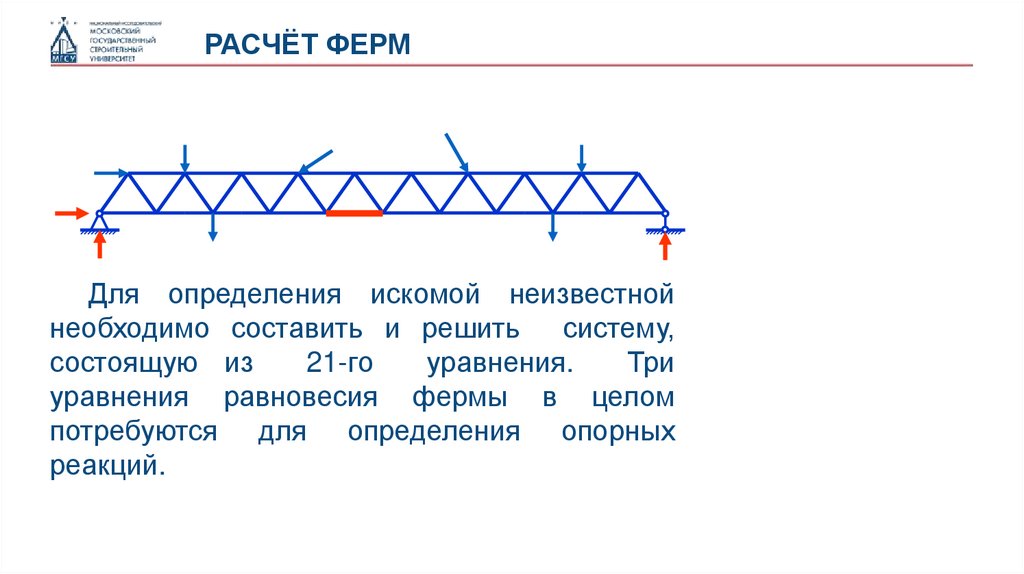
РАСЧЁТ ФЕРМДля определения искомой неизвестной
необходимо составить и решить систему,
состоящую из
21-го
уравнения.
Три
уравнения равновесия фермы в целом
потребуются для определения опорных
реакций.
41.
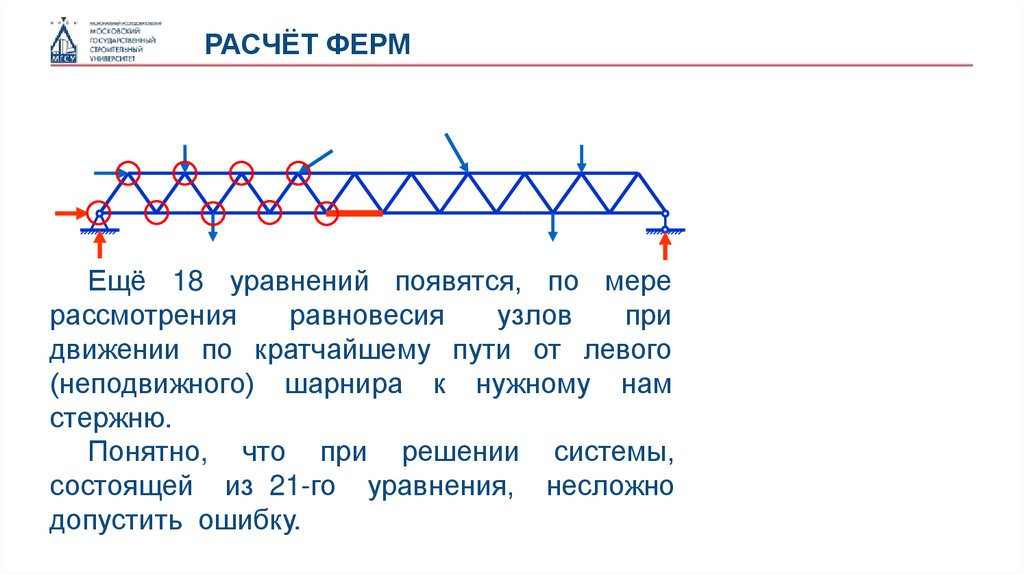
РАСЧЁТ ФЕРМЕщё 18 уравнений появятся, по мере
рассмотрения
равновесия
узлов
при
движении по кратчайшему пути от левого
(неподвижного) шарнира к нужному нам
стержню.
Понятно, что при решении системы,
состоящей из 21-го уравнения, несложно
допустить ошибку.
42.
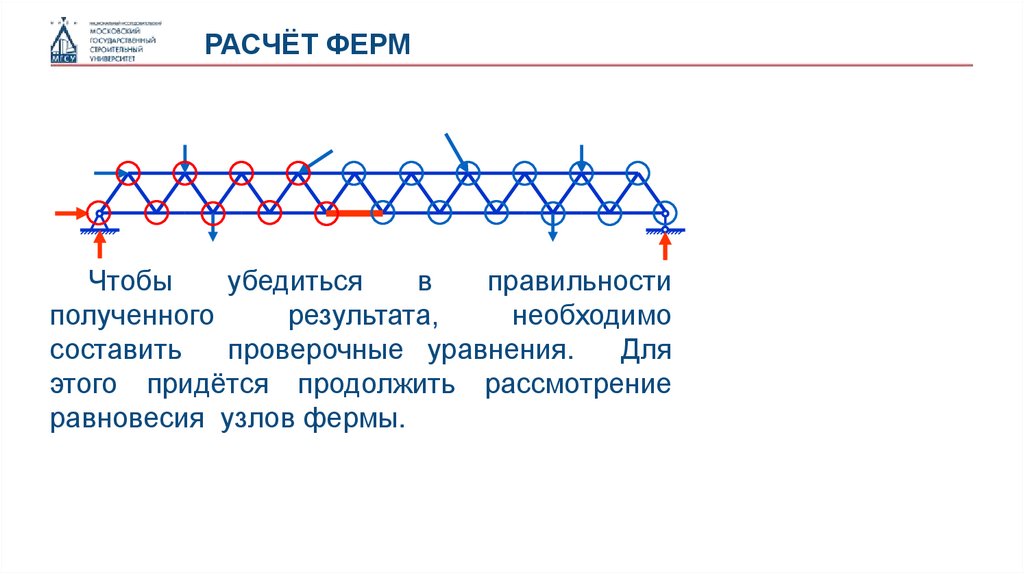
РАСЧЁТ ФЕРМЧтобы
убедиться
в
правильности
полученного
результата,
необходимо
составить
проверочные уравнения.
Для
этого придётся продолжить рассмотрение
равновесия узлов фермы.
43.
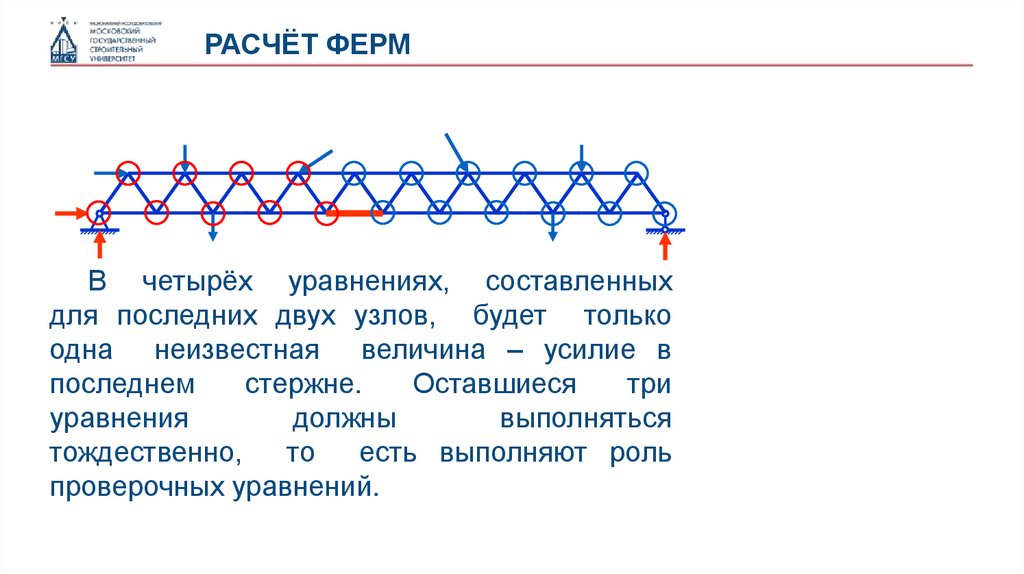
РАСЧЁТ ФЕРМВ четырёх уравнениях, составленных
для последних двух узлов, будет только
одна неизвестная величина – усилие в
последнем
стержне.
Оставшиеся
три
уравнения
должны
выполняться
тождественно,
то
есть выполняют роль
проверочных уравнений.
44.
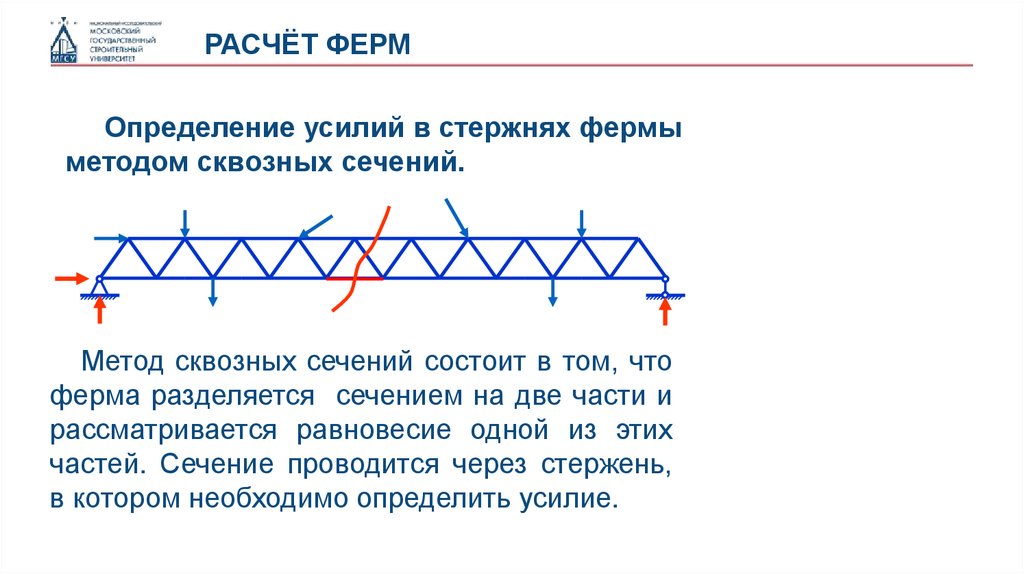
РАСЧЁТ ФЕРМОпределение усилий в стержнях фермы
методом сквозных сечений.
Метод сквозных сечений состоит в том, что
ферма разделяется сечением на две части и
рассматривается равновесие одной из этих
частей. Сечение проводится через стержень,
в котором необходимо определить усилие.
45.
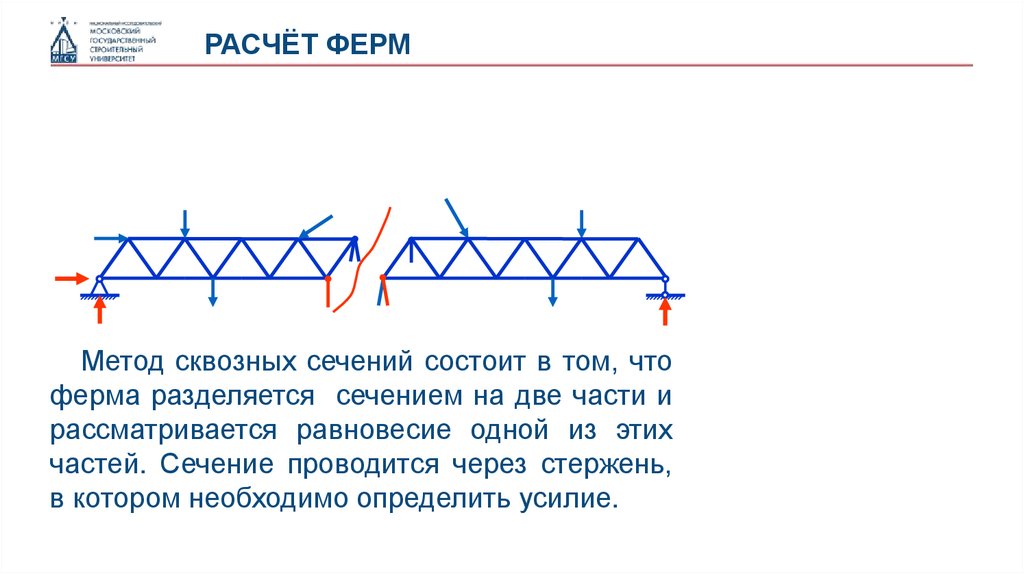
РАСЧЁТ ФЕРММетод сквозных сечений состоит в том, что
ферма разделяется сечением на две части и
рассматривается равновесие одной из этих
частей. Сечение проводится через стержень,
в котором необходимо определить усилие.
46.
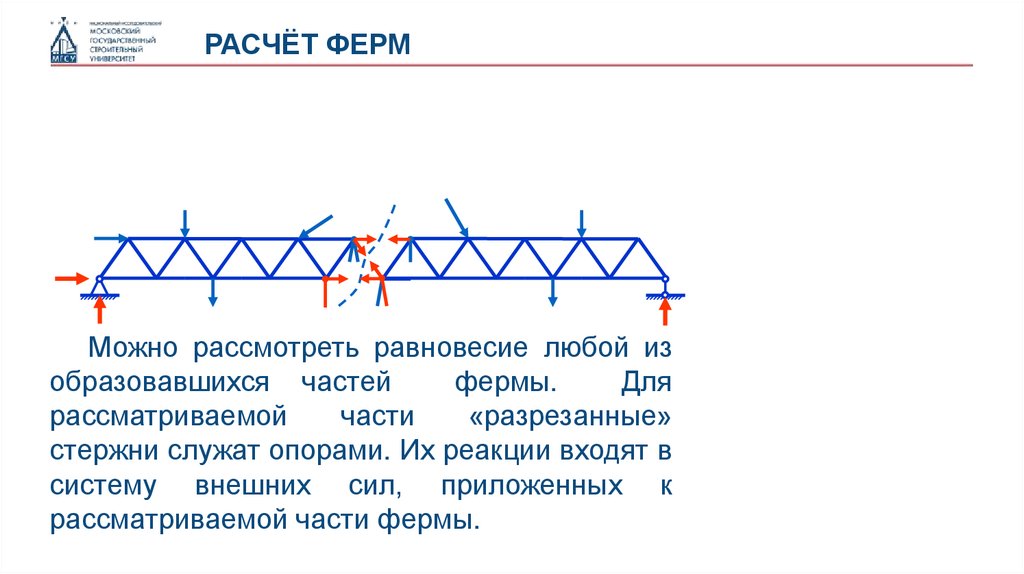
РАСЧЁТ ФЕРММожно рассмотреть равновесие любой из
образовавшихся частей
фермы.
Для
рассматриваемой
части
«разрезанные»
стержни служат опорами. Их реакции входят в
систему внешних сил, приложенных к
рассматриваемой части фермы.
47.
РАСЧЁТ ФЕРММожно рассмотреть равновесие любой из
образовавшихся частей
фермы.
Для
рассматриваемой
части
«разрезанные»
стержни служат опорами. Их реакции входят в
систему внешних сил, приложенных к
рассматриваемой части фермы.
48.
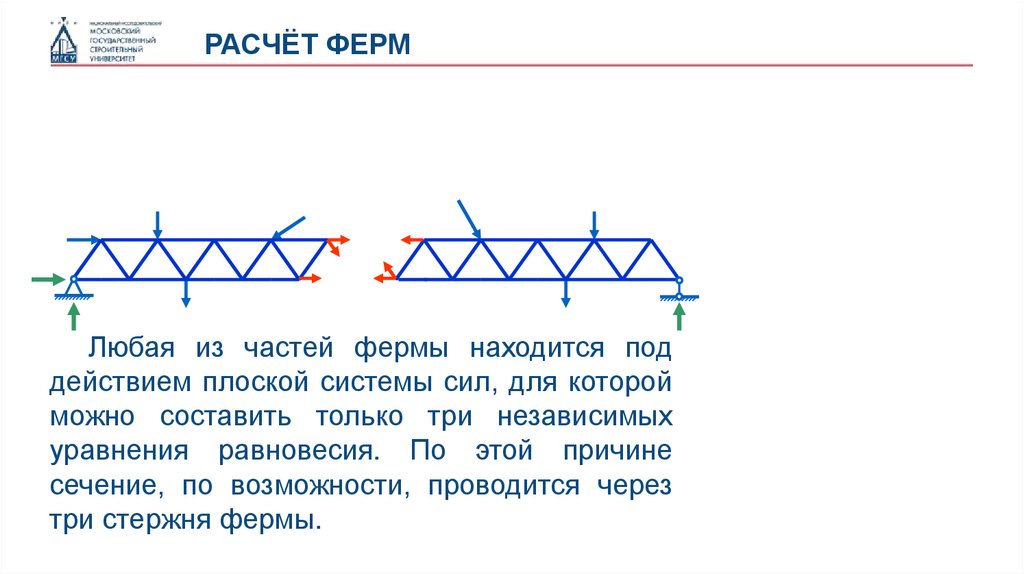
РАСЧЁТ ФЕРМЛюбая из частей фермы находится под
действием плоской системы сил, для которой
можно составить только три независимых
уравнения равновесия. По этой причине
сечение, по возможности, проводится через
три стержня фермы.
49.
РАСЧЁТ ФЕРМF1=2кН G
2
RAX (-2)A
a
RAY (1)
5
3
1
C
E
6
4
a
9
7
D
8
a
B
a
F2=5кН RBY (4)
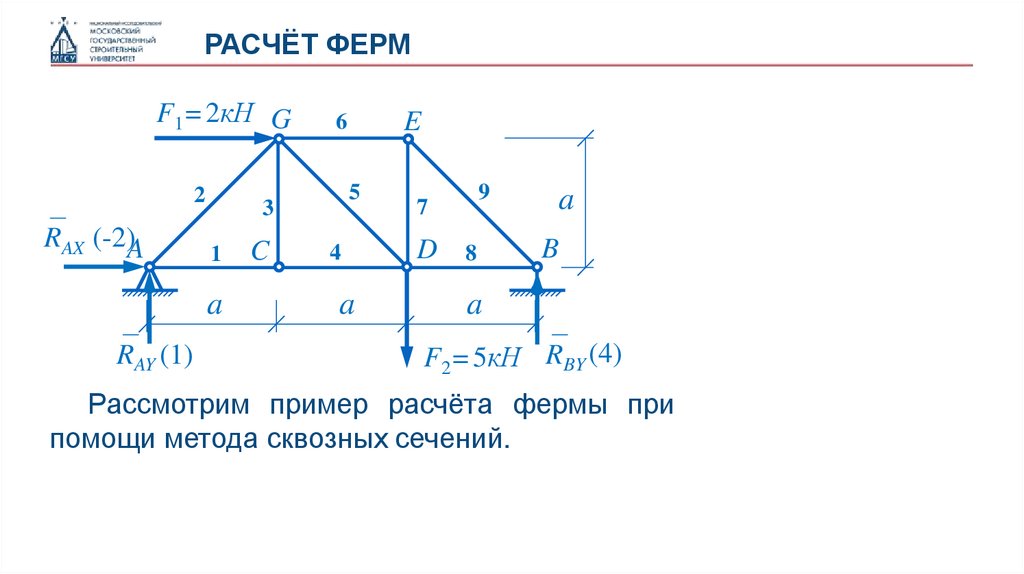
Рассмотрим пример расчёта фермы при
помощи метода сквозных сечений.
50.
РАСЧЁТ ФЕРМF1=2кН G
2
RAX (-2)A
a
RAY (1)
5
3
1
C
E
6
4
a
9
7
D
8
a
B
a
F2=5кН RBY (4)
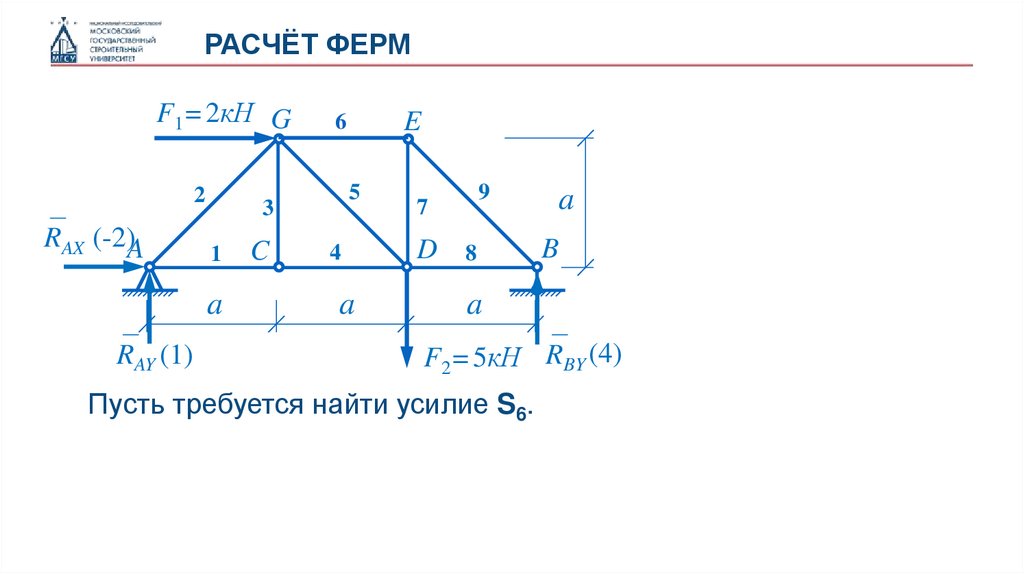
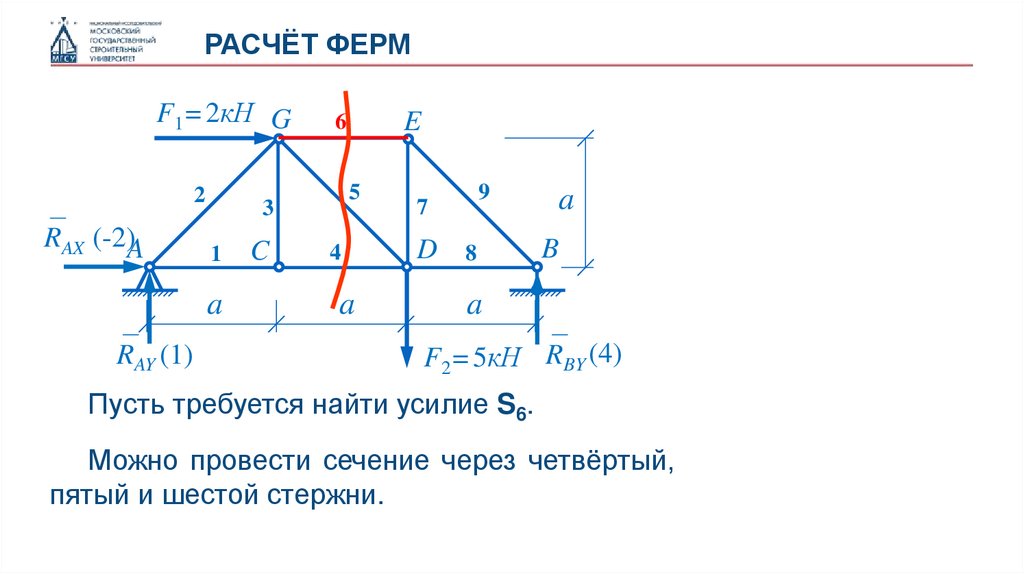
Пусть требуется найти усилие S6.
51.
РАСЧЁТ ФЕРМF1=2кН G
2
RAX (-2)A
a
RAY (1)
5
3
1
C
E
6
4
a
9
7
D
8
a
B
a
F2=5кН RBY (4)
Пусть требуется найти усилие S6.
Можно провести сечение через четвёртый,
пятый и шестой стержни.
52.
РАСЧЁТ ФЕРМF1=2кН G
2
RAX (-2)A
1
a
RAY (1)
E
3
7
C
D
a
9
8
a
B
a
F2=5кН RBY (4)
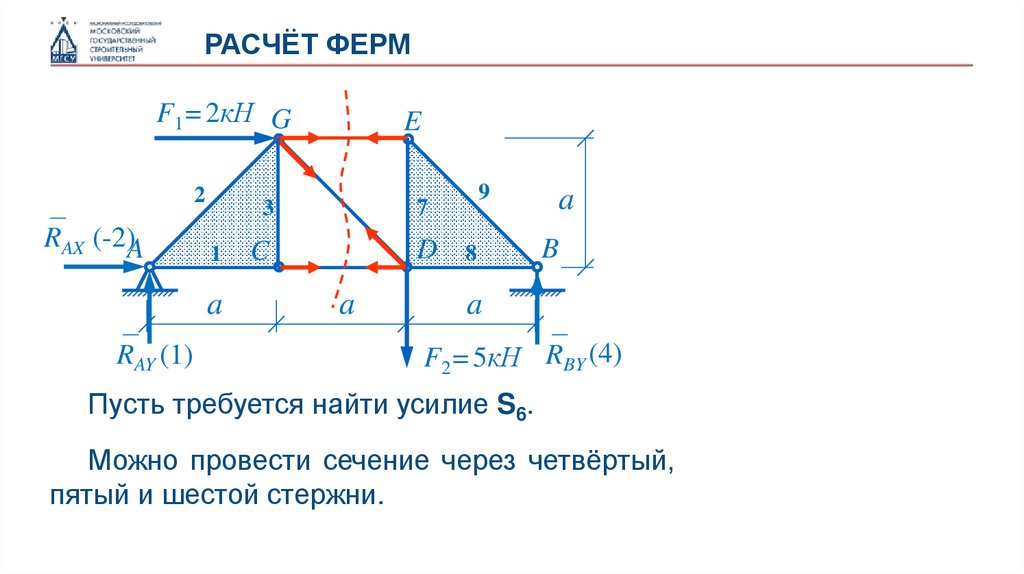
Пусть требуется найти усилие S6.
Можно провести сечение через четвёртый,
пятый и шестой стержни.
53.
РАСЧЁТ ФЕРМF1=2кН G
2
RAX (-2)A
a
RAY (1)
5
3
1
C
E
6
4
a
9
7
D
8
a
B
a
F2=5кН RBY (4)
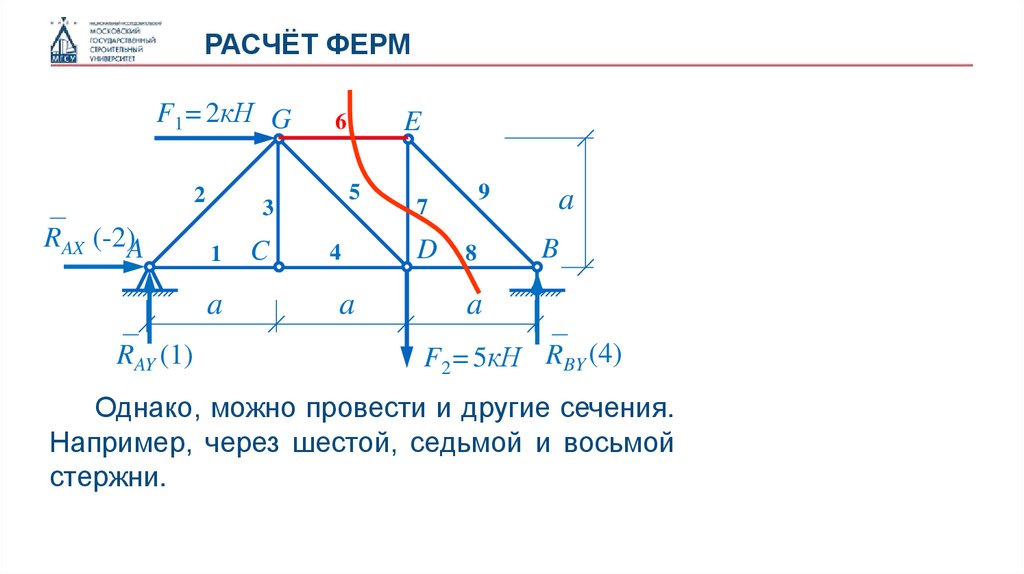
Однако, можно провести и другие сечения.
Например, через шестой, седьмой и восьмой
стержни.
54.
РАСЧЁТ ФЕРМF1=2кН G
2
RAX (-2)A
a
RAY (1)
5
3
1
C
E
6
4
a
9
7
D
8
a
B
a
F2=5кН RBY (4)
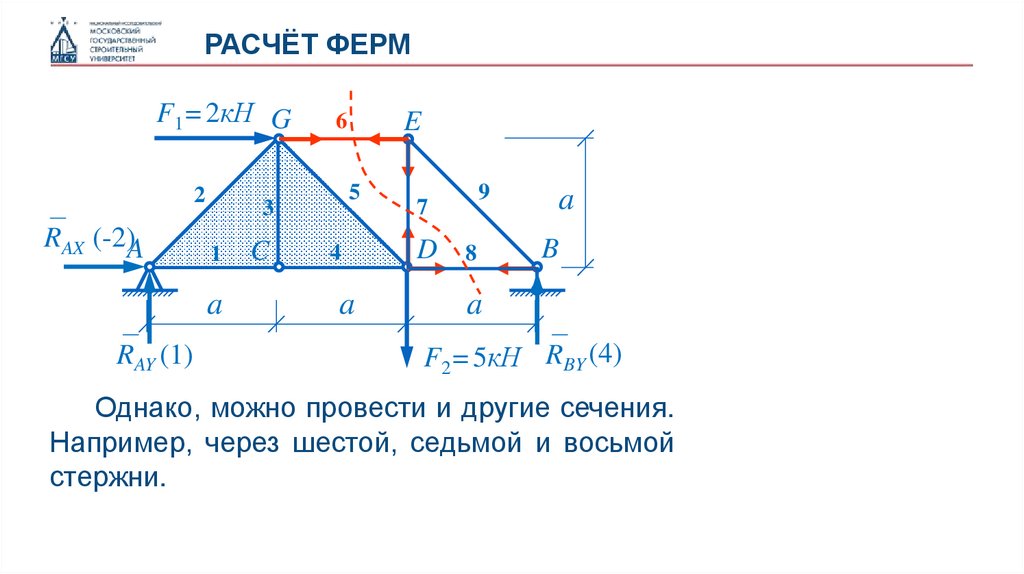
Однако, можно провести и другие сечения.
Например, через шестой, седьмой и восьмой
стержни.
55.
РАСЧЁТ ФЕРМF1=2кН G
2
RAX (-2)A
a
RAY (1)
5
3
1
C
E
6
4
a
9
7
D
8
a
B
a
F2=5кН RBY (4)
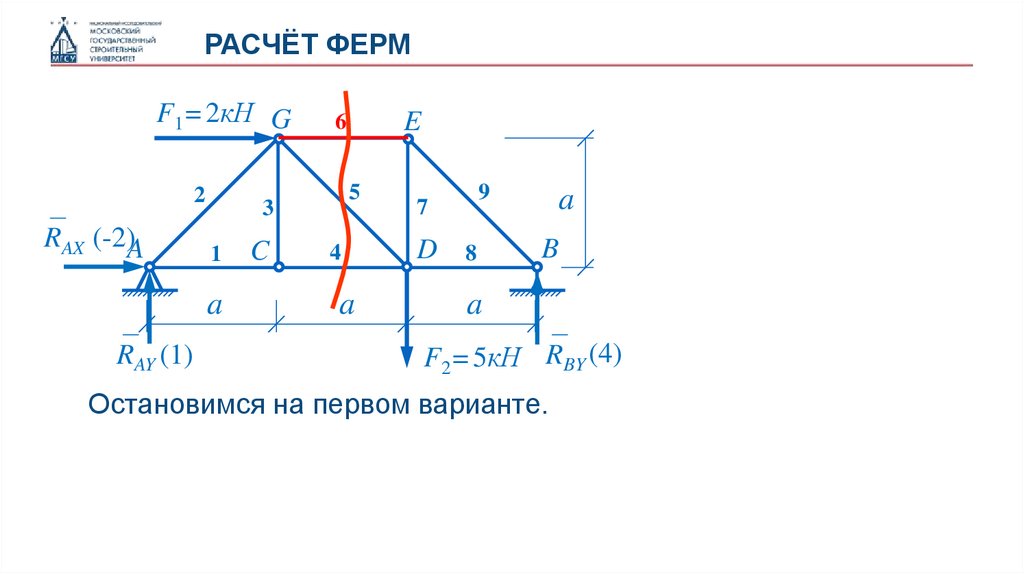
Остановимся на первом варианте.
56.
РАСЧЁТ ФЕРМF1=2кН G
2
RAX (-2)A
1
E
3
7
C
D
a
RAY (1)
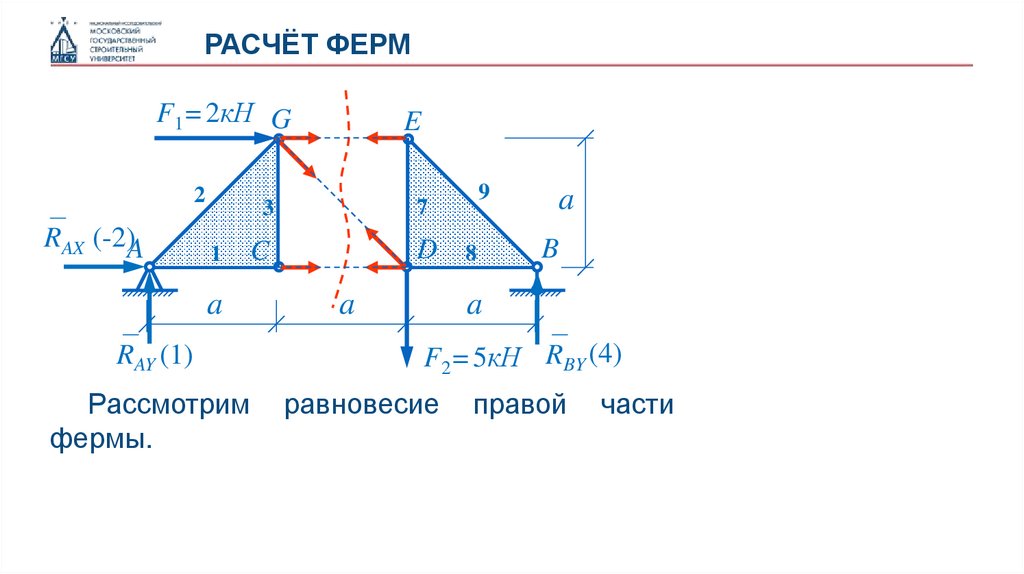
Рассмотрим
фермы.
a
9
8
a
B
a
F2=5кН RBY (4)
равновесие
правой
части
57.
РАСЧЁТ ФЕРМВсего
неизвестных
величин три. Определить
нужно только одну из них
– S6 . Линии действия сил
S4 и S5 проходят через
точку D. Поэтому для
определения
S6
составляем
уравнение
равенства нулю суммы
моментов
всех
сил
системы
относительно
точки D.
S6
E
a
S5
S4
B
D
a
F2= 5кН
RBY(4)
58.
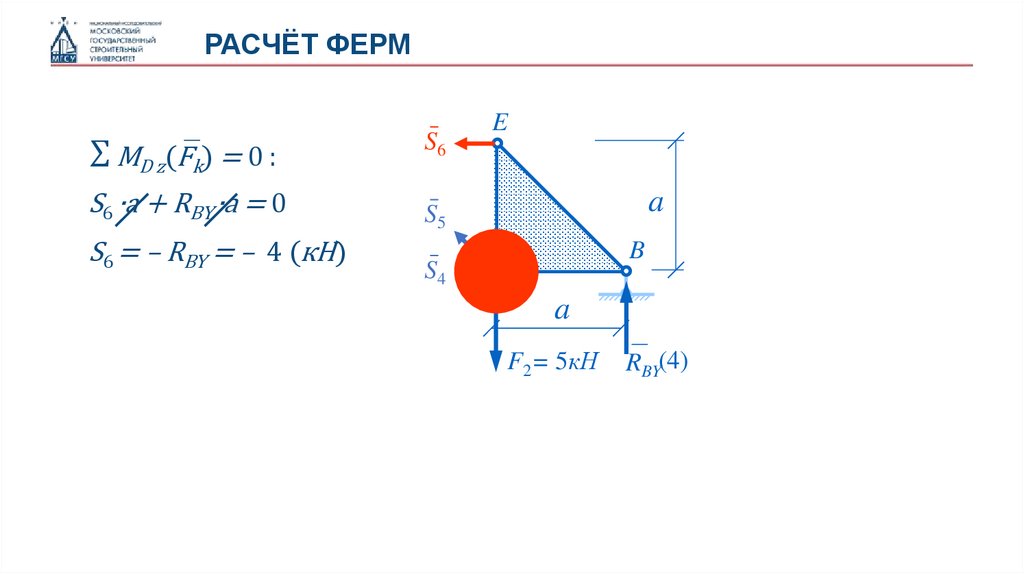
РАСЧЁТ ФЕРМ∑ MD z(Fk) = 0 :
S6
S6 ∙a + RBY ∙a = 0
S5
S6 = – RBY = – 4 (кН)
S4
E
a
B
D
a
F2= 5кН
RBY(4)
59.
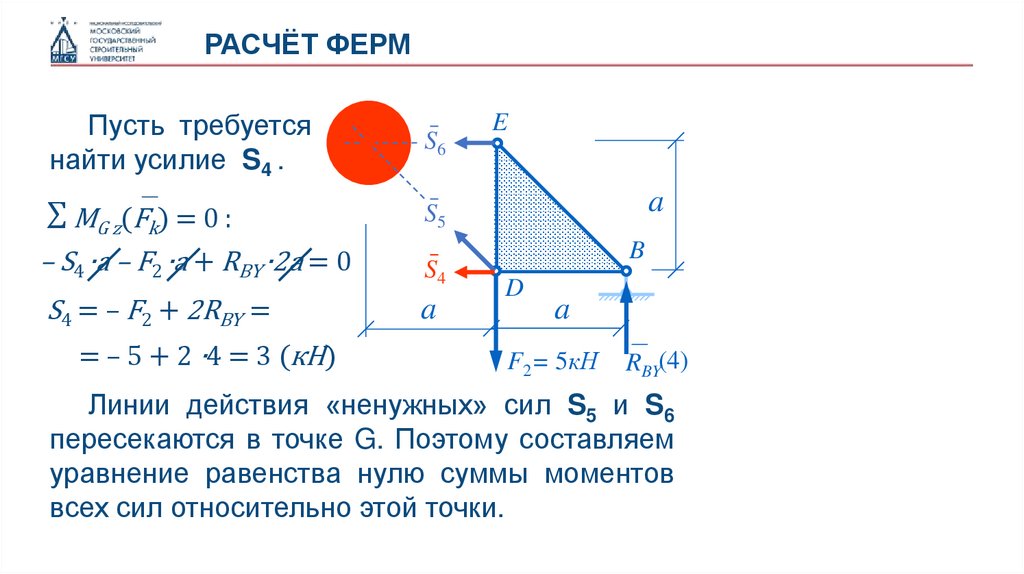
РАСЧЁТ ФЕРМПусть требуется
найти усилие S4 .
G
S6
∑ MG z(Fk) = 0 :
S5
– S4 ∙a – F2 ∙a + RBY ∙2a = 0
S4
S4 = – F2 + 2RBY =
a
= – 5 + 2 ∙4 = 3 (кН)
E
a
B
D
a
F2= 5кН
RBY(4)
Линии действия «ненужных» сил S5 и S6
пересекаются в точке G. Поэтому составляем
уравнение равенства нулю суммы моментов
всех сил относительно этой точки.
60.
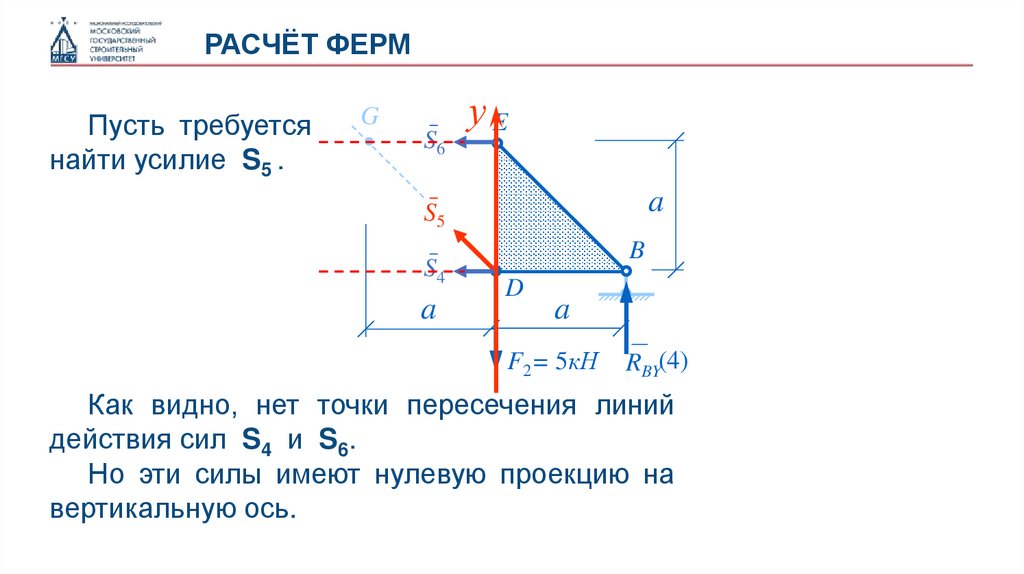
РАСЧЁТ ФЕРМПусть требуется
найти усилие S5 .
G
S6
уE
a
S5
S4
a
B
D
a
F2= 5кН
RBY(4)
Как видно, нет точки пересечения линий
действия сил S4 и S6.
Но эти силы имеют нулевую проекцию на
вертикальную ось.
61.
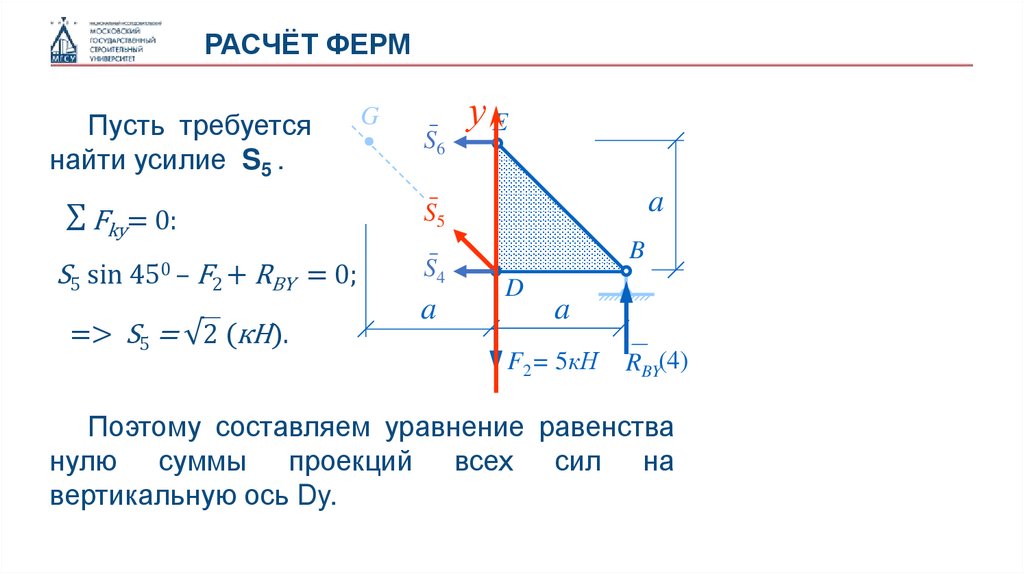
РАСЧЁТ ФЕРМПусть требуется
найти усилие S5 .
∑ Fky= 0:
S5
sin 450 – F
G
S6
уE
a
S5
2 + RBY = 0;
=> S5 = √2 (кН).
S4
a
B
D
a
F2= 5кН
RBY(4)
Поэтому составляем уравнение равенства
нулю суммы проекций всех сил на
вертикальную ось Dy.
62.
СПАСИБОЗА ВНИМАНИЕ!












 mathematics
mathematics








