Similar presentations:
Показательная функция и показательные уравнения
1.
LOGOПоказательная функция и
показательные уравнения
Для добавления
Мочалов.
текста щёлкните
А
мышью
Чистяков. Д
2.
www.themegallery.comПоказательная функция
Показательная функция — функция обычно
обозначаемая y = a x, где а - некоторое вещественное
число (a>0, a ≠ 0), а x — переменная. Если в качестве
a (называемого также основанием) стоит число e, то
функция называется экспонентой.
Company Logo
3.
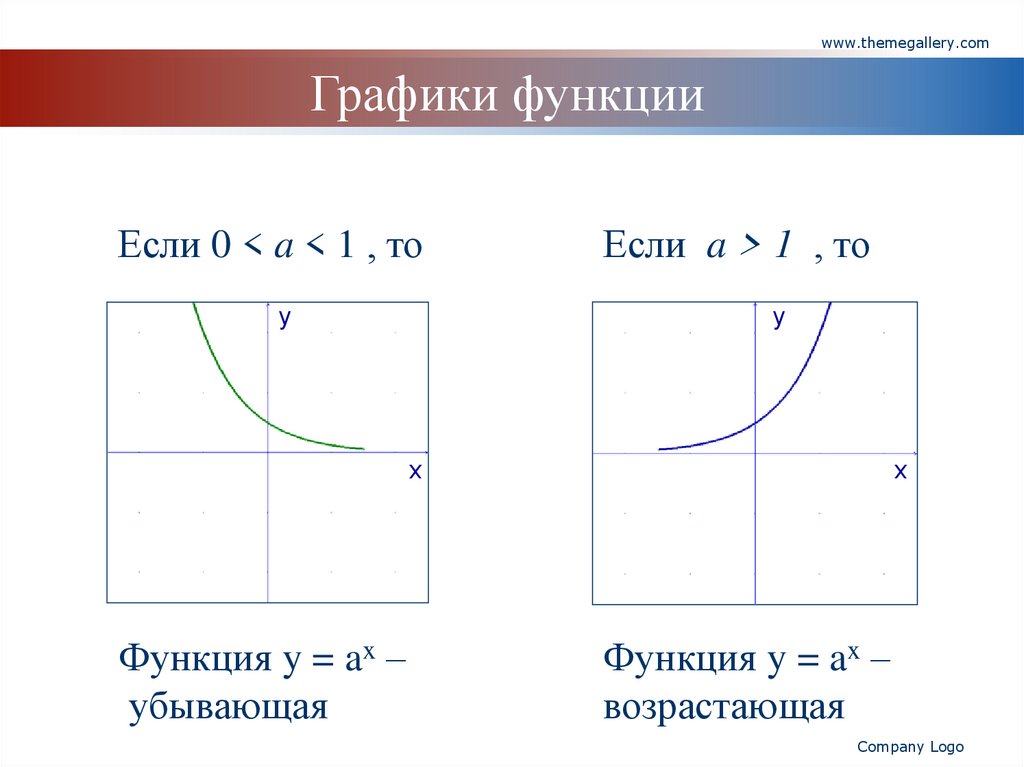
www.themegallery.comГрафики функции
Если 0 < a < 1 , то
у
Если a > 1 , то
у
х
Функция y = ax –
убывающая
х
Функция y = ax –
возрастающая
Company Logo
4.
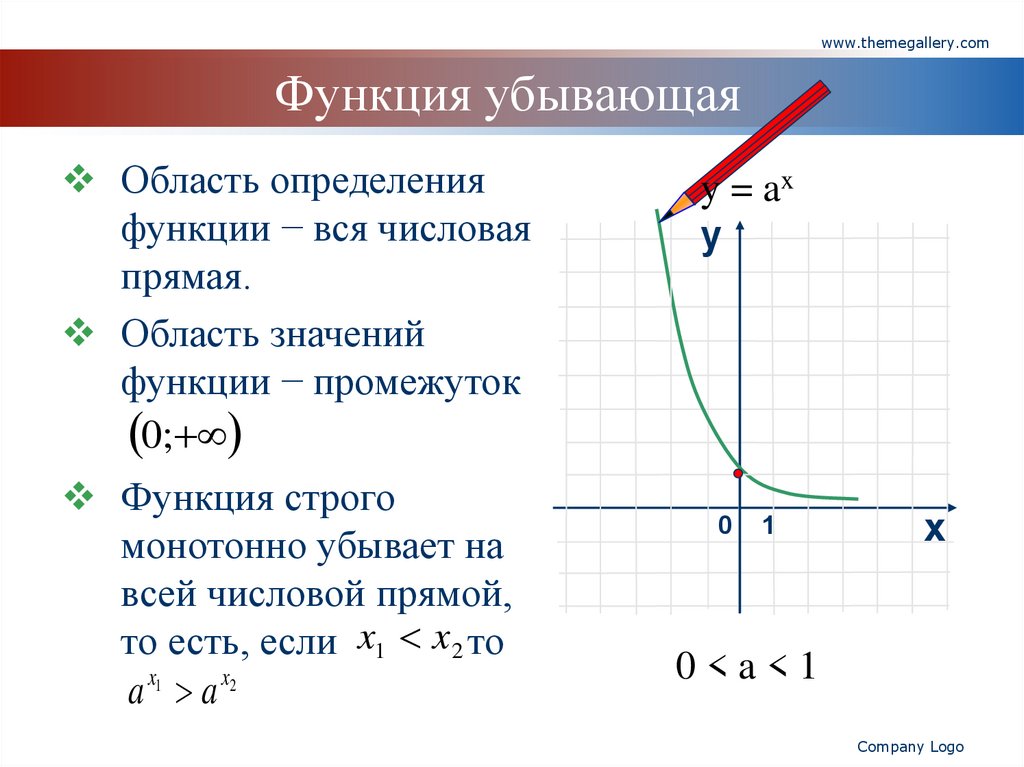
www.themegallery.comФункция убывающая
Область определения
функции − вся числовая
прямая.
Область значений
функции − промежуток
0;
Функция строго
монотонно убывает на
всей числовой прямой,
то есть, если x1 x 2 то
a x1 a x2
y = ax
у
0
1
х
0<a<1
Company Logo
5.
www.themegallery.comФункция возрастающая
y = ax
у
Область определения
функции − вся числовая
прямая.
Область значений
функции− промежуток
0;
0
1
a>1
Функция строго
х
монотонно возрастает на
всей числовой прямой,
то есть, если x1 x2 то
a x1 a x2
Company Logo
6.
www.themegallery.comПреобразования показательной функции
Симметричное преобразование относительно оси x
Симметричное преобразование относительно оси y
Параллельный перенос вдоль оси y
Сжатие и растяжение вдоль оси х
Взаимно обратной к показательной функции
является логарифмическая функция.
Company Logo
7.
www.themegallery.comСвойства показательных функций
a x1a x 2
a
a
x1 x 2
x
a
a
x1 x 2
x1 x 2
для всех x1, x2.
для всех x1, x2.
1
x для любого x .
a
x
n
n a x a для любого x и любого n , n 1.
Company Logo
8.
www.themegallery.comСвойства показательных функций
ab x
a x b x для любых a, b 0, a, b 1.
x
x
a
a
x для любых a, b 0, a, b 1.
b
b
a a
x1
x2
x1 x2
Company Logo
9.
www.themegallery.comПоказательные уравнения
Уравнение, которое содержит неизвестное в
показателе степени, называется показательным
уравнением.
Самое простое показательное уравнение имеет
вид ax = b, где a > 0, a ≠ 1.
Company Logo
10.
www.themegallery.comРешение показательных уравнений
Решение большинства показательных уравнений
после некоторых преобразований сводится
к решению одного или нескольких показательных
f(x)
g(x)
f(x)
(a 0, a 1),
a
a
a
b
уравнений вида
или
Последнее из которых равносильно уравнению
f(x) = g(x).
Company Logo
11.
www.themegallery.comМетоды решения
Основными методами решения
показательных уравнений являются:
Метод группировки и разложения
на множители;
Замена переменной (позволяющий свести
уравнение к алгебраическому (как правило,
квадратному) уравнению)
Company Logo
12.
www.themegallery.comЗамена переменной
Уравнение a ·l2x b ·lx c 0 сводится
к квадратному уравнению заменой
y l x , y 0 . Для решения однородного
2x
x
2x
p
·a
q
·(ab)
r
·b
0
уравнения вида
2x
b
нужно обе его части разделить на
Заметим, что по свойству показательной
2x
b
0 ни при каких x.
функции
Company Logo
13.
www.themegallery.comСледствие
После
деления
получится уравнение
2x
x
a
a
p · q· r 0 которое заменой
b
x
b
a
y сводится к квадратному уравнению
b
относительно y.
Company Logo
14.
www.themegallery.comПримеры
Решим уравнение 35 x 2 81x 1
Решение. Данное уравнение равносильно
уравнению 35x 2 34x-4 5x 2 4x - 4 -6
Ответ:-6
Company Logo
15.
www.themegallery.comПримеры
Решим уравнение 4 2x 1 3·42x-1 - 5·42x -64.
Решение. Вынесем за скобки общий
множитель 4 2x - 1 в левой части
4 2x-1 (16 3 - 20) -64 4 2x-1 -64 4 2 x-1 64 2 x 1 3 x 2.
Ответ: 2
Company Logo
16.
www.themegallery.comВыводы
Рассмотрены определение и основные свойства
показательной функции
Рассмотрены показательные уравнения
Приведены и подробно рассмотрены примеры
задач на показательные функции
Company Logo














 mathematics
mathematics








