Изучение статистических характеристик в курсе школьной математики

1.

Изучение статистических характеристик в
курсе школьной математики

2.

Среднее арифметическое
Определение: Средним арифметическим
нескольких чисел называется число, равное
отношению суммы этих чисел к их
количеству.

3.

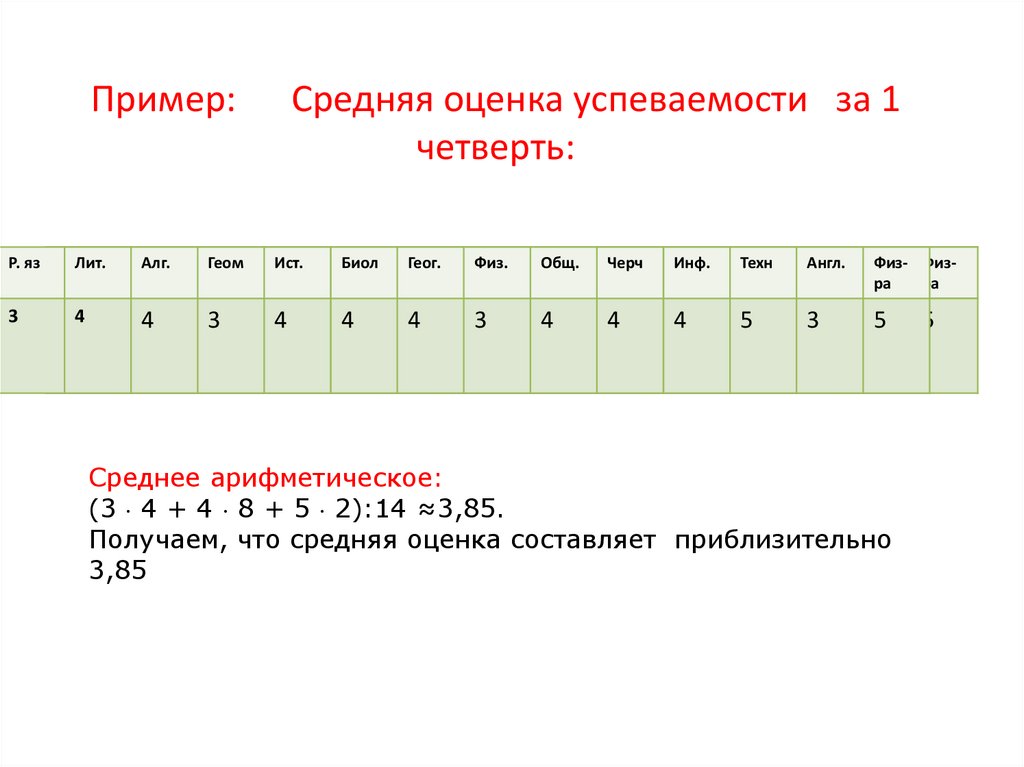
Пример:
Средняя оценка успеваемости за 1
четверть:
Р. яз Р. яз
Лит.
Лит.
Алг.
Алг.
Геом Геом
Ист.
Ист.
Биол Биол
Геог. Геог.
Физ. Физ.
Общ. Общ.
Черч Черч
Инф. Инф.
Техн Техн
Англ. Англ.
Физ- Физра
ра
3
4 4
43
44
3 4
34
44
43
34
44
44
45
53
35
Среднее арифметическое:
(3 4 + 4 8 + 5 2):14 ≈3,85.
Получаем, что средняя оценка составляет приблизительно
3,85
5

4.

Мода (Мо)
Модой называется то число, которое в
данном числовом ряду встречается чаще
всего. В числовом ряду может быть одна
мода или несколько.
Например: Найти моду ряда чисел:
2,2,3,3,3,4,4,5,5,5,5,6,6,7. Чаще всего
встречается число 5, значит М = 5.
о

5.

Пример нахождения моды:
• В отделе мужской обуви универмага в
течение дня производился учет размеров
купленной обуви.
Были получены следующие результаты: 42, 40,
43, 39, 42, 42, 45, 41, 43, 43, 41, 42, 46, 40, 42,
42, 39, 42, 45, 42, 43, 42, 44, 41, 42.
Какой размер обуви наиболее распространен,
т.е. найти моду.
Чаще всего встречается 42 размер, значит М =
о
42

6.

Наибольшее и наименьшее
значение. Размах (А).
Определение: Разность между наибольшим и наименьшим
числом называется размахом набора чисел.
Урожай картофеля в сёлах А и В:
А
180
50
60
100
170
60
150
90
120
70
60
160
90
170
90
В
100
110
120
110
100
100
110
100
130
130
110
120
100
100
110
Самый большой урожай в селе А:180ц/га, самый маленький - 50 ц/га.
В селе В: самый большой – 130 ц/га, самый маленький – 100 ц/га.
Размах производства картофеля в селе А: 180 – 50 = 130,
в селе В: 130 – 100 = 30.

7.

Медиана (Ме)
Определение: Медианой набора чисел называют
такое число, которое разделяет набор на две
равные по численности части.
Прежде чем искать медиану ряда, нужно
упорядочить ряд чисел.

8.

Примеры нахождения медианы
Пример 1. Возьмём какой-нибудь набор различных чисел, например
1,4,7,9,11 - чётный ряд
Медианой в этом случае оказывается число, стоящее в точности
посередине, m=7.
Пример 2. Рассмотрим набор 1,3,6,11. – нечётный ряд Медианой этого
набора служит число, равное полусумме чисел, стоящих посередине:
(3+6):2=4,5
Медианой этого набора считают число 4,5.

9.

Среднее геометрическое
• Определение. Средним геометрическим
нескольких чисел называется квадратный
корень из произведения этих чисел.
Например: Даны числа: 2; 5; 10.
Ср. геометрическое = 2*5*10 =10

10.

Отклонения
Определение: отклонение – это разница между каждым
числом набора и средним арифметическим ряда
чисел.
Пример:
Возьмём набор чисел 1,6,7,9,12.
Вычислим среднее арифметическое: (1+6+7+9+12):5=7. Найдём
отклонение каждого числа от среднего арифметического:
1-7=-6, 6-7=-1, 7-7=0, 9-7=2, 12-7=5.
Сумма отклонений чисел от среднего арифметического этих
чисел равна нулю.

11.

Дисперсия-это величина, показывающая, как именно
и насколько сильно разбросаны значения
Определение: среднее арифметическое
квадратов отклонений от среднего значения
называется в статистике дисперсией набора
чисел.

12.

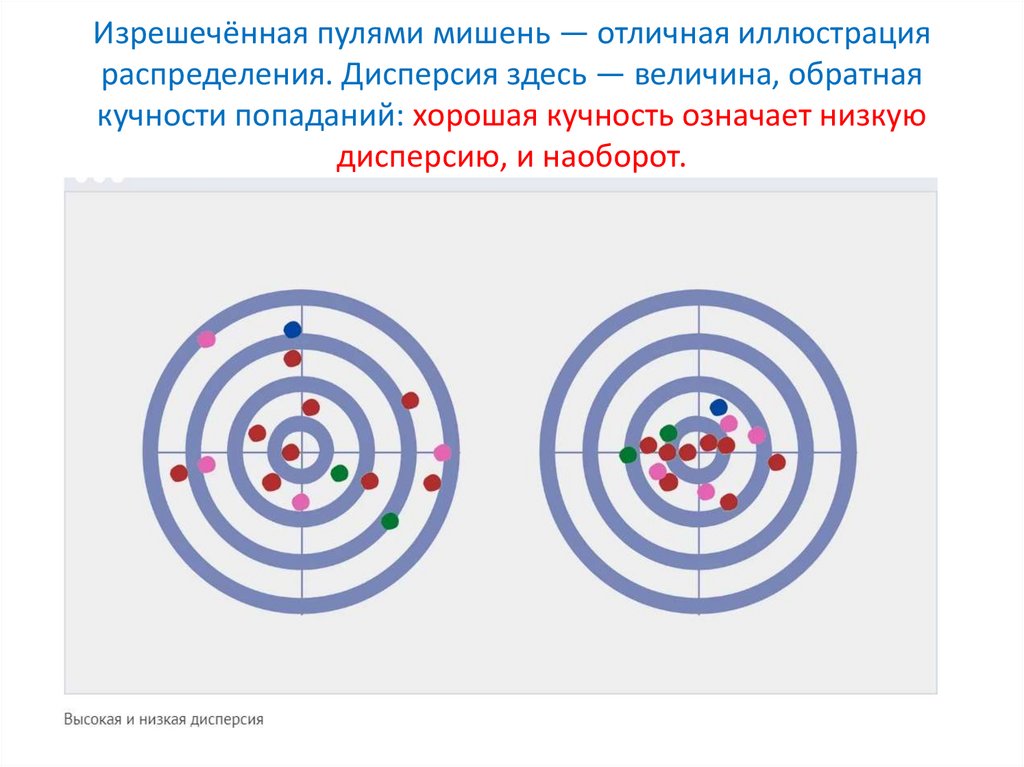
Изрешечённая пулями мишень — отличная иллюстрация
распределения. Дисперсия здесь — величина, обратная
кучности попаданий: хорошая кучность означает низкую
дисперсию, и наоборот.

13.

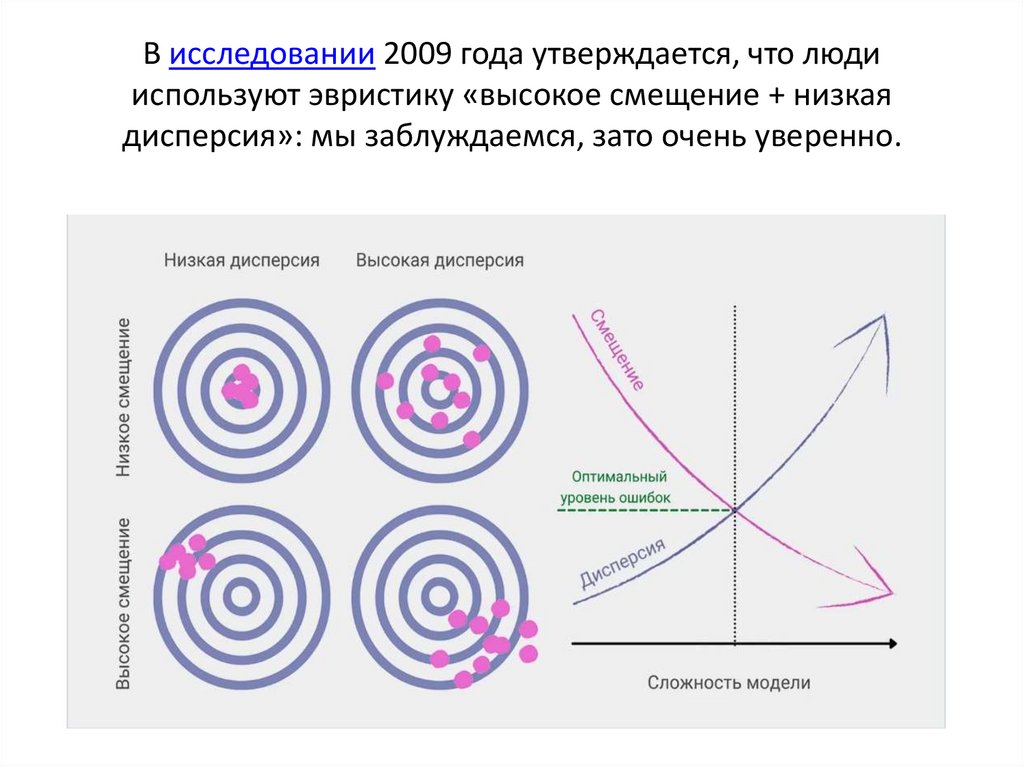
В исследовании 2009 года утверждается, что люди
используют эвристику «высокое смещение + низкая
дисперсия»: мы заблуждаемся, зато очень уверенно.

14.

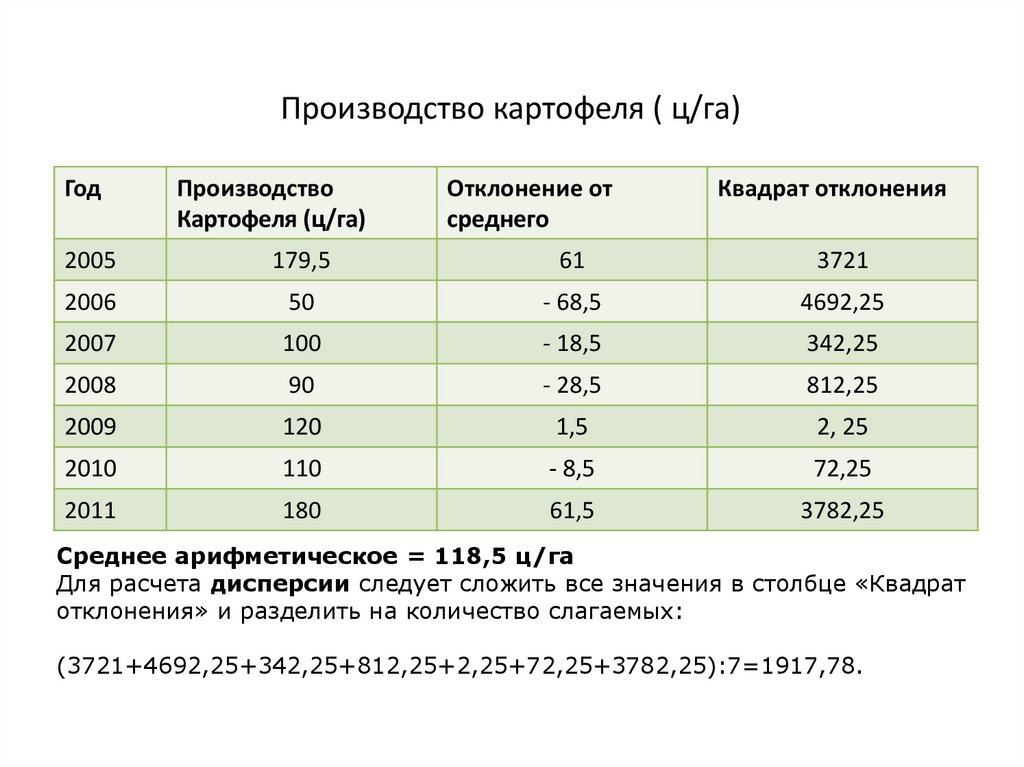
Производство картофеля ( ц/га)
Год
Производство
Картофеля (ц/га)
Отклонение от
среднего
Квадрат отклонения
2005
179,5
61
3721
2006
50
- 68,5
4692,25
2007
100
- 18,5
342,25
2008
90
- 28,5
812,25
2009
120
1,5
2, 25
2010
110
- 8,5
72,25
2011
180
61,5
3782,25
Среднее арифметическое = 118,5 ц/га
Для расчета дисперсии следует сложить все значения в столбце «Квадрат
отклонения» и разделить на количество слагаемых:
(3721+4692,25+342,25+812,25+2,25+72,25+3782,25):7=1917,78.