Similar presentations:
Пространственные фигуры (тетраэдр, куб, параллелепипед)
1.
3,а. ПРОСТРАНСТВЕННЫЕ ФИГУРЫ(Тетраэдр, куб, параллелепипед)
2.
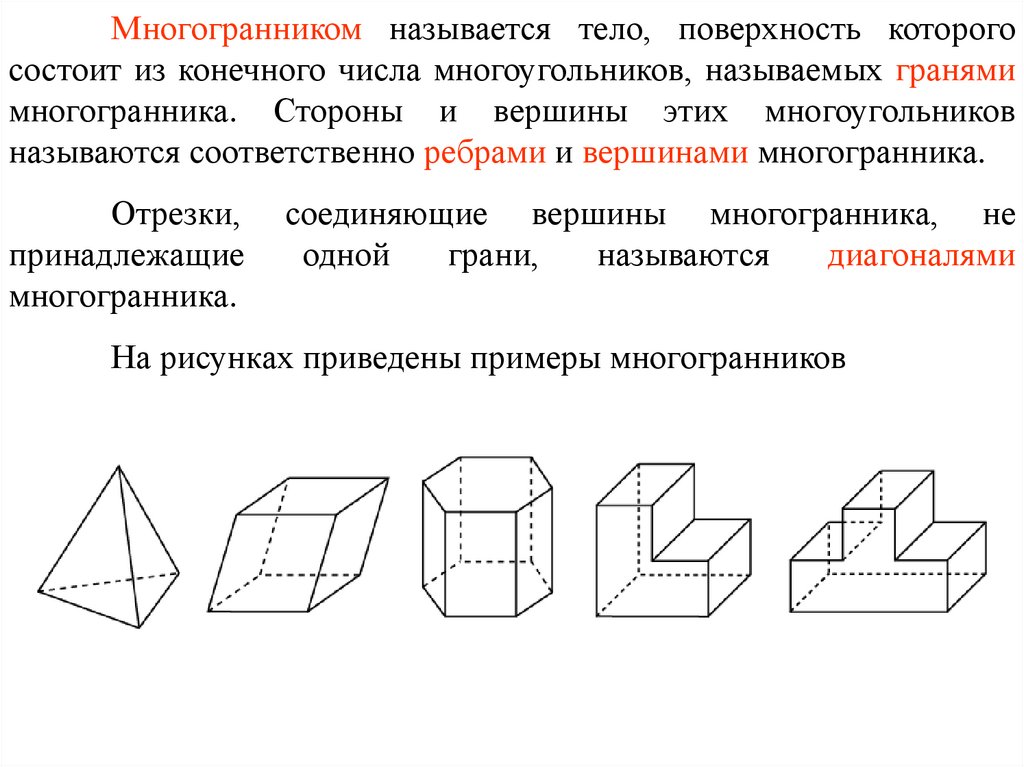
Многогранником называется тело, поверхность которогосостоит из конечного числа многоугольников, называемых гранями
многогранника. Стороны и вершины этих многоугольников
называются соответственно ребрами и вершинами многогранника.
Отрезки,
принадлежащие
многогранника.
соединяющие вершины многогранника, не
одной
грани,
называются
диагоналями
На рисунках приведены примеры многогранников
3.
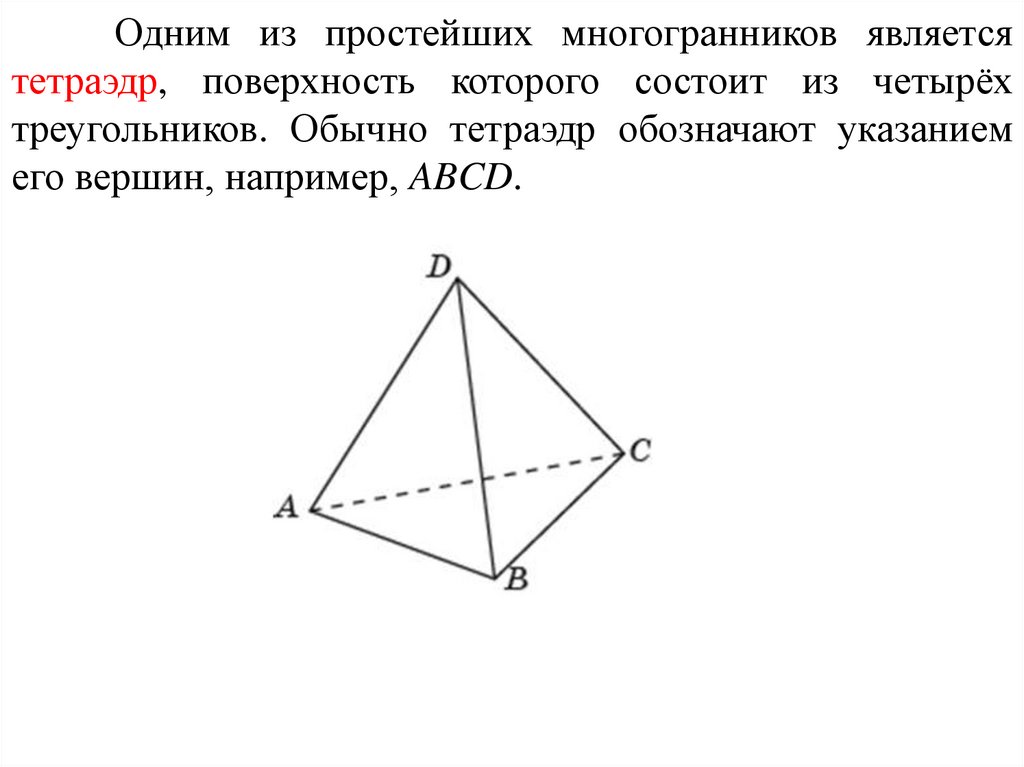
Одним из простейших многогранников являетсятетраэдр, поверхность которого состоит из четырёх
треугольников. Обычно тетраэдр обозначают указанием
его вершин, например, ABCD.
4.
УпражнениеНа клетчатой бумаге изобразите тетраэдр
аналогично данному на рисунке. Сколько у него
вершин (В), рёбер (Р) и граней (Г)?
Ответ: В = 4, Р = 6, Г = 4.
5.
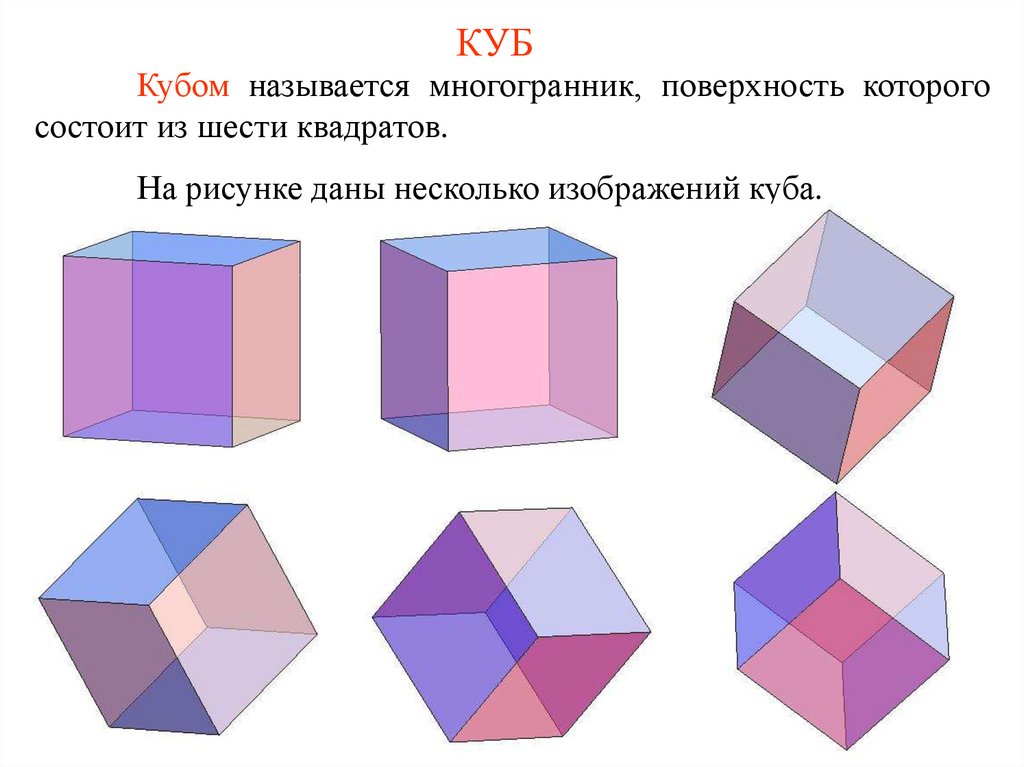
КУБКубом называется многогранник, поверхность которого
состоит из шести квадратов.
На рисунке даны несколько изображений куба.
6.
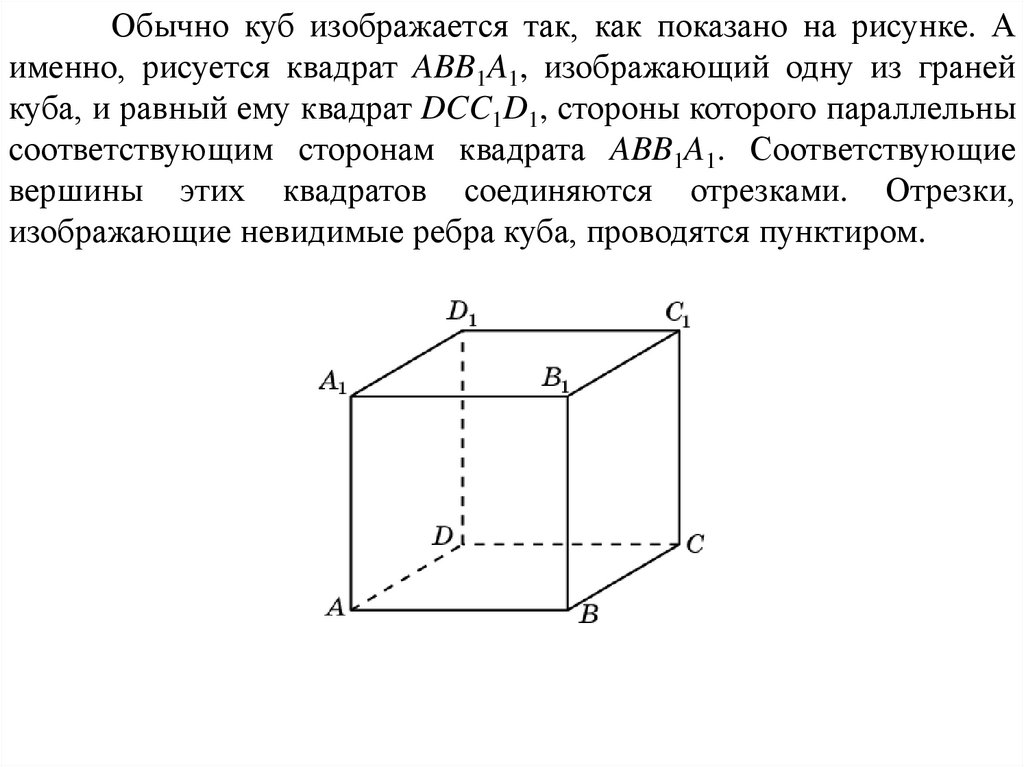
Обычно куб изображается так, как показано на рисунке. Аименно, рисуется квадрат ABB1A1, изображающий одну из граней
куба, и равный ему квадрат DCC1D1, стороны которого параллельны
соответствующим сторонам квадрата ABB1A1. Соответствующие
вершины этих квадратов соединяются отрезками. Отрезки,
изображающие невидимые ребра куба, проводятся пунктиром.
7.
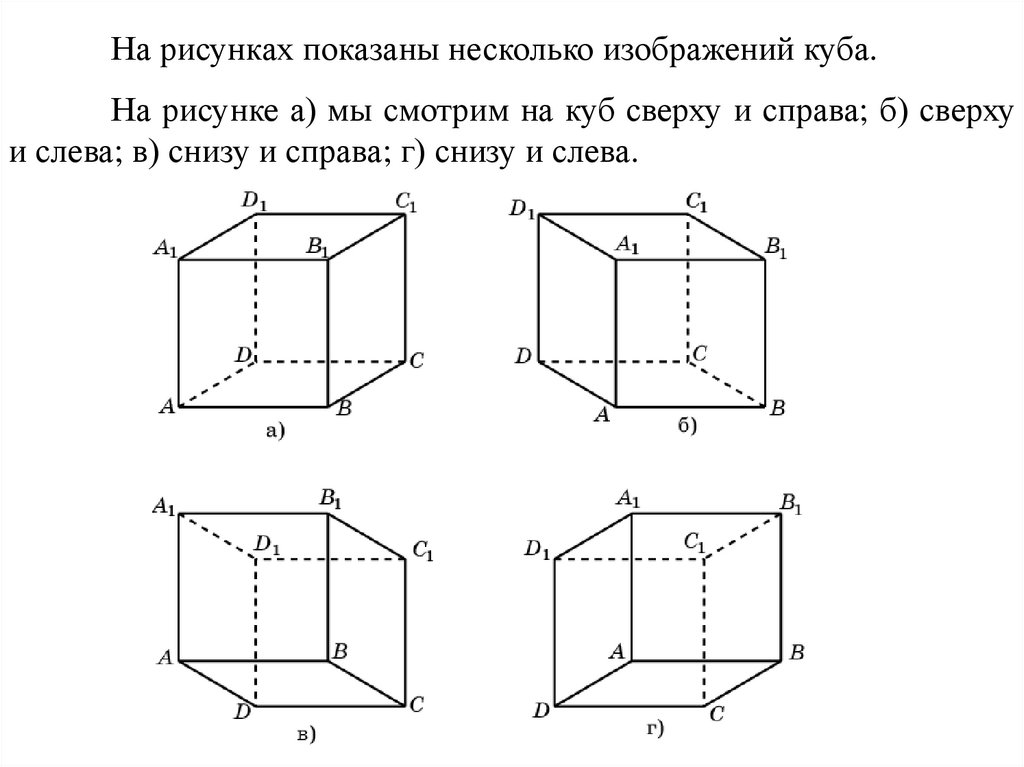
На рисунках показаны несколько изображений куба.На рисунке а) мы смотрим на куб сверху и справа; б) сверху
и слева; в) снизу и справа; г) снизу и слева.
8.
Упражнение 1Сколько вершин (В), рёбер (Р) и граней (Г) имеет куб?
Ответ: В = 8, Р = 12, Г = 6.
9.
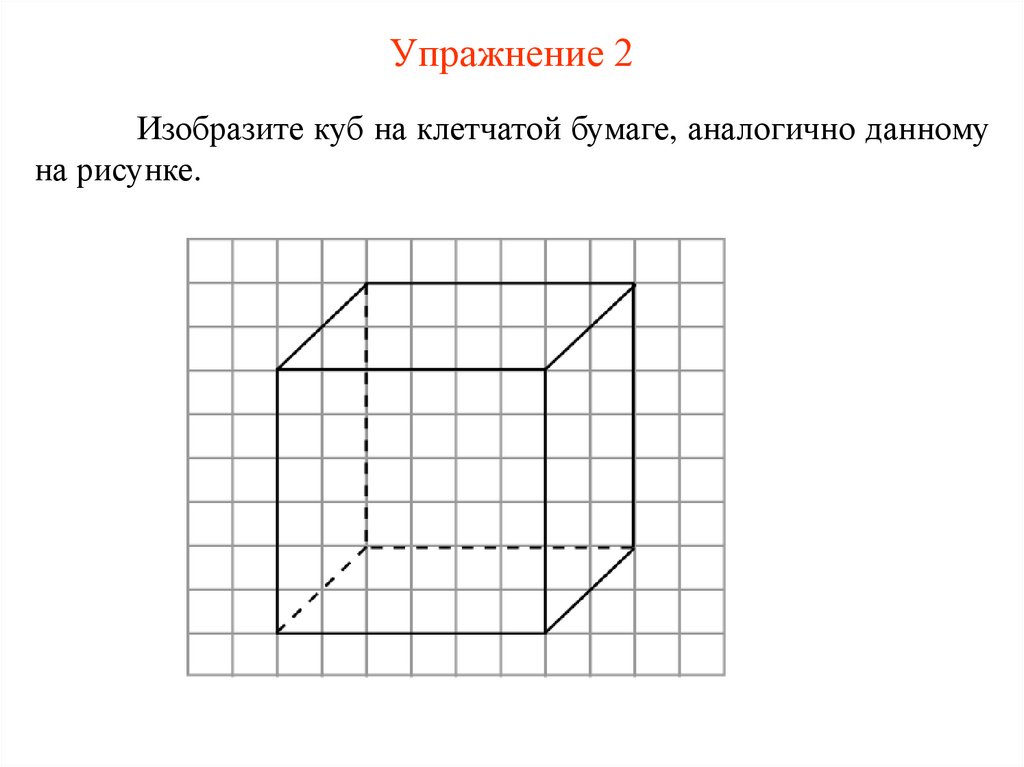
Упражнение 2Изобразите куб на клетчатой бумаге, аналогично данному
на рисунке.
10.
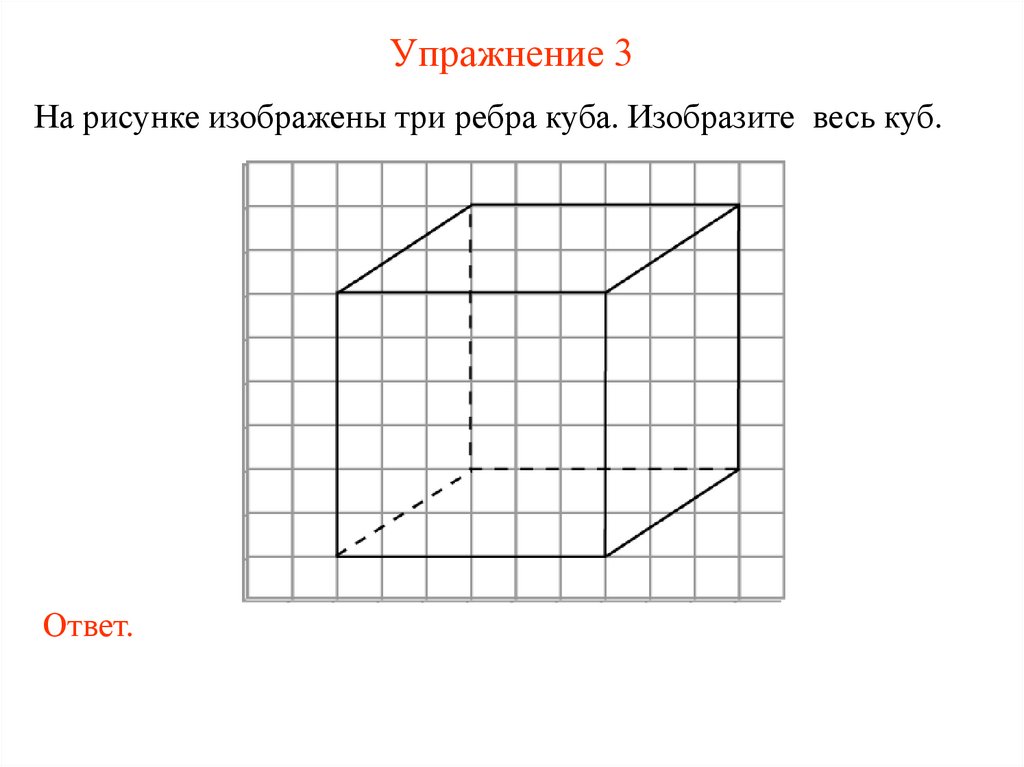
Упражнение 3На рисунке изображены три ребра куба. Изобразите весь куб.
Ответ.
11.
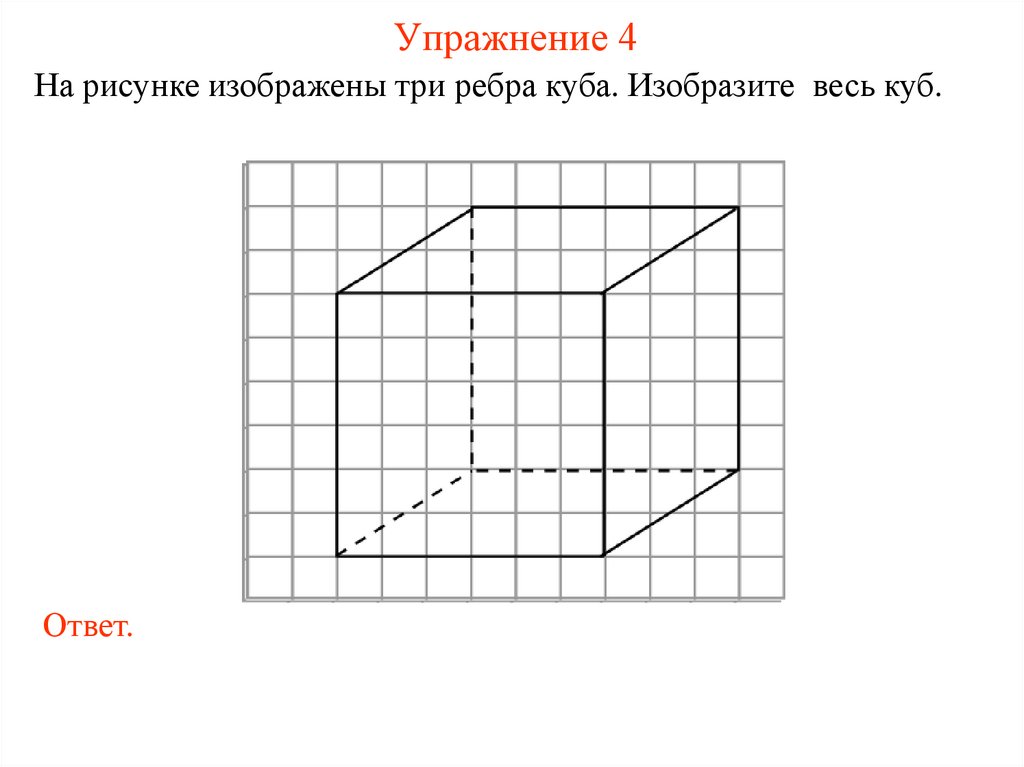
Упражнение 4На рисунке изображены три ребра куба. Изобразите весь куб.
Ответ.
12.
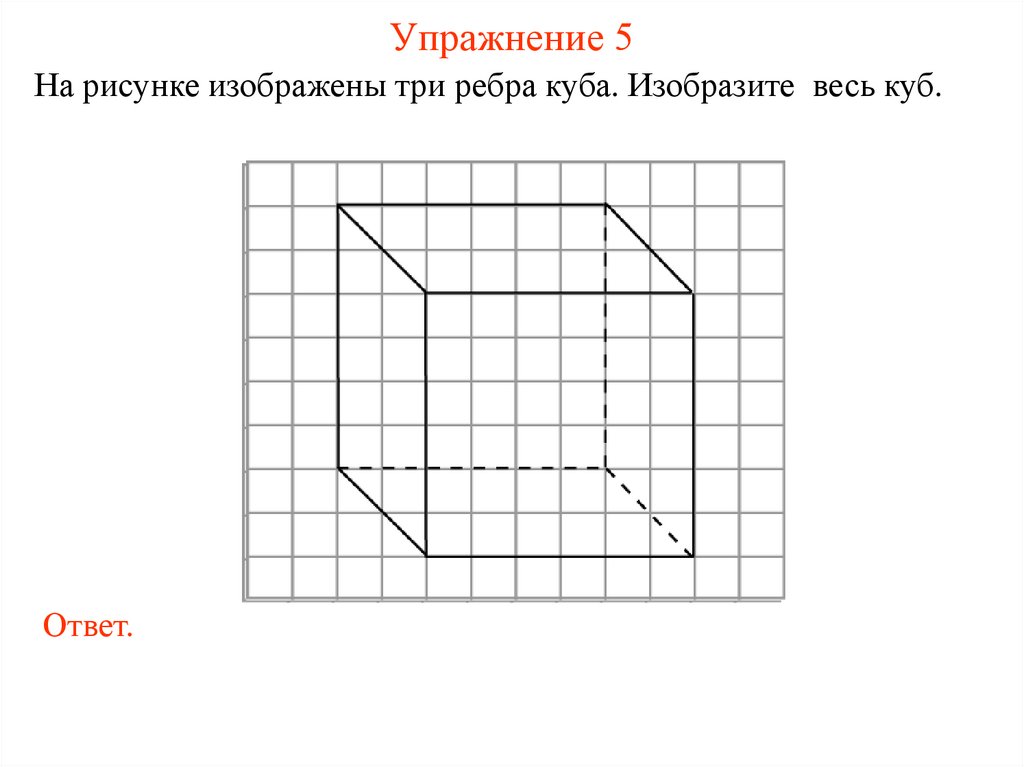
Упражнение 5На рисунке изображены три ребра куба. Изобразите весь куб.
Ответ.
13.
Упражнение 6На рисунке изображены три ребра куба. Изобразите весь куб.
Ответ.
14.
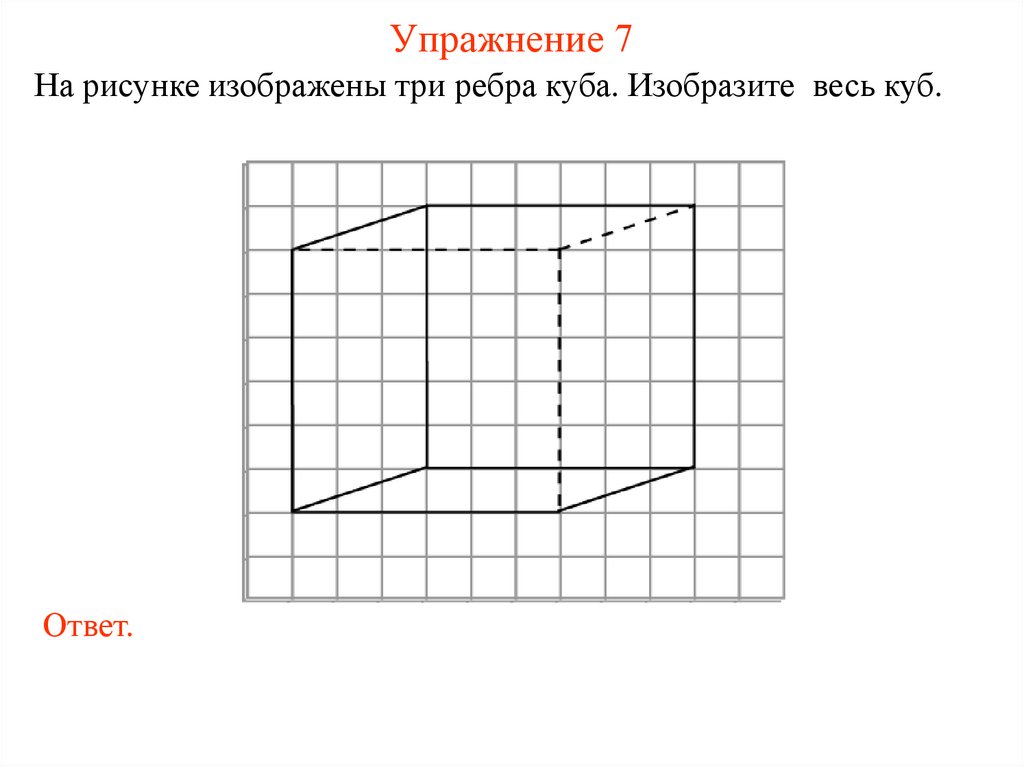
Упражнение 7На рисунке изображены три ребра куба. Изобразите весь куб.
Ответ.
15.
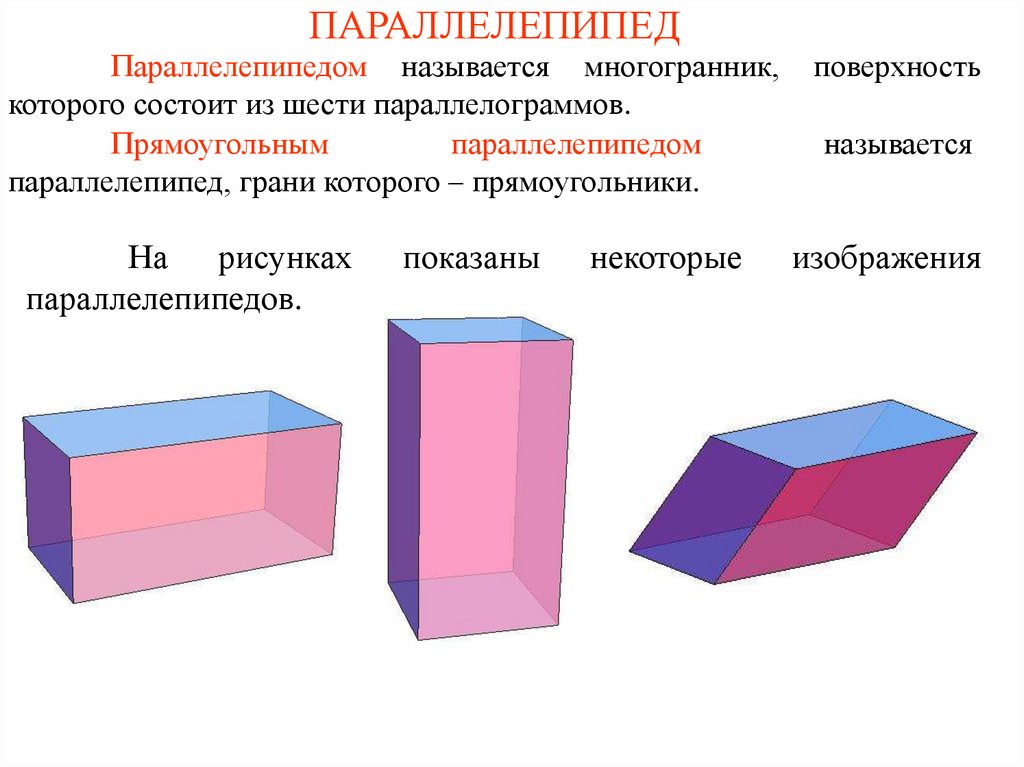
ПАРАЛЛЕЛЕПИПЕДПараллелепипедом называется многогранник,
которого состоит из шести параллелограммов.
Прямоугольным
параллелепипедом
параллелепипед, грани которого – прямоугольники.
поверхность
На рисунках
параллелепипедов.
изображения
показаны
некоторые
называется
16.
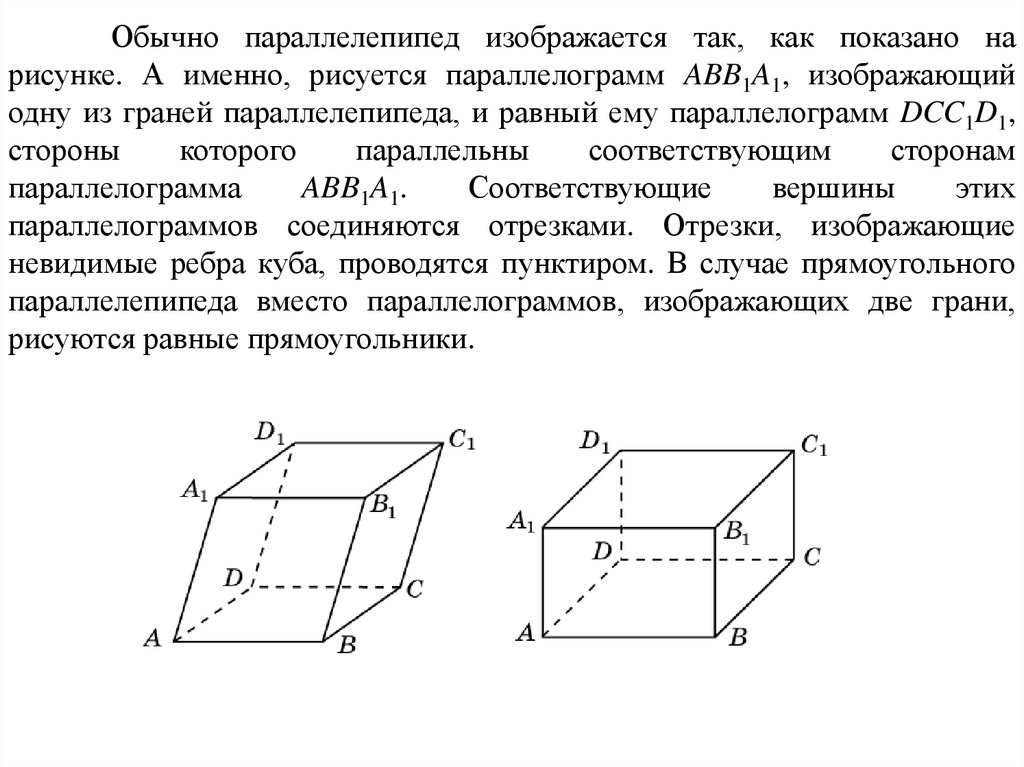
Обычно параллелепипед изображается так, как показано нарисунке. А именно, рисуется параллелограмм ABB1A1, изображающий
одну из граней параллелепипеда, и равный ему параллелограмм DCC1D1,
стороны
которого
параллельны
соответствующим
сторонам
параллелограмма
ABB1A1.
Соответствующие
вершины
этих
параллелограммов соединяются отрезками. Отрезки, изображающие
невидимые ребра куба, проводятся пунктиром. В случае прямоугольного
параллелепипеда вместо параллелограммов, изображающих две грани,
рисуются равные прямоугольники.
17.
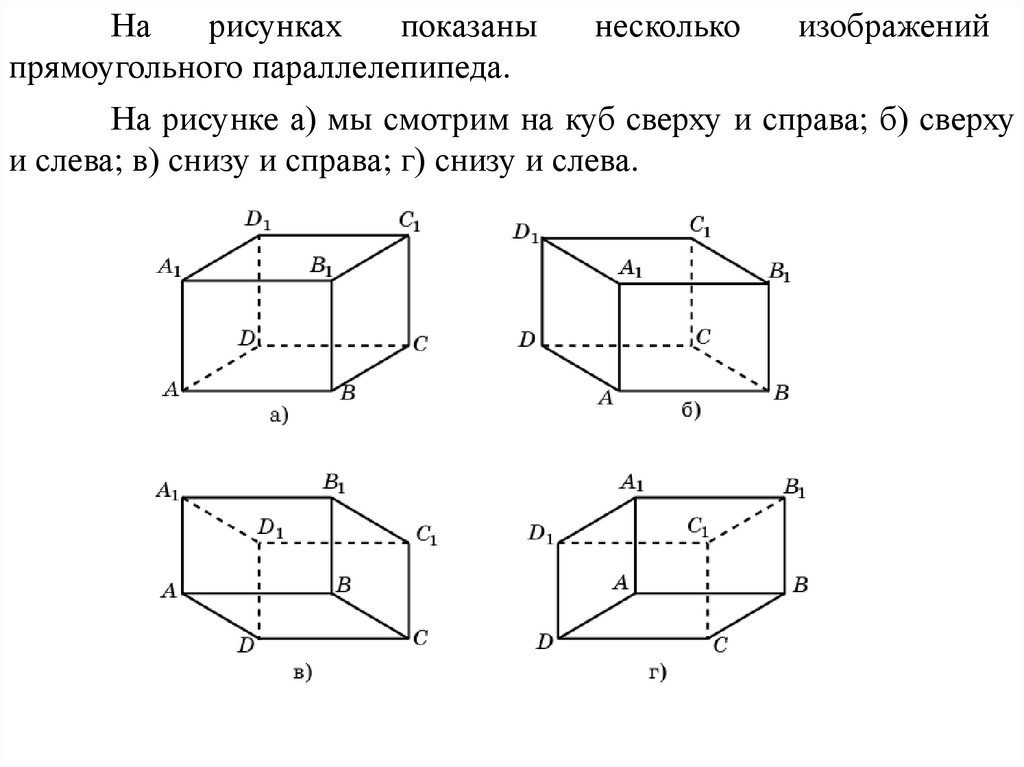
Нарисунках
показаны
прямоугольного параллелепипеда.
несколько
изображений
На рисунке а) мы смотрим на куб сверху и справа; б) сверху
и слева; в) снизу и справа; г) снизу и слева.
18.
Упражнение 1Сколько вершин (В), рёбер (Р) и граней (Г) имеет
параллелепипед?
Ответ: В = 8, Р = 12, Г = 6.
19.
Упражнение 2Изобразите прямоугольный параллелепипед на клетчатой
бумаге, аналогично данному на рисунке.
20.
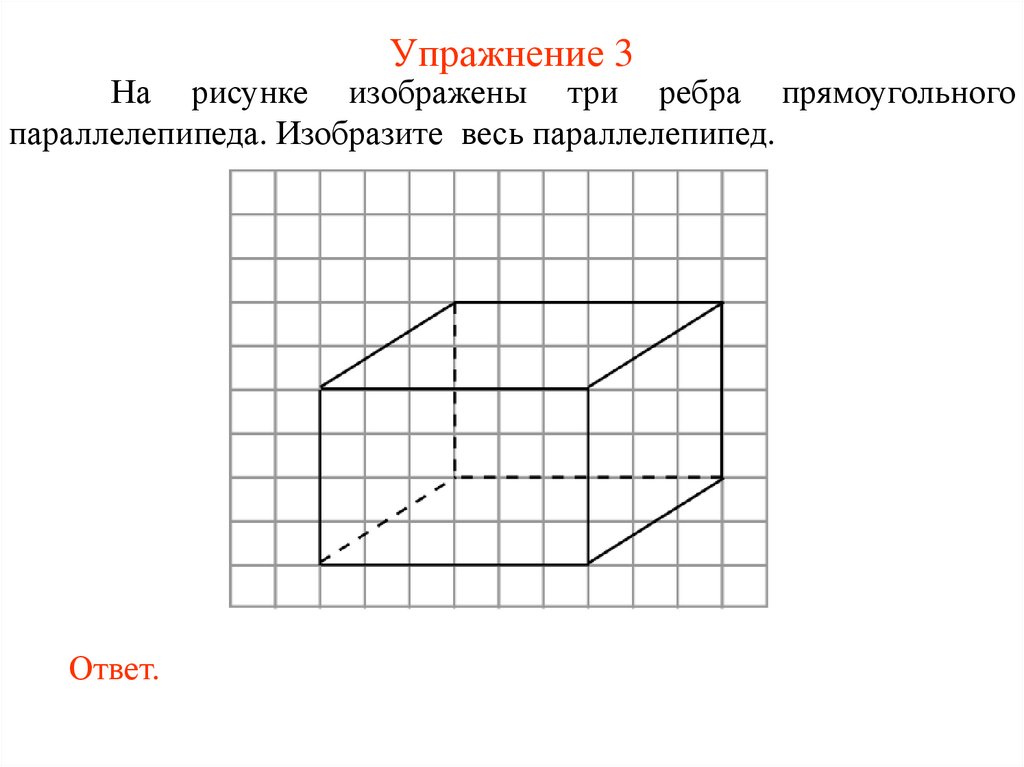
Упражнение 3На рисунке изображены три ребра прямоугольного
параллелепипеда. Изобразите весь параллелепипед.
Ответ.
21.
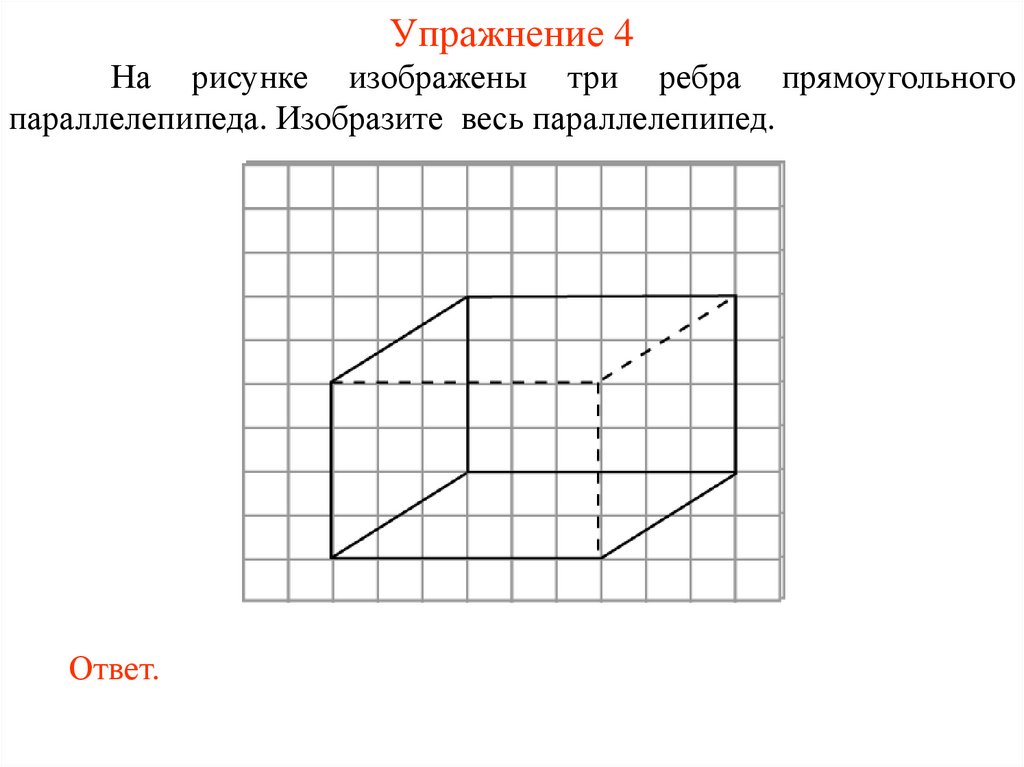
Упражнение 4На рисунке изображены три ребра прямоугольного
параллелепипеда. Изобразите весь параллелепипед.
Ответ.
22.
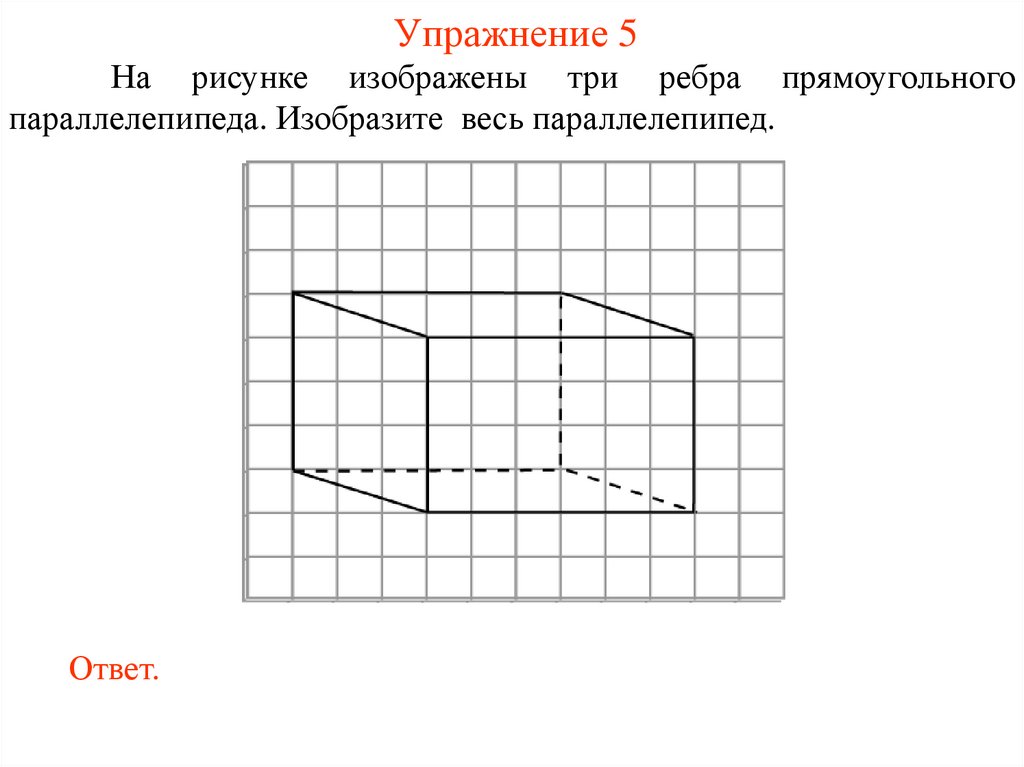
Упражнение 5На рисунке изображены три ребра прямоугольного
параллелепипеда. Изобразите весь параллелепипед.
Ответ.
23.
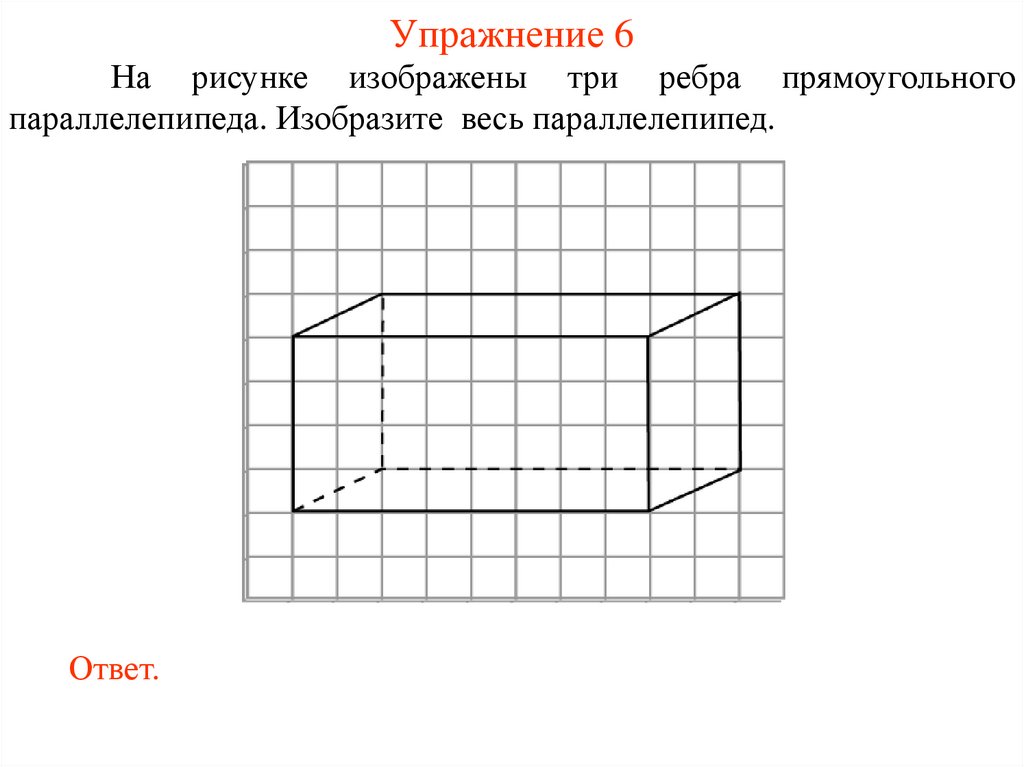
Упражнение 6На рисунке изображены три ребра прямоугольного
параллелепипеда. Изобразите весь параллелепипед.
Ответ.
24.
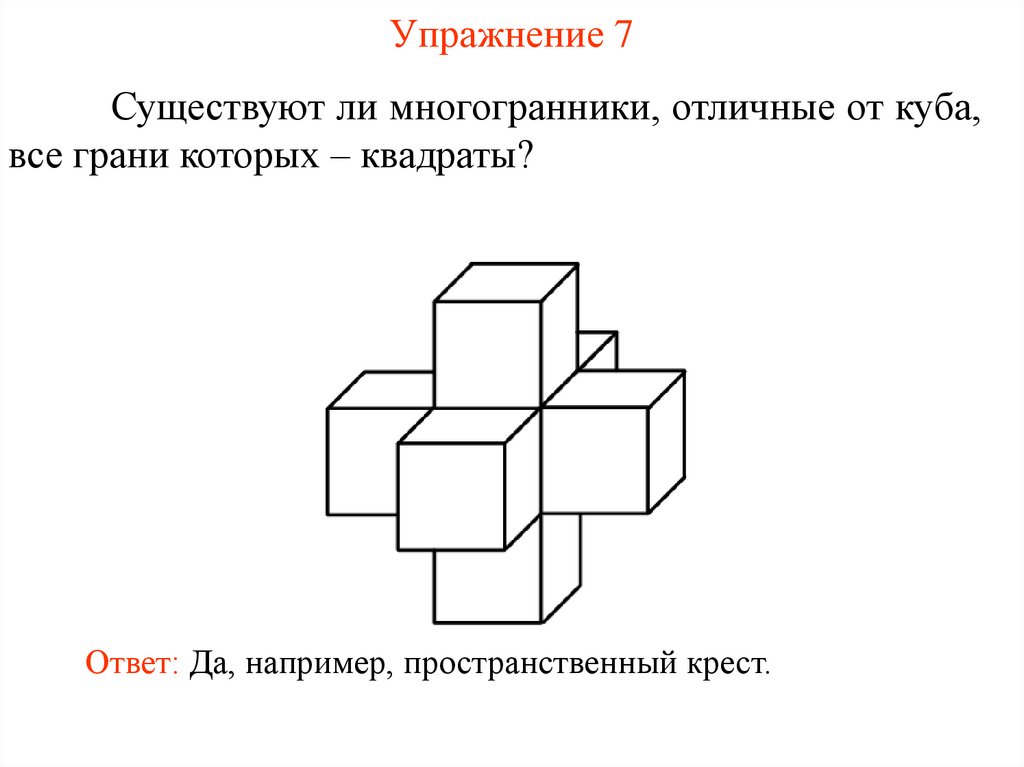
Упражнение 7Существуют ли многогранники, отличные от куба,
все грани которых – квадраты?
Ответ: Да, например, пространственный крест.
25.
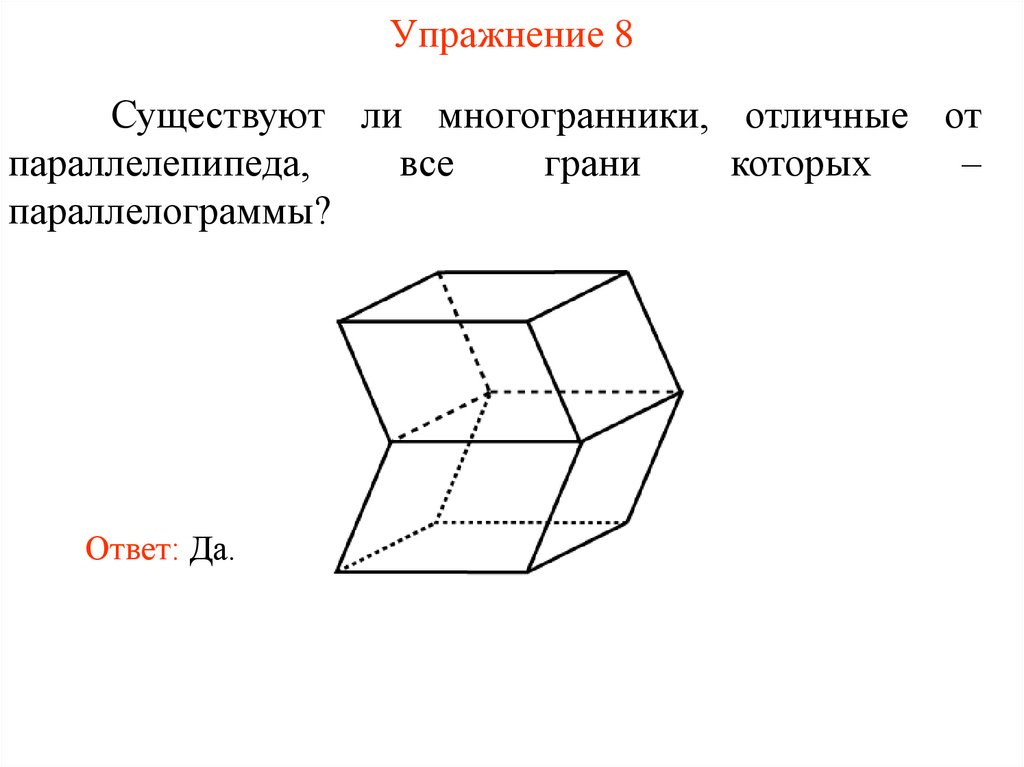
Упражнение 8Существуют ли многогранники, отличные от
параллелепипеда,
все
грани
которых
–
параллелограммы?
Ответ: Да.
26.
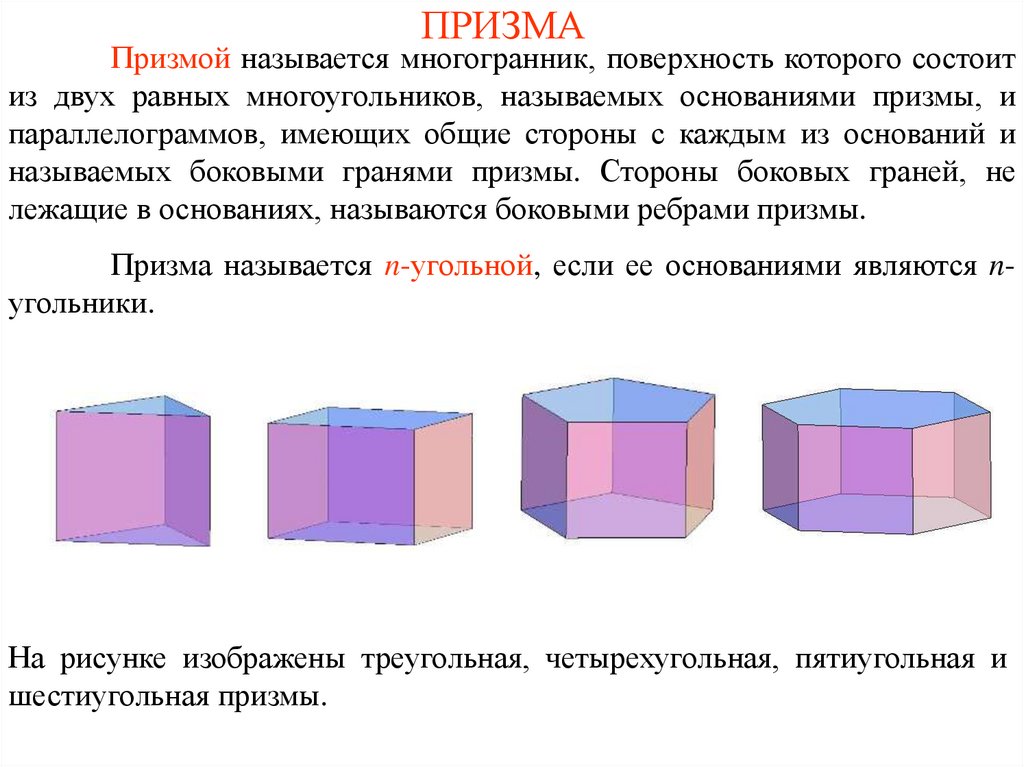
ПРИЗМАПризмой называется многогранник, поверхность которого состоит
из двух равных многоугольников, называемых основаниями призмы, и
параллелограммов, имеющих общие стороны с каждым из оснований и
называемых боковыми гранями призмы. Стороны боковых граней, не
лежащие в основаниях, называются боковыми ребрами призмы.
Призма называется n-угольной, если ее основаниями являются nугольники.
На рисунке изображены треугольная, четырехугольная, пятиугольная и
шестиугольная призмы.
27.
Призма называется прямой, если её боковые грани –прямоугольники.
На рисунке изображена прямая треугольная призма, ABB1A1
– прямоугольник.
28.
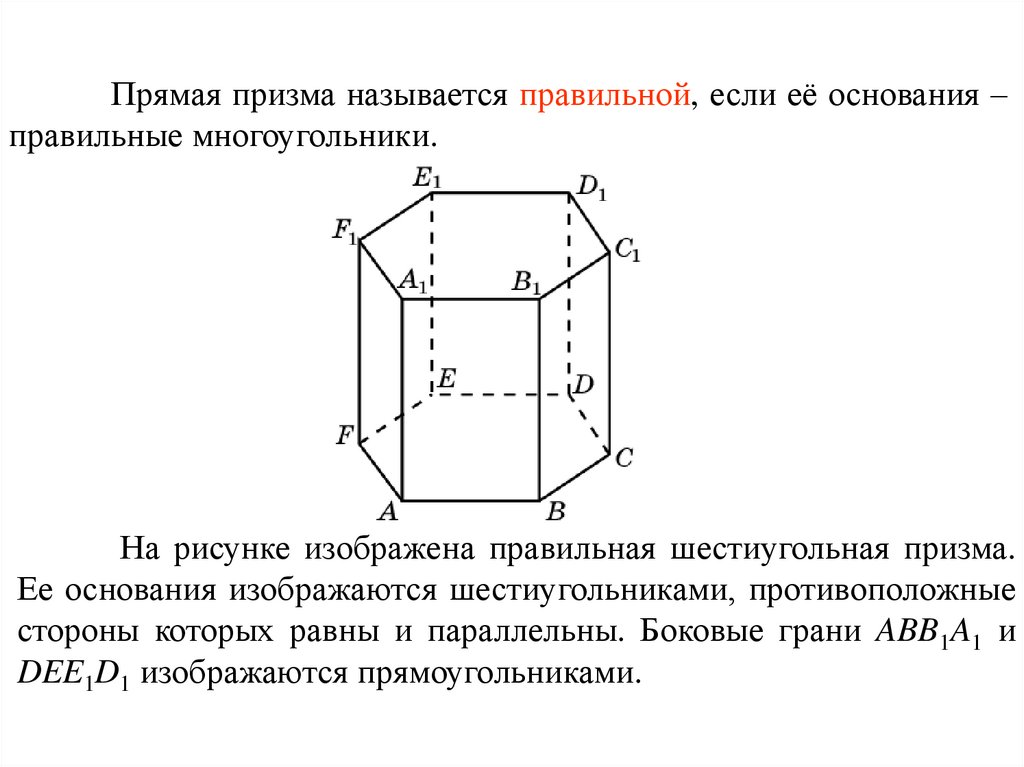
Прямая призма называется правильной, если её основания –правильные многоугольники.
На рисунке изображена правильная шестиугольная призма.
Ее основания изображаются шестиугольниками, противоположные
стороны которых равны и параллельны. Боковые грани ABB1A1 и
DEE1D1 изображаются прямоугольниками.
29.
Упражнение 1Сколько вершин (В), рёбер (Р) и граней (Г) имеет nугольная призма?
Ответ: В = 2n, Р = 3n, Г = n + 2.
30.
Упражнение 2Существует ли призма, которая имеет:
а) 4 ребра?
Ответ: Нет.
б) 6 рёбер?
в) 12 рёбер?
Ответ: Нет.
Ответ: Да.
г) 21 ребро?
Ответ: Да.
31.
Упражнение 3Какой многоугольник лежит в основании призмы,
которая имеет:
а) 18 рёбер?
Ответ: Шестиугольник.
б) 24 вершины?
Ответ: Двенадцатиугольник.
в) 36 граней?
Ответ: Тридцатичетырёхугольник.
32.
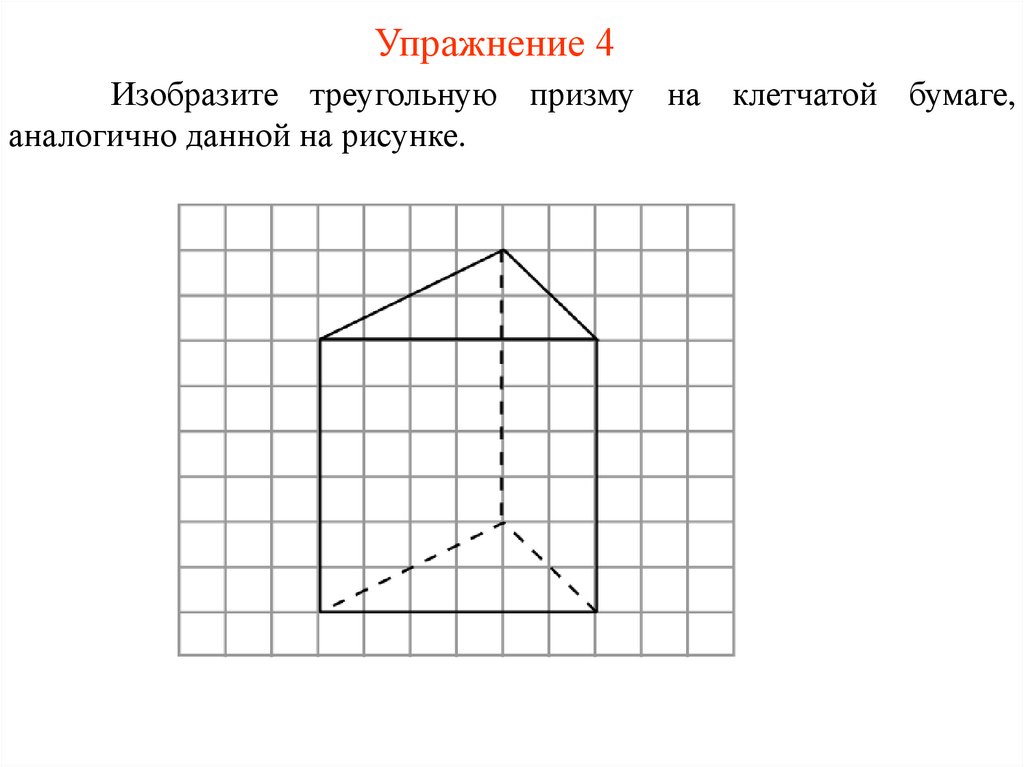
Упражнение 4Изобразите треугольную призму на клетчатой бумаге,
аналогично данной на рисунке.
33.
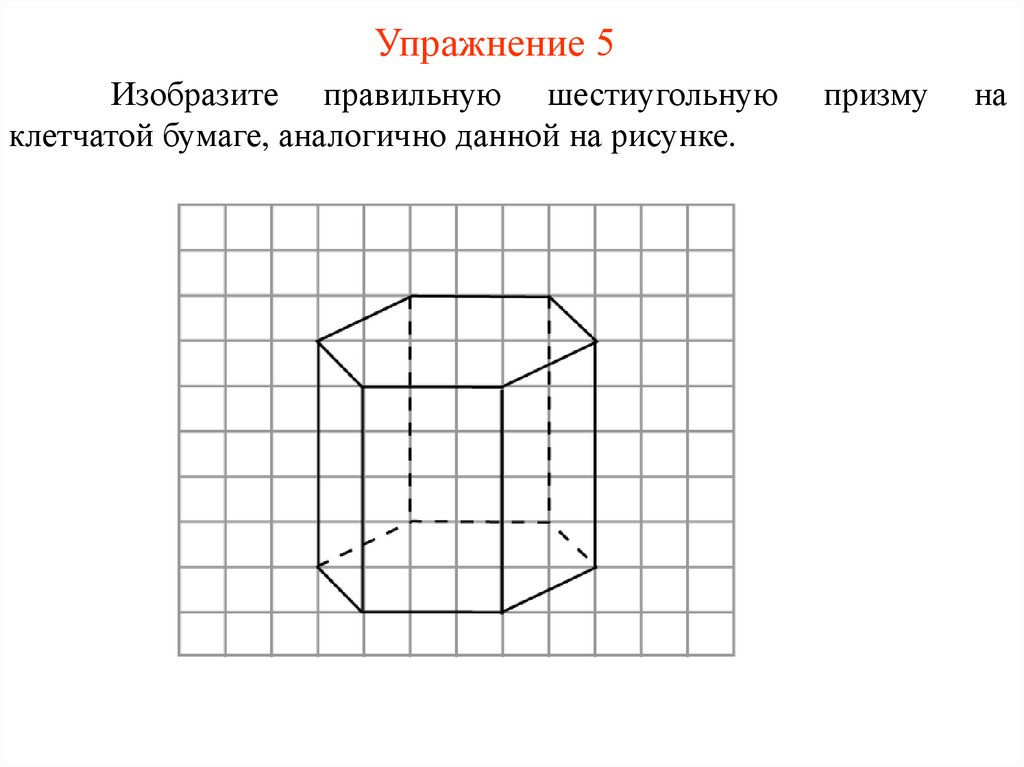
Упражнение 5Изобразите правильную шестиугольную
клетчатой бумаге, аналогично данной на рисунке.
призму
на
34.
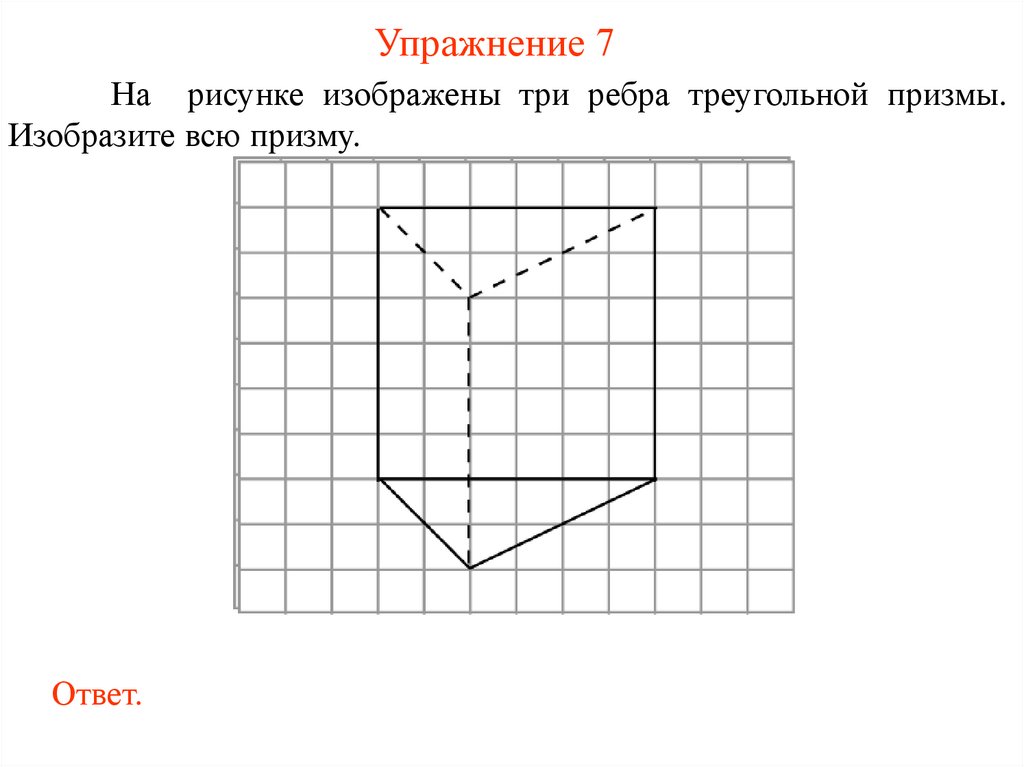
Упражнение 7На рисунке изображены три ребра треугольной призмы.
Изобразите всю призму.
Ответ.
35.
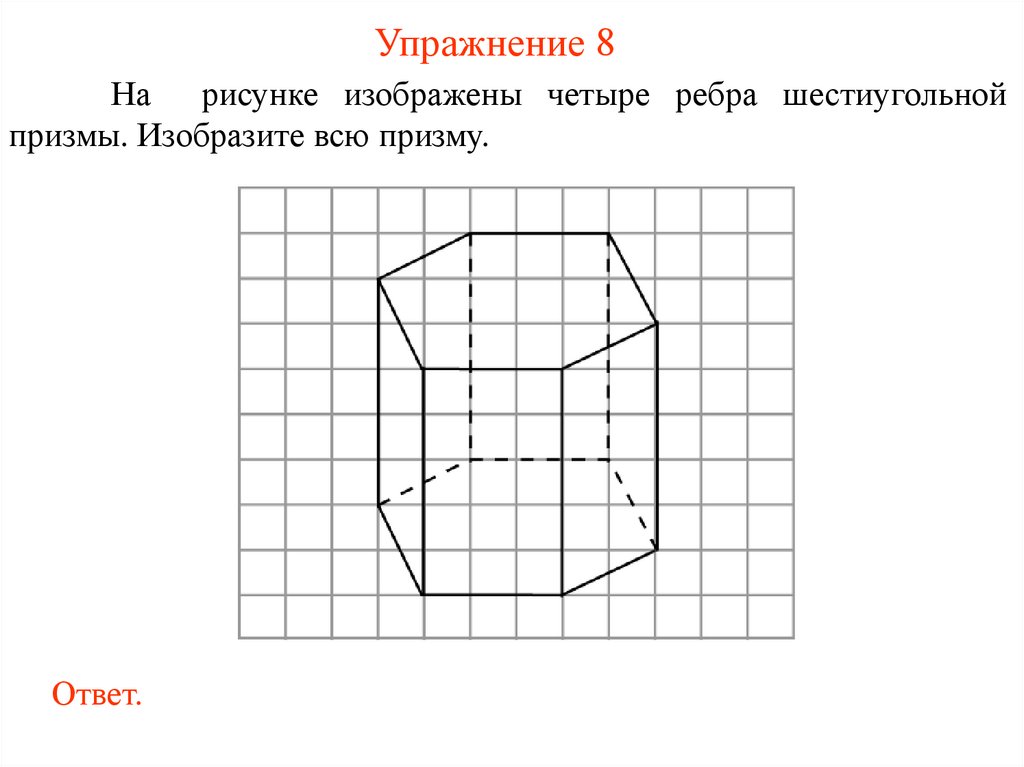
Упражнение 8На рисунке изображены четыре ребра шестиугольной
призмы. Изобразите всю призму.
Ответ.
36.
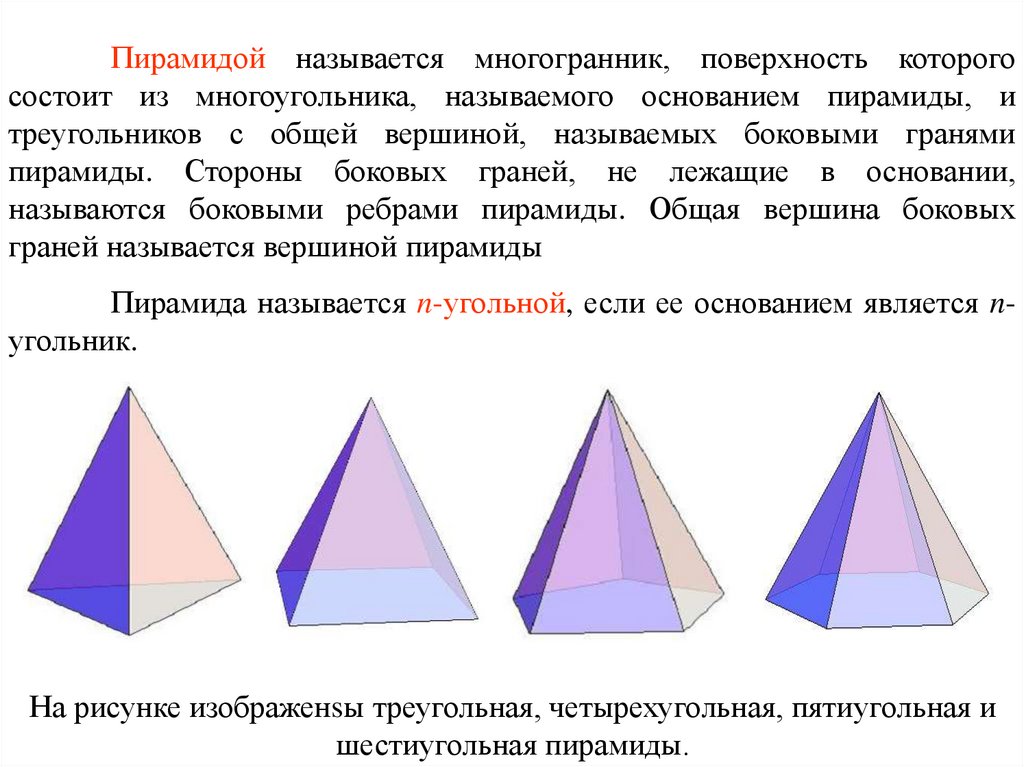
Пирамидой называется многогранник, поверхность которогосостоит из многоугольника, называемого основанием пирамиды, и
треугольников с общей вершиной, называемых боковыми гранями
пирамиды. Стороны боковых граней, не лежащие в основании,
называются боковыми ребрами пирамиды. Общая вершина боковых
граней называется вершиной пирамиды
Пирамида называется n-угольной, если ее основанием является nугольник.
На рисунке изображенsы треугольная, четырехугольная, пятиугольная и
шестиугольная пирамиды.
37.
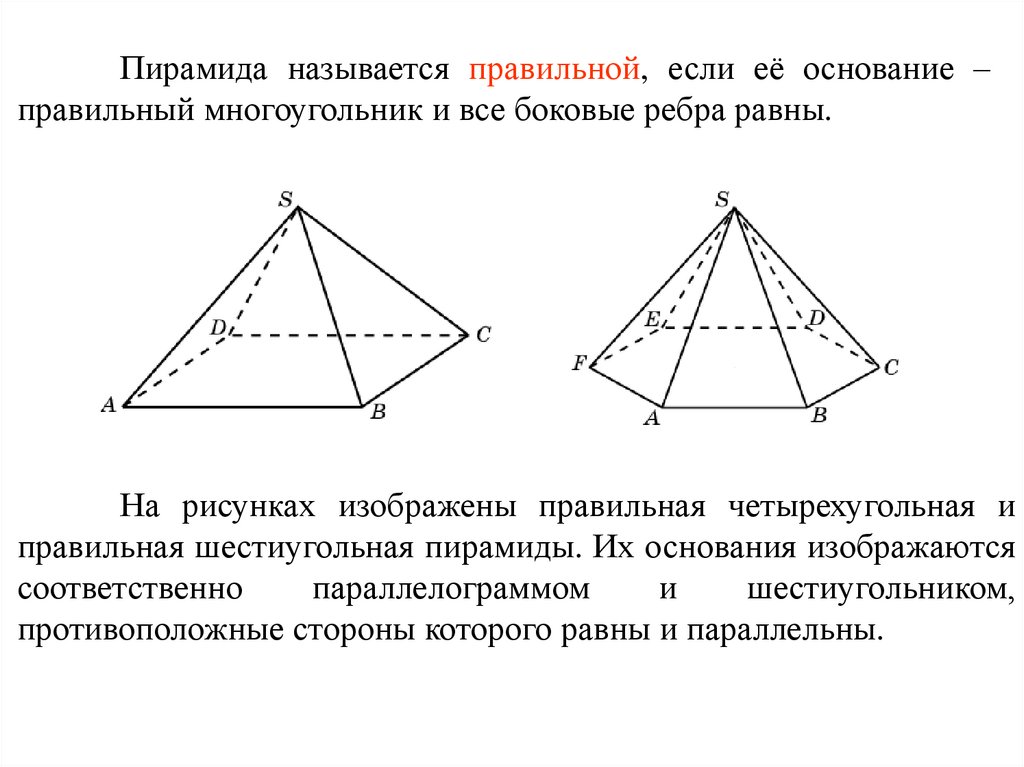
Пирамида называется правильной, если её основание –правильный многоугольник и все боковые ребра равны.
На рисунках изображены правильная четырехугольная и
правильная шестиугольная пирамиды. Их основания изображаются
соответственно
параллелограммом
и
шестиугольником,
противоположные стороны которого равны и параллельны.
38.
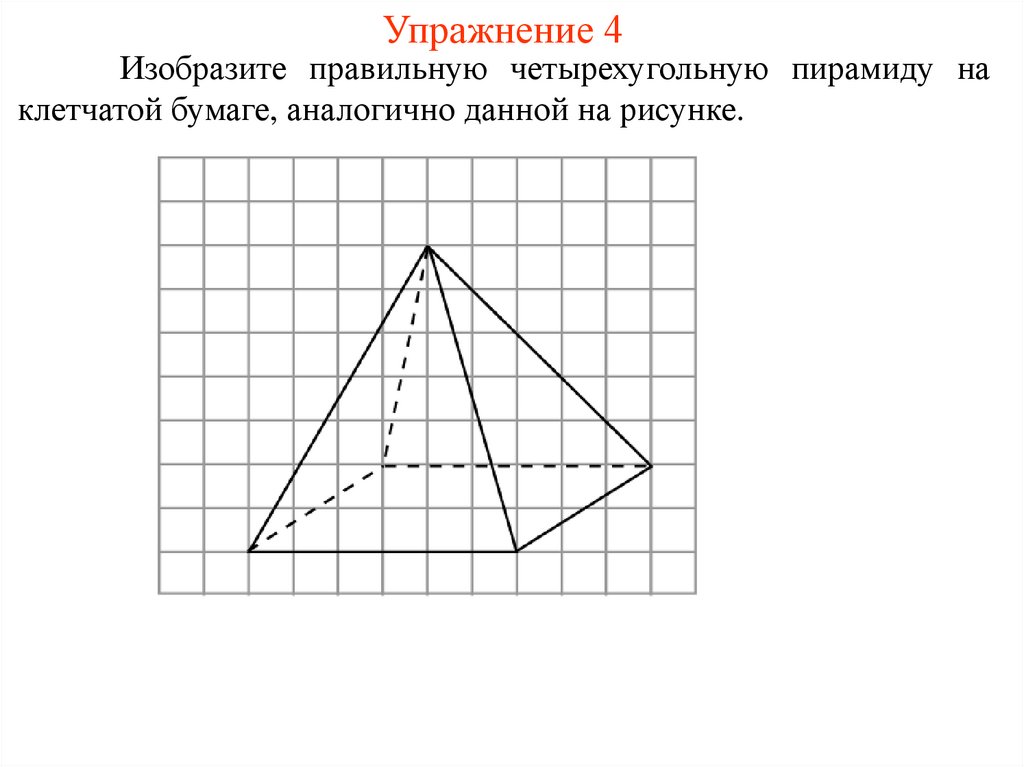
Упражнение 4Изобразите правильную четырехугольную пирамиду на
клетчатой бумаге, аналогично данной на рисунке.
39.
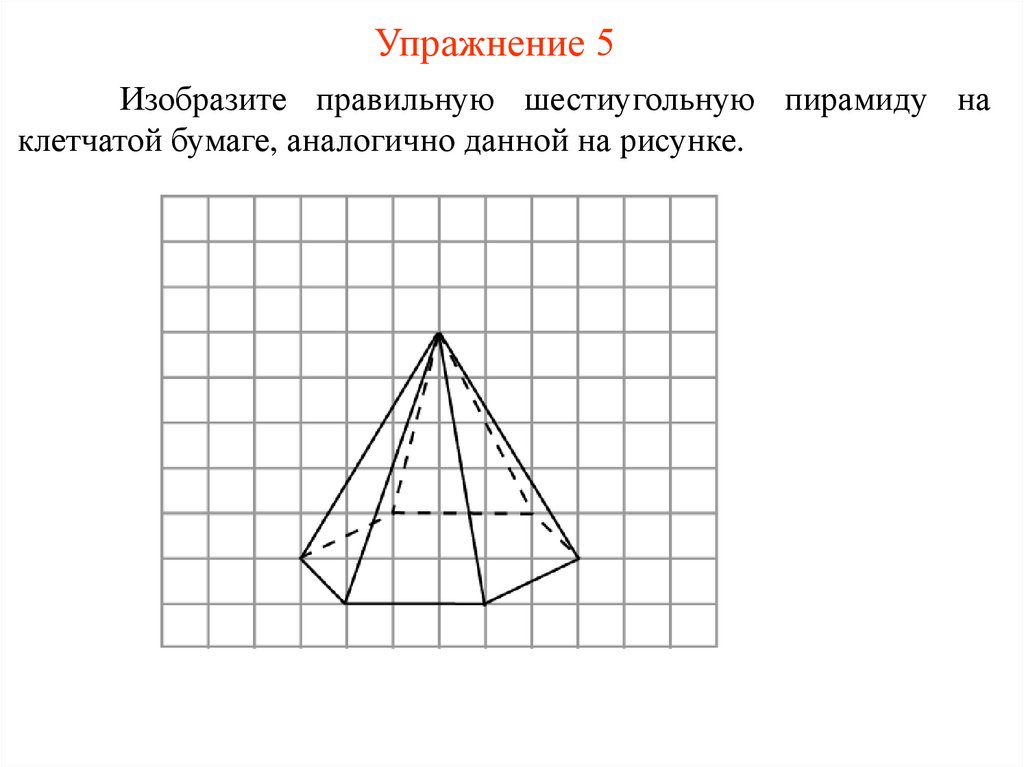
Упражнение 5Изобразите правильную шестиугольную пирамиду на
клетчатой бумаге, аналогично данной на рисунке.
40.
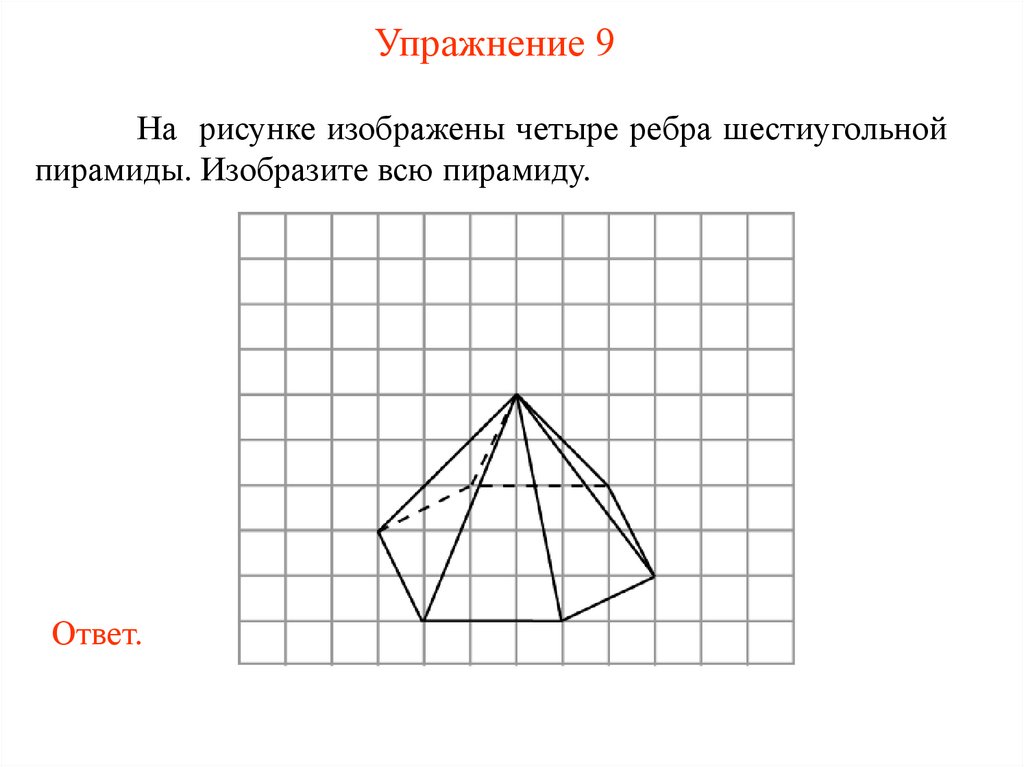
Упражнение 9На рисунке изображены четыре ребра шестиугольной
пирамиды. Изобразите всю пирамиду.
Ответ.
41.
Упражнение 1Сколько вершин (В), рёбер (Р) и граней (Г) имеет nугольная пирамида?
Ответ: В = n + 1, Р = 2n, Г = n + 1.
42.
Упражнение 2Существует ли пирамида, которая имеет:
а) 10 ребер?
Ответ: Да.
б) 6 рёбер?
Ответ: Да.
в) 24 ребра?
г) 33 ребра?
Ответ: Да.
Ответ: Нет.
43.
Упражнение 3Какой многоугольник лежит в основании пирамиды,
которая имеет:
а) 8 рёбер?
Ответ: 4-угольник.
б) 22 вершины?
Ответ: 21-угольник.
в) 60 граней?
Ответ: 59-угольник.













 mathematics
mathematics








