Similar presentations:
Пространственные фигуры (Призма)
1.
Работа в классе2.
3,б. ПРОСТРАНСТВЕННЫЕ ФИГУРЫ(Призма)
3.
ПРИЗМАПризмой называется многогранник, поверхность которого состоит
из двух равных многоугольников, называемых основаниями призмы, и
параллелограммов, имеющих общие стороны с каждым из оснований и
называемых боковыми гранями призмы. Стороны боковых граней, не
лежащие в основаниях, называются боковыми ребрами призмы.
Призма называется n-угольной, если ее основаниями являются nугольники.
На рисунке изображены треугольная, четырехугольная, пятиугольная и
шестиугольная призмы.
4.
Призма называется прямой, если её боковые грани –прямоугольники.
На рисунке изображена прямая треугольная призма, ABB1A1
– прямоугольник.
5.
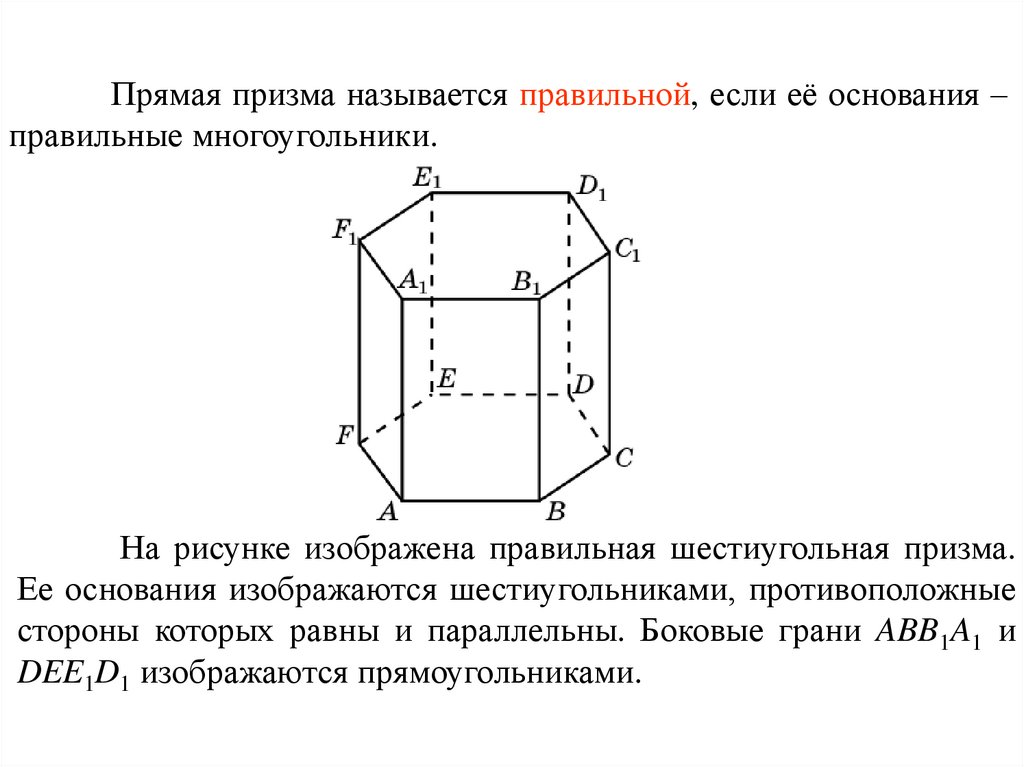
Прямая призма называется правильной, если её основания –правильные многоугольники.
На рисунке изображена правильная шестиугольная призма.
Ее основания изображаются шестиугольниками, противоположные
стороны которых равны и параллельны. Боковые грани ABB1A1 и
DEE1D1 изображаются прямоугольниками.
6.
Упражнение 1Сколько вершин (В), рёбер (Р) и граней (Г) имеет nугольная призма?
Ответ: В = 2n, Р = 3n, Г = n + 2.
7.
Упражнение 2Существует ли призма, которая имеет:
а) 4 ребра?
Ответ: Нет.
б) 6 рёбер?
в) 12 рёбер?
Ответ: Нет.
Ответ: Да.
г) 21 ребро?
Ответ: Да.
8.
Упражнение 3Какой многоугольник лежит в основании призмы,
которая имеет:
а) 18 рёбер?
Ответ: Шестиугольник.
б) 24 вершины?
Ответ: Двенадцатиугольник.
в) 36 граней?
Ответ: Тридцатичетырёхугольник.
9.
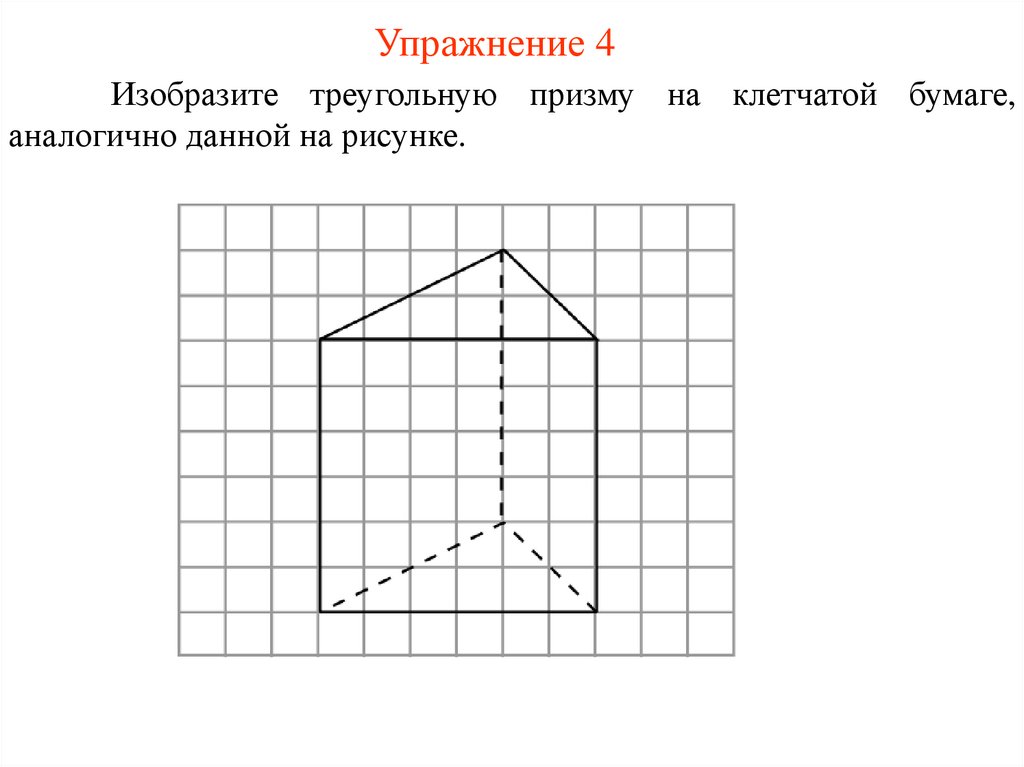
Упражнение 4Изобразите треугольную призму на клетчатой бумаге,
аналогично данной на рисунке.
10.
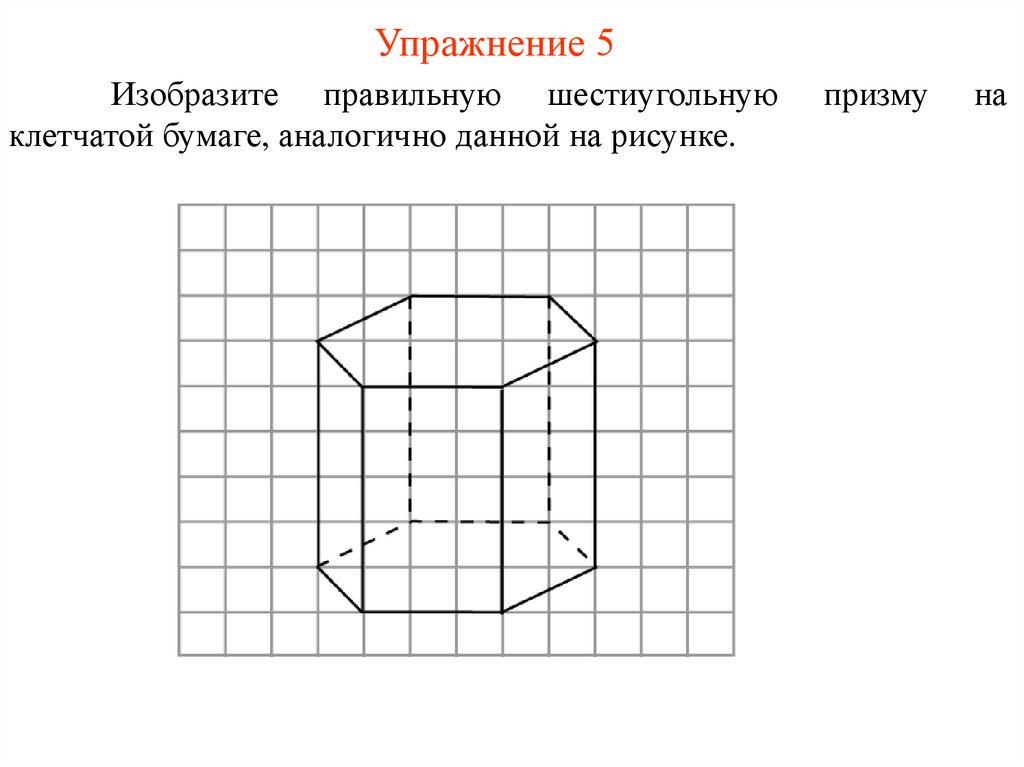
Упражнение 5Изобразите правильную шестиугольную
клетчатой бумаге, аналогично данной на рисунке.
призму
на
11.
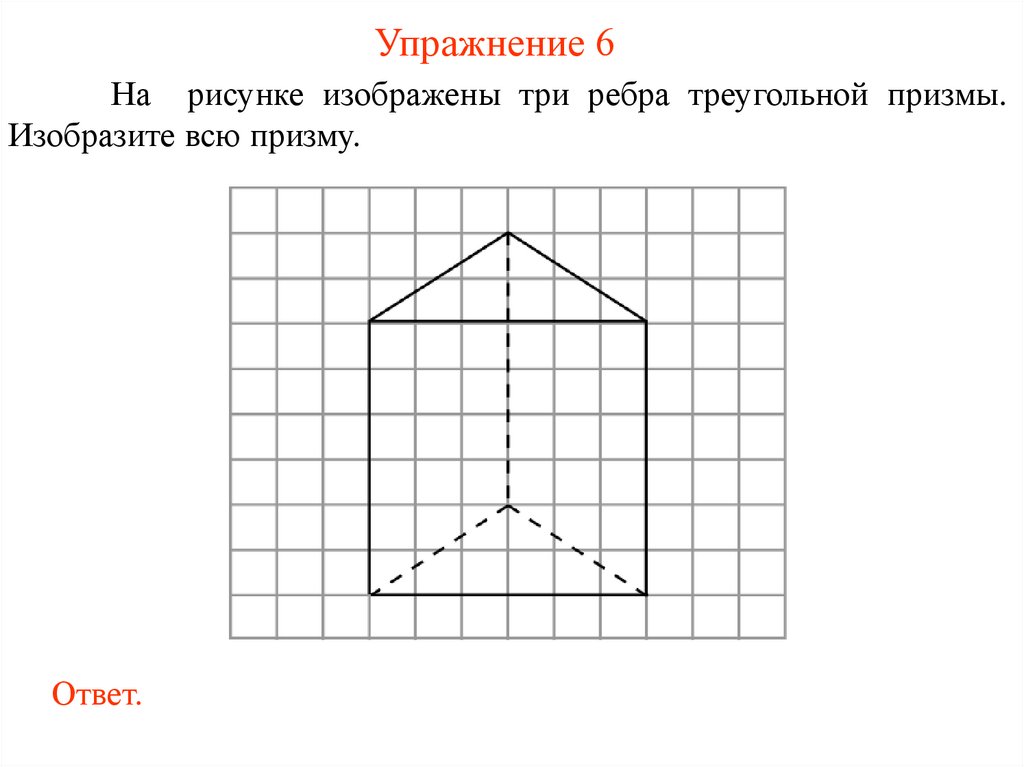
Упражнение 6На рисунке изображены три ребра треугольной призмы.
Изобразите всю призму.
Ответ.
12.
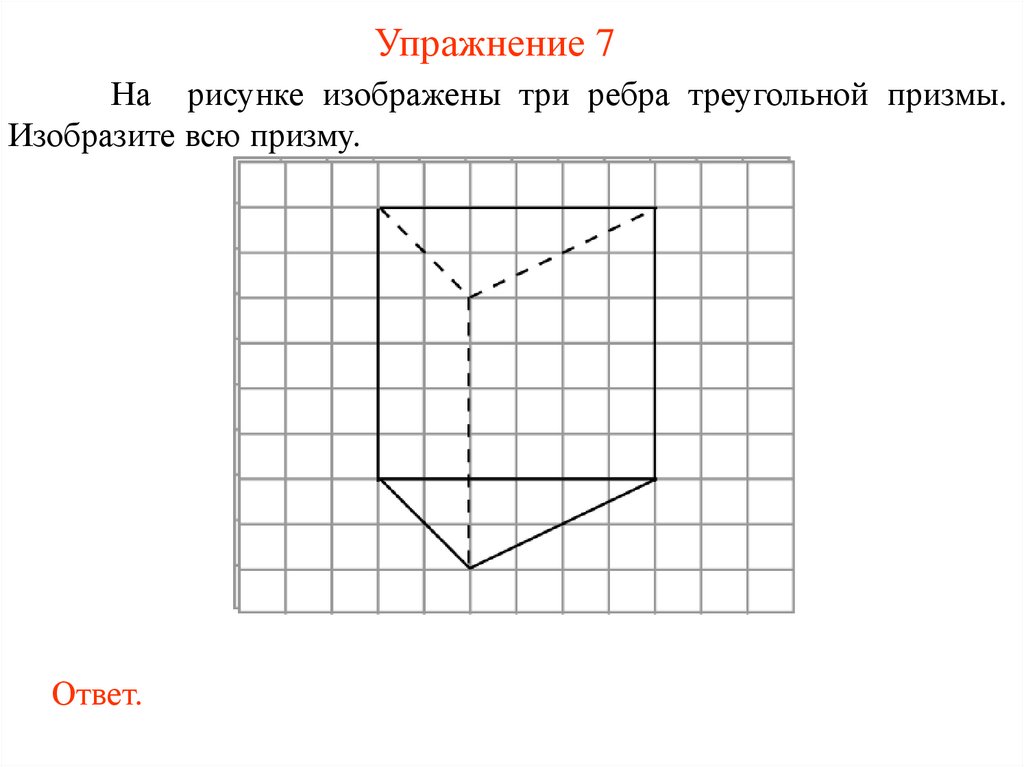
Упражнение 7На рисунке изображены три ребра треугольной призмы.
Изобразите всю призму.
Ответ.
13.
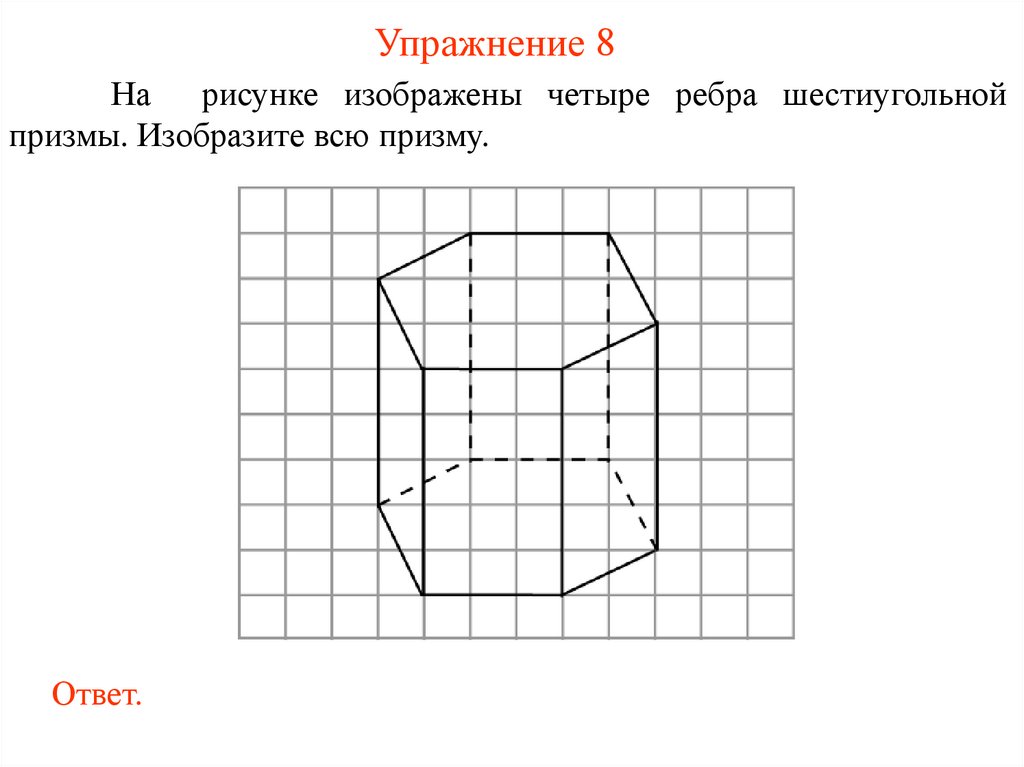
Упражнение 8На рисунке изображены четыре ребра шестиугольной
призмы. Изобразите всю призму.
Ответ.
14.
Упражнение 9На рисунке изображены четыре ребра шестиугольной
призмы. Изобразите всю призму.
Ответ.
15.
5б. Параллельность прямых впространстве
(Призма)
16.
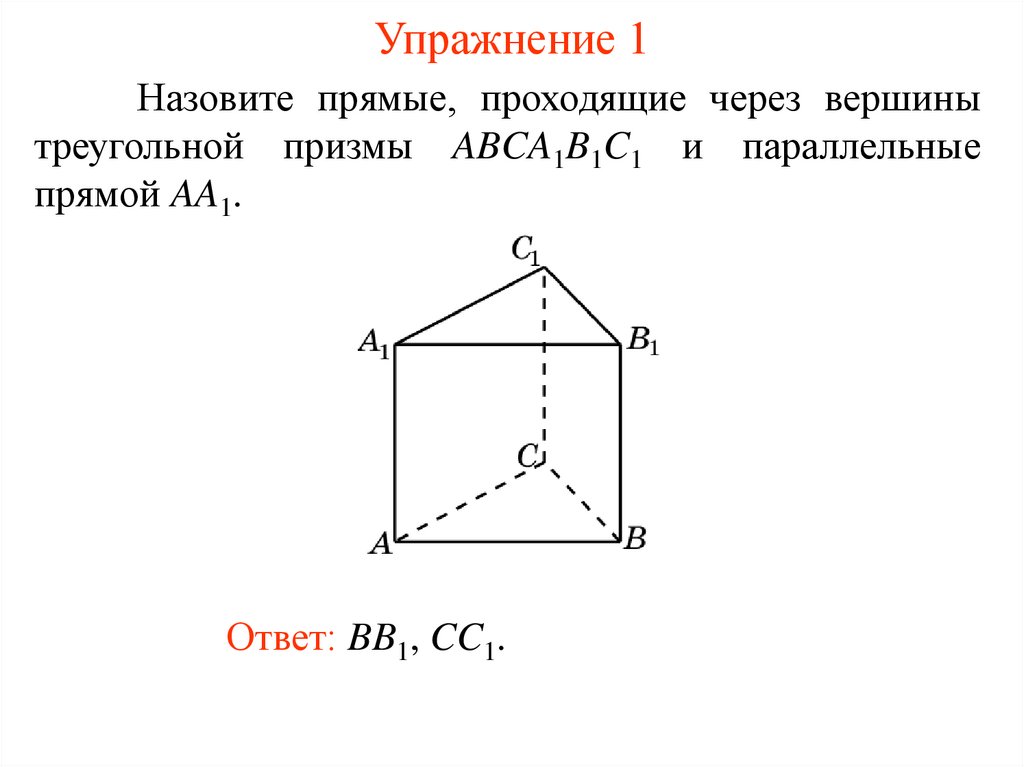
Упражнение 1Назовите прямые, проходящие через вершины
треугольной призмы ABCA1B1C1 и параллельные
прямой AA1.
Ответ: BB1, CC1.
17.
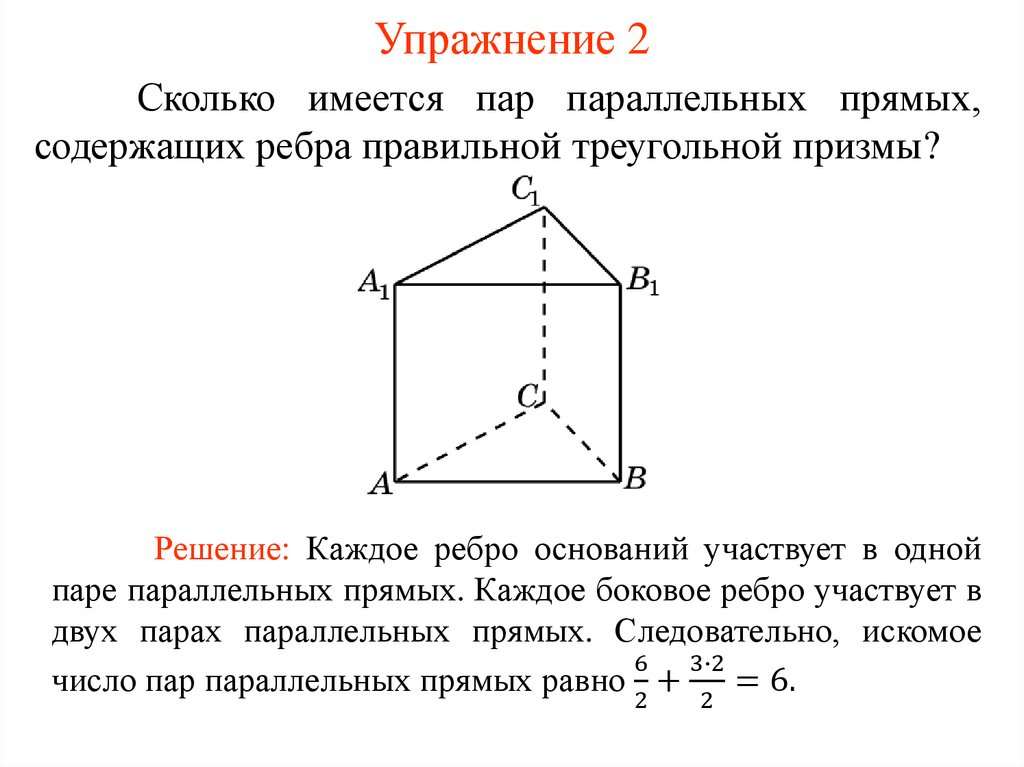
Упражнение 2Сколько имеется пар параллельных прямых,
содержащих ребра правильной треугольной призмы?
Решение: Каждое ребро оснований участвует в одной
паре параллельных прямых. Каждое боковое ребро участвует в
двух парах параллельных прямых. Следовательно, искомое
6
3∙2
число пар параллельных прямых равно +
= 6.
2
2
18.
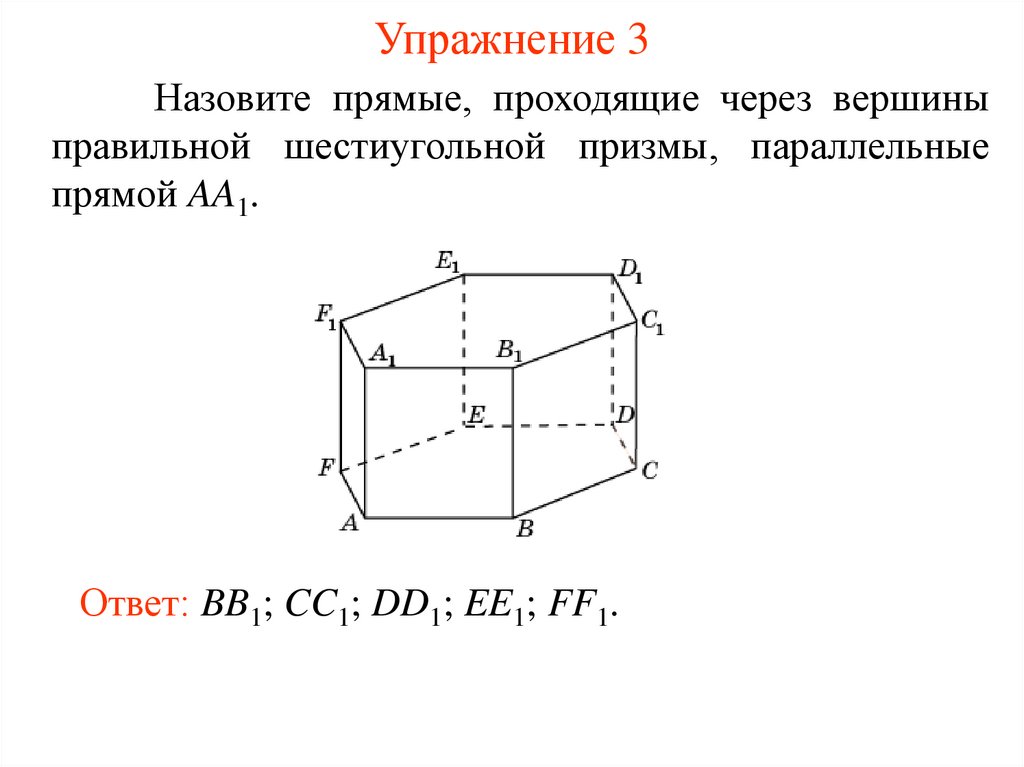
Упражнение 3Назовите прямые, проходящие через вершины
правильной шестиугольной призмы, параллельные
прямой AA1.
Ответ: BB1; CC1; DD1; EE1; FF1.
19.
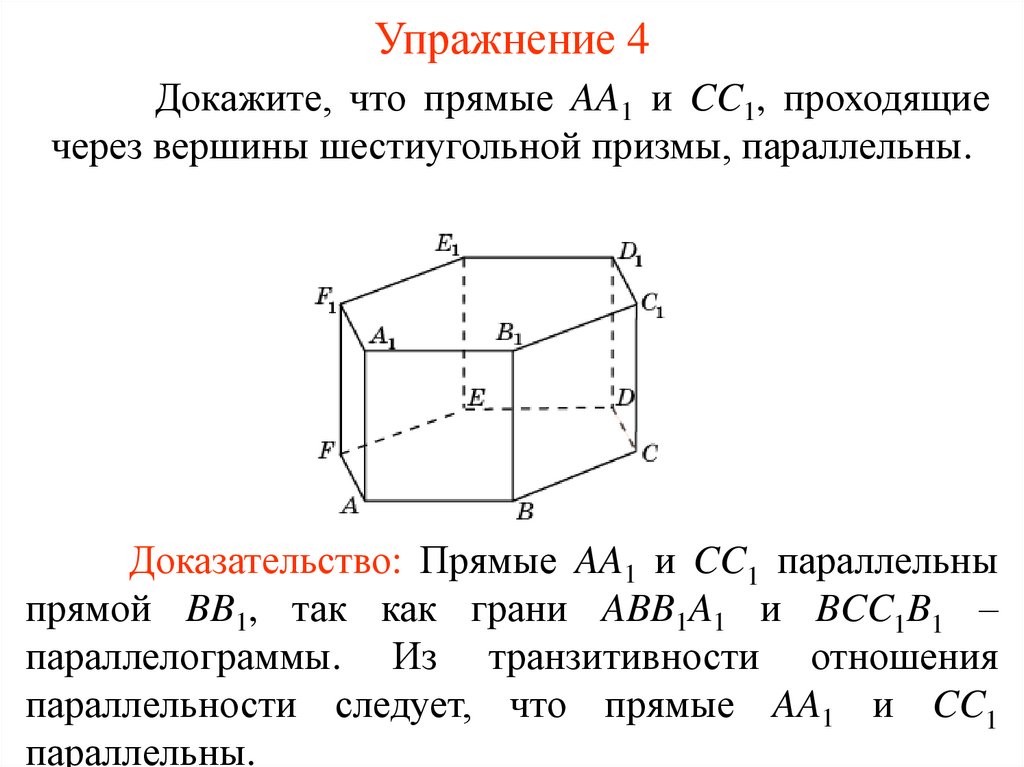
Упражнение 4Докажите, что прямые AA1 и CC1, проходящие
через вершины шестиугольной призмы, параллельны.
Доказательство: Прямые AA1 и CC1 параллельны
прямой BB1, так как грани ABB1A1 и BCC1B1 –
параллелограммы. Из транзитивности отношения
параллельности следует, что прямые AA1 и CC1
параллельны.
20.
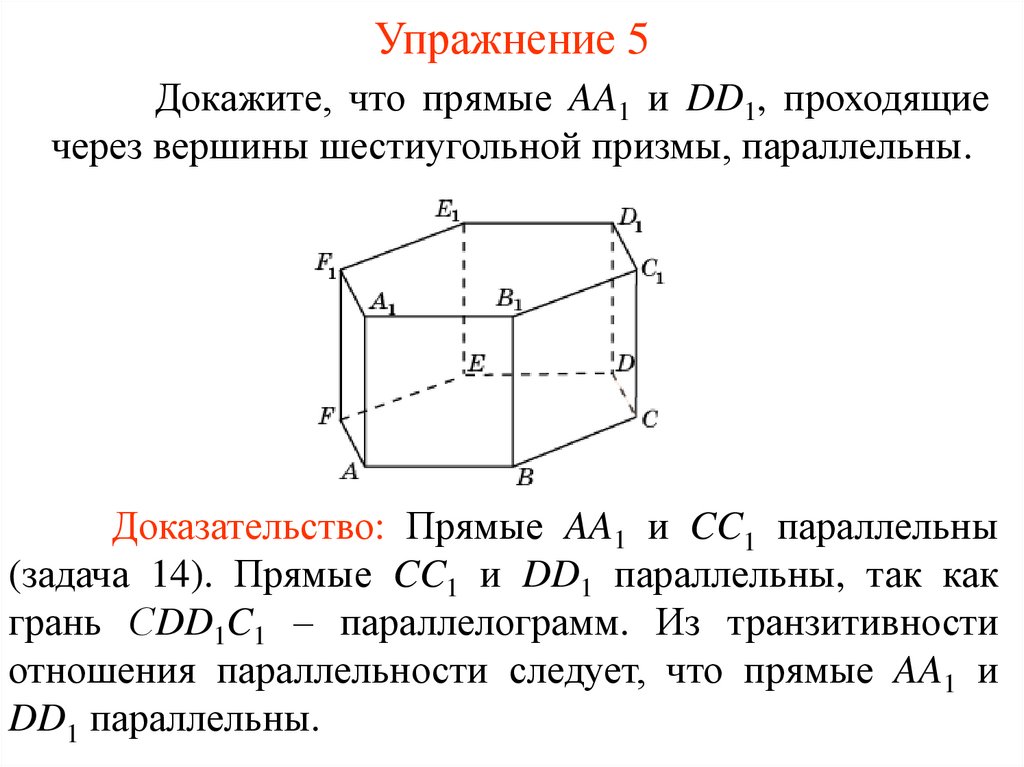
Упражнение 5Докажите, что прямые AA1 и DD1, проходящие
через вершины шестиугольной призмы, параллельны.
Доказательство: Прямые AA1 и CC1 параллельны
(задача 14). Прямые CC1 и DD1 параллельны, так как
грань СDD1C1 – параллелограмм. Из транзитивности
отношения параллельности следует, что прямые AA1 и
DD1 параллельны.
21.
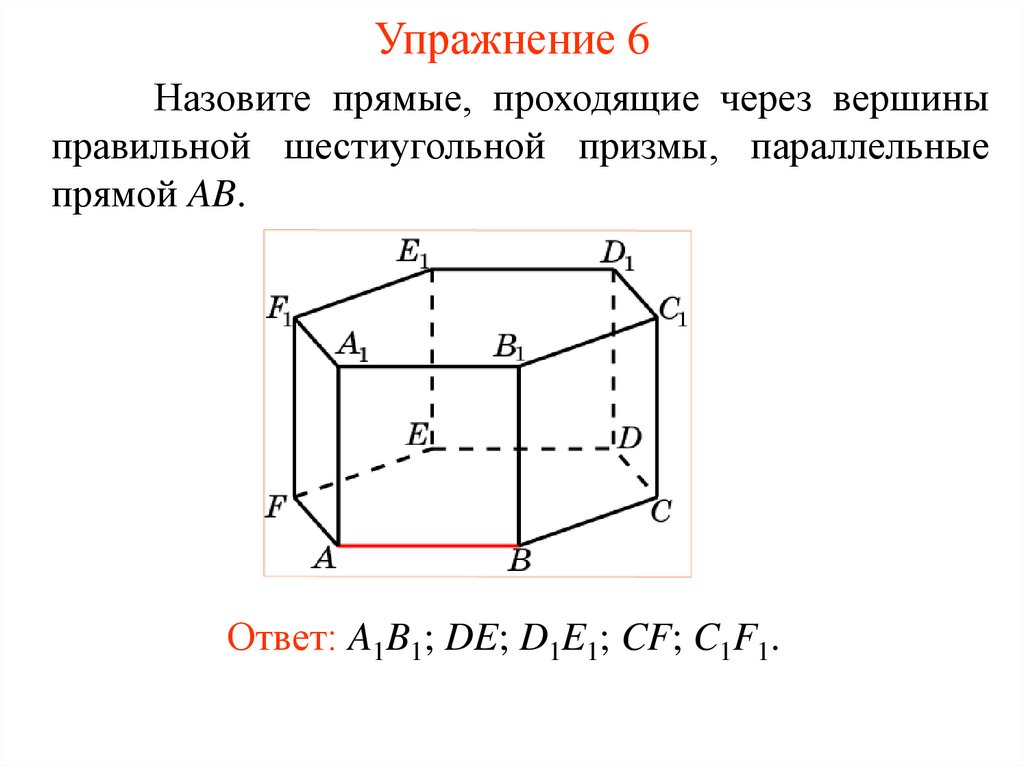
Упражнение 6Назовите прямые, проходящие через вершины
правильной шестиугольной призмы, параллельные
прямой AB.
Ответ: A1B1; DE; D1E1; CF; C1F1.
22.
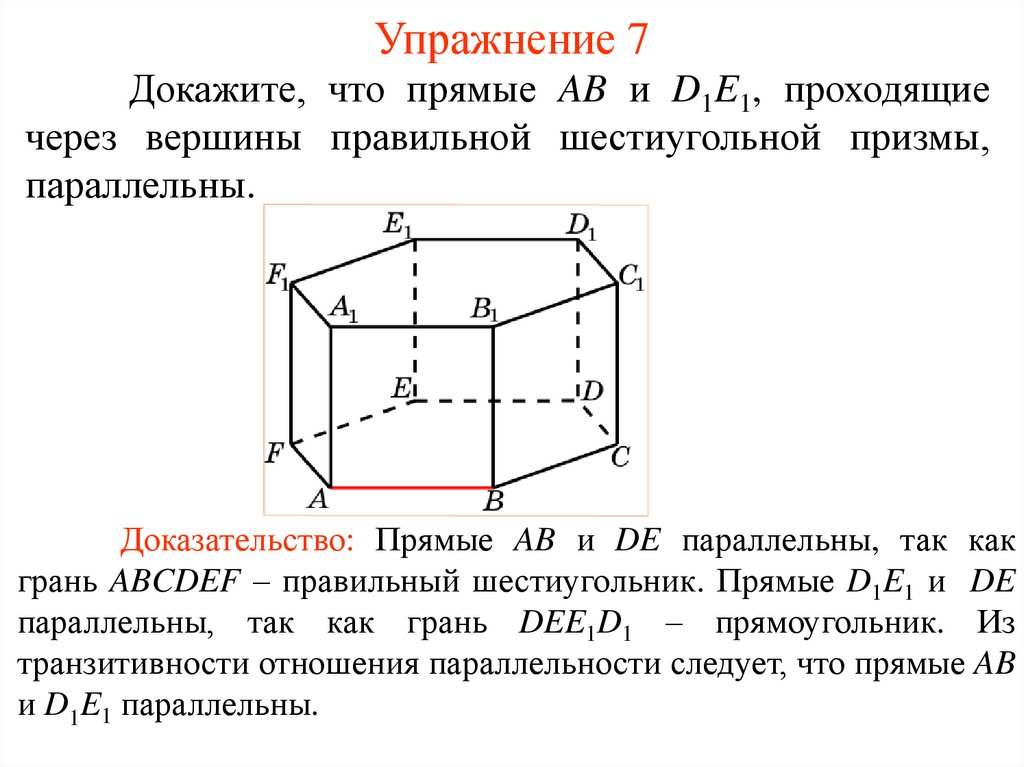
Упражнение 7Докажите, что прямые AB и D1E1, проходящие
через вершины правильной шестиугольной призмы,
параллельны.
Доказательство: Прямые AB и DE параллельны, так как
грань ABCDEF – правильный шестиугольник. Прямые D1E1 и DE
параллельны, так как грань DEE1D1 – прямоугольник. Из
транзитивности отношения параллельности следует, что прямые AB
и D1E1 параллельны.
23.
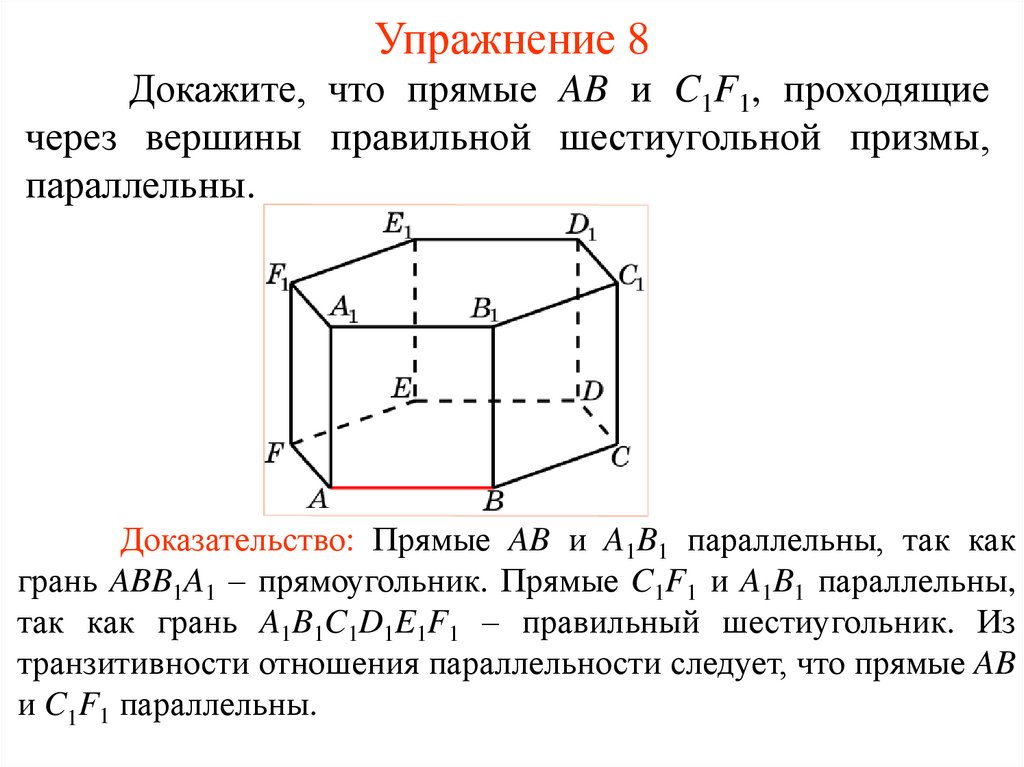
Упражнение 8Докажите, что прямые AB и C1F1, проходящие
через вершины правильной шестиугольной призмы,
параллельны.
Доказательство: Прямые AB и A1B1 параллельны, так как
грань ABB1A1 – прямоугольник. Прямые C1F1 и A1B1 параллельны,
так как грань A1B1C1D1E1F1 – правильный шестиугольник. Из
транзитивности отношения параллельности следует, что прямые AB
и C1F1 параллельны.
24.
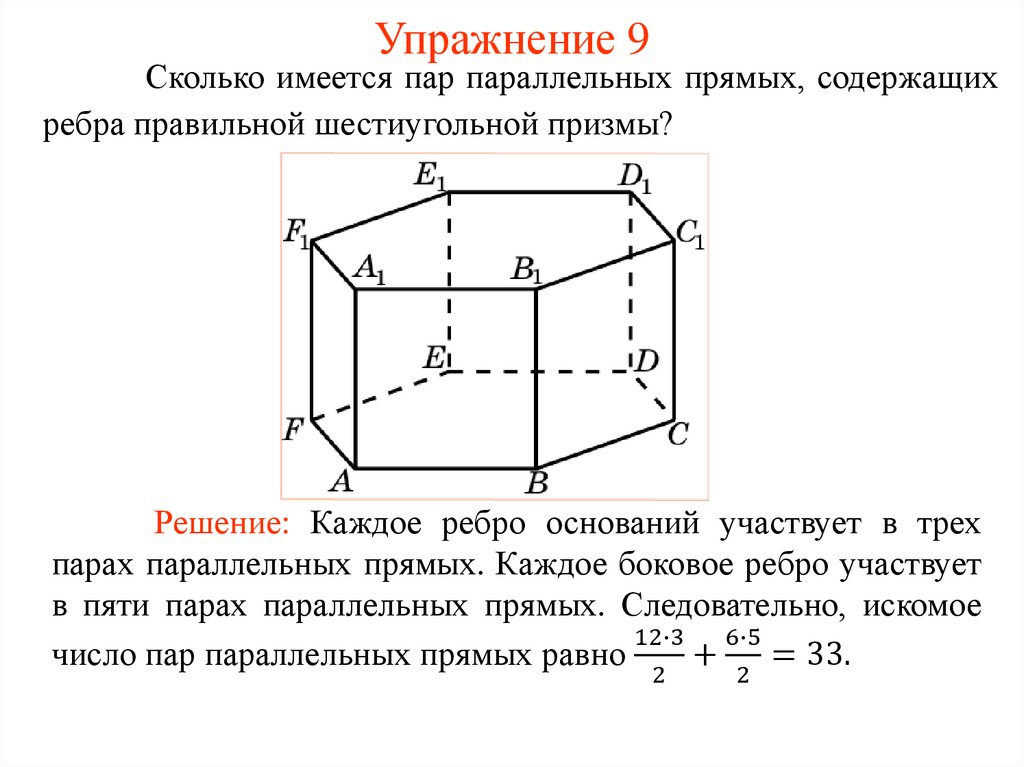
Упражнение 9Сколько имеется пар параллельных прямых, содержащих
ребра правильной шестиугольной призмы?
Решение: Каждое ребро оснований участвует в трех
парах параллельных прямых. Каждое боковое ребро участвует
в пяти парах параллельных прямых. Следовательно, искомое
12∙3
6∙5
число пар параллельных прямых равно
+
= 33.
2
2
25.
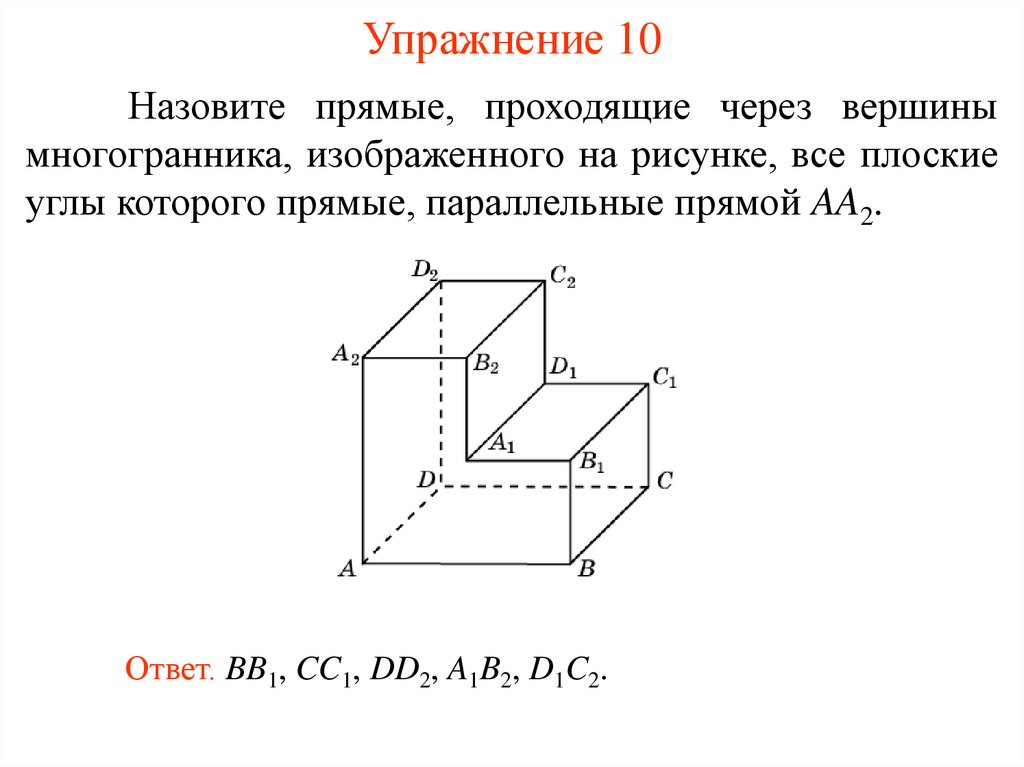
Упражнение 10Назовите прямые, проходящие через вершины
многогранника, изображенного на рисунке, все плоские
углы которого прямые, параллельные прямой AA2.
Ответ. BB1, CC1, DD2, A1B2, D1C2.
26.
6б. СКРЕЩИВАЮЩИЕСЯПРЯМЫЕ
(Призма, пирамида)
27.
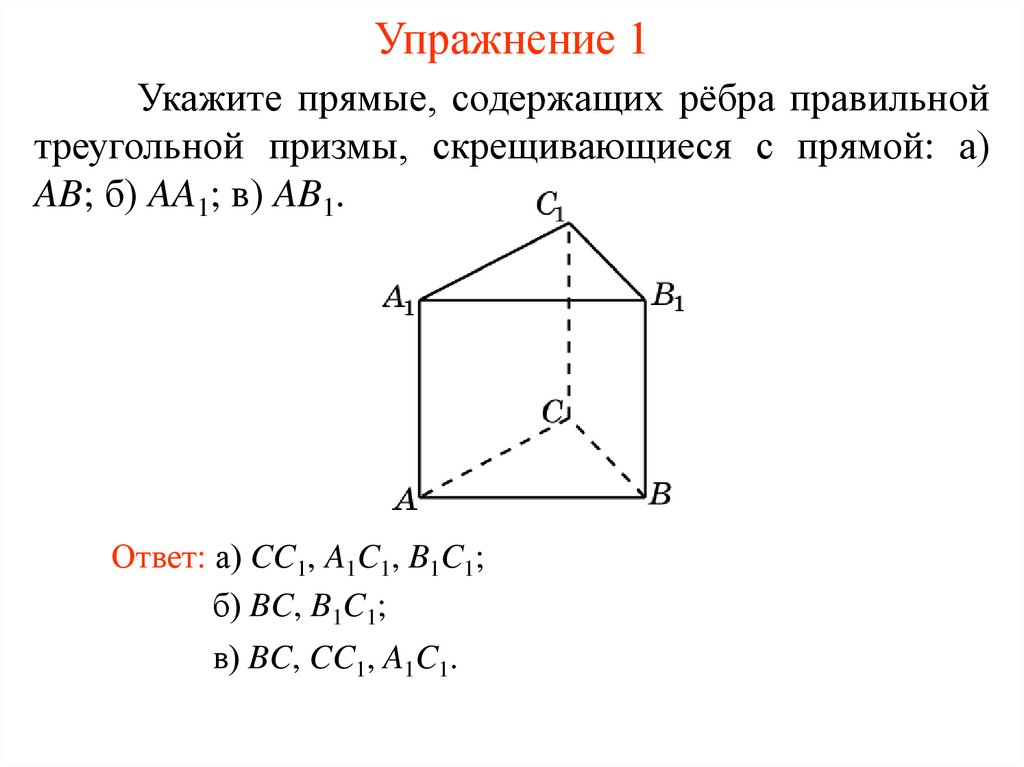
Упражнение 1Укажите прямые, содержащих рёбра правильной
треугольной призмы, скрещивающиеся с прямой: а)
AB; б) AA1; в) AB1.
Ответ: а) CC1, A1C1, B1C1;
б) BC, B1C1;
в) BC, CC1, A1C1.
28.
Домашняя работа к7.12
29.
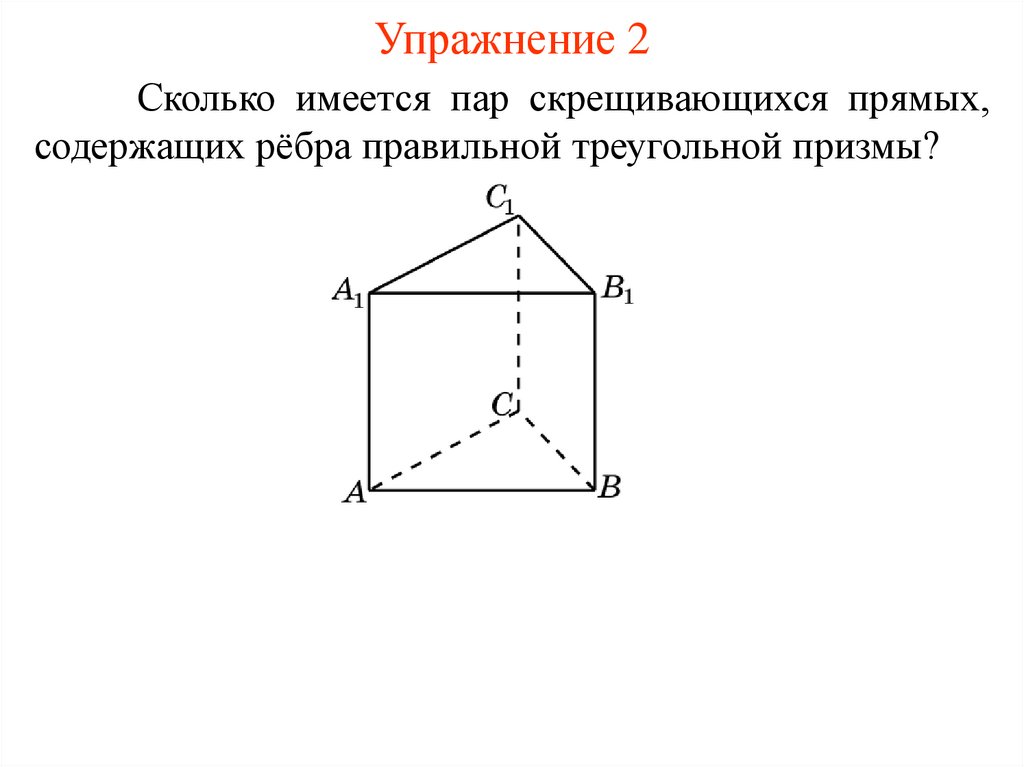
Упражнение 2Сколько имеется пар скрещивающихся прямых,
содержащих рёбра правильной треугольной призмы?
30.
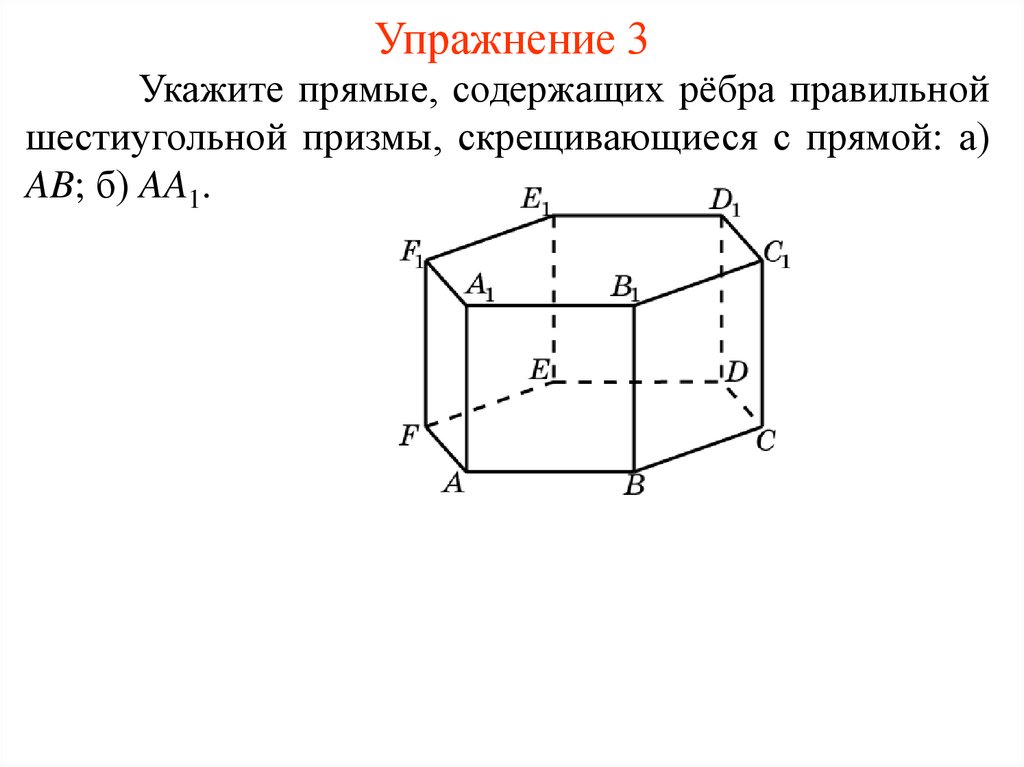
Упражнение 3Укажите прямые, содержащих рёбра правильной
шестиугольной призмы, скрещивающиеся с прямой: а)
AB; б) AA1.
31.
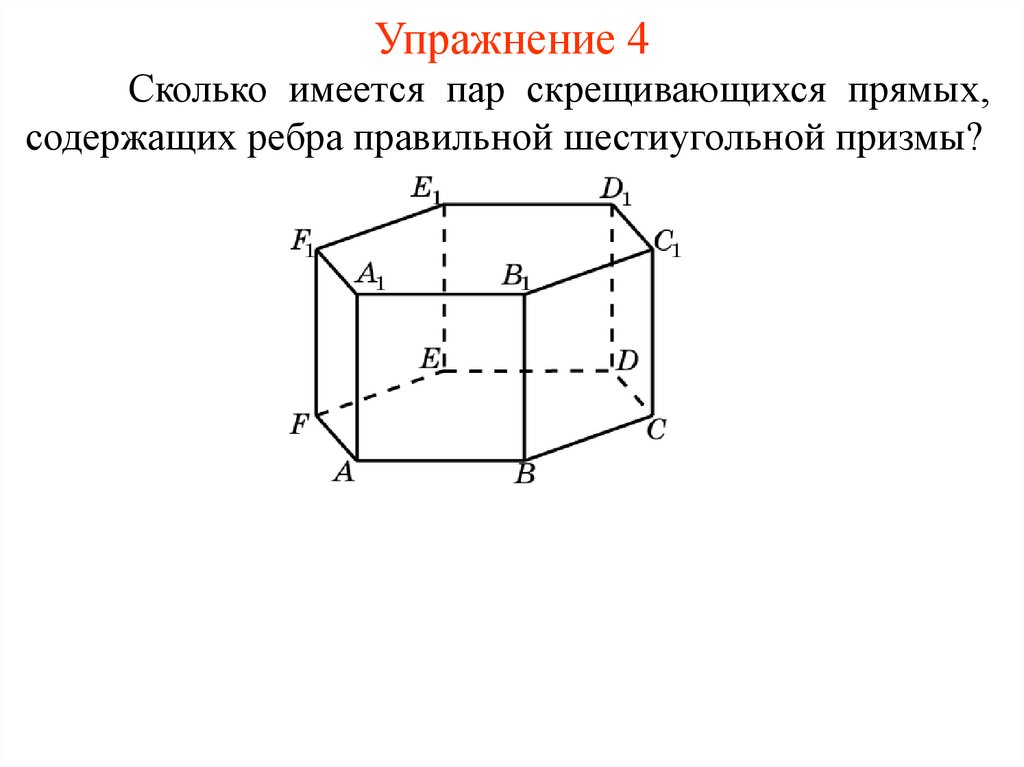
Упражнение 4Сколько имеется пар скрещивающихся прямых,
содержащих ребра правильной шестиугольной призмы?
32.
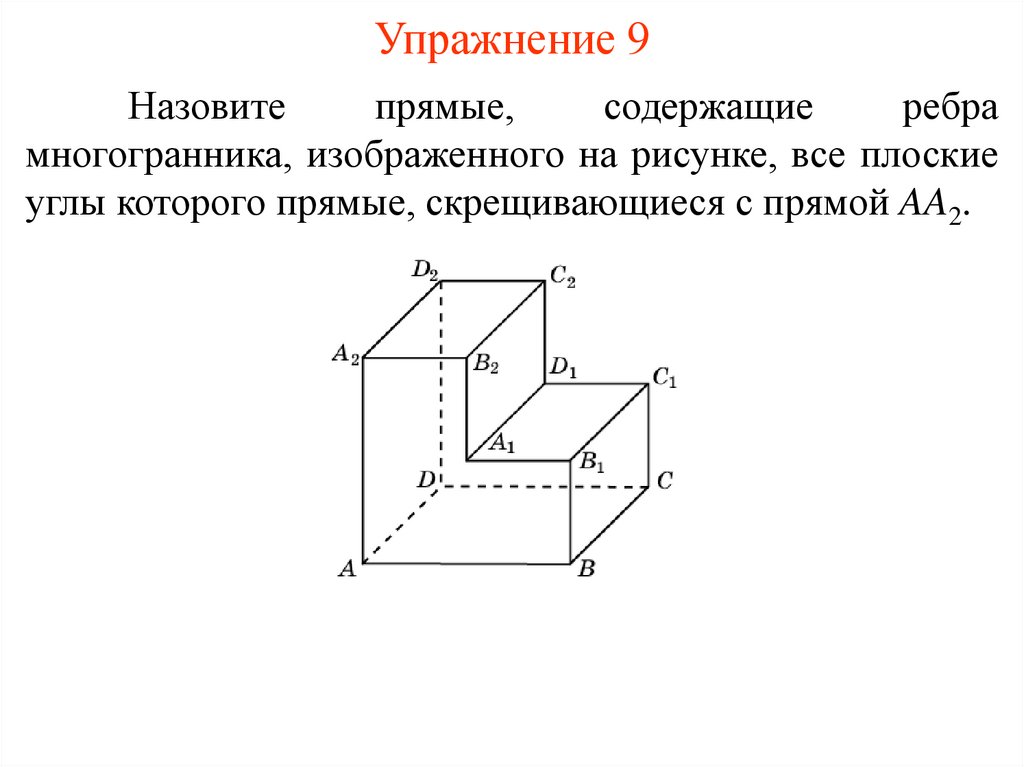
Упражнение 9Назовите
прямые,
содержащие
ребра
многогранника, изображенного на рисунке, все плоские
углы которого прямые, скрещивающиеся с прямой AA2.
33.
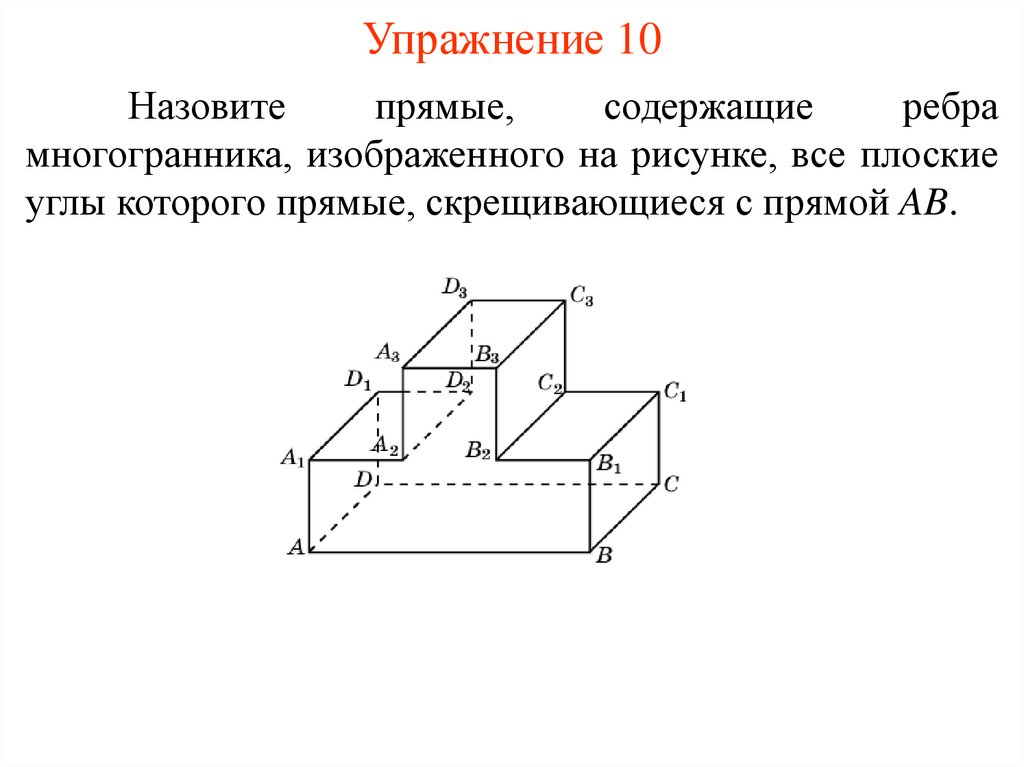
Упражнение 10Назовите
прямые,
содержащие
ребра
многогранника, изображенного на рисунке, все плоские
углы которого прямые, скрещивающиеся с прямой AB.
34.
7б. ПАРАЛЛЕЛЬНОСТЬПРЯМОЙ И ПЛОСКОСТИ
(Пирамида, призма)
35.
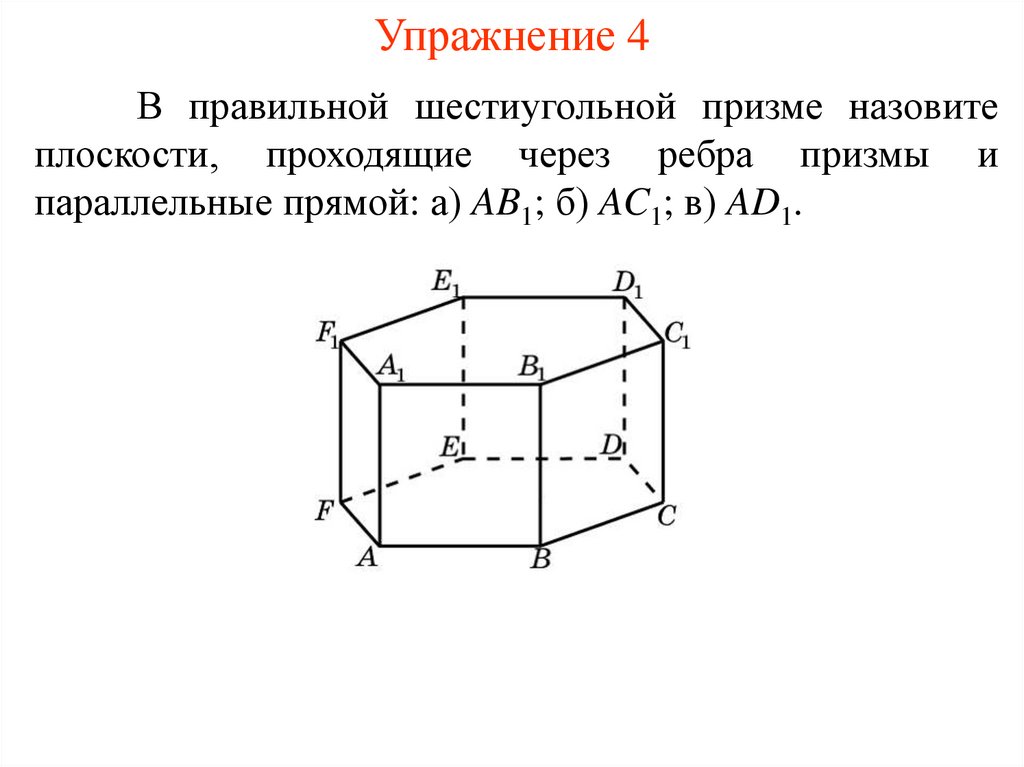
Упражнение 4В правильной шестиугольной призме назовите
плоскости, проходящие через ребра призмы и
параллельные прямой: а) AB1; б) AC1; в) AD1.
36.
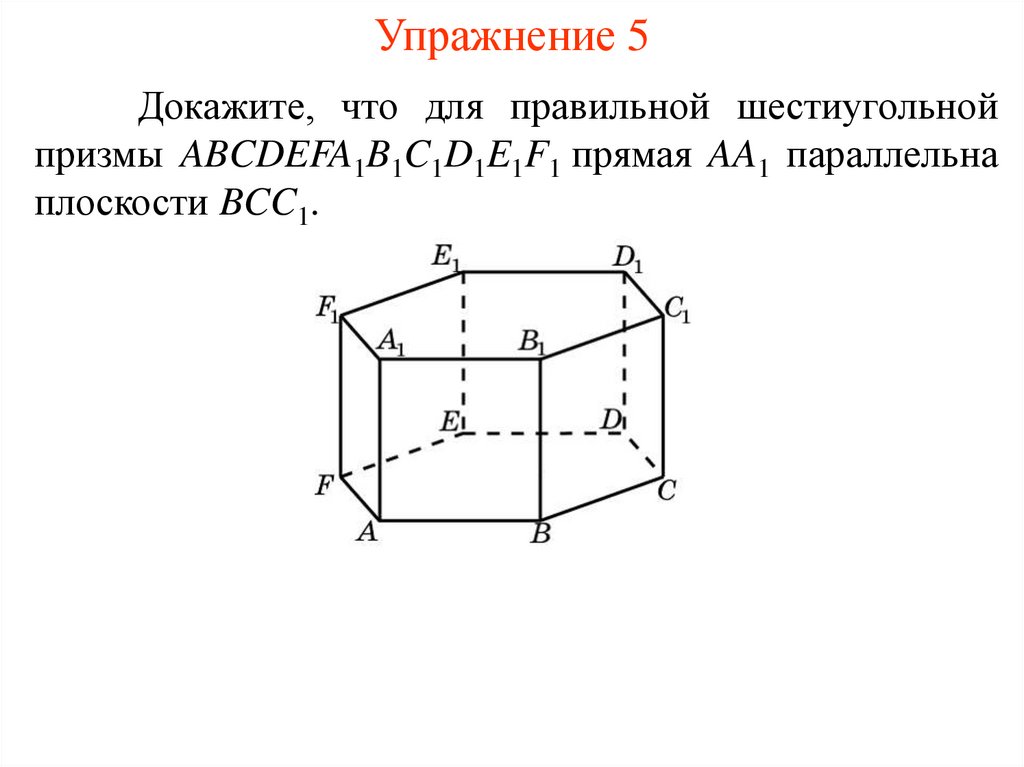
Упражнение 5Докажите, что для правильной шестиугольной
призмы ABCDEFA1B1C1D1E1F1 прямая AA1 параллельна
плоскости BCC1.
37.
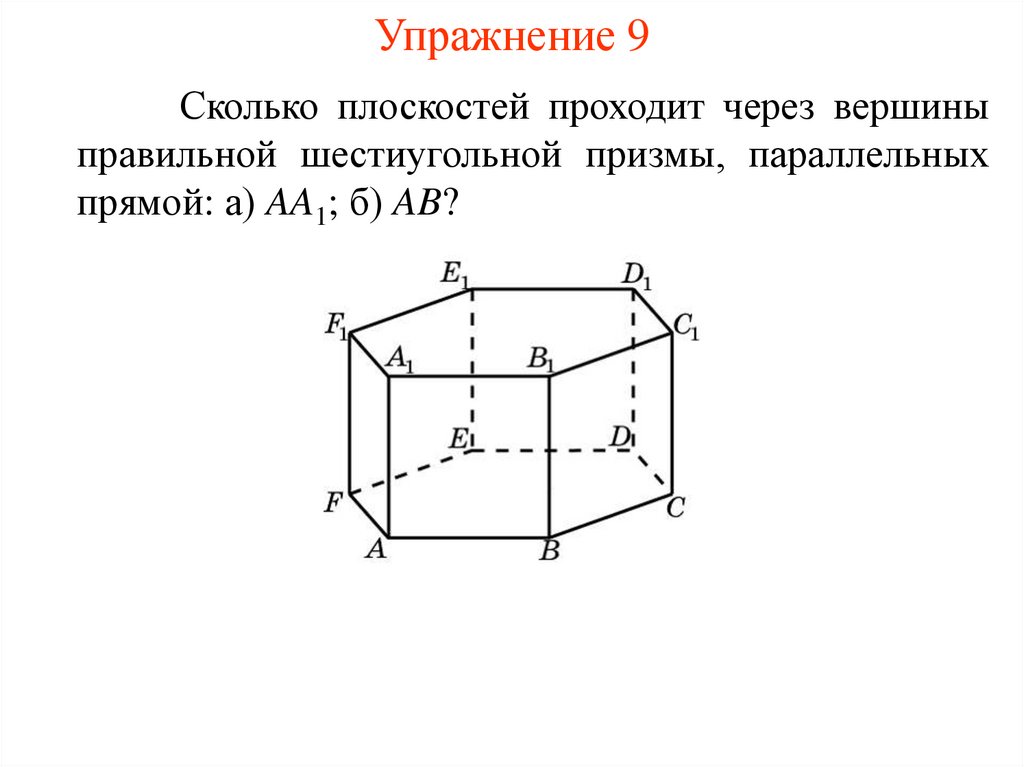
Упражнение 9Сколько плоскостей проходит через вершины
правильной шестиугольной призмы, параллельных
прямой: а) AA1; б) AB?
38.
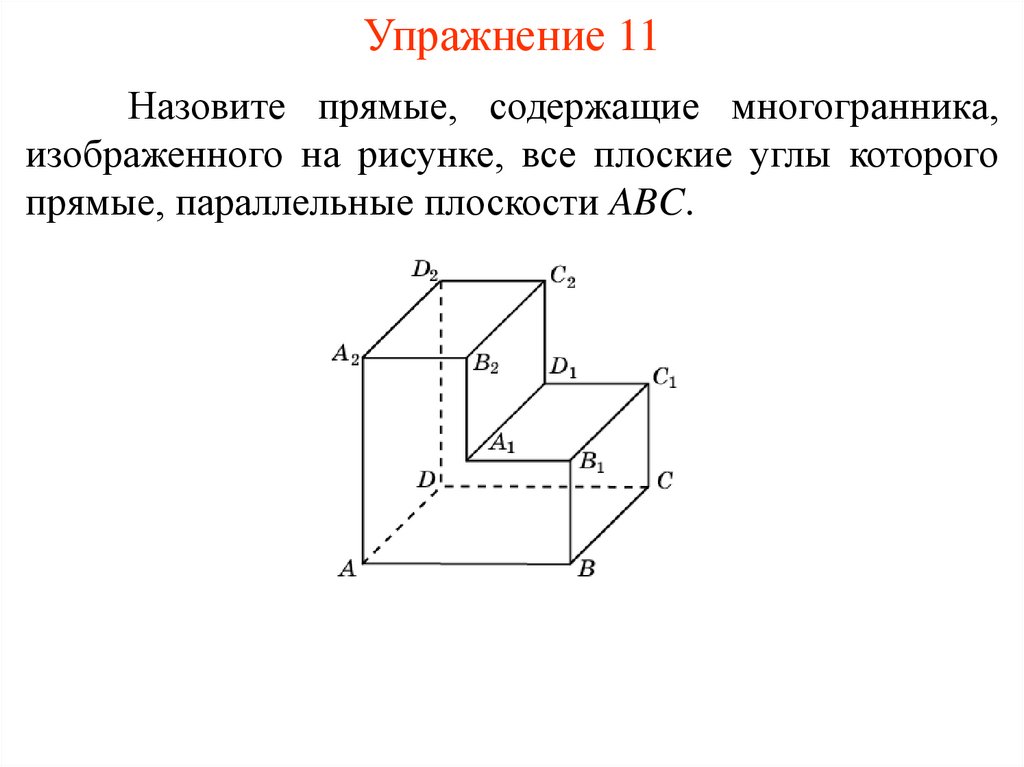
Упражнение 11Назовите прямые, содержащие многогранника,
изображенного на рисунке, все плоские углы которого
прямые, параллельные плоскости ABC.
39.
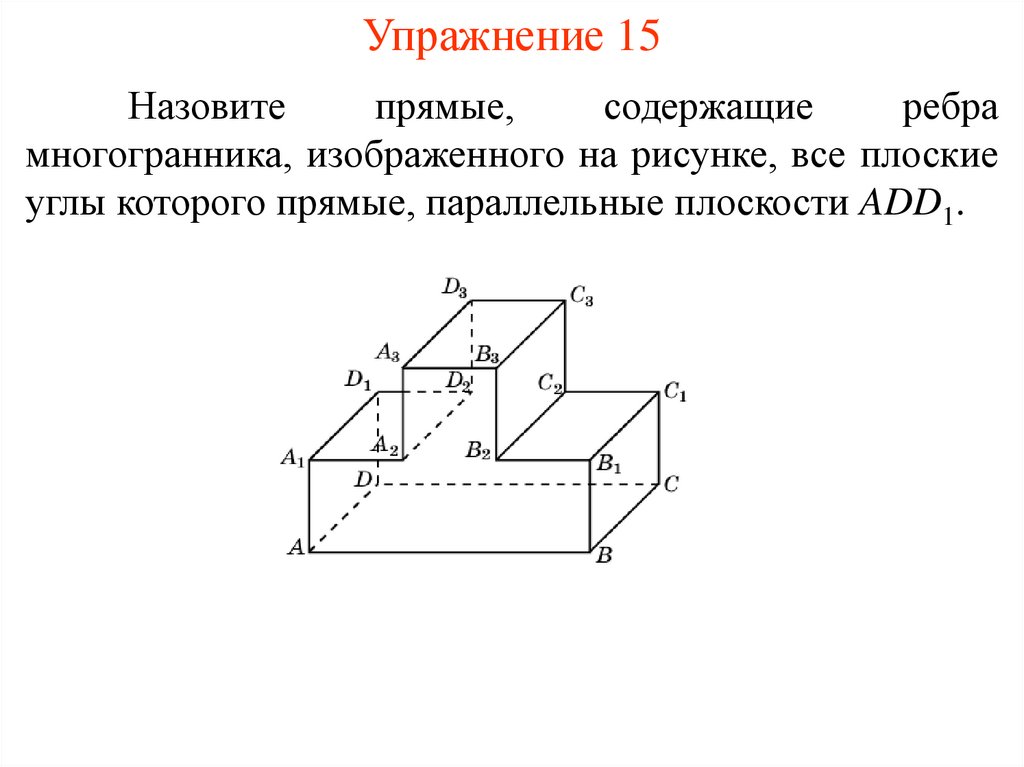
Упражнение 15Назовите
прямые,
содержащие
ребра
многогранника, изображенного на рисунке, все плоские
углы которого прямые, параллельные плоскости ADD1.
40.
8б. ПАРАЛЛЕЛЬНОСТЬПЛОСКОСТЕЙ
(Призма)
41.
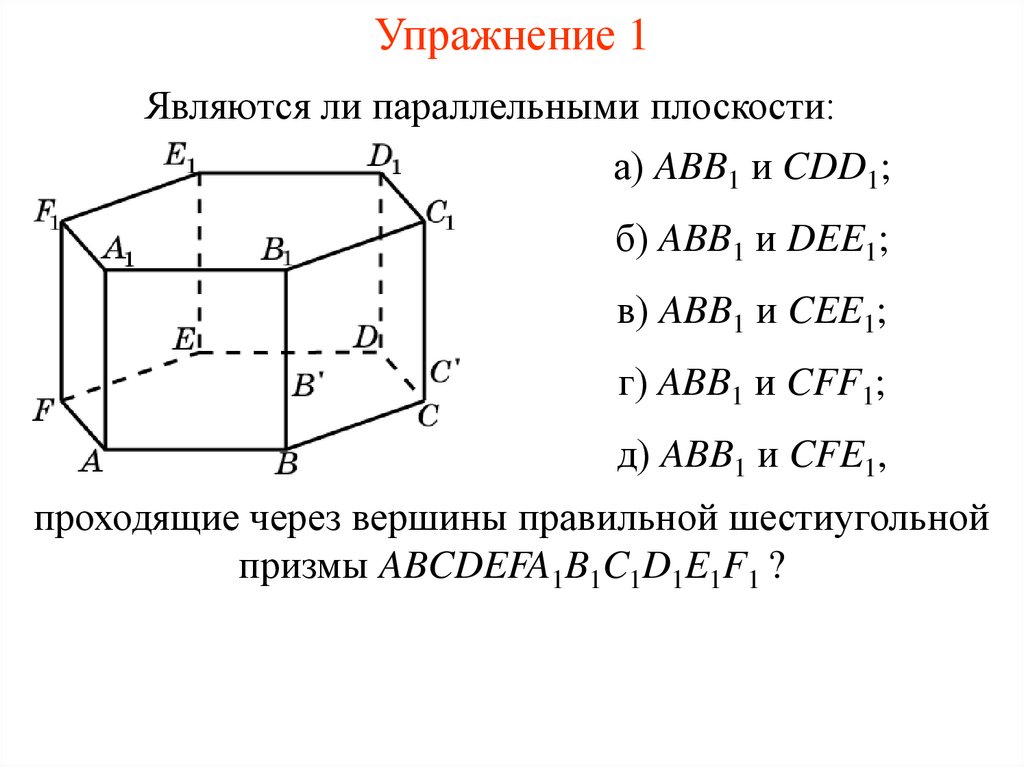
Упражнение 1Являются ли параллельными плоскости:
а) ABB1 и CDD1;
б) ABB1 и DEE1;
в) ABB1 и CEE1;
г) ABB1 и CFF1;
д) ABB1 и CFE1,
проходящие через вершины правильной шестиугольной
призмы ABCDEFA1B1C1D1E1F1 ?
42.
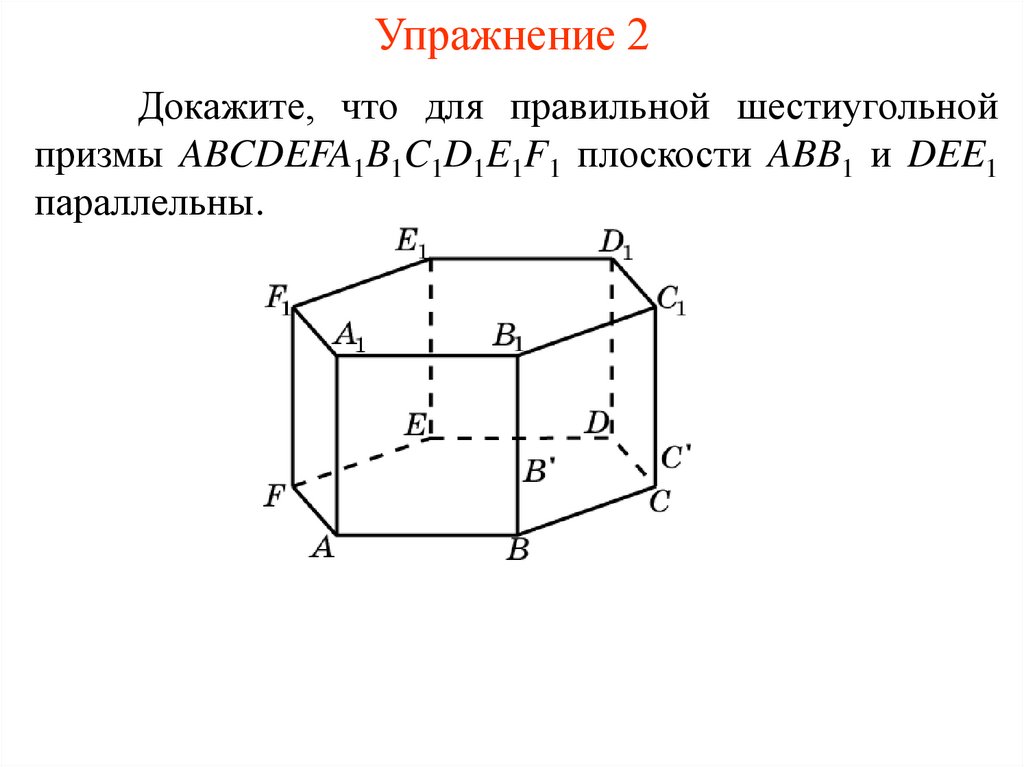
Упражнение 2Докажите, что для правильной шестиугольной
призмы ABCDEFA1B1C1D1E1F1 плоскости ABB1 и DEE1
параллельны.
43.
16б. УГОЛ МЕЖДУ ПРЯМЫМИ ВПРОСТРАНСТВЕ
(Призма)
44.
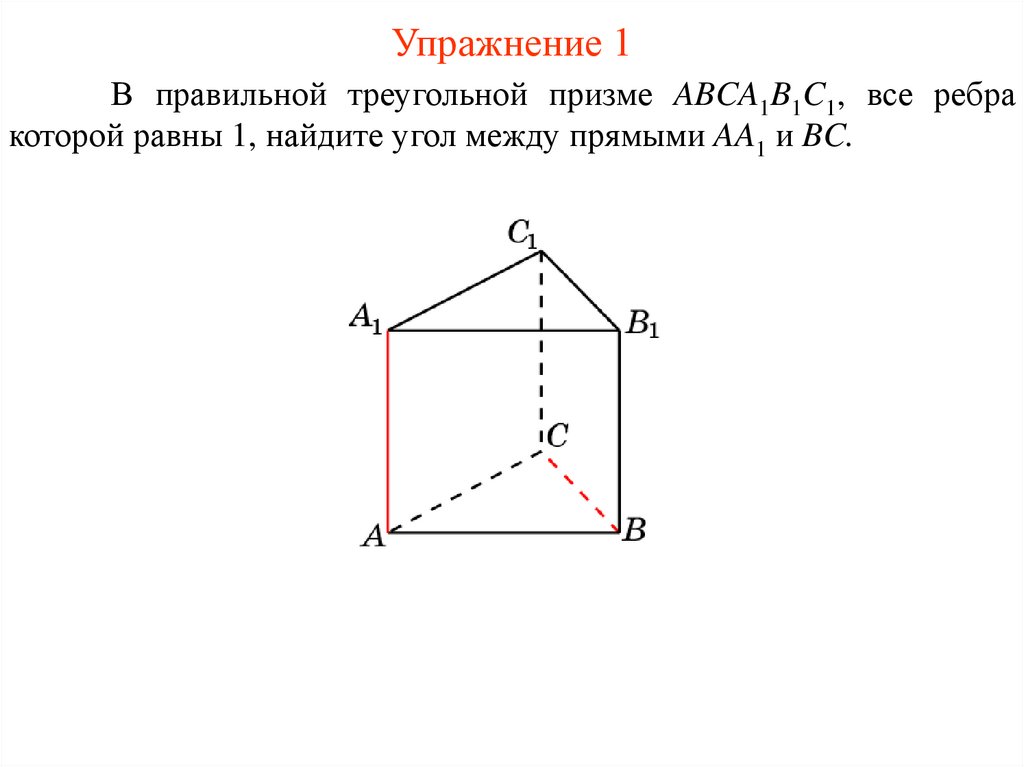
Упражнение 1В правильной треугольной призме ABCA1B1C1, все ребра
которой равны 1, найдите угол между прямыми AA1 и BC.
45.
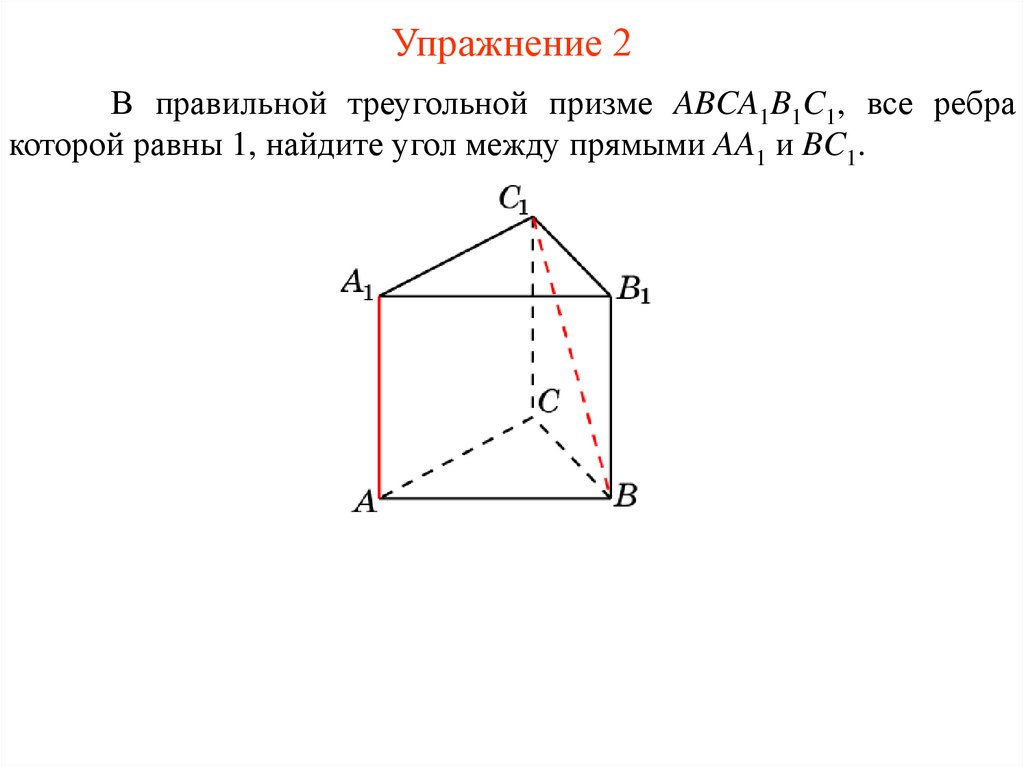
Упражнение 2В правильной треугольной призме ABCA1B1C1, все ребра
которой равны 1, найдите угол между прямыми AA1 и BC1.
46.
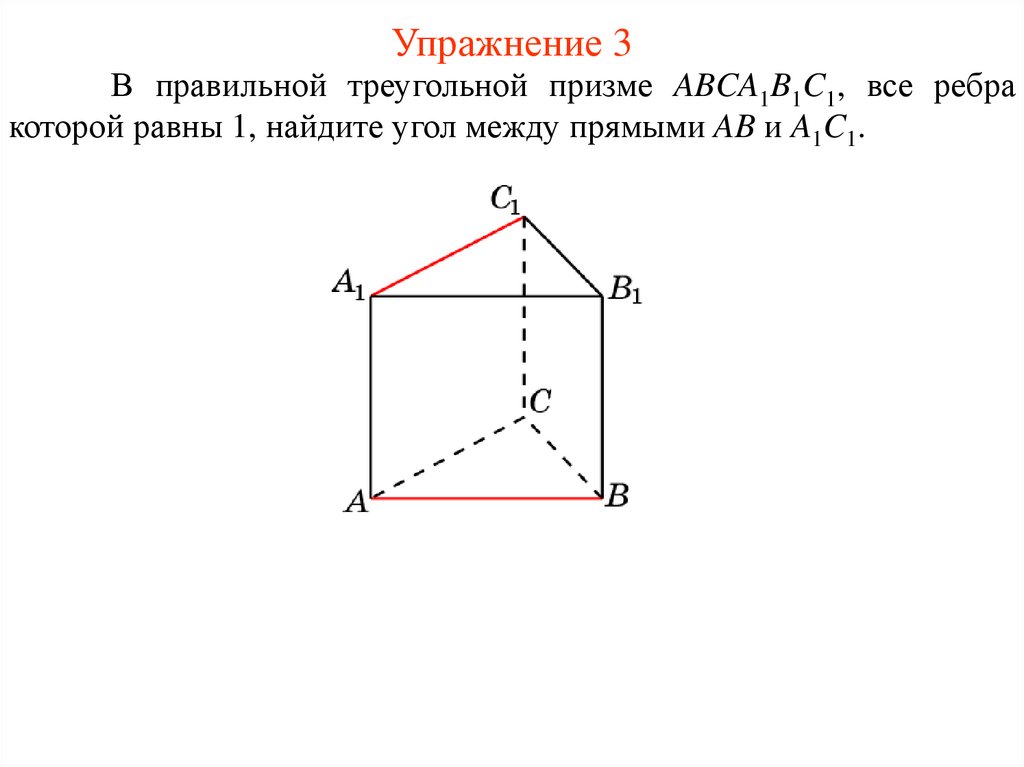
Упражнение 3В правильной треугольной призме ABCA1B1C1, все ребра
которой равны 1, найдите угол между прямыми AB и A1C1.
47.
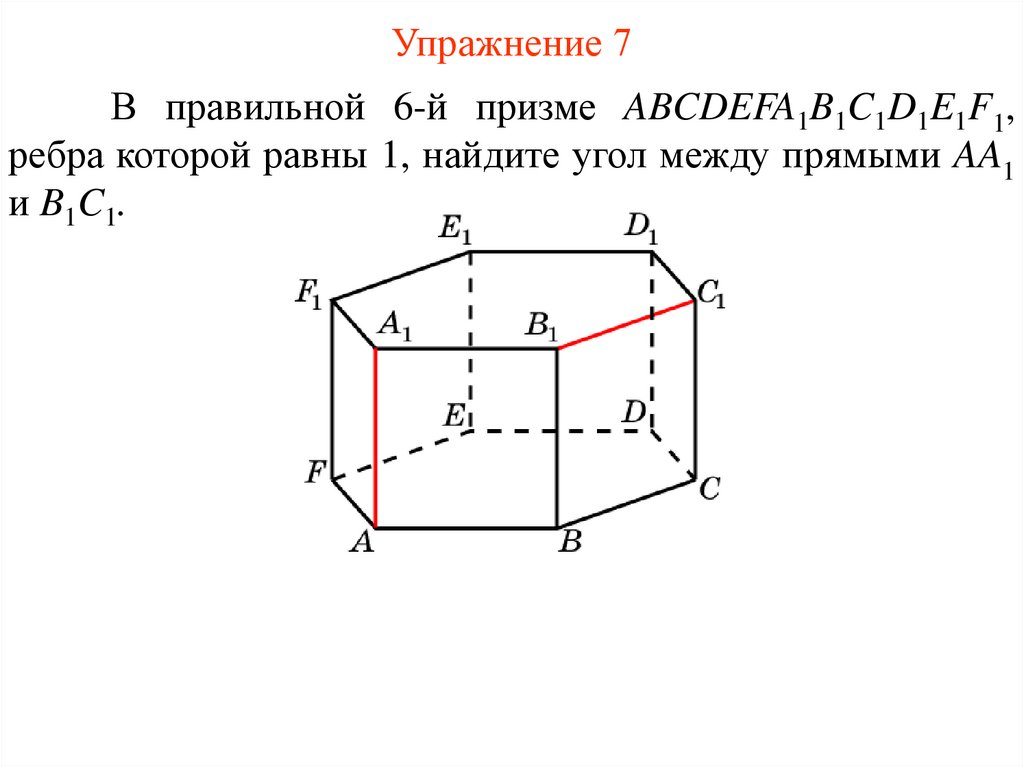
Упражнение 7В правильной 6-й призме ABCDEFA1B1C1D1E1F1,
ребра которой равны 1, найдите угол между прямыми AA1
и B1C1.
48.
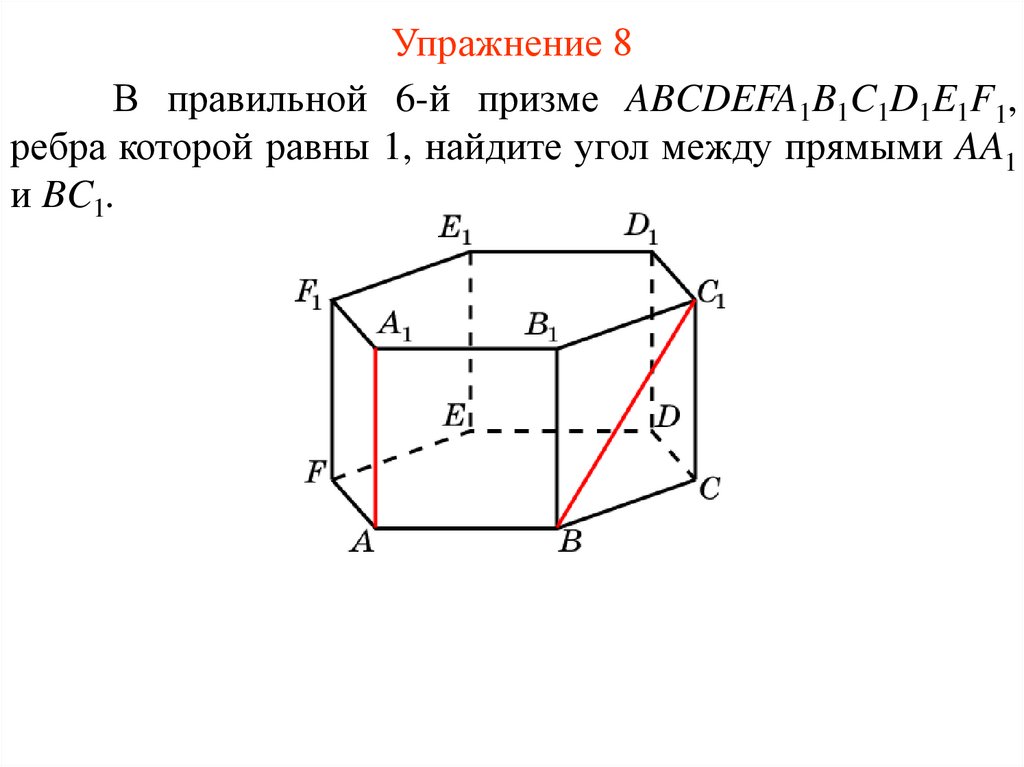
Упражнение 8В правильной 6-й призме ABCDEFA1B1C1D1E1F1,
ребра которой равны 1, найдите угол между прямыми AA1
и BC1.
49.
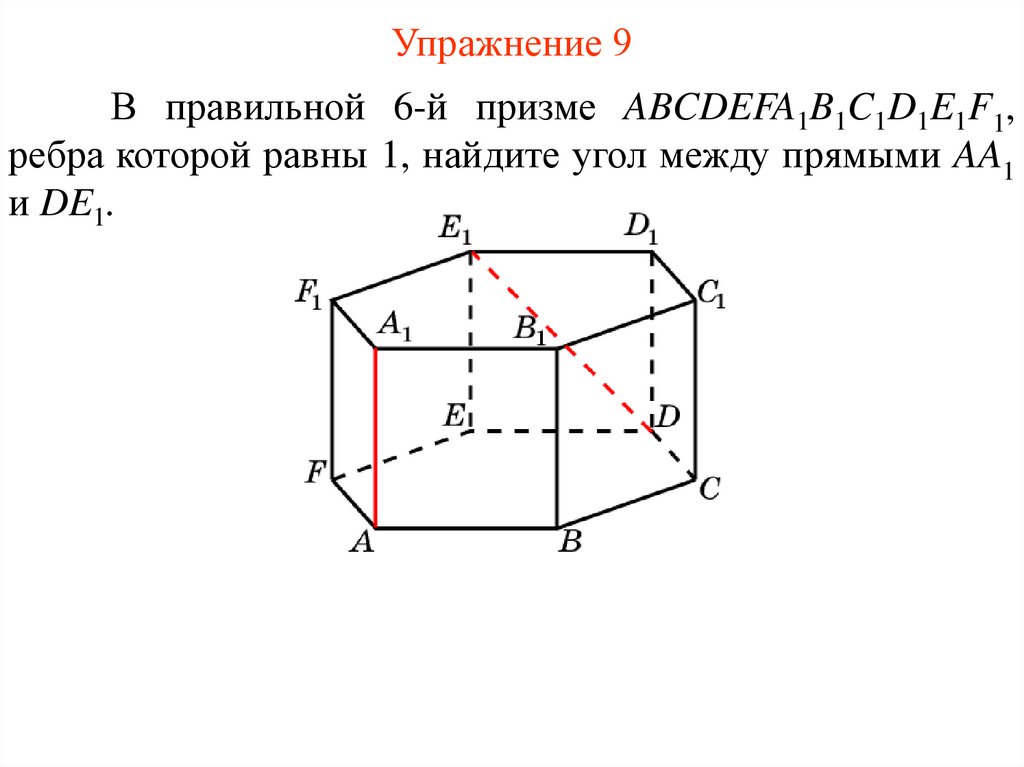
Упражнение 9В правильной 6-й призме ABCDEFA1B1C1D1E1F1,
ребра которой равны 1, найдите угол между прямыми AA1
и DE1.
50.
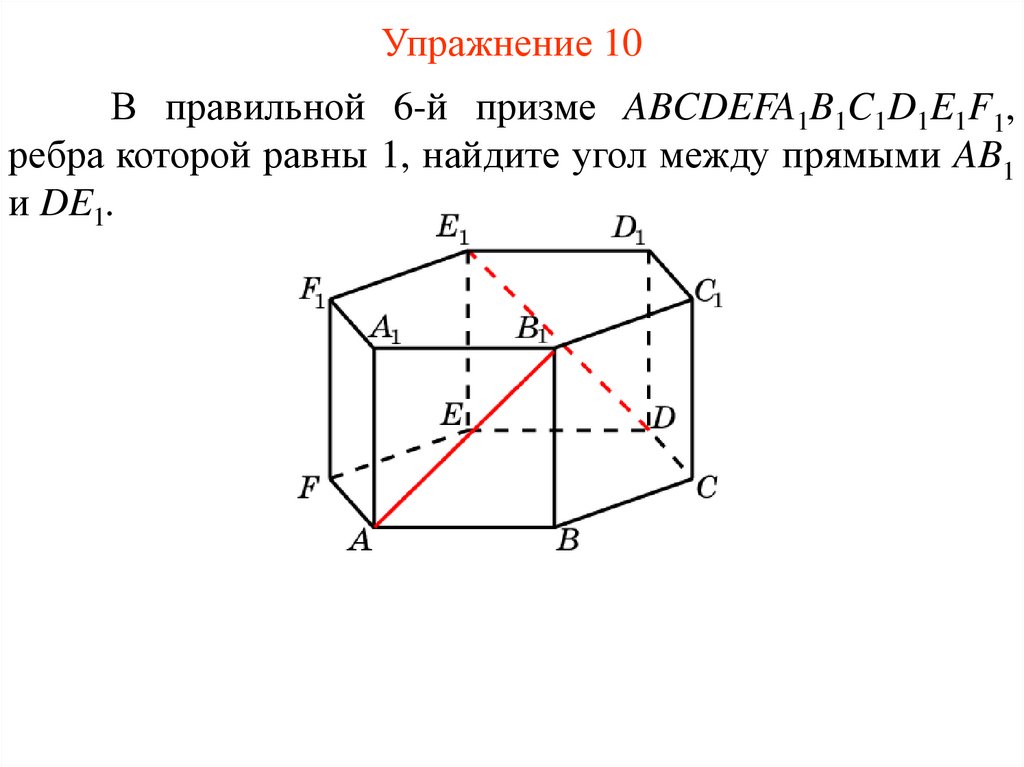
Упражнение 10В правильной 6-й призме ABCDEFA1B1C1D1E1F1,
ребра которой равны 1, найдите угол между прямыми AB1
и DE1.
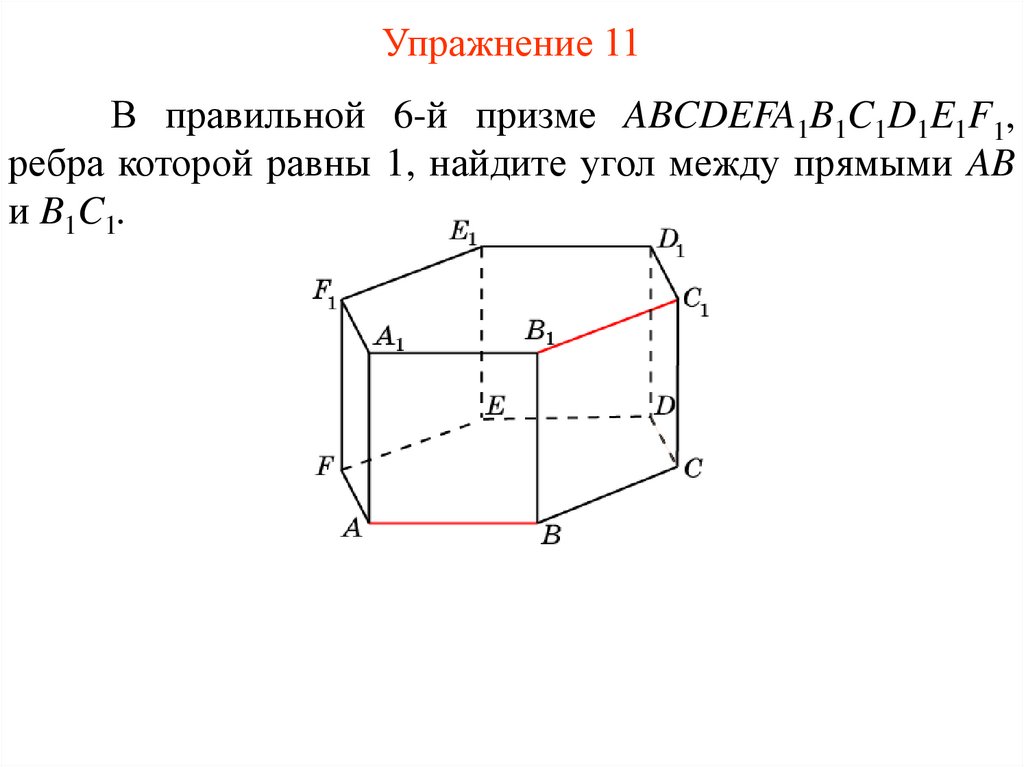
51.
Упражнение 11В правильной 6-й призме ABCDEFA1B1C1D1E1F1,
ребра которой равны 1, найдите угол между прямыми AB
и B1C1.
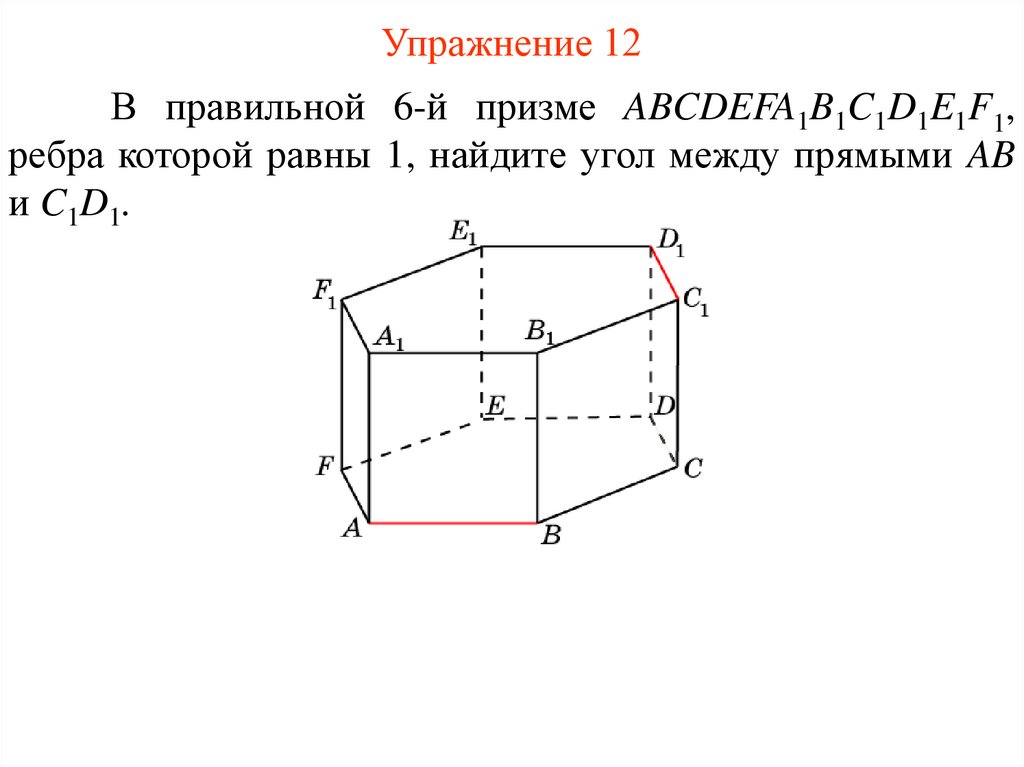
52.
Упражнение 12В правильной 6-й призме ABCDEFA1B1C1D1E1F1,
ребра которой равны 1, найдите угол между прямыми AB
и C1D1.














 mathematics
mathematics








