Понятие многогранника

1.

Понятие многогранника

2.

Содержание.
1. Вступление
2. Понятие многогранника
3. Характеристика Эйлера
4. Призма
5. Решение задач
6. Домашнее задание

3.

Как называются представленные фигуры?
Обратите внимание, что каждая из этих
поверхностей ограничивает некоторое
геометрическое тело, отделяет это тело от
остальной части пространства.

4.

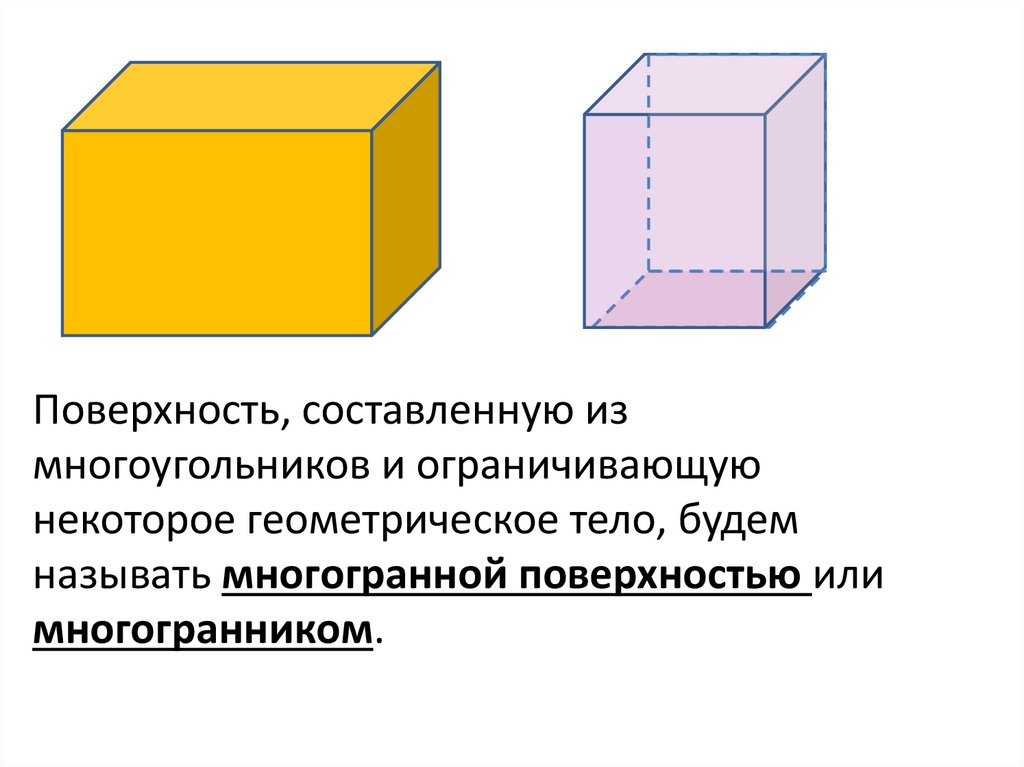
Поверхность, составленную из
многоугольников и ограничивающую
некоторое геометрическое тело, будем
называть многогранной поверхностью или
многогранником.

5.

Многие строения
в окружающем
нас мире имеют
форму
многогранников
или состоят из
нескольких
разных
многогранников

6.

Пирамида Хеопса
Памятник относится
к эпохе Древнего
царства (IV
династия).
Построена
племянником
фараона Хеопса
Хемиуном.
Поэтому для лучшей сохранности,
эксплуатации и моделирования здания
нужно изучить свойства многогранников.

7.

Многие многогранники изобрёл не
человек, а создала природа в виде
кристаллов:
Поваренная и каменная соль
Горный
хрусталь
Кристаллы
льда

8.

Кристаллы кварца
Кристаллы граната

9.

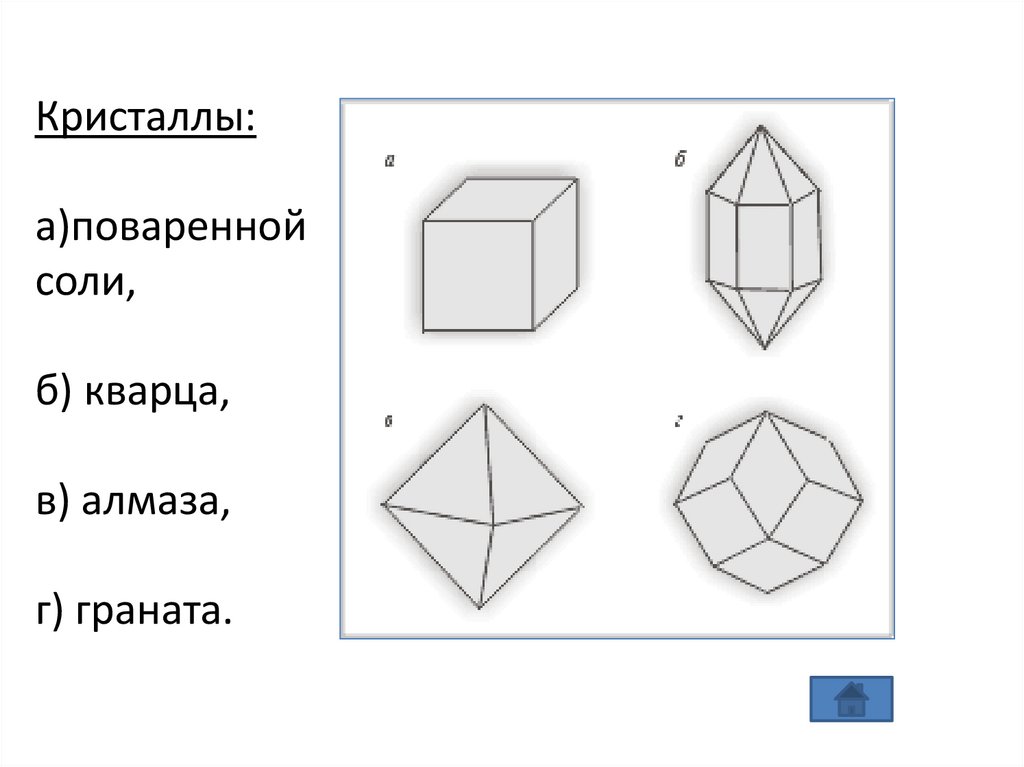
Кристаллы:
а)поваренной
соли,
б) кварца,
в) алмаза,
г) граната.

10.

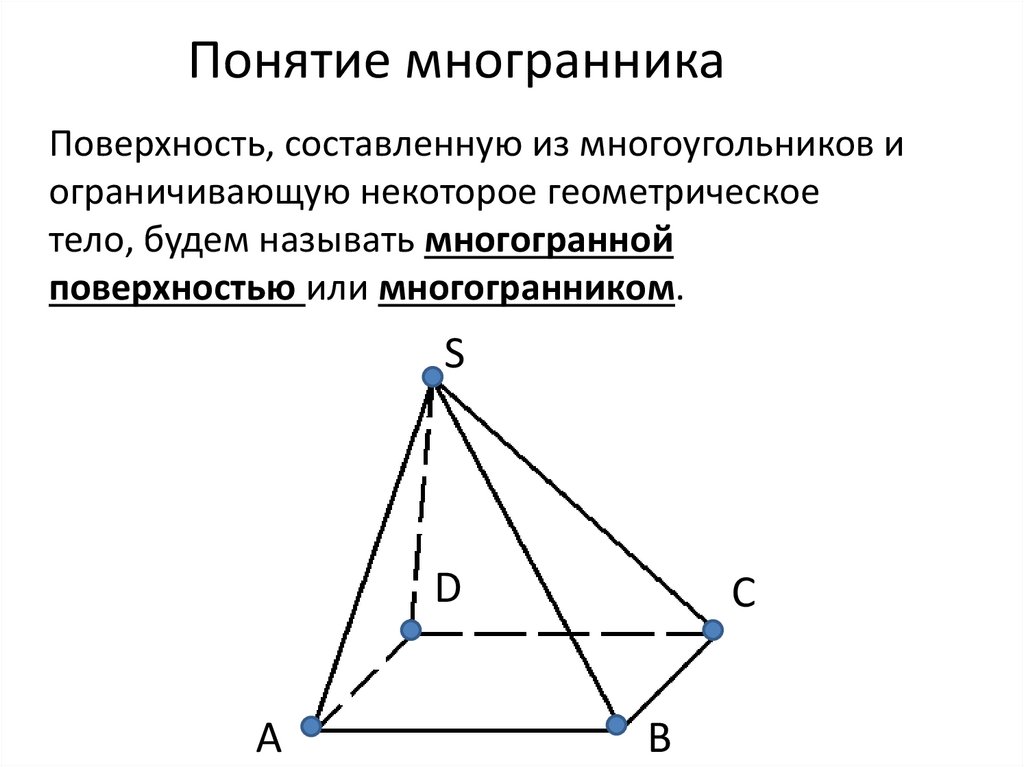
Понятие многранника
Поверхность, составленную из многоугольников и
ограничивающую некоторое геометрическое
тело, будем называть многогранной
поверхностью или многогранником.
S
D
A
C
B

11.

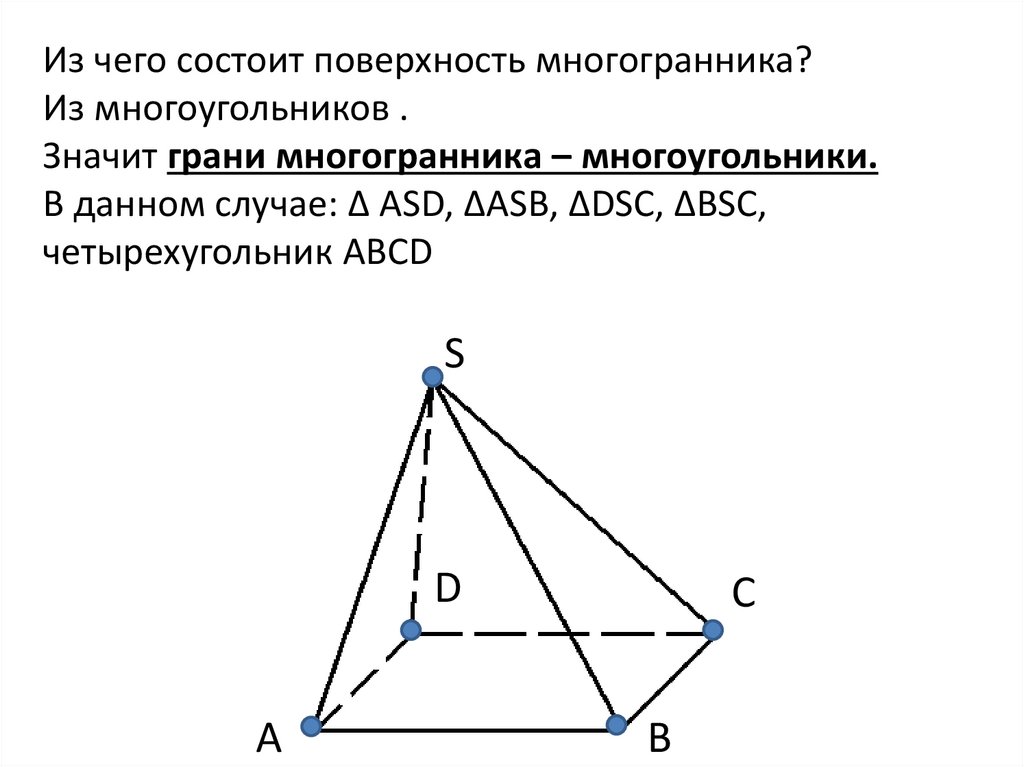
Из чего состоит поверхность многогранника?
Из многоугольников .
Значит грани многогранника – многоугольники.
В данном случае: Δ ASD, ΔASB, ΔDSC, ΔBSC,
четырехугольник ABCD
S
D
A
C
B

12.

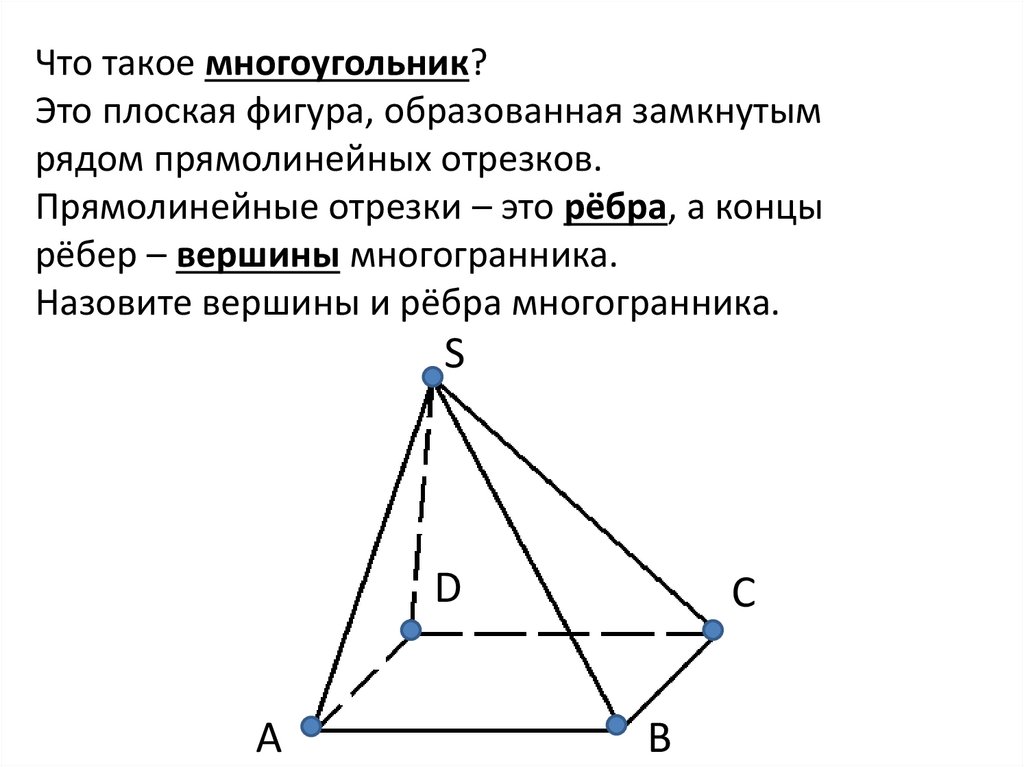
Что такое многоугольник?
Это плоская фигура, образованная замкнутым
рядом прямолинейных отрезков.
Прямолинейные отрезки – это рёбра, а концы
рёбер – вершины многогранника.
Назовите вершины и рёбра многогранника.
S
D
A
C
B

13.

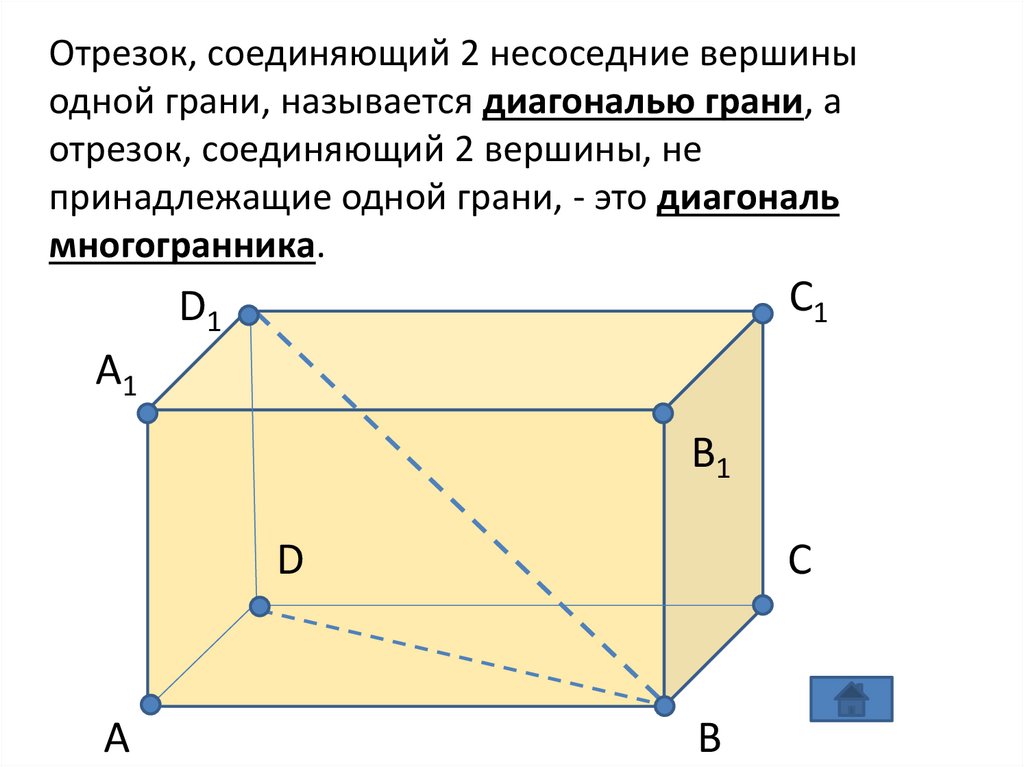
Отрезок, соединяющий 2 несоседние вершины
одной грани, называется диагональю грани, а
отрезок, соединяющий 2 вершины, не
принадлежащие одной грани, - это диагональ
многогранника.
C1
D1
A1
B1
D
A
C
B

14.

Характеристика Эйлера
Равенство, которое выражает Эйлерову
характеристику, было им доказано в 1752
году.
Если характеристика Эйлера равна 2, то это
выпуклый многогранник.
Вычисляется характеристика Эйлера
следующим образом:
В – Р + Г, где В – число вершин, Р – число
рёбер, Г – число граней.

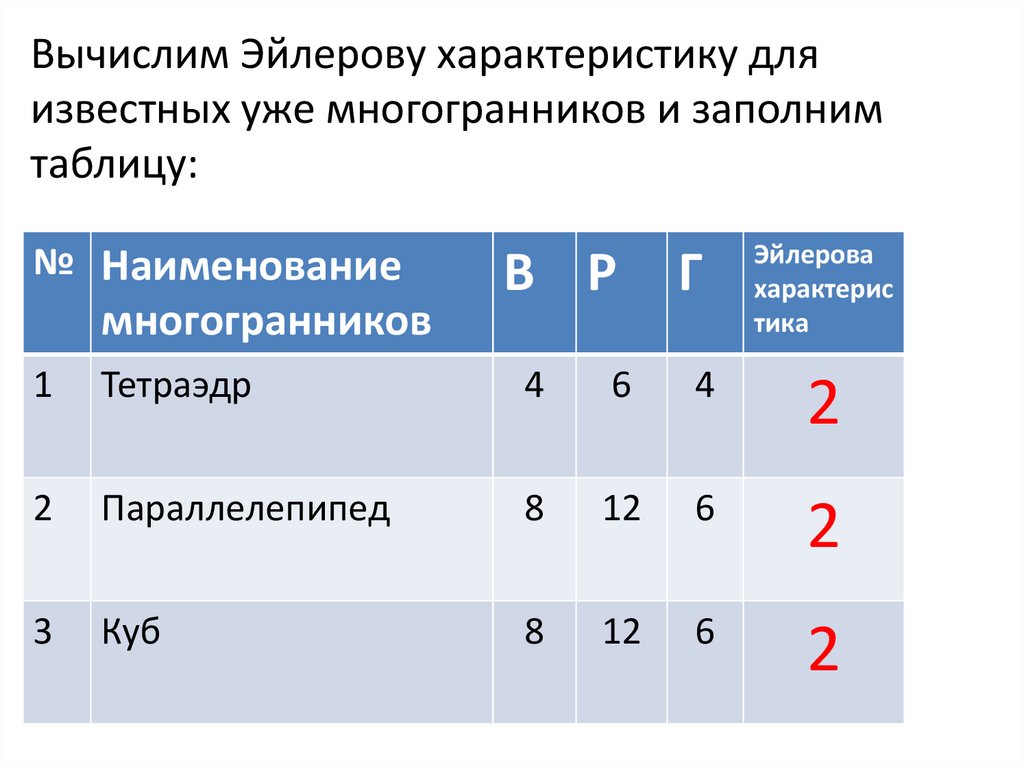
15.

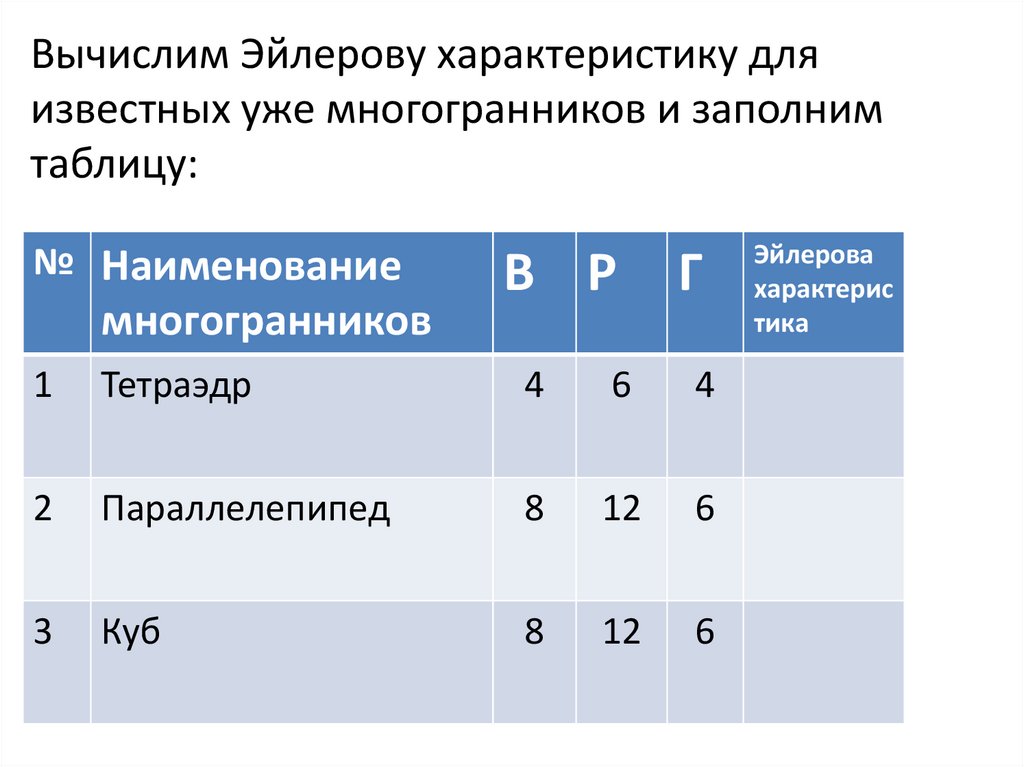
Вычислим Эйлерову характеристику для
известных уже многогранников и заполним
таблицу:
№ Наименование
многогранников
В Р
Г
1
Тетраэдр
4
6
4
2
Параллелепипед
8
12
6
3
Куб
8
12
6
Эйлерова
характерис
тика

16.

Вычислим Эйлерову характеристику для
известных уже многогранников и заполним
таблицу:
№ Наименование
многогранников
В Р
Г
Эйлерова
характерис
тика
1
Тетраэдр
4
6
4
2
2
Параллелепипед
8
12
6
2
3
Куб
8
12
6
2

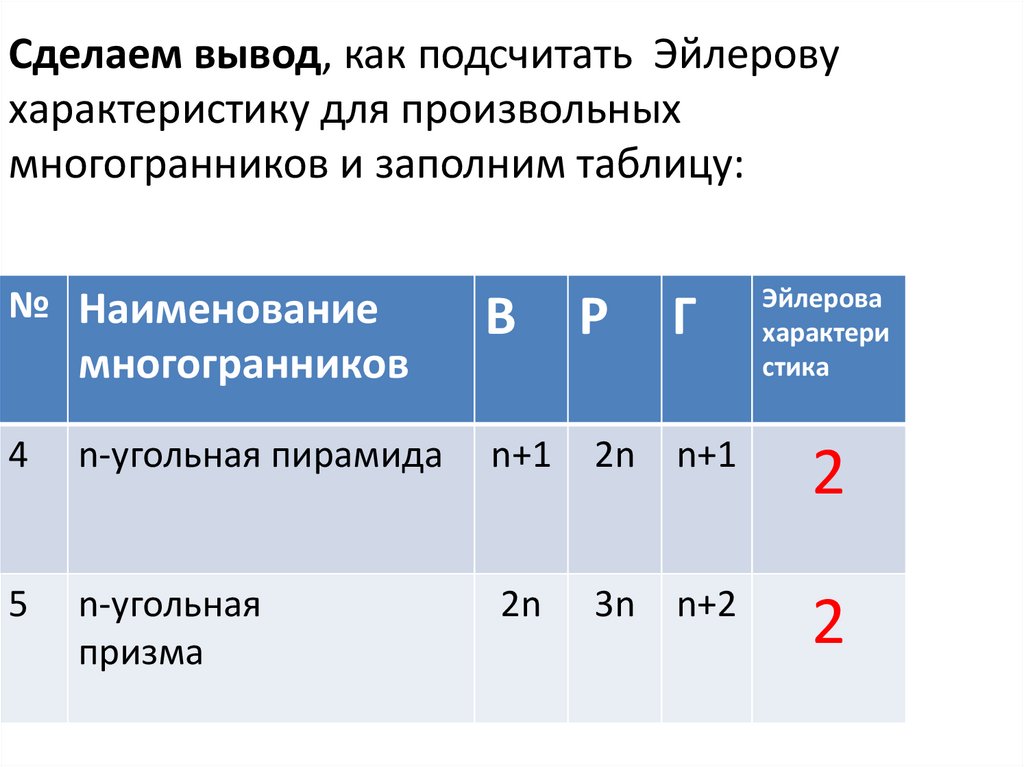
17.

Сделаем вывод, как подсчитать Эйлерову
характеристику для произвольных
многогранников и заполним таблицу:
№ Наименование
многогранников
В
Р
Г
Эйлерова
характери
стика
4
n-угольная пирамида
n+1
2n
n+1
2
5
n-угольная
призма
2n
3n
n+2
2

18.

Многогранник называется выпуклым,
если он расположен по одну сторону от
плоскости каждой его грани.
В противном случае – это невыпуклый
многогранник.
Теорема.
В любом многограннике сумма всех
плоских углов при каждой вершине
меньше 360°.

19.

Призма.
Задание классу:
К следующему уроку подготовить
презентацию «Призма» (пункт 27).

20.

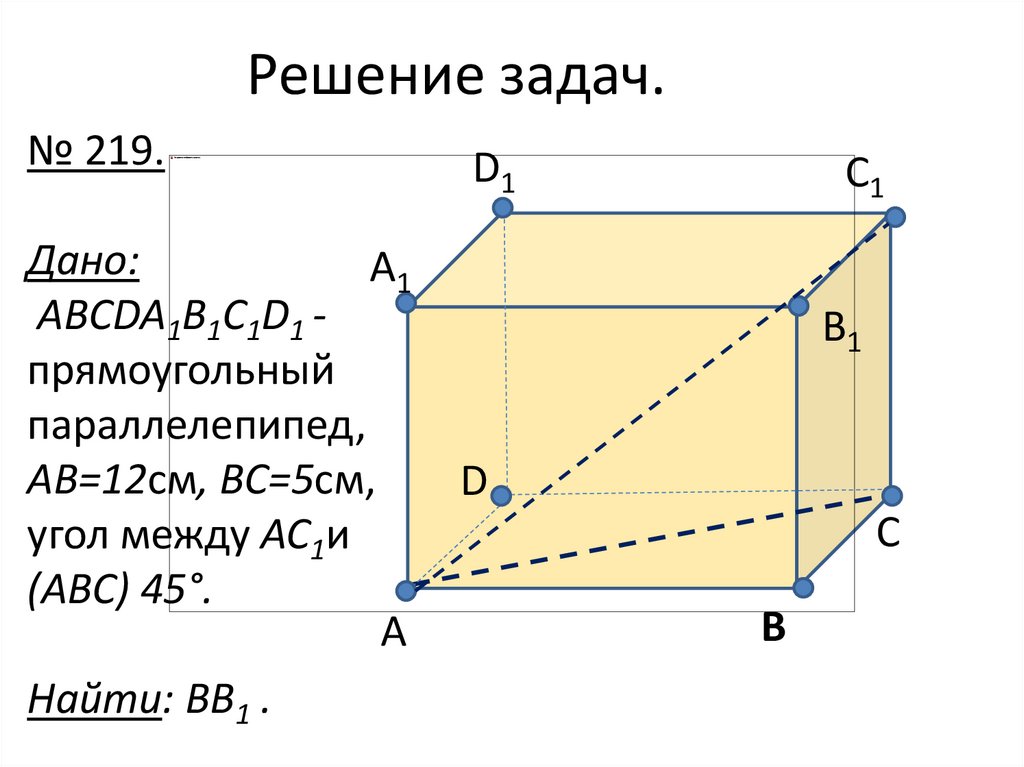
Решение задач.
Задание классу: № 219, 223

21.

Решение задач.
№ 219.
Дано:
A1
ABCDA1B1C1D1 прямоугольный
параллелепипед,
AB=12см, BC=5см,
угол между AC1и
(ABC) 45°.
A
Найти: BB1 .
D1
C1
B1
D
C
B

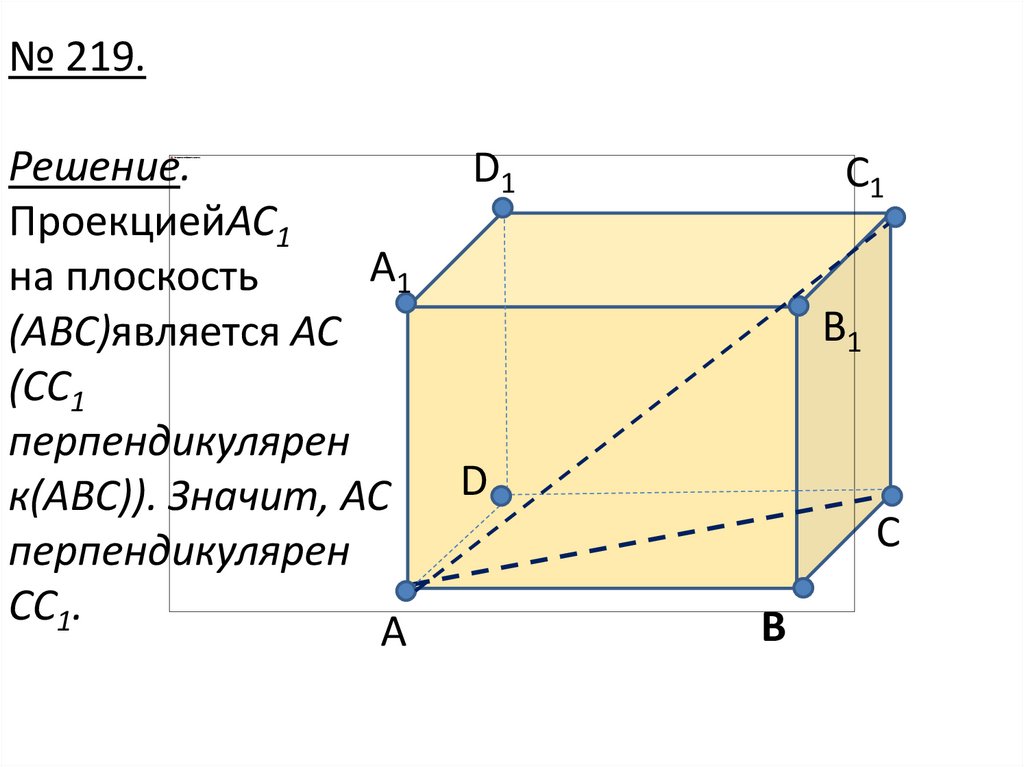
22.

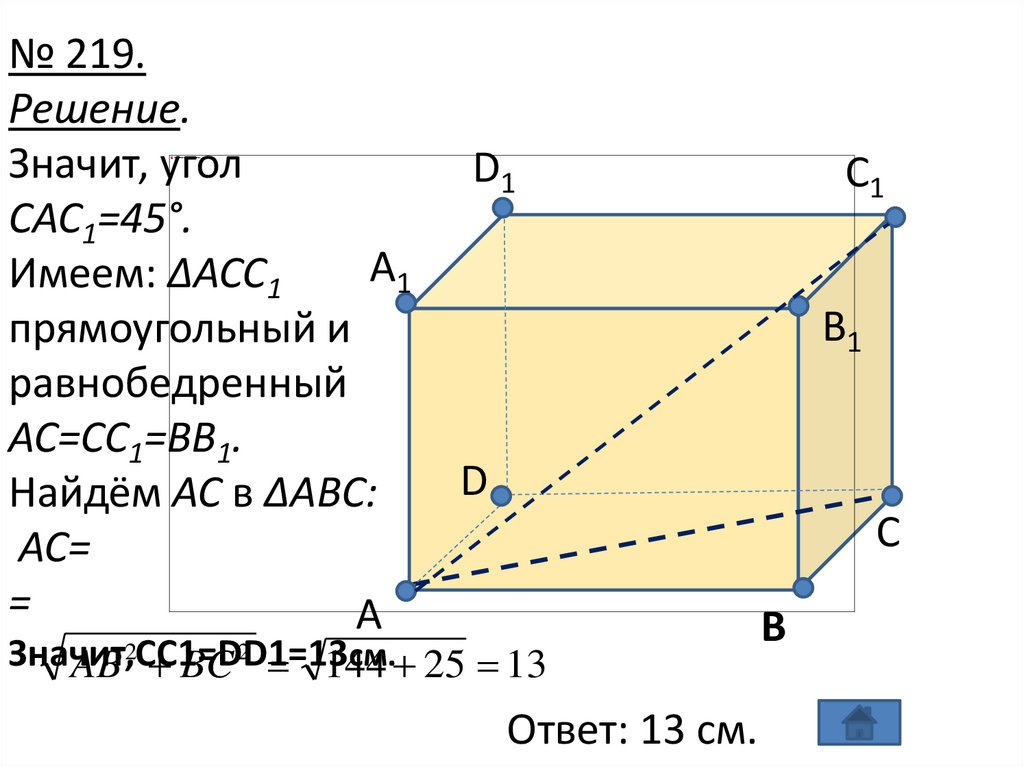
№ 219.
Решение.
ПроекциейAC1
A1
на плоскость
(ABC)является AC
(CC1
перпендикулярен
к(ABC)). Значит, AC
перпендикулярен
CC1.
A
D1
C1
B1
D
C
B

23.

№ 219.
Решение.
Значит, угол
CAC1=45°.
A1
Имеем: ΔACC1
прямоугольный и
равнобедренный
AC=CC1=BB1.
Найдём AC в ΔABC:
AC=
=
A
D1
B1
D
C
Значит,CC1=DD1=13
см. 25 13
AB BC 144
2
C1
2
Ответ: 13 см.
B

24.

Домашнее задание.
Задание классу:
Пункты 25-27, № 220.

25.

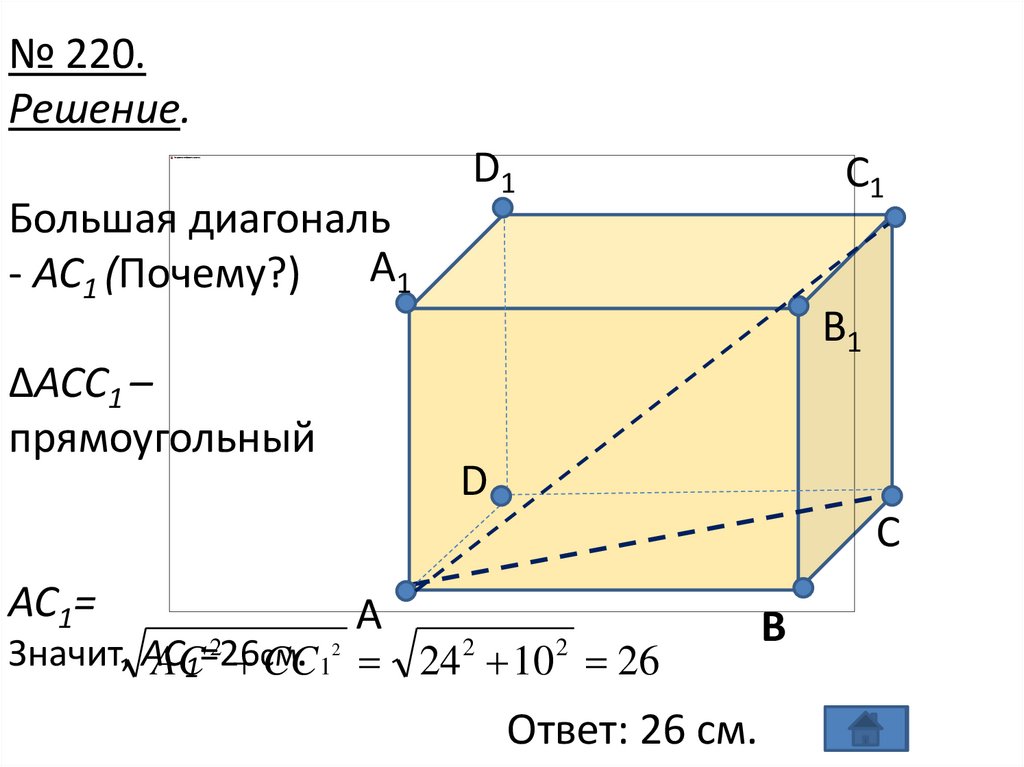
№ 220.
Решение.
Большая диагональ
- AC1 (Почему?) A1
D1
C1
B1
ΔACC1 –
прямоугольный
D
C
AC1=
A
Значит, AC
AC1=26
см.
CC1 24 10 26
2
2
2
2
Ответ: 26 см.
B