Взаимное расположение прямых в пространстве

1.

Урок №4
Взаимное расположение
прямых в пространстве

2.

Цели обучения
• 10.2.2 - знать определение параллельных и
скрещивающихся прямых в пространстве,
определять и изображать их;

3.

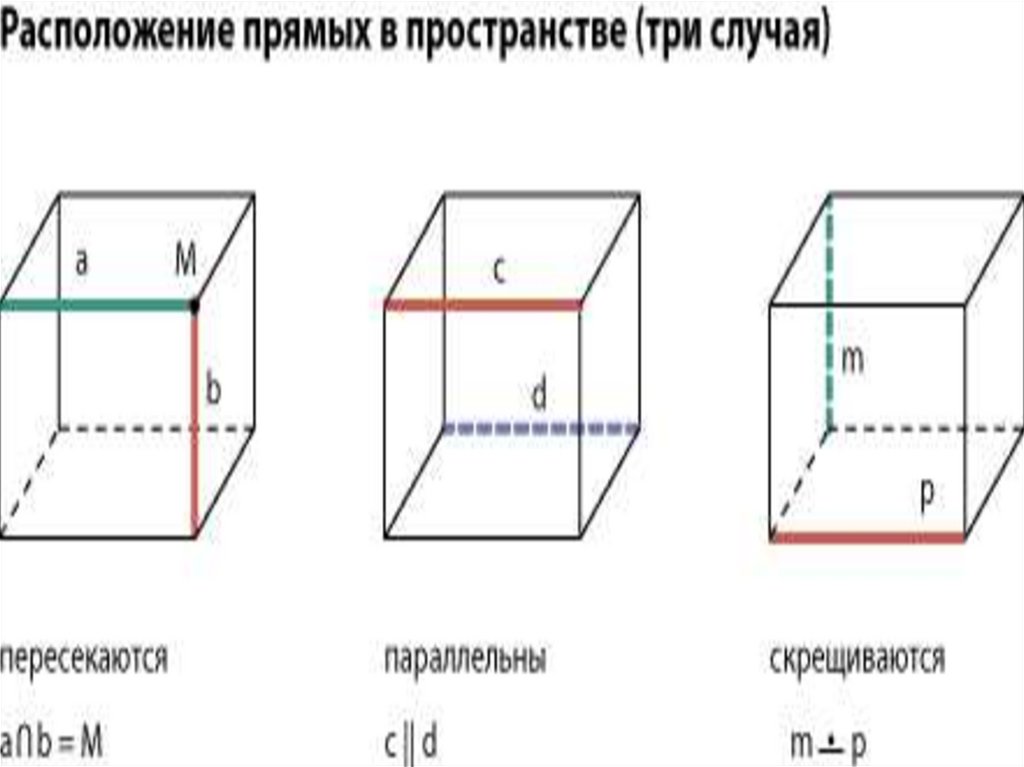
Что объединяет картинки?

4.

Что объединяет картинки?

5.

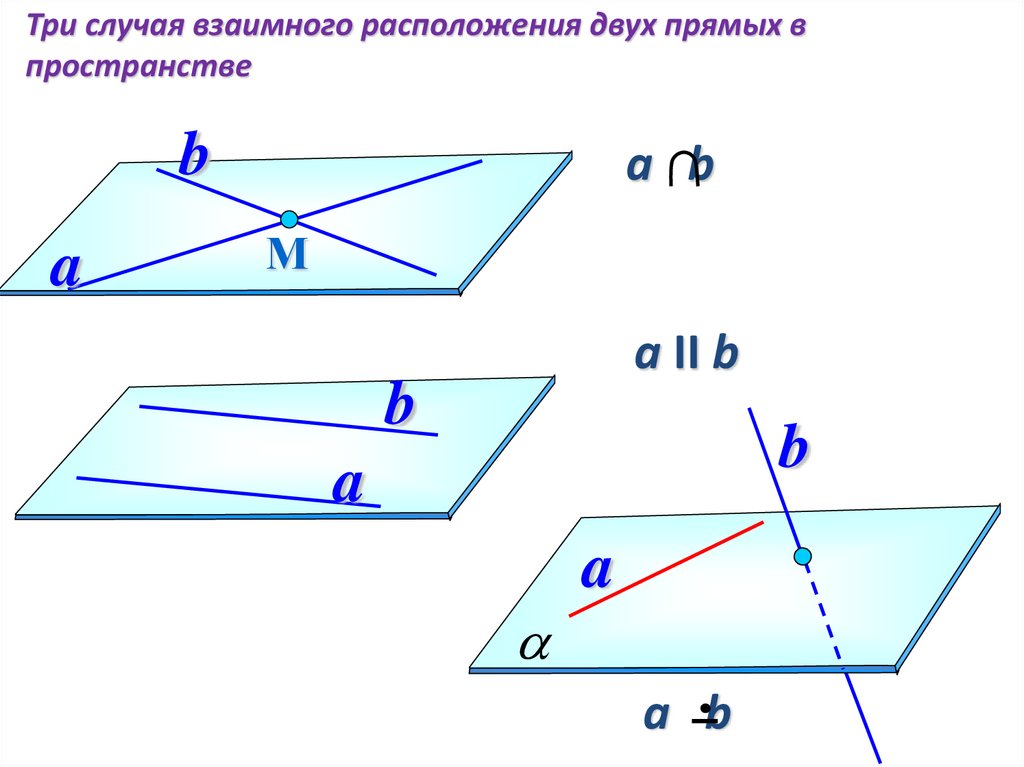
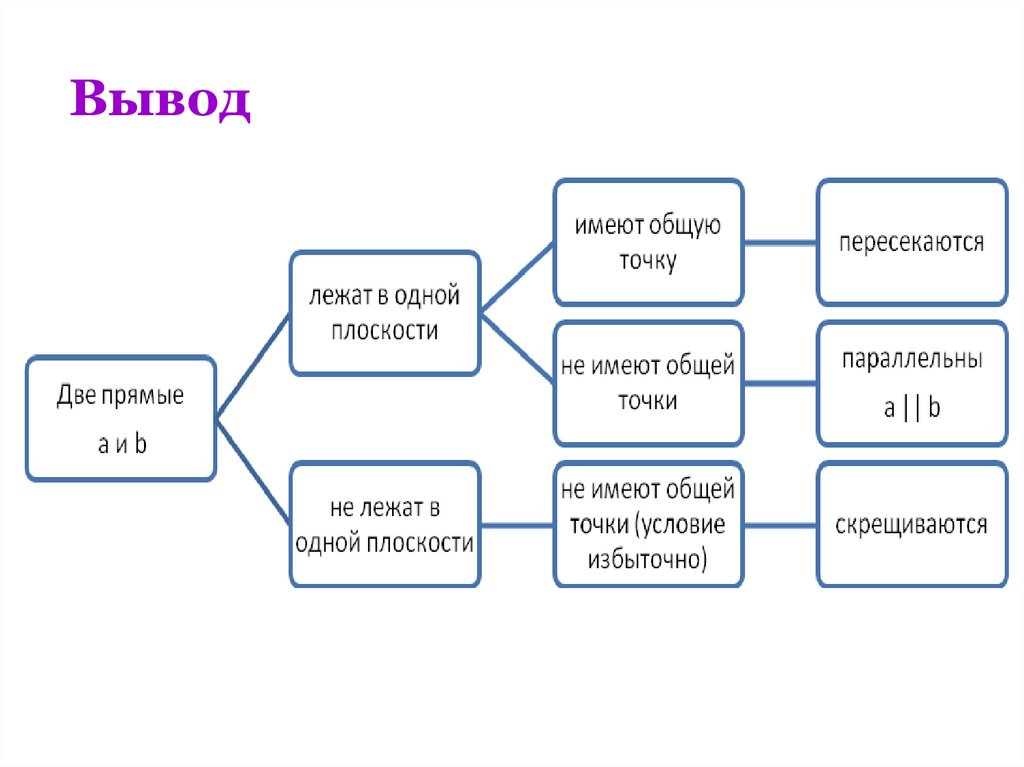
Три случая взаимного расположения двух прямых в
пространстве
b
a
а b
М
а II b
b
b
a
a
а b

6.

7.

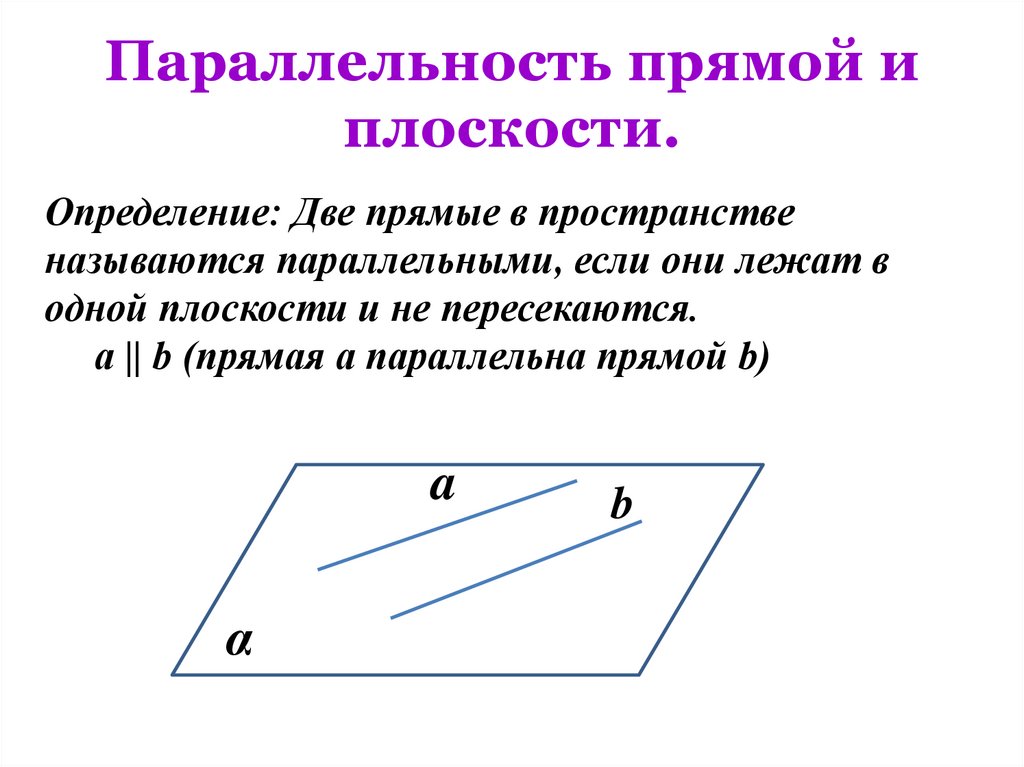
Параллельность прямой и
плоскости.
Определение: Две прямые в пространстве
называются параллельными, если они лежат в
одной плоскости и не пересекаются.
a || b (прямая а параллельна прямой b)
a
α
b

8.

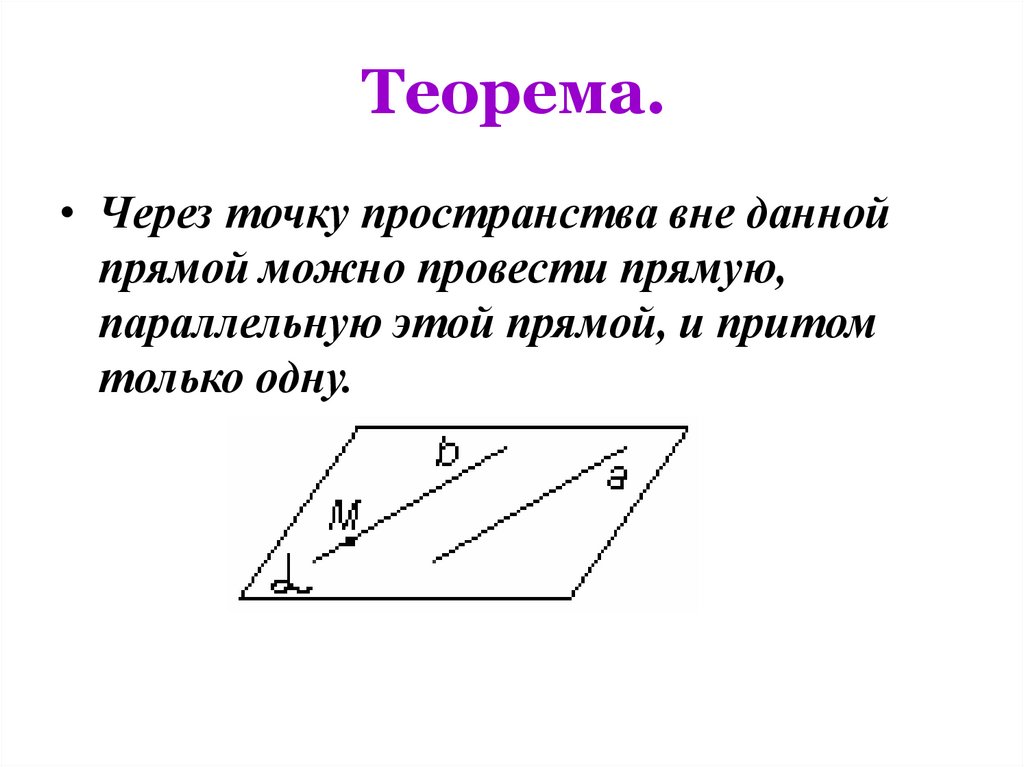
Теорема.
• Через точку пространства вне данной
прямой можно провести прямую,
параллельную этой прямой, и притом
только одну.

9.

Теорема.
• Если две прямые параллельны третьей
прямой, то они параллельны.

10.

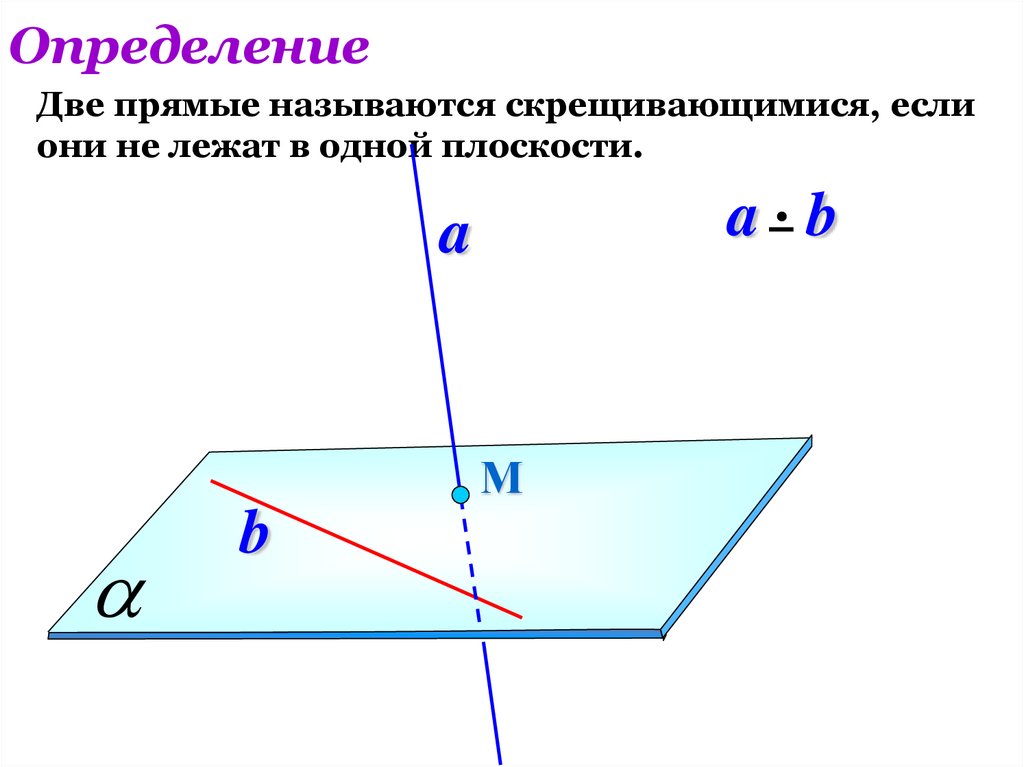
Определение
Две прямые называются скрещивающимися, если
они не лежат в одной плоскости.
a b
a
М
b

11.

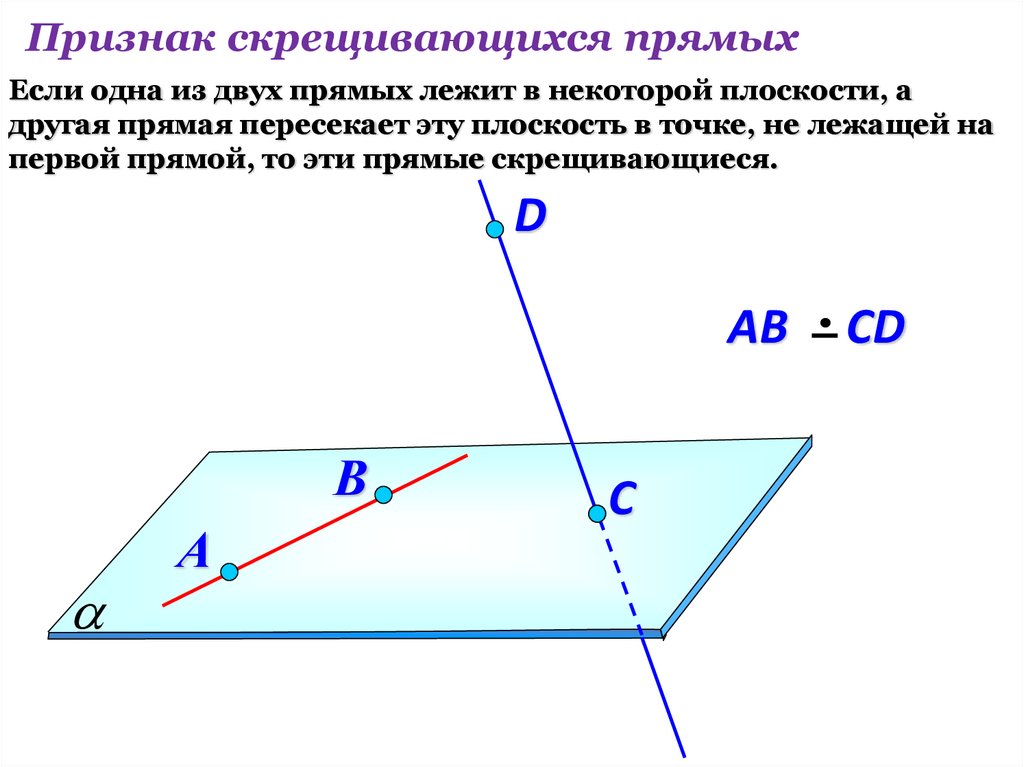
Признак скрещивающихся прямых
Если одна из двух прямых лежит в некоторой плоскости, а
другая прямая пересекает эту плоскость в точке, не лежащей на
первой прямой, то эти прямые скрещивающиеся.
D
АВ
В
А
C
СD

12.

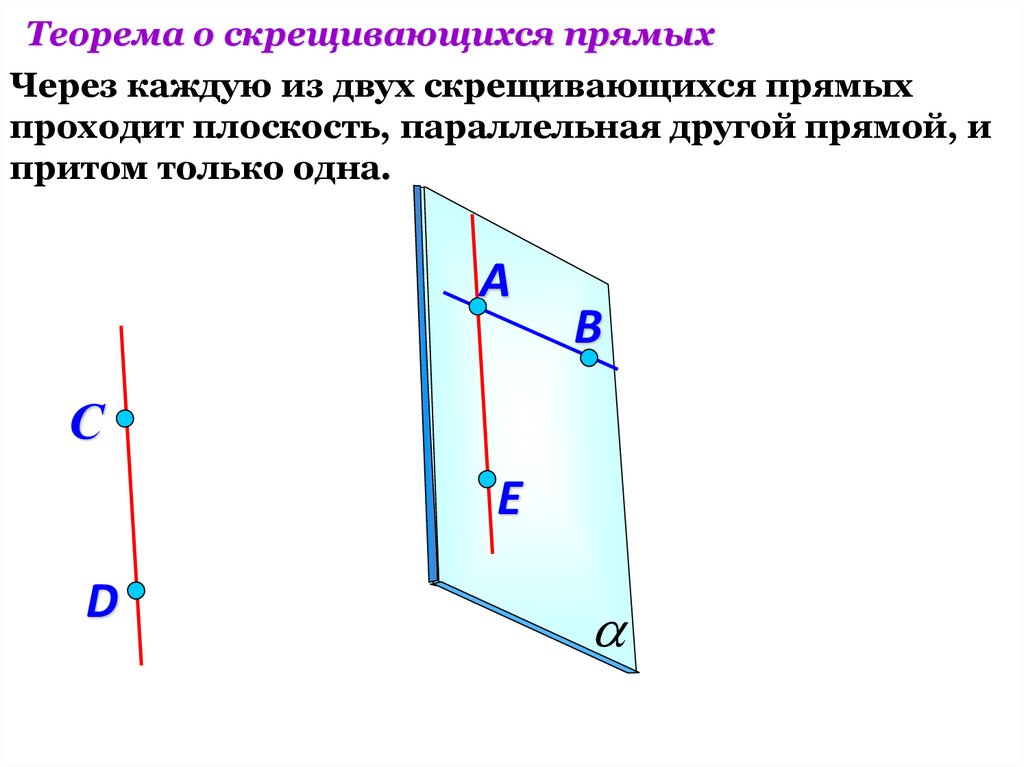
Теорема о скрещивающихся прямых
Через каждую из двух скрещивающихся прямых
проходит плоскость, параллельная другой прямой, и
притом только одна.
A
B
С
E
D

13.

Вывод

14.

Рефлексия