Электростатика. Лекция 1. Физика. 2 курс

1.

Физика. 2 курс. 3 семестр
Лекция 1. Электростатика
В.И. Читайкин
кандидат физико-математических наук
доцент
специалитет

2.

Мои поздравления Вам, студентам, прошедшим через горнило
первого года обучения в химико-технологическом
университете имени Дмитрия Ивановича Менделеева!
Пусть уверенности в своих силах Вам придаёт понимание
того, что этот тернистый путь уже прошли более ста
поколений студентов. Значит, пройдёте и Вы!
Успехов!
2

3.

План лекции
Наименование раздела
Номер
слайда
Введение
4
Раздел 1. Основные положения электростатики
(экспериментальный базис)
6
Раздел 2. Напряжённость электрического поля
10
Раздел 3. Теорема Остроградского-Гаусса
14
3

4.

Введение
Общие замечания
Курс физики для студентов 2-ого курса, 3-его семестра, весьма объёмен.
Он включает в себя все практически важные разделы электромагнетизма и ряд
смежных разделов:
- электростатика и магнетизм,
- законы электрических цепей и оптических явлений,
- тепловое излучение
- и, конечно, уравнения электромагнитного поля (уравнения Максвелла) как вершина
электромагнетизма и теоретическая основа всех его приложений.
Изучение этого курса потребует усилий, но преодоление трудностей, безусловно,
сделает Вашу учёбу яркой и интересной.
4

5.

Введение
Об учебниках
1. Трофимова Таисия Ивановна, «Курс физики», любое издание после 2005
года. Обязательный учебник.
2. Иродов Игорь Евгеньевич, «Электромагнетизм. Основные законы»,
любые издания после 2010 года Любителям красивой физики, чёткой и
прозрачной.
3. Савельев Игорь Владимирович, «Курс физики», том 2, любые издания
после 2010 года. Любителям глубоко поразмышлять.
5

6.

Раздел 1. Основные положения электростатики
(экспериментальный базис)
6

7.

1. Основные положения (экспериментальный базис)
Электростатика – это наука, изучающая взаимодействие и свойства систем неподвижных
электрических зарядов. Электростатика, как и другие разделы физики, базируется на опытных данных.
Экспериментально установлено:
- в природе существуют два типа электрических зарядов: положительные и отрицательные;
- одноимённые электрические заряды отталкиваются, разноимённые – притягиваются;
элементарный (наименьший) электрический заряд равен q = 1,6∙10-19 Кл (Кулон (Кл) – единица
измерения электрического заряда);
- существуют материальные частицы-носители элементарного заряда:
- протон (p или p+) – носитель положительного элементарного заряда:
электрический заряд протона qp+ = + 1,6∙10-19 Кл, масса протона mp+ = 1,7∙10-27 кг;
- электрон (e или e-) – носитель отрицательного элементарного заряда:
электрический заряд электрона qe- = - 1,6∙10-19 Кл, масса электрона me- = 9,0∙10-31 кг.
Эти электрические и массовые параметры материальных частиц-носителей элементарного
электрического заряда определяют строение атомов, их основные закономерности, т.е. в
конечном итоге, структуру таблицы Менделеева.
7

8.

1. Основные положения (экспериментальный базис)
В результате обобщения результатов длительных наблюдений и экспериментов был установлен
закон сохранения электрического заряда (М.Фарадей, XIX век): алгебраическая сумма электрических
зарядов частиц или тел, образующих электрически изолированную систему, не изменяется при любых
процессах, происходящих в этой системе.
qi – электрический заряд i-ого тела (частицы) в электрически изолированной системе, содержащей n
тел (частиц).
Например, при трении двух первоначально электрически нейтральных тел друг о друга
электрические заряды переходят от одного тела к другому, заряжая их, но суммарный электрический
заряд двух тел остаётся неизменным, каким он был до взаимодействия, т.е. нулевым.
Другой пример, при ионизации или диссоциации первоначально электрически нейтрального тела
или среды образуется одинаковое количество положительно заряженных ионов и отрицательно
заряженных электронов. Суммарный электрический заряд не меняется.
8

9.

1. Основные положения (экспериментальный базис)
Также в результате обобщения результатов длительных наблюдений и экспериментов был
установлен закон Кулона (закон взаимодействия электрических зарядов друг с другом):
Сила взаимодействия F между двумя неподвижными точечными зарядами q1 и q2 равна
произведению этих зарядов, обратно пропорциональна квадрату расстояния между ними r и
направлена по прямой, соединяющей эти заряды.
|F21| = |F12|
-
коэффициент пропорциональности
ε0 = 8,85∙10-12 Кл2/Н∙м – электрическая постоянная
ε - диэлектрическая проницаемость среды между зарядами – показатель
ослабления силы взаимодействия между электрическими зарядами по
сравнению в вакуумом (парафин ε = 2, фарфор ε = 5, вода ε = 81)
9

10.

Раздел 2. Напряжённость электрического поля
10

11.

2. Напряжённость электрического поля
Электрически заряженные частицы (тела) создают вокруг себя электрическое поле, посредством
которого такие частицы (тела) воздействуют друг на друга, находясь на определённом расстоянии,
т.е. не вступая в непосредственный контакт. Это взаимодействие называется кулоновским, сила
такого взаимодействия определяется законом Кулона.
Основная характеристика электрического поля, создаваемого электрическим зарядом q, - это
напряжённость Е.
Определение: напряжённость Е есть отношение силы Кулона F, действующей между зарядом q
и так называемым «пробным зарядом» qпр, размещённым на расстоянии r от заряда q, к величине
этого пробного заряда qпр.
r – расстояние между зарядами q и qпр.
Обратите внимание: напряжённость Е не зависит от
величины «пробного» заряда qпр.
Напряжённость Е векторная величина. Для точечного заряда q
линии напряжённости расходятся в виде лучей во все стороны.
Для положительного заряда линии выходят из него,
для отрицательного заряда – входят.
11

12.

2. Напряжённость электрического поля
Сила воздействия электрического поля на заряд, находящегося в этом поле.
(Внимание: на рисунке используются иные обозначения некоторых параметров!)
Заряд Q создаёт электрического поле напряжённостью Е:
На расстоянии d от источника (заряд Q) помещён заряд q.
Сила, с которой поле Е действует на заряд q, определяется так:
Проверка: подставив в эту формулу выражение для Е, получим силу Кулона:
Как и должно было быть!
12

13.

2. Напряжённость электрического поля
Принцип суперпозиции электрических полей
Электрическое поле в точке А создаётся двумя зарядами
q1 > 0 и q2 < 0 (рисунок). Векторы напряжённости поля от
каждого заряда (Е1 и Е2) направлены по прямой,
соединяющей точку А с зарядами q1 и q2, соответственно.
Суммарная напряжённость электрического поля точке А
равна векторной сумме: Е = Е1 + Е2.
Принцип суперпозиции электрических полей: если электрическое поле в заданной точке
пространства создаётся n зарядами, то суммарная напряжённость поля Е рассчитывается как
векторная сумма напряжённостей от каждого заряда в отдельности Еi.
Самостоятельно: вывести данное уравнение из
принципа суперпозиции сил, действующих на
тело (использовать закон Кулона и раздел
«Механика»).
13

14.

Раздел 3. Теорема Остроградского-Гаусса
14

15.

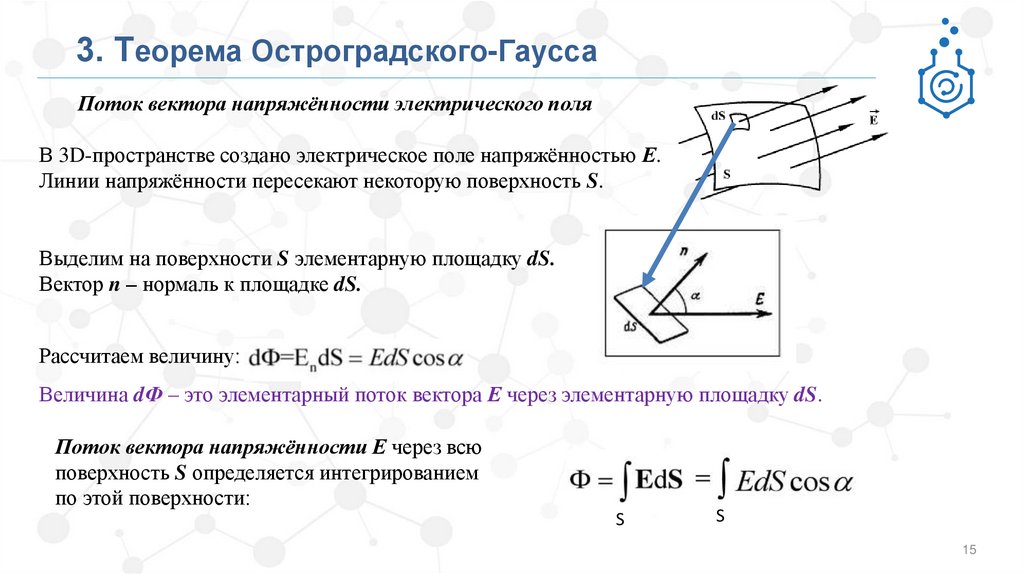
3. Теорема Остроградского-Гаусса
Поток вектора напряжённости электрического поля
В 3D-пространстве создано электрическое поле напряжённостью Е.
Линии напряжённости пересекают некоторую поверхность S.
Выделим на поверхности S элементарную площадку dS.
Вектор n – нормаль к площадке dS.
Рассчитаем величину:
Величина dФ – это элементарный поток вектора Е через элементарную площадку dS.
Поток вектора напряжённости Е через всю
поверхность S определяется интегрированием
по этой поверхности:
S
S
15

16.

3. Теорема Остроградского-Гаусса
Теорема Остроградского-Гаусса: поток вектора напряжённости электрического поля Е через
произвольную замкнутую поверхность S равен алгебраической сумме электрических зарядов,
охватываемых этой поверхностью.
Линии напряжённости от положительных зарядов «вытекают» через
поверхность S (не показано, дорисуйте сами);
Линии напряжённости от отрицательных зарядов «втекают» внутрь
поверхности S (не показано, дорисуйте сами).
Полный поток вектора напряжённости электрического поля Е через всю поверхность S составит
в вакууме:
ʃ
Самостоятельно: написать формулу для потока
Ф в среде с диэлектрической постоянной ε.
S
16

17.

3. Теорема Остроградского-Гаусса
Теорема Остроградского-Гаусса позволяет рассчитывать электрические поля,
созданными как отдельными зарядами, так и их совокупностью.
Наиболее просто можно выполнить расчёты для электрически заряженных тел,
обладающих симметрией: точечной, плоской, цилиндрической, сферической. В этих
случаях значение интеграла, входящего в формулу теоремы Остроградского-Гаусса:
ʃ
S
легко вычисляется в аналитическом виде.
Конкретные примеры таких вычислений будут рассмотрены на семинарских занятиях.
17

18.

Спасибо за внимание