Similar presentations:
Обратное распространение ошибки
1.
Обратноераспространение
ошибки
Корлякова М.О.
2019
2.
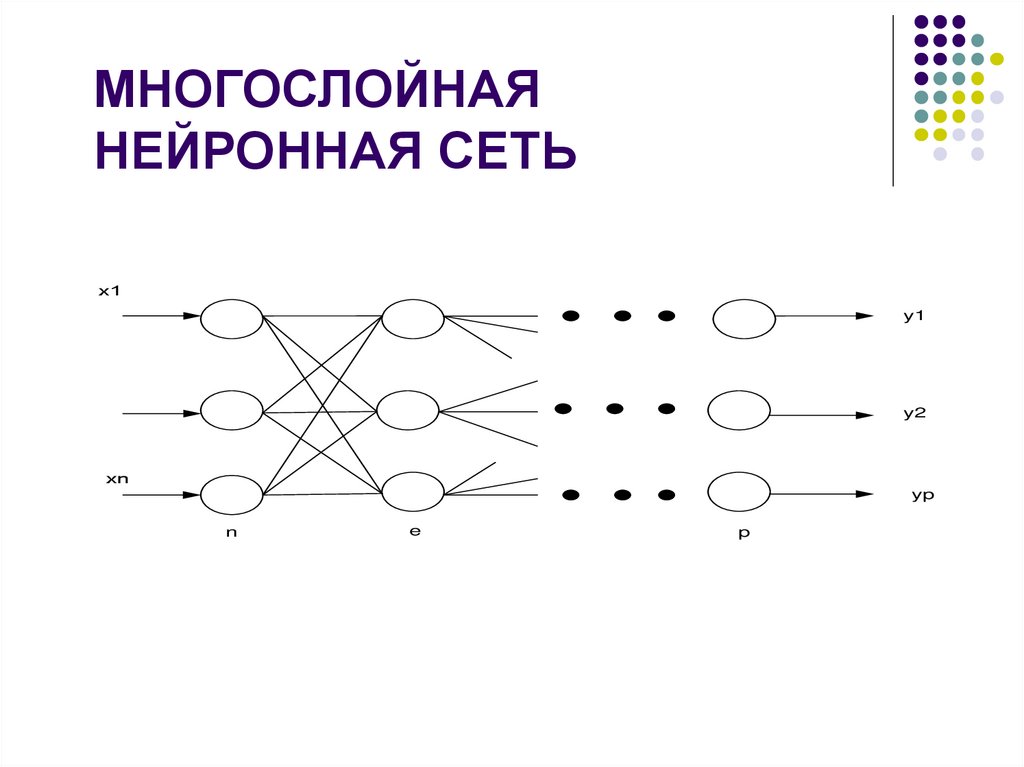
МНОГОСЛОЙНАЯНЕЙРОННАЯ СЕТЬ
х1
y1
y2
хn
yp
n
e
p
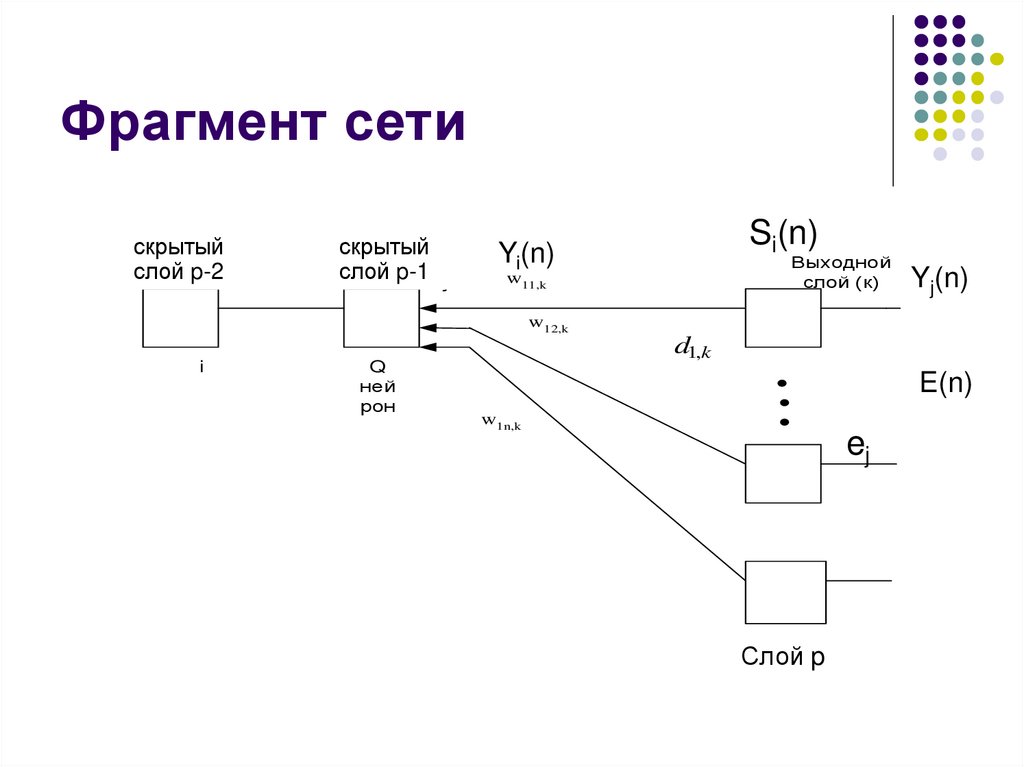
3.
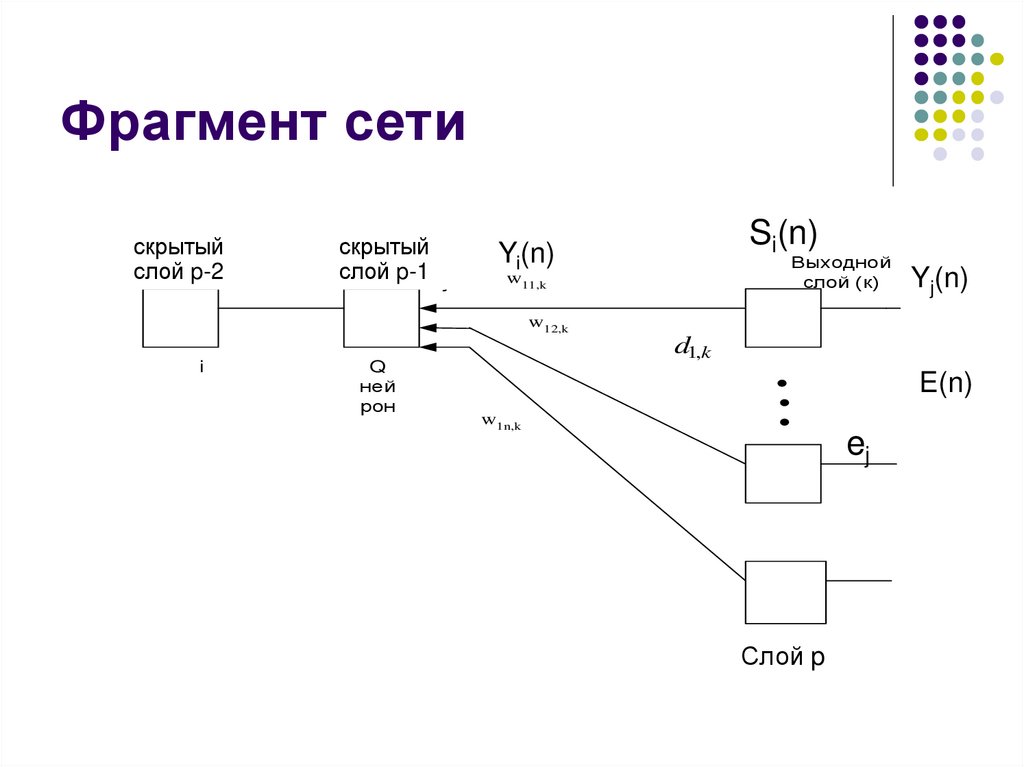
Фрагмент сетискрытый
Предварит
слой
p-2j-1
слой
скрытый
Скрытый
слой
p-1
слой j
Выходной
слой (к)
w11,k
Yj(n)
w12,k
OUT i
i
Si(n)
Yi(n)
Q
ней
рон
d1,k
E(n)
w1n,k
ej
Слой p
4.
Обучение по ошибкеГлобальная задача – сложная.
E(n)= ej(n)2
ej(n)=Dj-Yj(n)
Зависит от всех настраиваемых
параметров.
5.
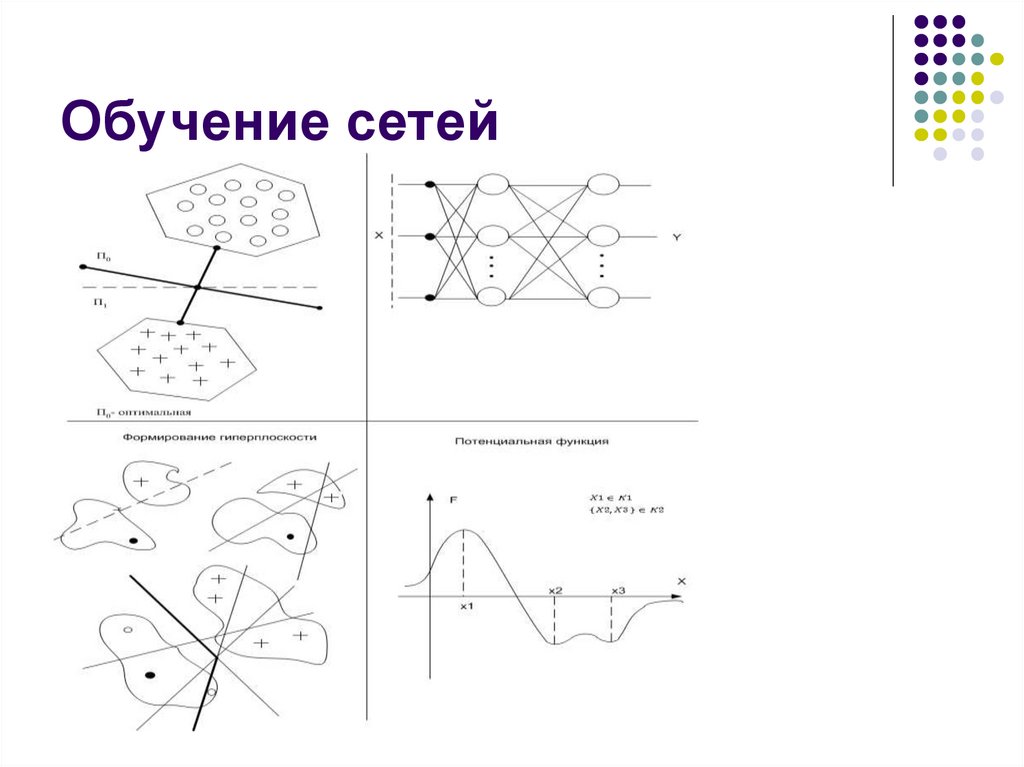
Обучение сетей6.
Обучение сетей прямогораспространения
Обучение перцептрона
Теорема Розенблата
Перцептрон можно научить всему, что он может
представить
Теорема Новикова
Если
D2
0, D step 2
7.
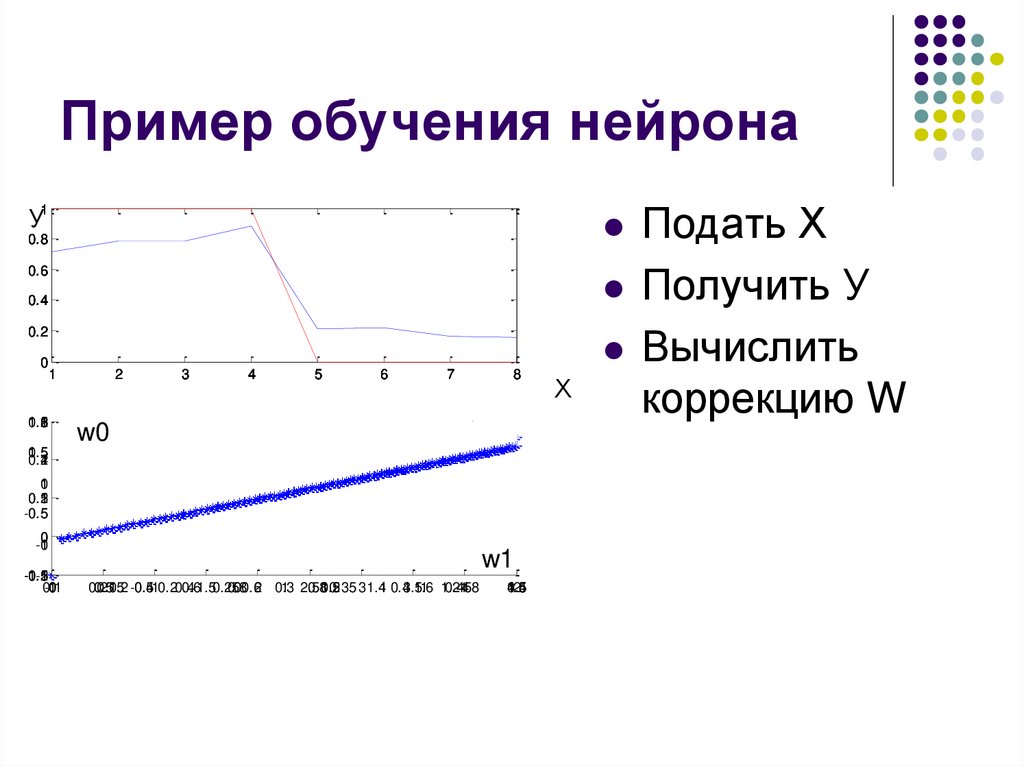
Пример обучения нейрона1
У
0.8
0.6
0.4
0.2
0
1
0.3
1.5
1
2
6
2
3
4
5
6
7
8
w0
1.5
0.5
0.2
1
4
0
1
0.5
0.1
2
-0.5
0.5
0
-1
0
-1.5
-0.1
-0.5
-2
0.1
-1
0
w1
0.2
0.5
0.15
0.2 -0.5
0.410.20.4
0.61.50.25
0.8
00.62 0.3
1 2.5
0.81.2
0.5
0.35 3 1.41 0.43.5
1.6
1 1.2
0.45
1.8
4
1.5
0.5
1.4
4.5
2
Х
Подать Х
Получить У
Вычислить
коррекцию W
8.
Обучение по ошибкеЛокальная задача – нет Dj для нейронов
скрытого слоя.
Обучение многократное.
Адаптируем синаптические веса по
ошибке.
Определим ejr(n) для нейронов скрытого
слоя r.
Зависит от настраиваемых параметров
только нейрона j в слое r.
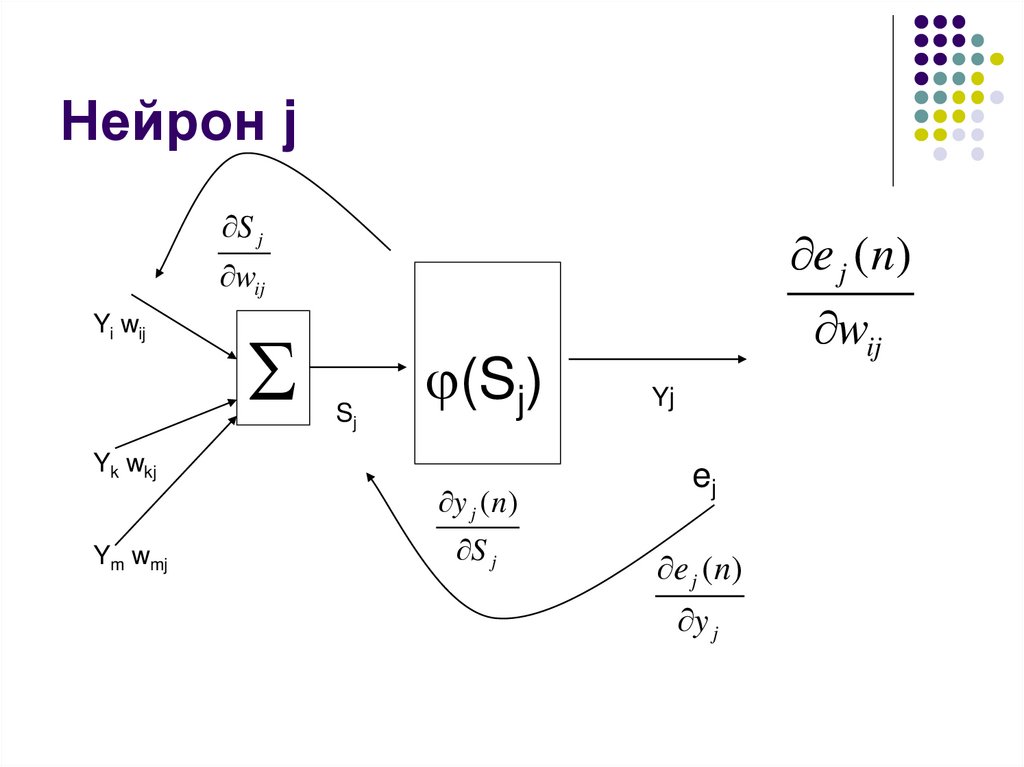
9.
Нейрон jS j
e j ( n)
wij
Yi wij
Yk wkj
Ym wmj
Sj
(Sj)
y j ( n)
S j
wij
Yj
ej
e j ( n)
y j
10.
Обратное распространение ошибкивыходной слой
E n E n e j n y j n S j n
wi j (n) e j (n) y j (n) S j (n) wi j (n)
1 k
E n e j ( n) 2
2 j 1
E n
e j (n) d j y j (n),
e j (n)
y j ( n) S j
y j n
S j (n)
S j (n) wi j yi (n)
e j n
y j (n)
1
( S j (n))
S j n
wi j (n)
yi (n)
E n
E n
e j (n) ( S j (n)) yi (n) wij (n)
wi j (n)
wi j (n)
11.
Фрагмент сетискрытый
Предварит
слой
p-2j-1
слой
скрытый
Скрытый
слой
p-1
слой j
Выходной
слой (к)
w11,k
Yj(n)
w12,k
OUT i
i
Si(n)
Yi(n)
Q
ней
рон
d1,k
E(n)
w1n,k
ej
Слой p
12.
Скрытый слой1
E (n) ek2 (n)
2 k
ek (n)
E (n)
ek
y j (n) k
y j (n)
ij (n)
e j
yi
e j (n) y j (n) S j (n)
y j (n) S j (n) yi
ei ek ik (n)
k
j ( S j (n)) wij
13.
Скрытый слойm
S k (n) wkj (n) y j (n)
j 0
S k (n)
wkj (n)
y j (n)
ek (n) S j (n)
E (n)
ek
y j (n) k
S j (n) y j (n)
ek (n) k ( S k (n)) wkj (n) k (n) wkj (n)
k
k
14.
Минимум потенциальнойэнергии
15.
ВопросПеречислите классы алгоритмов
обучения
К какому алгоритмов обучения относится
обучение многослойных сетей с
обратным распространением ошибки
16.
Функции пакета NeuralNetWork ToolBox MatLab
net = newff([0 8],[2 1],{'tansig' ‘purelin'},'trainlm');
net=train(net,p,t);
y2 = sim(net,p)
17.
АлгоритмыTRAINCGB
TRAINBFG
TRAINOSS
TRAINGD
TRAINRP
TRAINLM
18.
Neural Network objectarchitecture
numInputs: 1
numLayers: 2
biasConnect: [1; 1]
inputConnect: [1; 0]
layerConnect: [0 0; 1 0]
outputConnect: [0 1]
targetConnect: [0 1]
19.
numOutputs: 1 (read-only)numTargets: 1 (read-only)
numInputDelays: 0 (read-only)
numLayerDelays: 0 (read-only)
20.
subobject structures:inputs: {1x1 cell} of inputs
layers: {2x1 cell} of layers
outputs: {1x2 cell} containing 1 output
targets: {1x2 cell} containing 1 target
biases: {2x1 cell} containing 2 biases
inputWeights: {2x1 cell} containing 1 input weight
layerWeights: {2x2 cell} containing 1 layer weight
21.
functions:adaptFcn: 'trains'
initFcn: 'initlay'
performFcn: 'mse'
trainFcn: 'trainlm'
22.
trainParam:.epochs,
.goal,
.show,
.time
23.
weight and bias values:IW: {2x1 cell} containing 1 input weight matrix
LW: {2x2 cell} containing 1 layer weight
matrix
b: {2x1 cell} containing 2 bias vectors
24.
Обучение сети3 – нелинейных нейрона, градиентный
алгоритм
Без
Обучения
Целевое
состояние
Обучение
25.
Обучение сети8 – нелинейных нейронов, градиентный
алгоритм
Без
Обучения
Целевое
состояние
Обучение
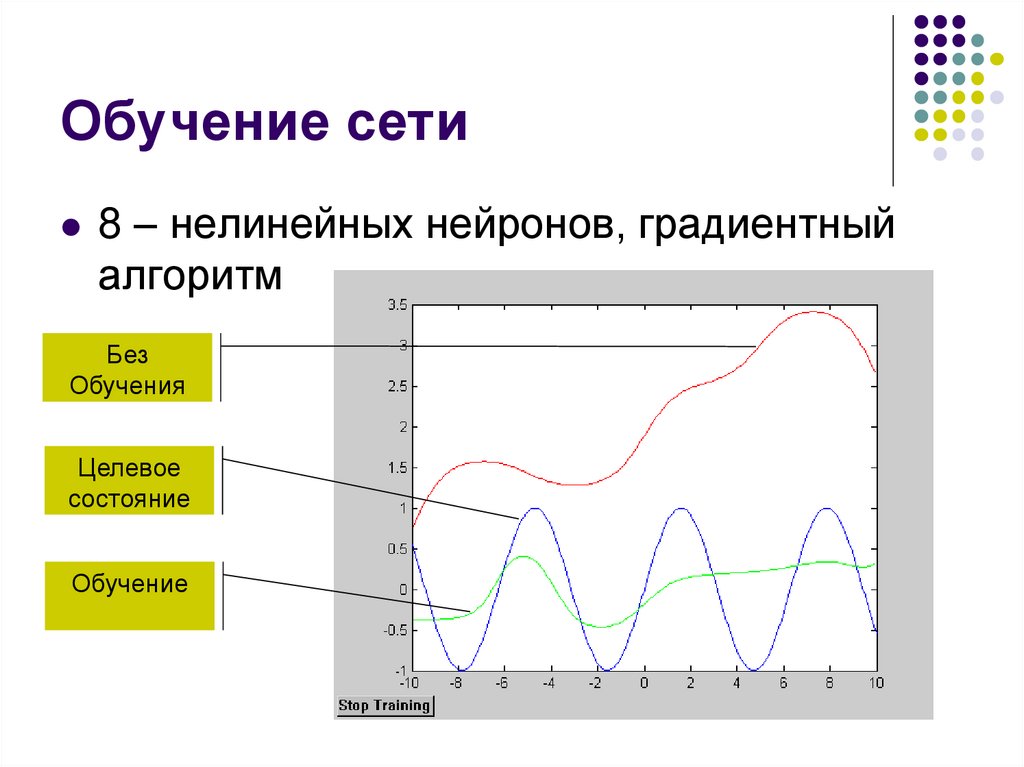
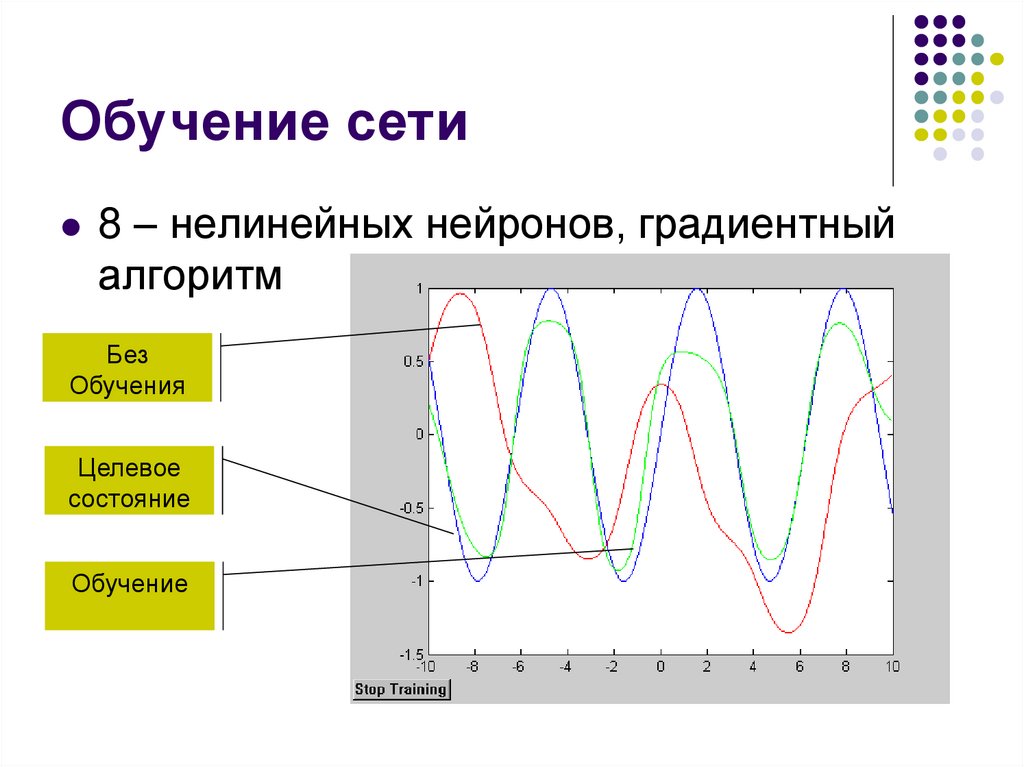
26.
Обучение сети8 – нелинейных нейронов, градиентный
алгоритм
Без
Обучения
Целевое
состояние
Обучение
27.
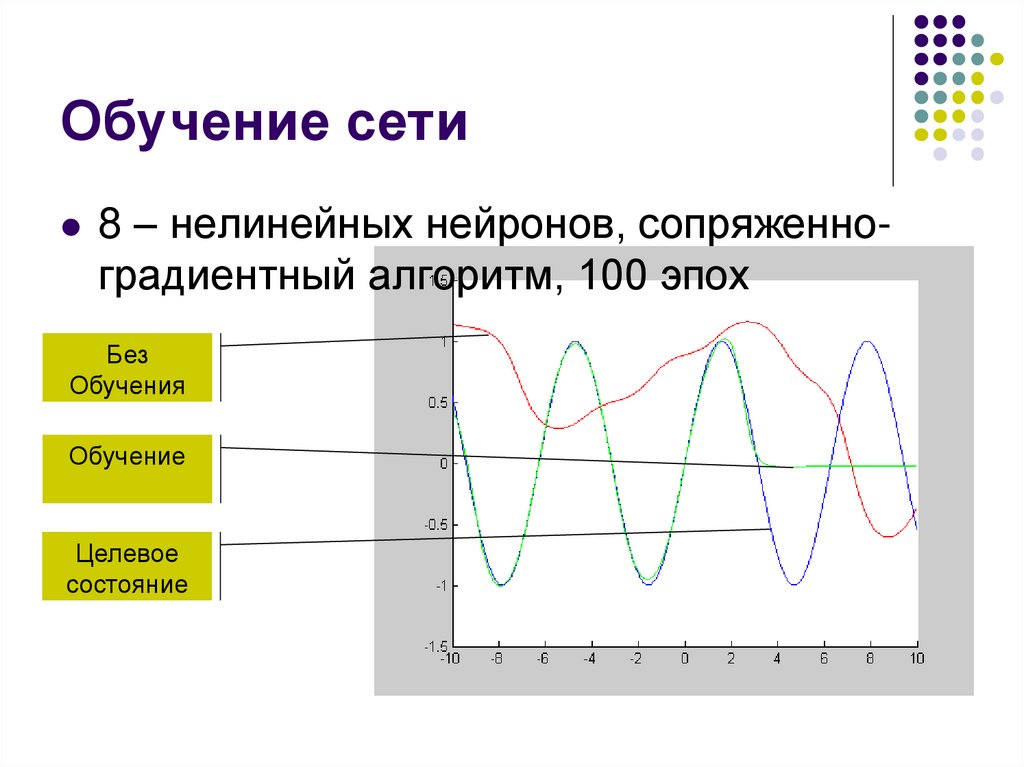
Обучение сети8 – нелинейных нейронов, сопряженноградиентный алгоритм, 100 эпох
Без
Обучения
Обучение
Целевое
состояние
28.
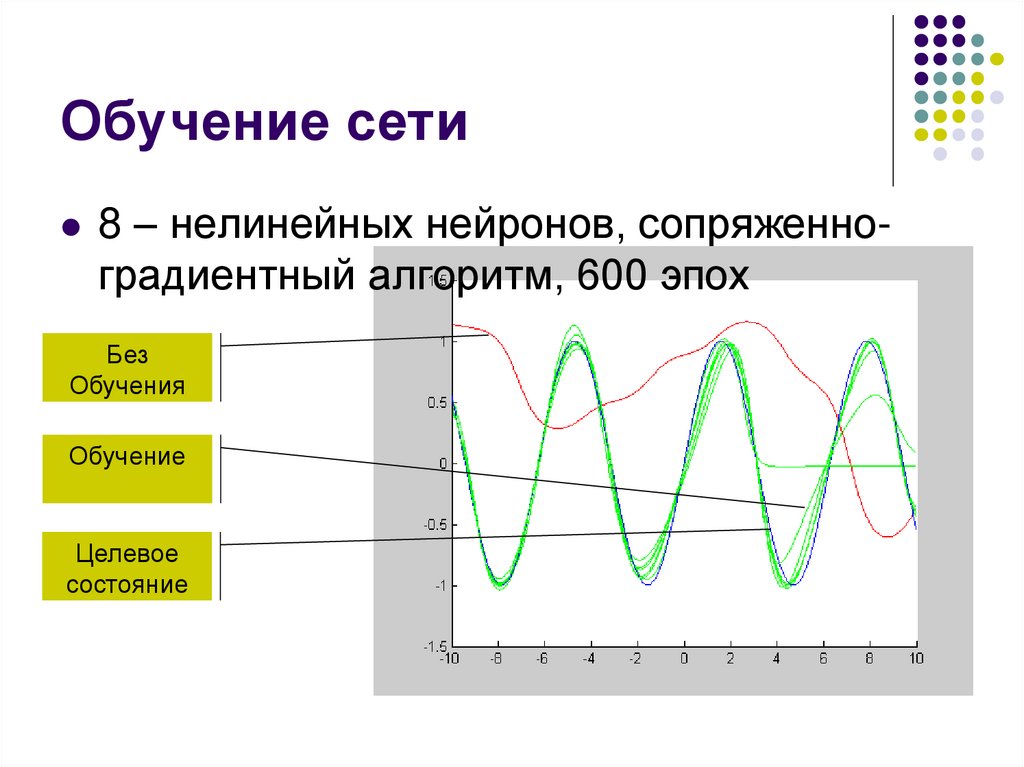
Обучение сети8 – нелинейных нейронов, сопряженноградиентный алгоритм, 600 эпох
Без
Обучения
Обучение
Целевое
состояние
29.
ПроблемыЛокальные минимумы
Переобучение
Паралич сети
Устойчивость/пластичность
30.
ВопросПриведите общую схему обучения
многослойной сети с обратным
распространением ошибки.




















 informatics
informatics








