Железобетонные балки. Лекция 3

1.

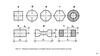
Рис.3.1. Напряженное состояние и схемы разрушения
железобетонной балки:
а – схема балки и эпюры изгибающих моментов и
поперечных сил;
б – траектории главных растягивающих напряжений и
схема образования трещин;
в – схема возможного разрушения балки;
г – сечение с одиночной арматурой;
д – сечение с двойным армированием;
1 – продольная арматура; 2 – отгибы; 3 – хомуты;
4 – монтажная арматура
3.1

2.

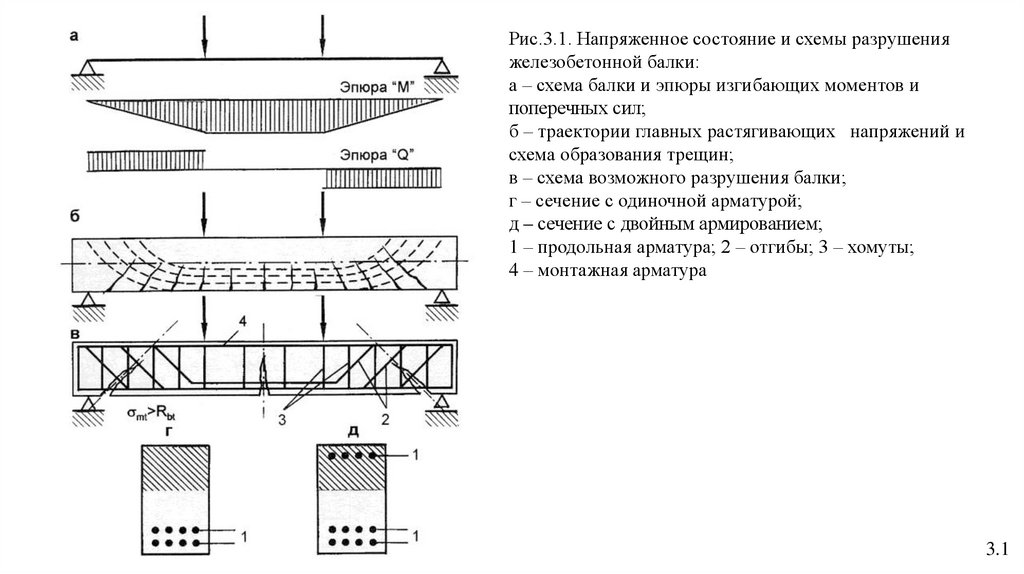
Рис.3.2. Стадии напряжено деформированного состояния
сечения железобетонной балки при изгибе
3.2

3.

M ≤ Mult,
(3.1)
где: M – расчетный изгибающий момент в данном
сечении, Mult – несущая способность сечения,
момент внутренних сил, обусловленный
сопротивлением бетона и арматуры.
RS AS - Rb b x = 0,
(3.2)
где: As - площадь поперечного сечения растянутой
арматуры; b - ширина сечения; x - высота сжатой
зоны бетона.
x = (RS AS)/( Rb b)
(3.3)
Рис. 3.3. Схема усилий в нормальном сечении
изгибаемого элемента с одиночной арматурой в стадии
предельного равновесия.
Вычисляем Mсеч относительно центра тяжести
растянутой арматуры
Mсеч = Rb b x (h0 – 0,5 x),
(3.4)
или относительно ц. т. бетона сжатой зоны
Mсеч = RS AS (h0 – 0,5 x),
(3.5)
где: h0 – 0,5 x = Zb - плечо внутренней пары сил;
h0 = h – a – рабочая высота сечения;
a – расстояние от центра тяжести растянутой
арматуры до грани сечения
3.3

4.

ξ - относительная высота сжатой зоны бетона
ξ = x / h0,
(3.6)
ξR = xR / h0 = 0,8 / (1 + (εs,eℓ / εb2)), (3.7)
где: xR - граничная высота сжатой зоны;
εs,el - относительная деформация растянутой
арматуры при напряжениях, равных RS,
εs,el = RS / ES ;
εb2 – относительная деформация сжатого
бетона при напряжениях, равных Rb,
принимаемая для тяжелых бетонов класса
В60 и ниже εb2 = 0,0035.
ξ ≤ ξ R.
Рис. 3.3. Схема усилий в нормальном сечении
изгибаемого элемента с одиночной арматурой в
стадии предельного равновесия.
(3.8)
3.4

5.

Найдем площадь поперечного сечения арматуры AS.
Составим систему двух уравнений (3.2) и (3.4) или (3.5), Mult = М.
x = h0 - [h02 - 2М/( Rb b)]0,5,
(3.9)
AS = Rb b h0[1 –(1 –2M/( Rb b h20))0,5]/ RS.
(3.10)
Табличный метод подбора сечений:
A0 = М / (Rb b h20),
ξ = 1 – (1 -2 A0)0,5,
η = 1 – 0,5 ξ,
h0 = (M / (A0 Rb b))0,5 ,
(3.11)
(3.12)
(3.13)
(3.14)
h = h0 + a (округляют до унифицированного размера).
AS = M / (η RS h0).
Mult = A0 Rb b h20.
μs = AS / (b h0) ∙ 100%
(3.15)
(3.16)
(3.17)
μsmin > 0,1 %
μsmax = Rb ∙ ξR ∙ 100% / RS.
μsmax = 1% ÷ 1,5 %.
(3.18)
3.5

6.

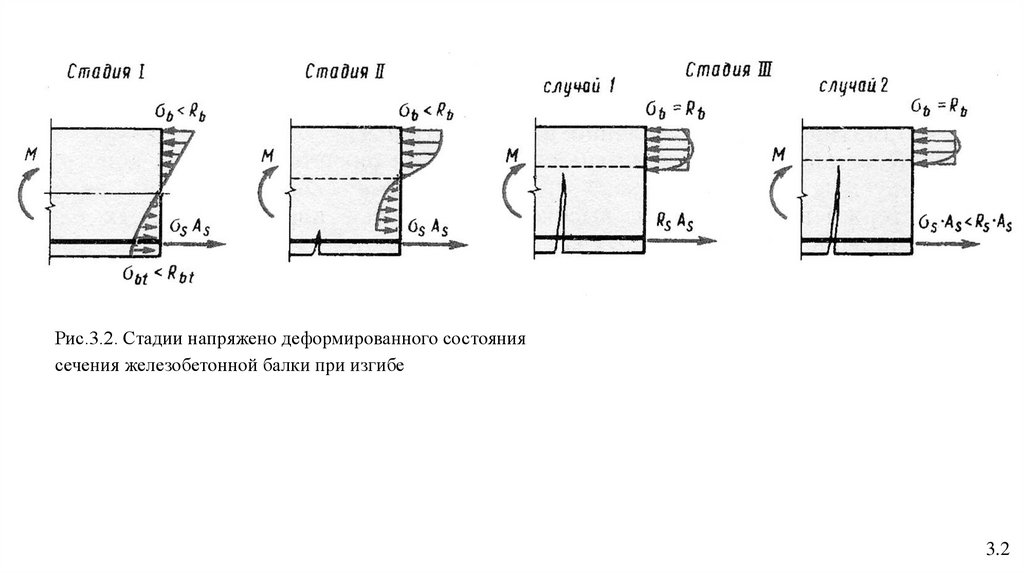
Рис.3.4.1 Схема усилий в сечении
элемента с двойной арматурой.
RS AS - Rb b x - RSC AIS = 0,
(3.19)
где: RSC – расчетное сопротивление арматуры сжатию;
AIS – площадь поперечного сечения сжатой арматуры.
x = (RS AS - RSC AIS)/( Rb b) .
Mult = Rb b x (h0 – 0,5 x) + RSC AIS (h0 – aI),
(3.20)
(3.21)
где: aI - расстояние от центра тяжести сжатой арматуры до
ближайшей грани сечения.
3.6

7.

Рис.3.4. Схема усилий в
сечении элемента с двойной
арматурой:
M ≤ M1 + M2 ,
AS1 = M1 / [RS (h0 – 0,5 x)].
M2 = M – M1,
AIS = M2 / [RSC (h0 – aI)].
AS2 = AIS RSC / RS,
(3.22)
(3.23)
а – схема внутренних усилий;
б – сечение железобетонного
элемента с двойной арматурой;
в – сечение с арматурой в
растянутой зоне;
г – сечение с двойной
арматурой
(3.24)
(3.25)
Определим площадь растянутой арматуры AS
AS = AS1 + AS2.
μsmax = μs - μIS RSC / RS,
(3.26)
(3.27)
где μIS – процент армирования сжатой арматуры;
μIS = AIS RSC / (b h0 RS) ∙ 100%.
(3.28)
3.7

8.

Рис.3.5. Виды железобетонных
конструкций, расчет которых по
прочности сводится к расчету тавра с
полкой в сжатой зоне:
а – тавровая железобетонная балка;
б – двутавровая балка и ее
приведенное тавровое сечение;
в – ребристое монолитное перекрытие;
г – ребристая панель и ее расчетный
эквивалент;
д – панель с круглыми пустотами;
е – панель коробчатого сечении.
3.8

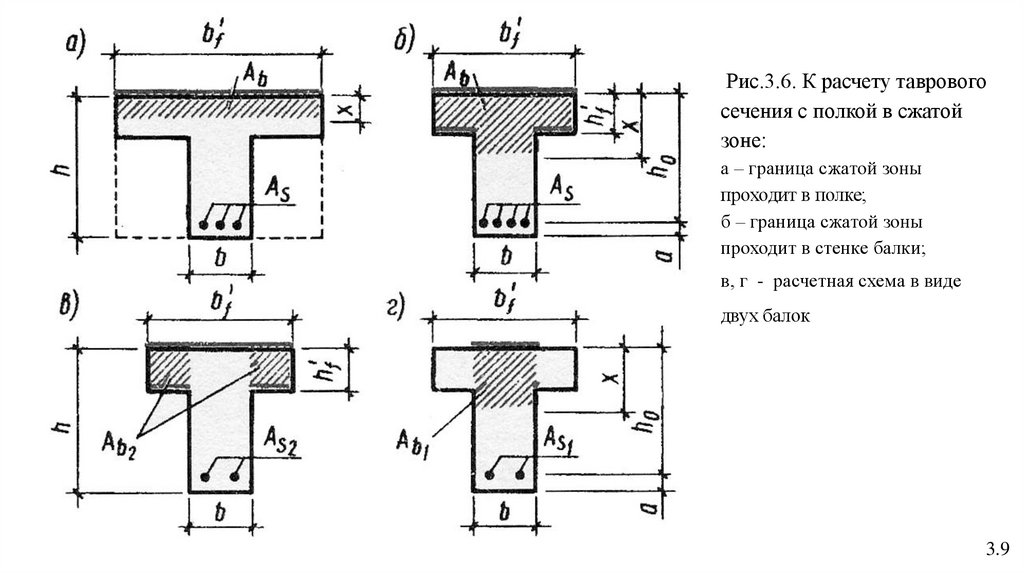
9.

Рис.3.6. К расчету таврового
сечения с полкой в сжатой
зоне:
а – граница сжатой зоны
проходит в полке;
б – граница сжатой зоны
проходит в стенке балки;
в, г - расчетная схема в виде
двух балок
3.9