Подход Лагранжа

1.

Решение задачи 3 (задача 7.3, Векштей)
Условия задачи
• Среда идеальная – нет диссипации энергии
• Частицы пыли не взаимодействуют между собой: «парциальное»
давление пыли отсутствует
• Основания для использования лагранжева подхода
- нужно отслеживать отдельные частицы пыли, что лежит в основе
подхода Лагранжа
- лагранжевы уравнения движения частиц жидкости (пыли) линейны
в отличие от уравнения Эйлера

2.

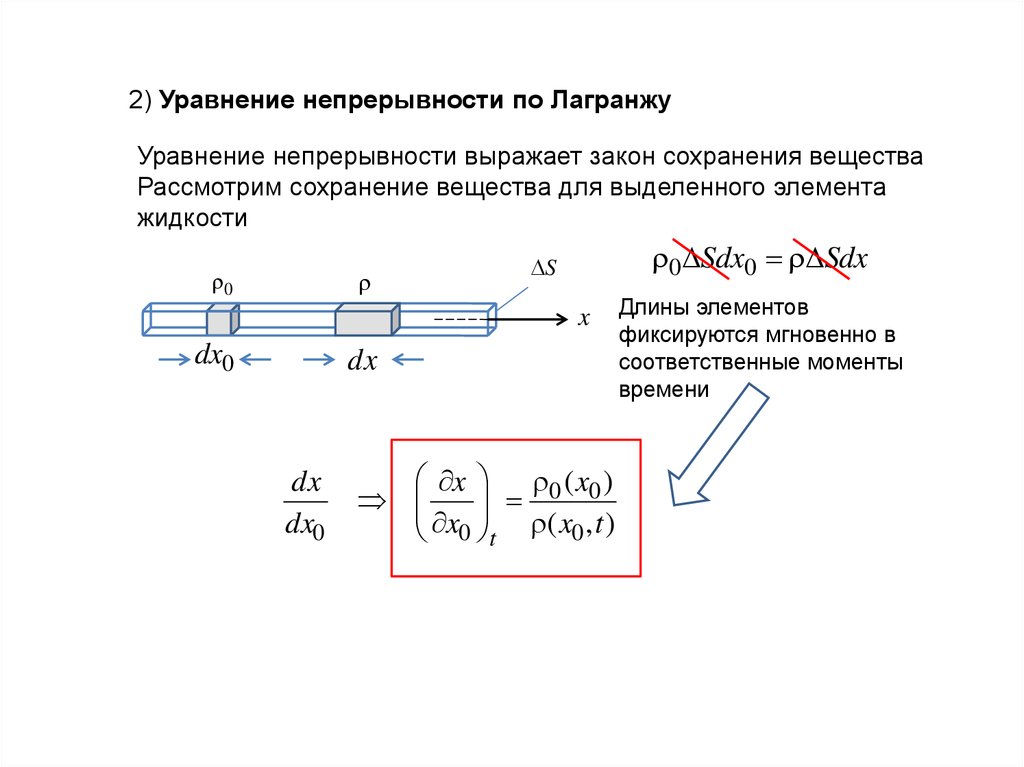
2) Уравнение непрерывности по Лагранжу
Уравнение непрерывности выражает закон сохранения вещества
Рассмотрим сохранение вещества для выделенного элемента
жидкости
0
0 Sdx0 Sdx
S
x
dx0
dx
dx
dx0
x 0 ( x0 )
x0 t ( x0 , t )
Длины элементов
фиксируются мгновенно в
соответственные моменты
времени

3.

3) Уравнение движения по Лагранжу
2x
Выделенный элемент dx испытывает ускорение dm
dm 2
2
t
dt
x0
d 2x
Находится под действием разности сил давления
p
S [ p ( x) p ( x dx)] S dx
x t
p
p( x dx) p( x) dx
x
p(x)
p(x dx)
x
p(x) и p(x dx)
x0
x dx
С учетом действия еще и массовой силы dm f(x, t) по 2-му закону
Ньютона имеем, соотнося элементу значение координаты
2x
p
dx0 S dmf ( x0 , t )
dm 2
t
x0 t
x0
Так как dm Sdx ,
получаем

4.

2x
p dx0 S f ( x0 , t )
x Sdx
t 2
0 t
x0
Из закона сохранения вещества dx 0dx0
Поэтому
2 x
p 1 f ( x0 , t )
x
t 2
0 t 0
x0
p
0 f ( x0 , t ) 0
4) Решение задачи По условиям задачи
x0 t
2
Уравнение движения x
x x0 v( x0 )t
0
дает
t 2
x0
Величину начального распределения скорости v( x0 ) Найдем из
x
заданного поля скоростей v( x) v0 sin заменой x x0
l

5.

x
v( x0 ) v0 sin 0 Отсюда имеем связь лагранжевой координаты x
l c ее начальным значением x0
x
x x0 v0t sin 0
l
(1)
Цель решения – нахождение распределения плотности частиц ( x0 , t )
Эта величина входит в закон сохранения вещества:
x 0 ( x0 )
x0 t ( x0 , t )
( x0 , t )
0 ( x0 )
x
x0 t
(2)
Из (1) дифференциированием
получаем
x
x
1 v0t cos 0
l
l
x0 t
( x0 , t )
0 ( x0 )
x
1 v0t cos 0
l
l

6.

Обозначая исходное распределение плотности 0 ( x0 ) 0
имеем окончательно
( x0 , t )
0
x
1 v0t cos 0
l
l
5) Обсуждение и выводы
• Вместо ( x0 , t ) можно рассмотреть используя (1) ( x, t )
Однако в этом случае вследствие зависимости x от t не
удается установить распределения плотности в фиксированные
моменты времени
• Формула показывает изменения распределения плотности частиц
по координате начальных положений со временем, в частности
предсказывает возникновение сингулярных особенностей при
1
x
v0t cos 0 0
l
l

7.

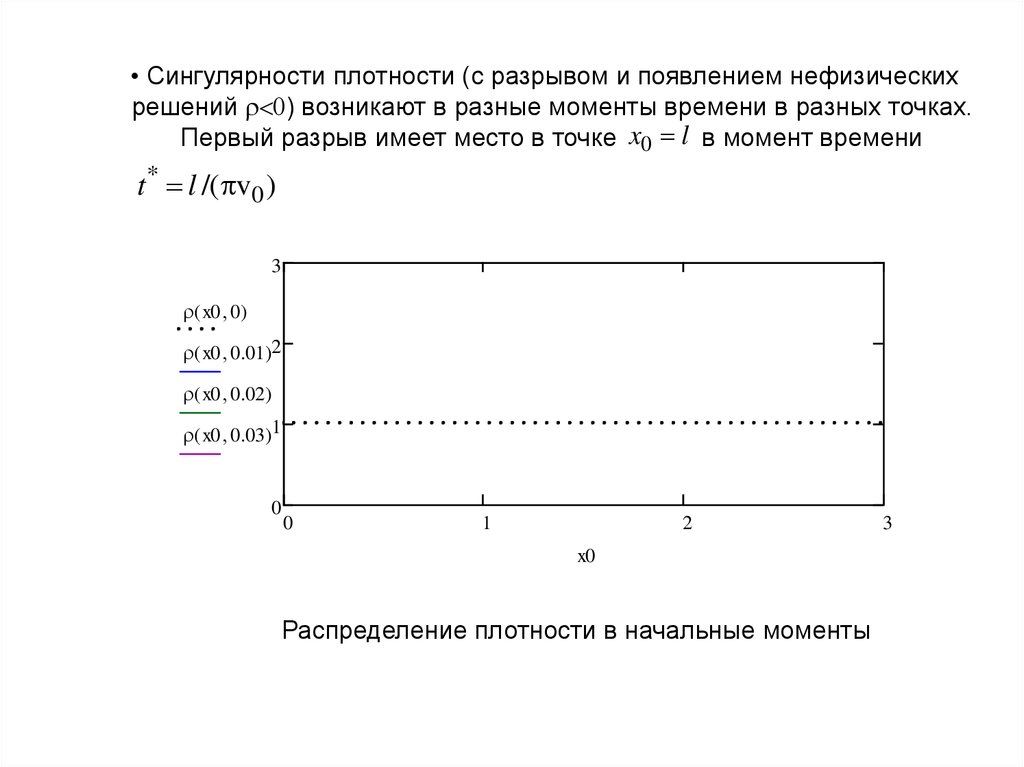
• Сингулярности плотности (с разрывом и появлением нефизических
решений ) возникают в разные моменты времени в разных точках.
Первый разрыв имеет место в точке x0 l в момент времени
t* l /( v0 )
3
( x0 0)
( x0 0.01)2
( x0 0.02)
( x0 0.03)1
0
0
1
2
x0
Распределение плотности в начальные моменты
3

8.

4
1 10
3
( x0 0)
1 10
( x0 0.04)
100
( x0 0.0476)
( x0 0.20)
10
1
0.1
0
0.5
1
1.5
x0
7
1 10
5
( x0 0)
1 10
( x0 0.04775)
1 10
( x0 20.0)
3
10
0.1
3
1 10
0
0.5
1
1.5
x0
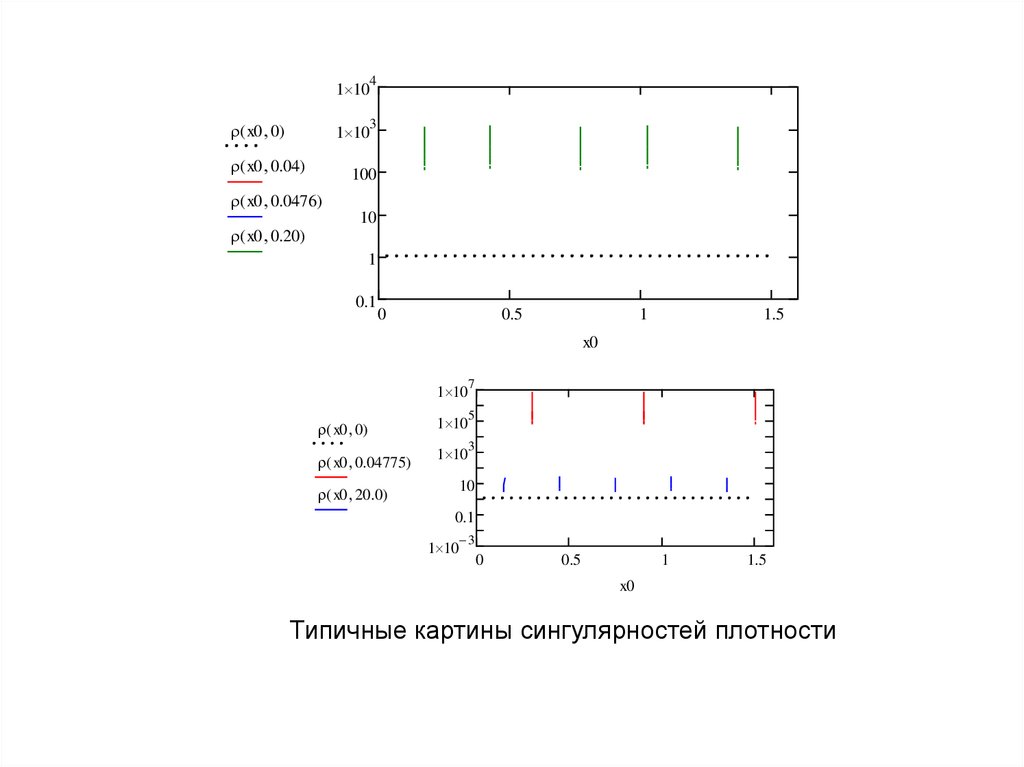
Типичные картины сингулярностей плотности

9.

1
x( t 1)
x( t 0.5)
0.5
x( t 0.0)
x( t 0.5)
0
x( t 1) 0.5
1
0
0.2
0.4
0.6
t
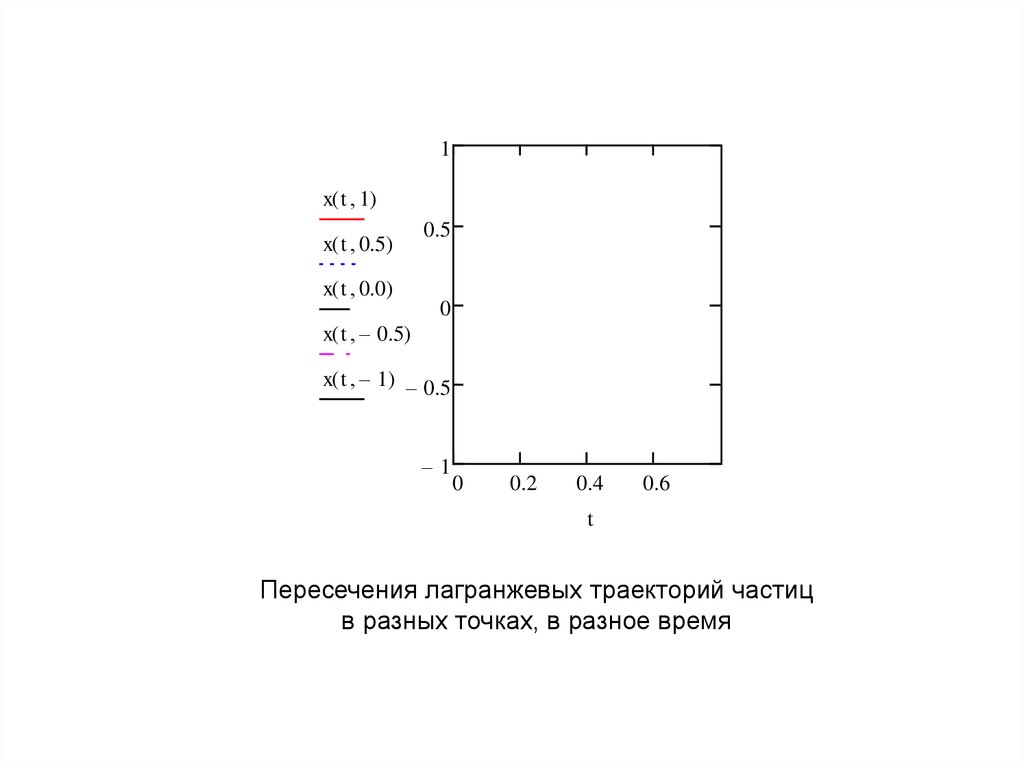
Пересечения лагранжевых траекторий частиц
в разных точках, в разное время

10.

X0( 30 t )
X0( 20 t )
0.1
X0( 5 t )
X0( 0.5 t )0.05
0
0
20
40
60
80
100
t
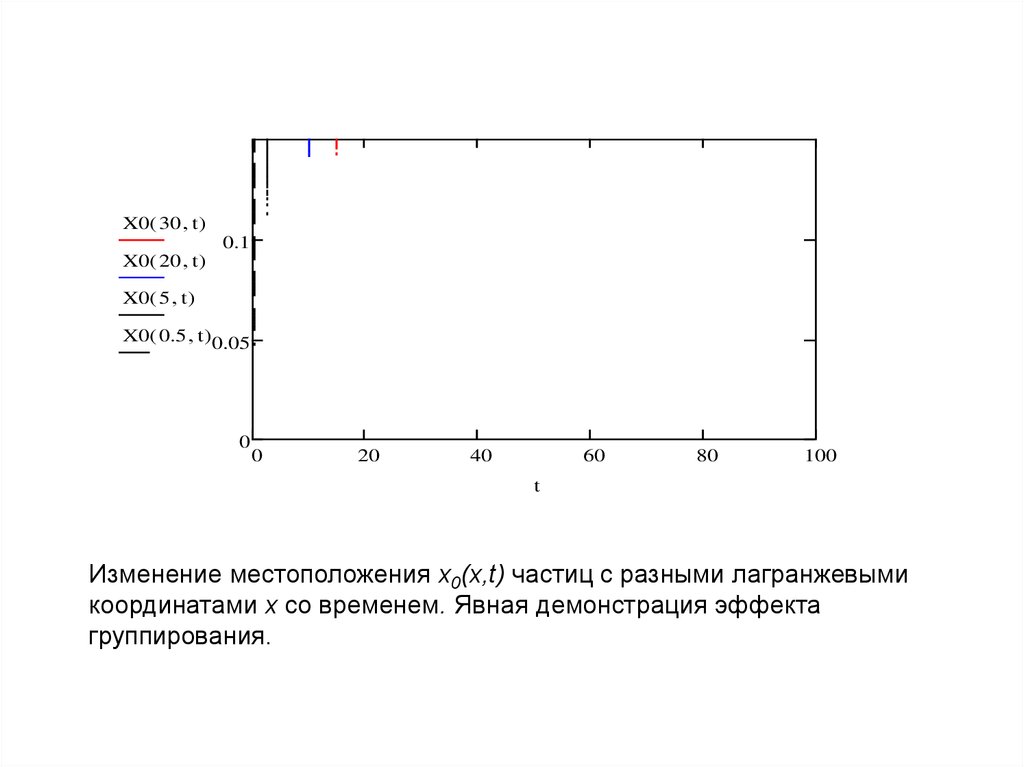
Изменение местоположения x0(x,t) частиц с разными лагранжевыми
координатами x со временем. Явная демонстрация эффекта
группирования.

11.

0.03
X0( 30 t )
0.02
X0( 20 t )
X0( 5 t ) 0.01
0
0
3
1 10
3
2 10
t
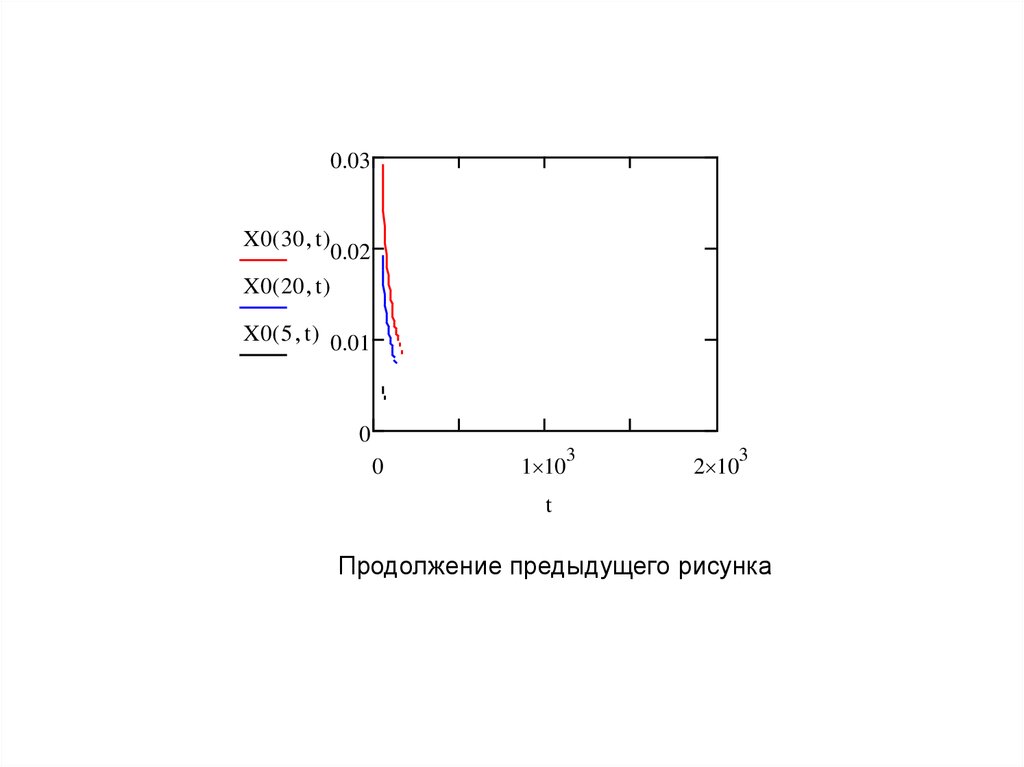
Продолжение предыдущего рисунка

12.

Основной вывод: жидкость (газ) представляют собой
существенно нелинейную систему; сингулярности – следствие
идеализации (необходим учет вязкости и диссипации энергии)