Практика. «Булевы функции от двух переменных». Определение

1.

Практика. «Булевы функции от
двух переменных»
Определение

2.

Определение
• Определение: Булевой функцией от двух
аргументов называется функция g,
заданная на множестве {0,1}х{0,1} и
принимающая значения в двух элементном
множестве {0,1}.
• Область определения функции состоит из
четырех упорядоченных пар составленных
из 0 и 1.

3.

Примеры булевых функций:
• примеры элементарных булевых функций:
• ¬х; х&у; хVу; х→у;х↔у. Определение их
было дано раньше.
• g(х)=0- константа 0 (тождественный ноль);
• g(х)=1-константа 1(тождественная
единица);
• g(х)=х-тождественная функция.

4.

Штрих Шеффера- отрицание
конъюнкции
• Обозначение хȁ у
• хȁ у отрицание конъюнкции.
• Принимает значение 0 в том и только том
случае, когда аргументы оба принимают
значения 1.
• Например:g(1,1)=1ȁ 1 =0; g(1,0)= 1ȁ 0 =1

5.

Упражнение
• Выразить через штрих Шеффера функции:
• В правильности первых четырех убедиться, пятую и шестую
получить самостоятельно.
• 1)¬х=х ȁх
• Составим таблицу истинности функции стоящей справа и
функции слева
• 2)х&у=(х|у)|(х|у)
• Составим таблицу истинности функции стоящей справа и
функции слева
• 3)хVу = ( х|х)|(у|у)
• Составим таблицу истинности функции стоящей справа и
функции слева
• 4)х→у=? 5)х↔у=?

6.

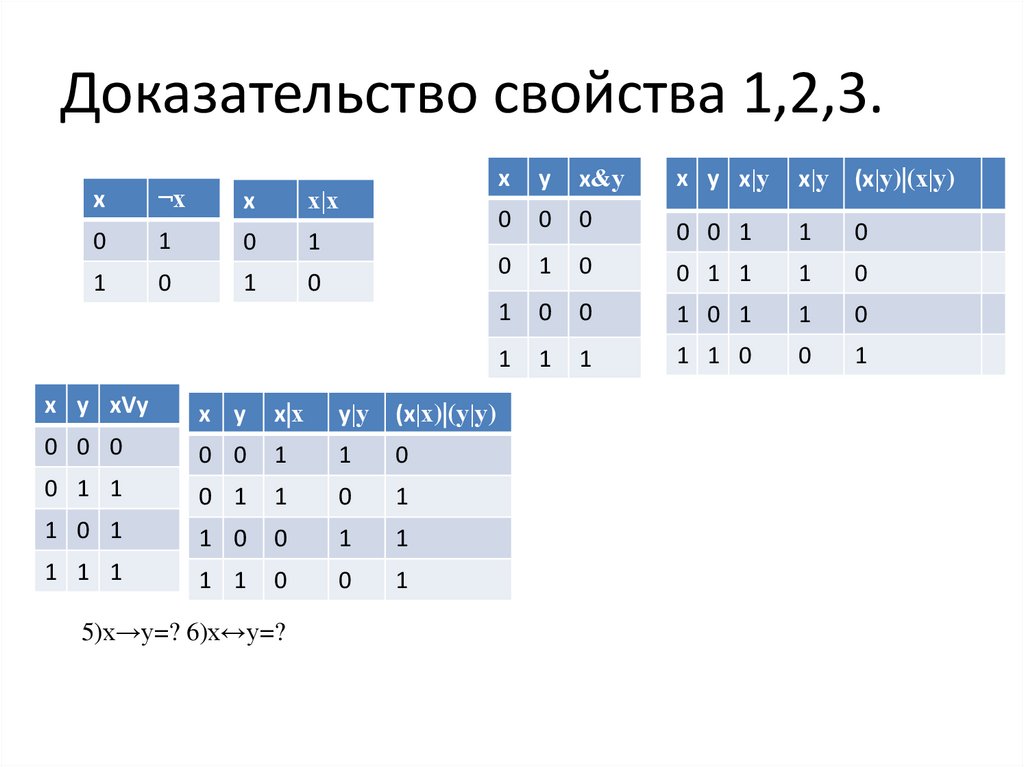
Доказательство свойства 1,2,3.
х
¬х
х
х|х
0
1
0
1
1
0
1
0
х у хVу
х у
х|х
у|у
(х|х)|(у|у)
0 0 0
0 0
1
1
0
0 1 1
0 1
1
0
1
1 0 1
1 0
0
1
1
1 1 1
1 1
0
0
1
5)х→у=? 6)х↔у=?
х
у
х&у
х у х|у
х|у (х|у)|(х|у)
0
0
0
0 0 1
1
0
0
1
0
0 1 1
1
0
1
0
0
1 0 1
1
0
1
1
1
1 1 0
0
1

7.

• Ответ:5)х→у=х|(у|у) 6) Самостоятельно.
• 5.Просчитать по образцу.(см.предыдущий
слайд)
• 6.а) Использовать теорему 3.( смотри лекции
С.С. Коробкова) эвиваленцию представить
через импликацию)
• б) использовать св- во 5.
• Решение отправить мне на проверку 5 и6
• Это задание 1

8.

Полная система функций.
• Определение: Система функций {f, g,…q,…}
называется полной, если любая булева
функция может быть записана в виде
формулы через функции этой системы.
• Выполненное упражнение позволяет
сделать вывод, что система {|} полная.

9.

Стрелка Пирса (функция Веббера)
• Обозначение g(х,у)=х ↓у
• Определение: Функция стрелка Пирса
является отрицанием дизъюнкции то есть
принимает значение 1 в одном и только
одном случае когда оба аргумента нули.

10.

Упражнения
• Выразить через стрелку Пирса следующие функции:
• В правильности первых трех убедиться составляя
таблицы истинности правой и левой функции.
• 1)¬х=х↓ х
• 2)х&у=(х↓ х)↓ (у↓ у)
• 3)хVу=(х↓ у) ↓(х↓ у)
• 4 и 5 функции представить самостоятельно
• 4)х→у=?
• 5)х↔у=?

11.

• Ответ: 4)х→ у= ((х ↓х) ↓у)↓(( х↓ х)
5)х↔у=? Д.З За образец выполнения взять
указания к пункту 6 (штрих Шеффера).
Задание 2 Решение пункта 4.

12.

• Выполненное упражнение позволяет
сделать вывод что система {↓} полная.

13.

Сумма Жегалкина (сложение по
модулю два)
• Обозначение суммы Жегалкина х+у
• Определение: Функция сумма Жегалкина
• принимает значение 0 тогда и только тогда
когда оба аргумента принимают
одинаковые значения.
• Примеры:g(1,0)=1+0=1; 1+1=0

14.

Упражнения
• Выразить через сумму Жегалкина
следующие функции:
• 1)¬х=х+1;
• 2)х↔у=х+у+1
• 3)х|у=х+у+1
• Задание 3 Выполнить по образцу задания
1. (см.упр.о штрих Шеффера)

15.

Примеры полных систем.
• А) Система Р2 множество всех булевых
функций;
• Б) Система {¬х, х&у, хVу};
• D) Система {¬х, хVу};
• C) Система {0, 1, х&у, х+у }.

16.

Задание 4
• Доказать что система {0, 1, х&у, х+у }
полная
• Задание 5 Обладает ли свойством
ассоциативности, коммутативности
а)импликация?
• б)стрелка Пирса?

17.

Полиномы Жегалкина
• Полиномом Жегалкина степени не выше
первой называется булева функция
f(х1, х2….. х