Similar presentations:
Элементарные булевы функции одной и двух переменных
1.
Джордж Буль(2 ноября 1815 - 8 декабря 1864 г.)
2.
xf1
f2
f3
f4
0
0
0
1
1
1
0
1
0
1
3.
,Тождественным нулем называется булева
функция одной переменной, если она принимает
значение, равное нулю, при любом значении
переменной
f (x)=0
1
4.
,Тождественной единицей называется булева
функция одной переменной, если она принимает
значение, равное единице, при любом значении
переменной
f (x)=1
4
5.
,Тождественной называется булева функция
одной переменной , если она принимает значение,
совпадающее со своим аргументом
f2(x)=x
6.
Отрицанием (инверсией) называется булевафункция одной переменной, если она принимает
значение, противоположное своему аргументу
f (x)= x
3
7.
xy
f1
f2
f3
f4
f5
f6
f7
f8
f9
f10
f11
f12
f13
f14
f15
f16
0
0
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
0
1
0
0
0
0
1
1
1
1
0
0
0
0
1
1
1
1
1
0
0
0
1
1
0
0
1
1
0
0
1
1
0
0
1
1
1
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
8.
Конъюнкцией называется булева функция двухпеременных, если она принимает значение, равное
единице, в том и только том случае, если обе ее
переменные обращаются в единицу
f2(x,y) х у
9.
Дизъюнкцией называется булева функция двухпеременных, если она принимает значение, равное
нулю, в том и только том случае, если обе ее
переменные обращаются в нуль
f8(x,y) х у
10.
Импликацией из x в y называется булевафункция двух переменных, если она принимает
значение, равное нулю, в том и только том случае,
если переменная x принимает значение, равное
единице, а переменная y – равное нулю
f14(x,y) х у
11.
Эквиваленцией называется булева функция двухпеременных , если она принимает значение, равное
единице, в том и только том случае, если значения ее
переменных совпадают
f10(x,y) х у
12.
Суммой по модулю два называется булевафункция двух переменных, если она принимает значение,
равное единице, в том и только том случае, если значения
ее переменных не совпадают
f7(x,y) х у
13.
Штрихом Шеффера называется булева функциядвух переменных, если она принимает значение, равное
нулю, в том и только том случае, если обе ее переменные
обращаются в единицу
f15(x,y) х у
14.
Стрелкой Пирса называется булева функциядвух переменных, если она принимает значение,
равное единице, в том и только том случае, если
обе ее переменные обращаются в нуль
f9(x,y) х у
15.
При построении таблицы значений булевой функции, заданнойаналитически, будем использовать следующий алгоритм:
найти количество строк таблицы значений по формуле ,
где n – число переменных функции; при этом нужно
иметь в виду, что строка – заголовок в это число не
входит
заполнить первые столбцы таблицы значений,
отвечающие за переменные функции, по принципу
половинного деления
16.
найти количество столбцов таблицы значений, котороеравно сумме числа переменных функции и булевых
функций, определяющих данную функцию
композиционно, и заполнить оставшиеся ячейки строки –
заголовка в соответствии с приоритетом булевых функций
заполнить остальные столбцы таблицы в соответствии с
определениями или таблицами значений элементарных
булевых функций одной и двух переменных, учитывая, что
при заполнении каждого столбца соответствующее
определение применяется к значениями одного или двух
столбцов, расположенных левее заполняемого
17.
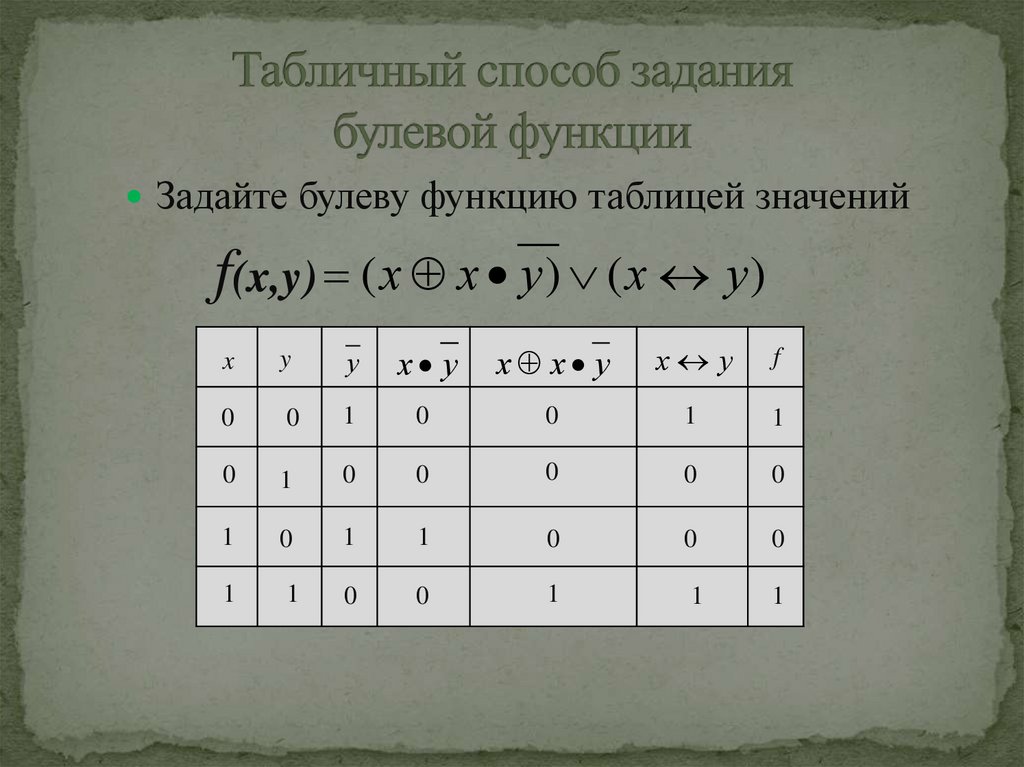
Задайте булеву функцию таблицей значенийf(x,y) ( х х у ) ( х у )
x
y
у
х у
х х у
х у
f
0
0
1
0
0
1
1
0
1
0
0
0
0
0
1
0
1
1
0
0
0
1
1
0
0
1
1
1
18.
Задайте геометрически булеву функциюf(x,y)= (( x y) y) xy
x
y
x y
y
0
0
0
1
1
0
0
1
0
1
1
0
1
0
0
1
1
0
1
1
0
0
1
0
1
1
1
0
1
1
1
0
( x y ) y ) xy (( x y) y) xy f
19.
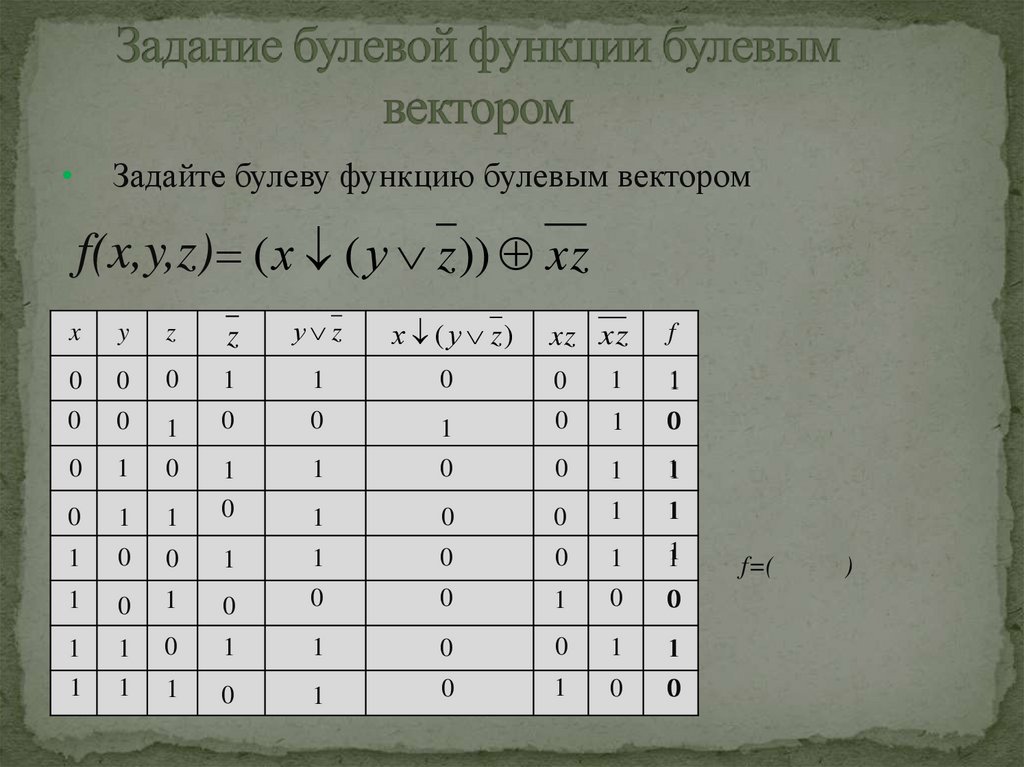
Задайте булеву функцию булевым вектором
f(x,y,z) ( х ( у z )) xz
x
y
z
z
у z
х ( у z)
0
0
0
1
1
0
0
0
1
0
0
0
1
0
1
0
1
1
1
0
1
xz xz
f
0
1
1
1
0
1
0
1
0
0
1
1
0
1
0
0
1
1
0
1
1
0
0
1
11
0
1
0
0
0
1
0
0
1
1
0
1
1
0
0
1
1
1
1
1
0
1
0
1
0
0
f=(
)
20.
.Две булевы функции n переменных называются
равными, если они принимают одинаковые
значения при любых соответствующих значениях
их аргументов
f g
21.
Проверьте равенство булевых функцийf ( x, y , z ) x ( у z )
g ( x, y, z ) xy xz
x
y
z
у z
f
xy
xz
g
0
0
0
0
0
0
0
0
0
0
1
1
0
0
0
0
0
1
0
1
0
0
0
0
0
1
1
1
0
0
0
0
1
0
0
0
0
0
0
0
1
0
1
1
1
0
1
1
1
1
0
1
1
1
0
1
1
1
1
1
1
1
1
1
x( у z ) xy xz
f=g
22.
x( у z ) xy xzТаким
образом,
для
булевых
функций
справедливы свойства, аналогичные законам
алгебры логики. Техника их использования ничем
не отличается от техники равносильных
преобразований формул алгебры логики




















 mathematics
mathematics