Экстремум функции двух переменных

1.

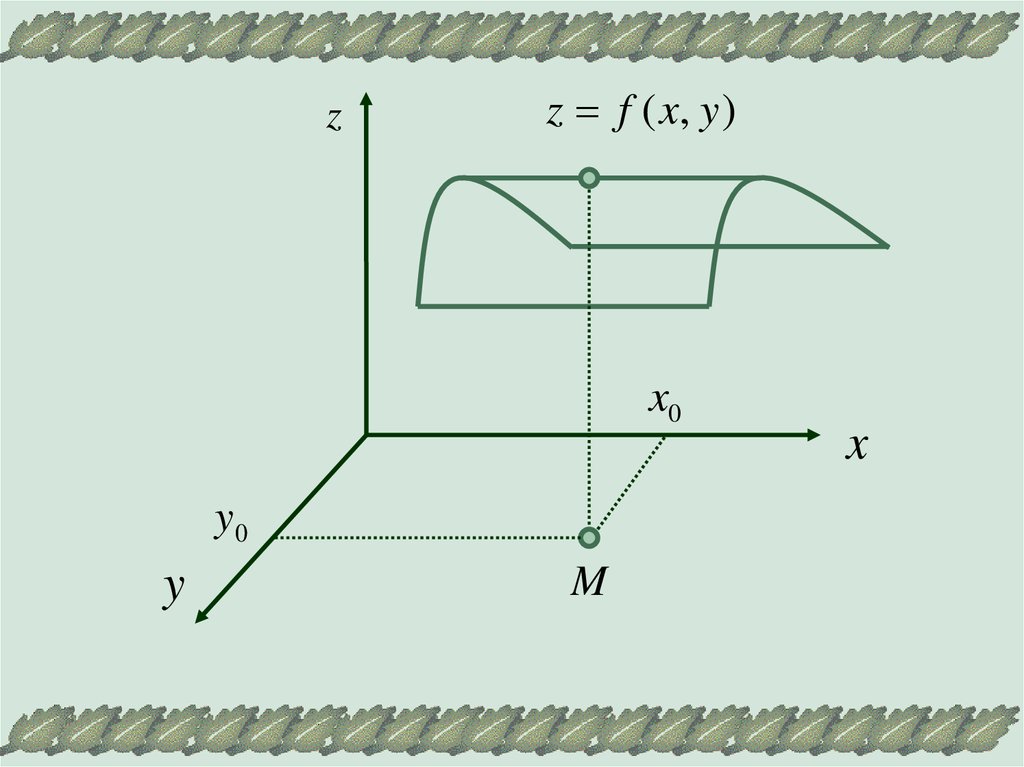
Как и в случае функции одной переменной, функция
z=f(x,y) имеет узловые, определяющие график
функции, точки.
Определим точки экстремума для функции двух
переменных.

2.

Точка М(х0,у0) называется точкой
максимума (минимума) функции z=f(x,y),
если существует окрестность точки М,
такая что для всех точек (х,у) из этой
окрестности выполняется неравенство:
f ( x0 , y0 ) f ( x, y)
f ( x0 , y0 ) f ( x, y)

3.

Экстремум имеет локальный характер, поскольку
рассматривается максимальное и минимальное
значение
функции
в
достаточно
малой
окрестности точки М(х0,у0).
Сформулируем аналог теоремы Ферма для
функции двух переменных:

4.

Пусть точка (х0,у0) является точкой
экстремума дифференцируемой функции
z=f(x,y).
Тогда частные производные в этой точке
f x ( x0 , y0 )
равны нулю:
f y ( x0 , y0 )
f x ( x0 , y0 ) 0
f y ( x0 , y0 ) 0

5.

Пусть точка М(х0,у0) – точка максимума.
Зафиксируем одну из переменных, например, у:
у=у0
Тогда получим функцию одной переменной
z1=f(х,у0)
которая будет иметь максимум при х=х0.
Согласно теореме Ферма z1 ( x0 ) f x ( x, y0 ) 0
Аналогично можно доказать, что
f y ( x0 , y ) 0

6.

Точки, в которых выполняются условия
экстремума функции z=f(x,y), т.е.
z x 0
z y 0
называются критическими или
стационарными.

7.

Необходимое
условие
сформулировать иначе:
экстремума
можно
В точках максимума или минимума
дифференцируемой функции градиент этой
функции равен нулю:
z 0

8.

z
z f ( x, y )
x
y

9.

Однако, сформулированное выше условие является
необходимым, но не достаточным.
Т.е., если частные производные функции в точке
равны нулю, то это еще не означает, что в данной
точке имеется экстремум функции.
Например:

10.

z
z f ( x, y )
x0
y0
y
M
x

11.

В точке М(х0,у0) выполняется необходимое условие
экстремума:
f x ( x0 , y0 ) 0
f y ( x0 , y0 ) 0
Но эта точка не является точкой экстремума.
Она называется седловой точкой (аналог точки
перегиба).
Чтобы отличать такие точки от точек экстремума,
необходимо рассмотреть достаточное условие
экстремума.

12.

Пусть функция z=f(x,y)
1
Определена в некоторой окрестности
критической точки (х0,у0), в которой
f x ( x0 , y0 ) 0
f y ( x0 , y0 ) 0

13.

2
Имеет в этой точке непрерывные
частные
производные
второго
порядка:
( xy) A
f xx
f xy ( xy) f yx ( xy) B
( xy) C
f yy

14.

Тогда, если A C B 2 0
то в данной точке функция имеет
экстремум, причем
если А>0, то минимум
если А<0, то максимум
если A C B 2 0
то функция экстремума не имеет,
если A C B 2 0
то вопрос остается открытым.

15.

1
Найти частные производные
z x f x ( x, y )
z y f y ( x, y )

16.

2
Решить систему уравнений
z x 0
z y 0
и найти критические точки

17.

3
Найти частные производные
второго порядка, вычислить
их значения в критических точках
и с помощью достаточного условия
экстремума сделать вывод о
наличии экстремума функции.

18.

4
Найти значения функции в точках
экстремума.

19.

Найти экстремум функции
z x y 3xy
3
3

20.

z
2
zx
3x 3 y
x
3x 2 3 y 0
2
3 y 3x 0
z
2
zy
3 y 3x
y
x1 0 x2 1
y1 0 y2 1

21.

z
6 y
2
y
2
z
6x
2
x
2
2 z
2 z
3
x y y x
A1 0
B1 0
C1 3
9
Экстремума нет.

22.

A2 6
B2 6
C1 3
27
Экстремум есть.
Т.к. А<0, то это будет максимум.