Similar presentations:
Логарифмы и неравенства
1. Логарифмы
log a b n a bn
n log a a
a
b
n
log a b n log a b при нечётном n
n
log a b n log a b при чётном n
n
1
log a n b log a b
n
1
log a n b log a b
n
loga b
при нечётном n
при чётном n
2.
log a b log a c log a (bc)log a n
k
a
n
k
b
log a b log a c log a
c
1
log a b
log b a
log a b log b a 1
log c b
log a b
log c a
a
logc b
b
log a b log b с log a c
logc a
3.
НЕРАВЕНСТВАНеравенства умножать на
знаменатель нельзя!
Исключение: знаменатель имеет
постоянный знак (не равный нулю)
при любых значениях переменной.
4.
1. Рациональные.1) Прежде чем приводить к общему знаменателю, проверь,
не сокращаются ли отдельные дроби. Если да, то
сократи, взяв на заметку соответствующее ограничение.
1)
Приведи к каноническому виду:
( x a1 ) ... ( x an )
0
( x b1 ) ... ( x bk )
а) При этом помни, что однократное умножение/деление на
отрицательное число меняет знак неравенства,
2
ax
bx c a( x x1 )( x x2 ) Особенно не теряй а.
б)
в) если множитель в виде квадратного трёхчлена имеет
D < 0, то он имеет постоянный знак - такой же как его
старший коэффициент, и на этот множитель неравенство
можно умножить / разделить с соответствующим
отношением к знаку неравенства.
3) Помни о чётных кратностях, если они есть
4) Внимательно запиши ответ: не забудь об отдельных
закрашенных точках и взятых на заметку ограничениях.
5.
Рационализация - замена нерационального множителярациональным.
Замене подвергается только множитель /
делитель в составе произведения / частного,
сравниваемого с нулём!
log a b (a 1)(b 1)
log a b log a c (a 1)(b c)
log a c log b c (a 1)(b 1)(c 1)(b a)
a a (a 1)(b c)
b
c
a b (a b)c
c
c
a b a b
a b a b
a b (a b)(a b)
2
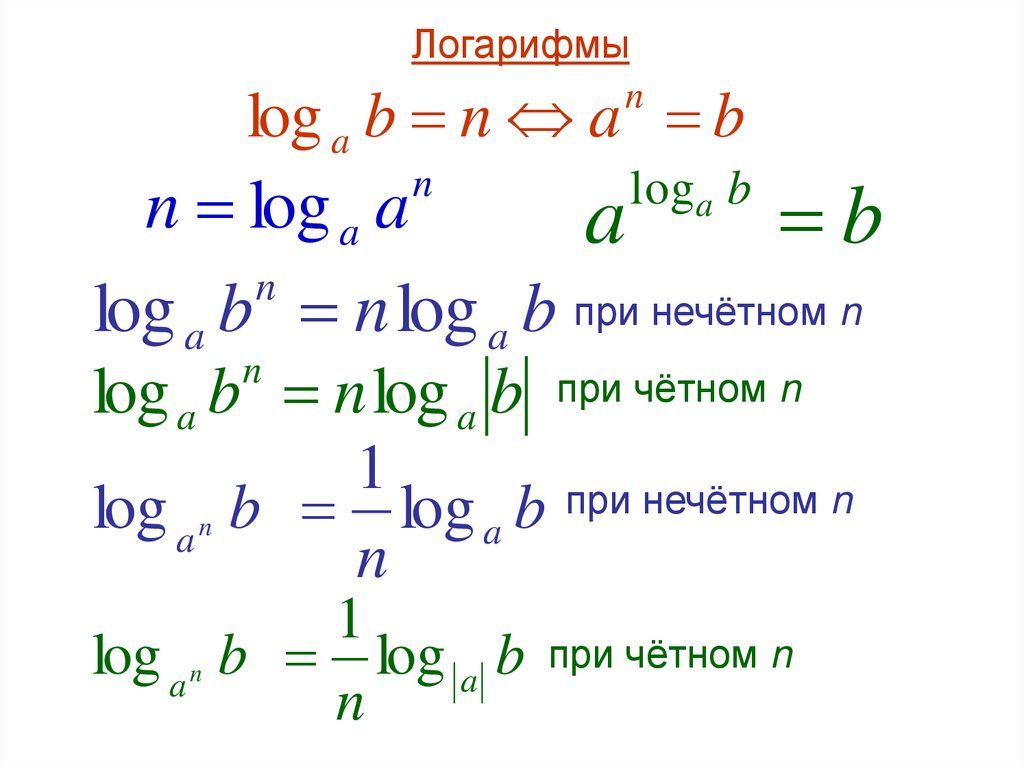
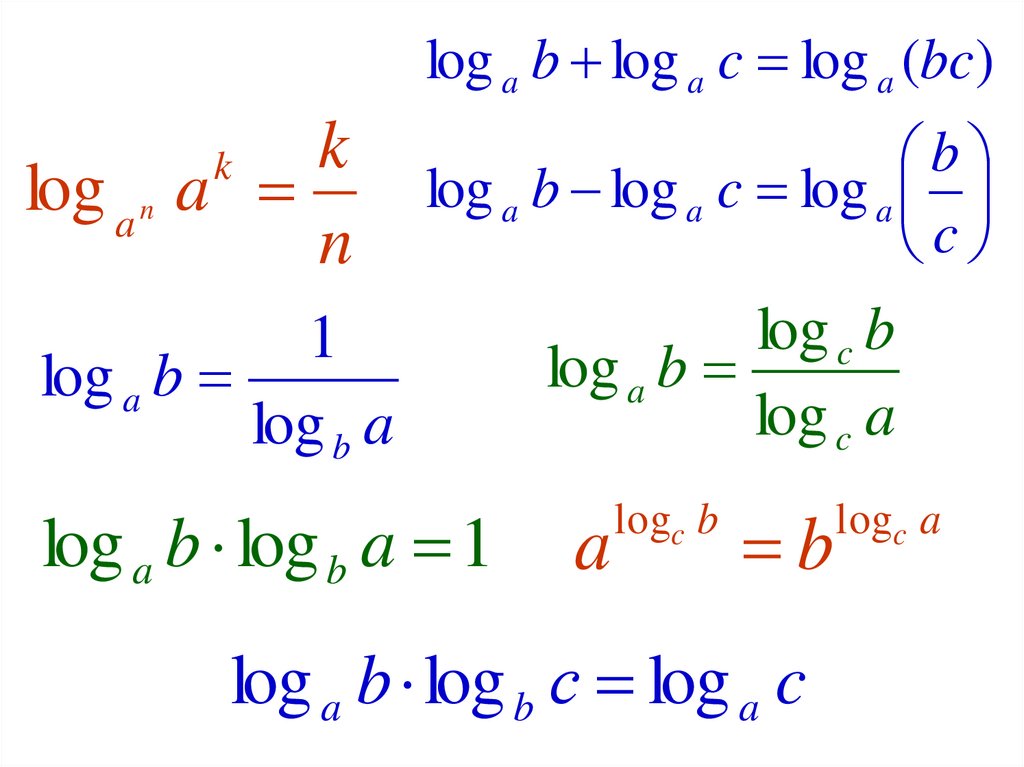



 mathematics
mathematics








