Similar presentations:
Статически определимые и статически неопределимые стержневые системы, работающие на растяжение и сжатие
1.
Статически определимые истатически неопределимые
стержневые системы, работающие
на растяжение и сжатие
1/8
2.
Сведения из предыдущей темыЗакон Гука
Fl0
l
EA0
pr ; (3 ) (1 )
(1`)
(2`)
E
2
3.
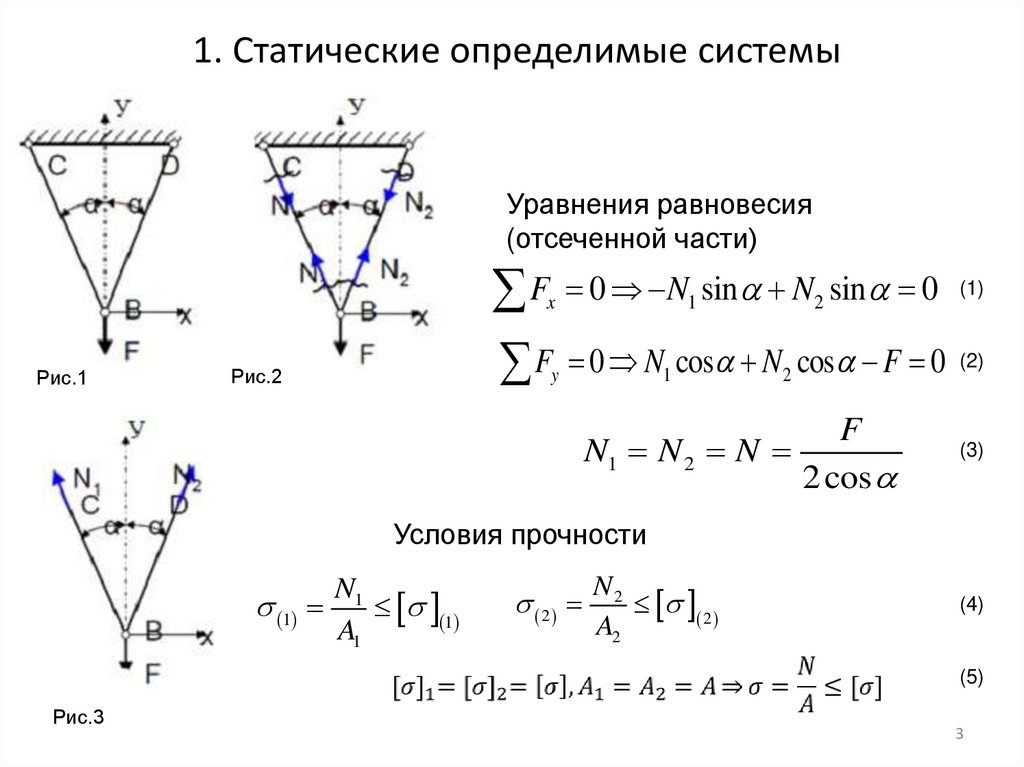
1. Статические определимые системыУравнения равновесия
(отсеченной части)
F 0 N sin N sin 0
F 0 N cos N cos F 0
x
Рис.1
Рис.2
1
y
1
2
2
F
N1 N 2 N
2 cos
(1)
(2)
(3)
Условия прочности
N
1 1 1
A1
2
N2
2
A2
(4)
(5)
Рис.3
3
4.
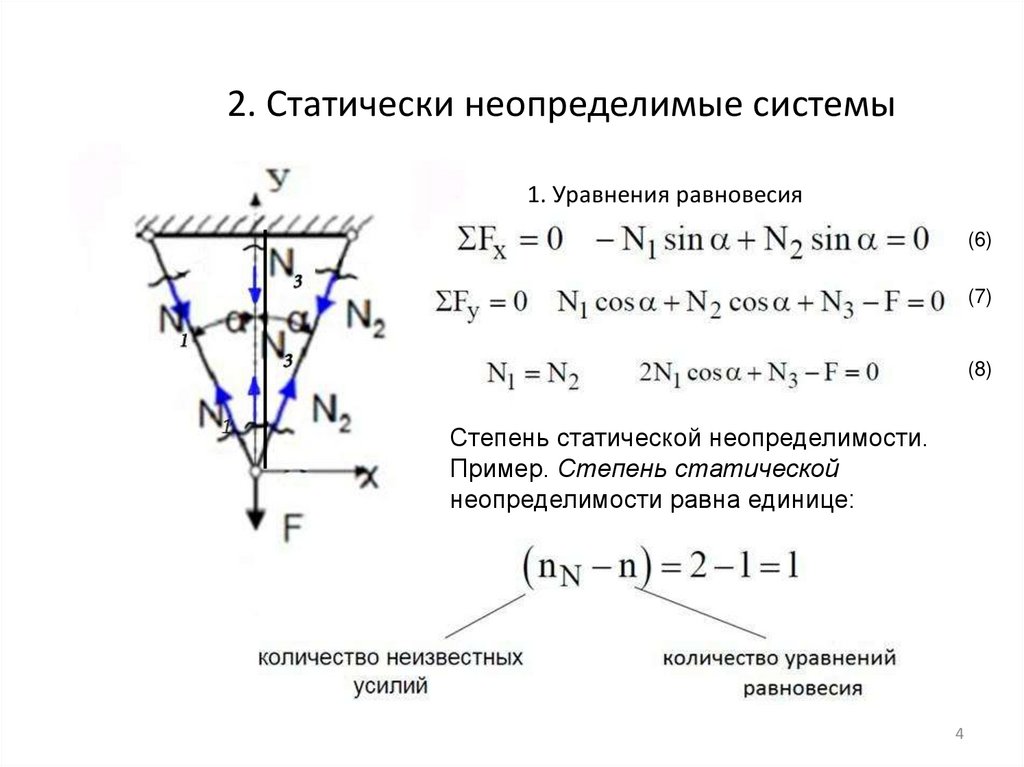
2. Статически неопределимые системы1. Уравнения равновесия
(6)
(7)
(8)
Степень статической неопределимости.
Пример. Степень статической
неопределимости равна единице:
4
5.
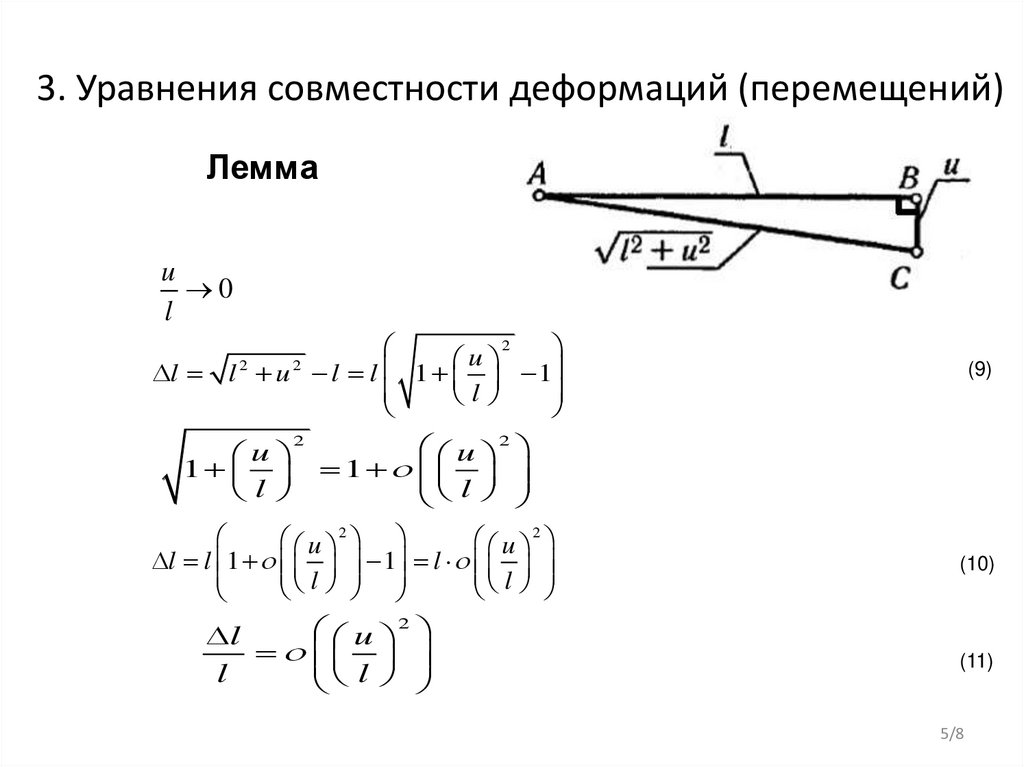
3. Уравнения совместности деформаций (перемещений)Лемма
u
0
l
l
2
u
2
2
l u l l 1 1
l
u
1
l
2
(9)
u 2
1
l
u 2
u 2
l l 1 1 l
l
l
u 2
l
l
l
(10)
(11)
5/8
6.
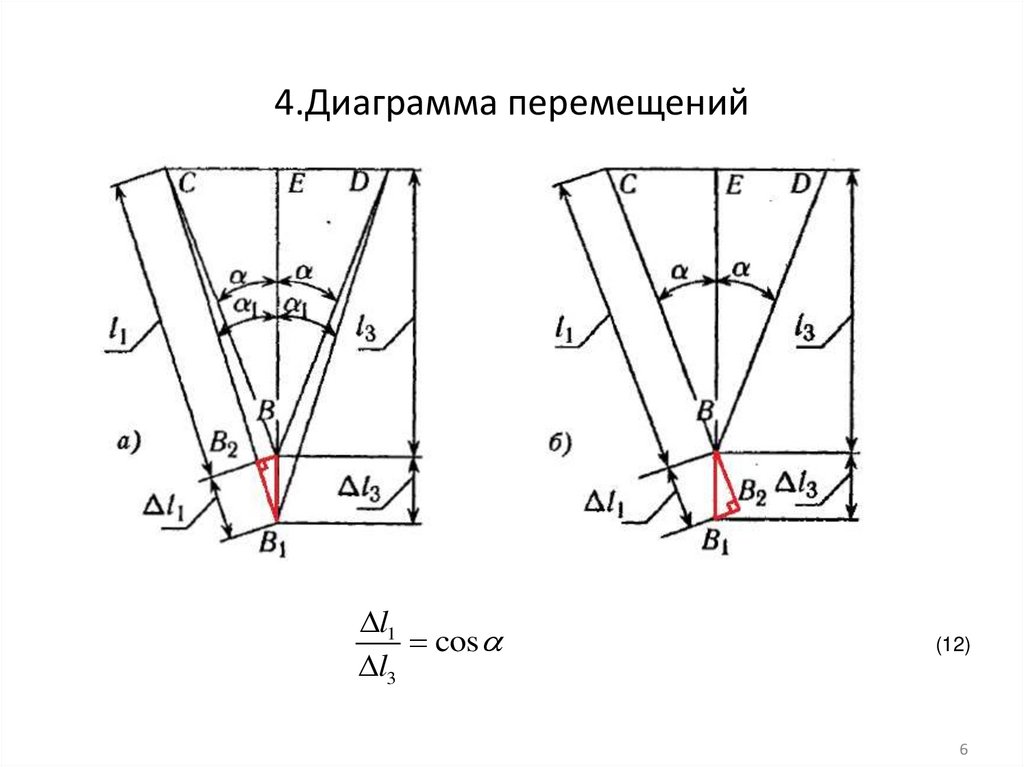
4.Диаграмма перемещенийl1
cos
l3
(12)
6
7.
5.Система уравнений для решения задачи1. Уравнения равновесия
2 N1 cos N3 F 0
2.Уравнения совместности деформаций
(перемещений)
l1
cos
l3
(8’)
(12’)
3.Определяющие уравнения (уравнения состояния)
N1l1
l1
E1 A1
Nl
l3 3 3
E3 A3
(13)
(14)
7
8.
l3 E1 A1cos
(13),(14) -> (12’) => N1 N 3
l1 E3 A3
->(8’)=>
N3
(15)
F
l3 E1 A1
2
2
cos 1
l1 E3 A3
l3 E1 A1
N1
cos
(16) -> (15)=>
l3 E1 A1
2
cos 2 1 l1 E3 A3
l1 E3 A3
F
Условие прочности
(1)
N1
... (1)
A1
N3
(3)
... (3)
A3
(16)
(17)
(18)
(19)
8
9.
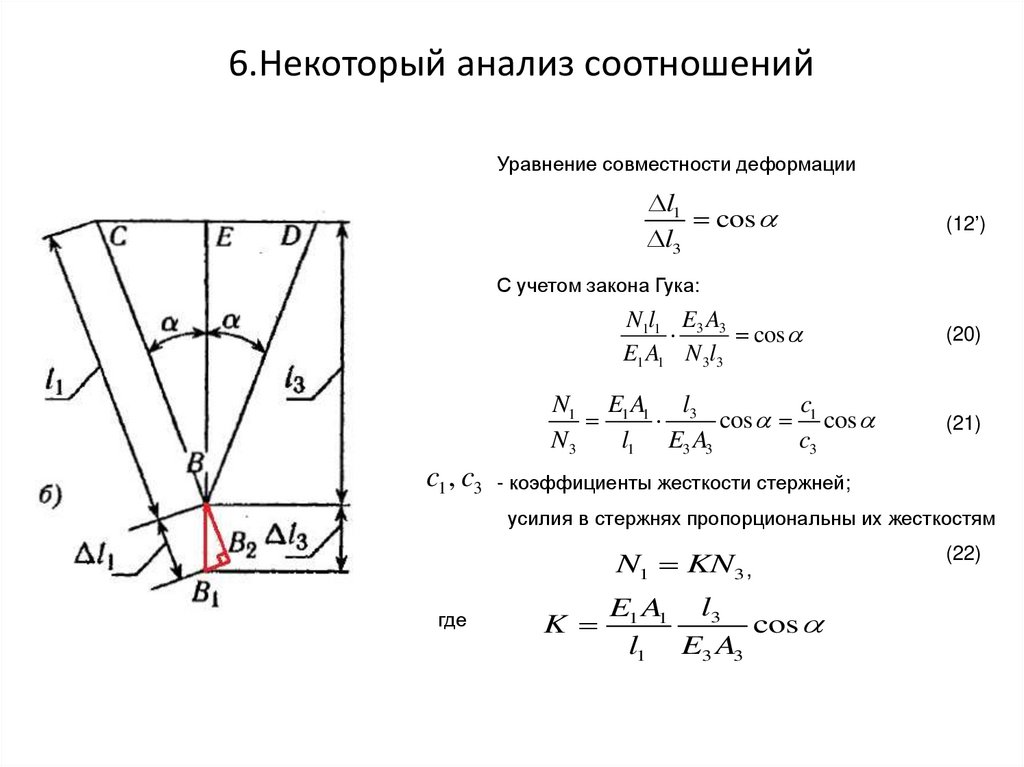
6.Некоторый анализ соотношенийУравнение совместности деформации
l1
cos
l3
(12’)
С учетом закона Гука:
N1l1 E3 A3
cos
E1 A1 N 3l3
(20)
N1 E1 A1 l3
c
cos 1 cos
N3
l1 E3 A3
c3
(21)
c1 , c3 - коэффициенты жесткости стержней;
усилия в стержнях пропорциональны их жесткостям
N1 KN3 ,
где
K
E1 A1 l3
cos
l1 E3 A3
(22)
10.
2 N1 cos N3 F 0(8’)
(22) -> (8′) =>
F
N3
1 2 K cos
KF
N1
1 2 K cos
(23)
10
11.
Расчет (подбор сечений) по методу допускаемыхнапряжений
(предельное упругое состояние)
(24)
Пусть
(25)
(20),(13),(14)
;
(26)
Нельзя подобрать сечения A1 и A3так, чтобы напряжения в них равнялись
допускаемым. Поэтому сначала подбирается сечение более нагруженного
стержня 3 согласно условию (предельное упругое состояние):
(27)
11
12.
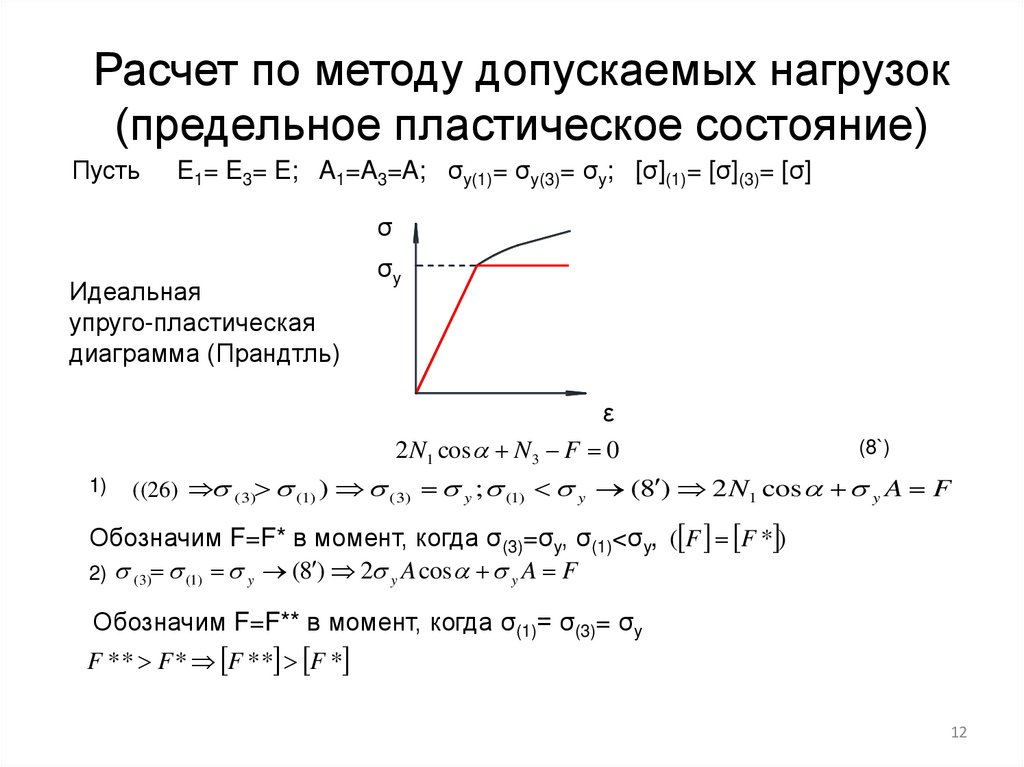
Расчет по методу допускаемых нагрузок(предельное пластическое состояние)
Пусть
E1= E3= E; A1=A3=A; σy(1)= σy(3)= σy; [σ](1)= [σ](3)= [σ]
σ
Идеальная
упруго-пластическая
диаграмма (Прандтль)
σy
ε
(8`)
2 N1 cos N 3 F 0
1) ((((26)
31) ( 3) (1) ) (3) y ; (1) y (8 ) 2 N1 cos y A F
Обозначим F=F* в момент, когда σ(3)=σy, σ(1)<σy, ( F F * )
2) ( 3) (1) y (8 ) 2 y A cos y A F
Обозначим F=F** в момент, когда σ(1)= σ(3)= σy
F * * F * F * * F *
12
13.
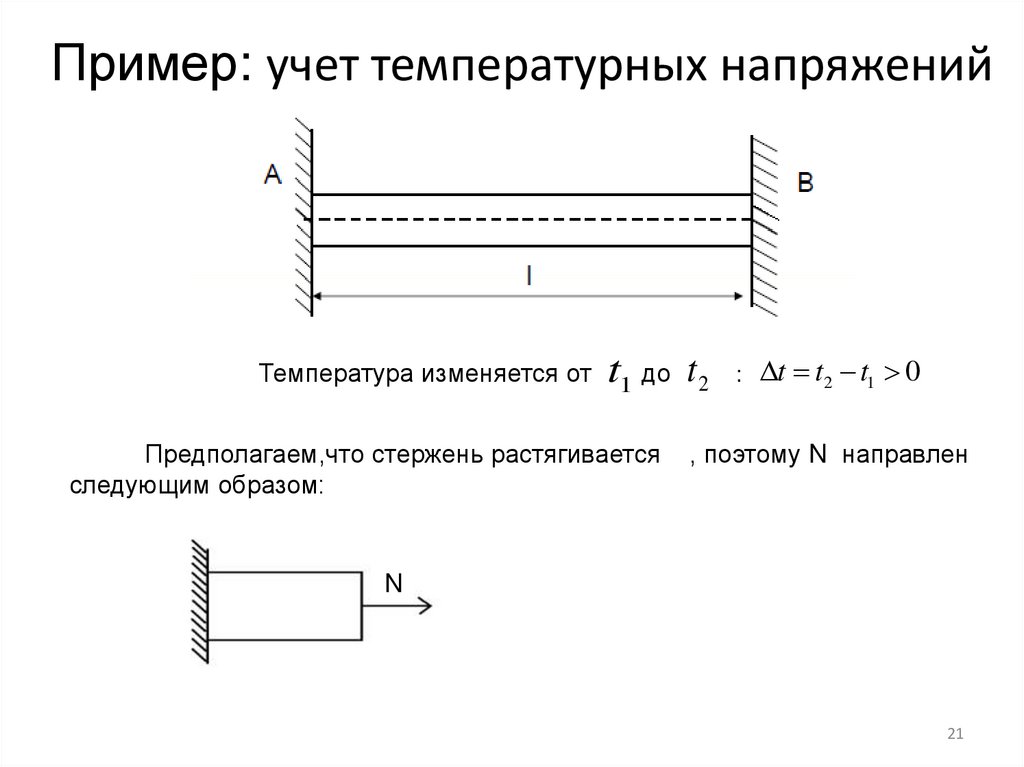
Неточности изготовления,учёт температурных деформаций
l j
N jl j
E j Aj
l j j t 0j j
(28)
t 0j 0 при нагревании, t 0j 0 при охлаждении
j - неточность изготовления
δj > 0, если длиннее номинала,
δj < 0, если короче номинала
βj – коэффициент линейного температурного расширения
13
14.
Рекомендации1. Предполагаем, что все стержни растягиваются. Если в
результате решения знак усилия отрицателен, это
означает, что предположение неверно (знак напряжения
будет вычислен верно).
2. Удлинение и укорочение определяются по диаграмме
совместности деформаций. При этом Δlj > 0, если
стержень становится длиннее; Δlj < 0, если короче.
3. Температурную деформацию и неточность изготовления
следует учитывать в уравнениях состояния (уравнениях
закона Гука).
14
15.
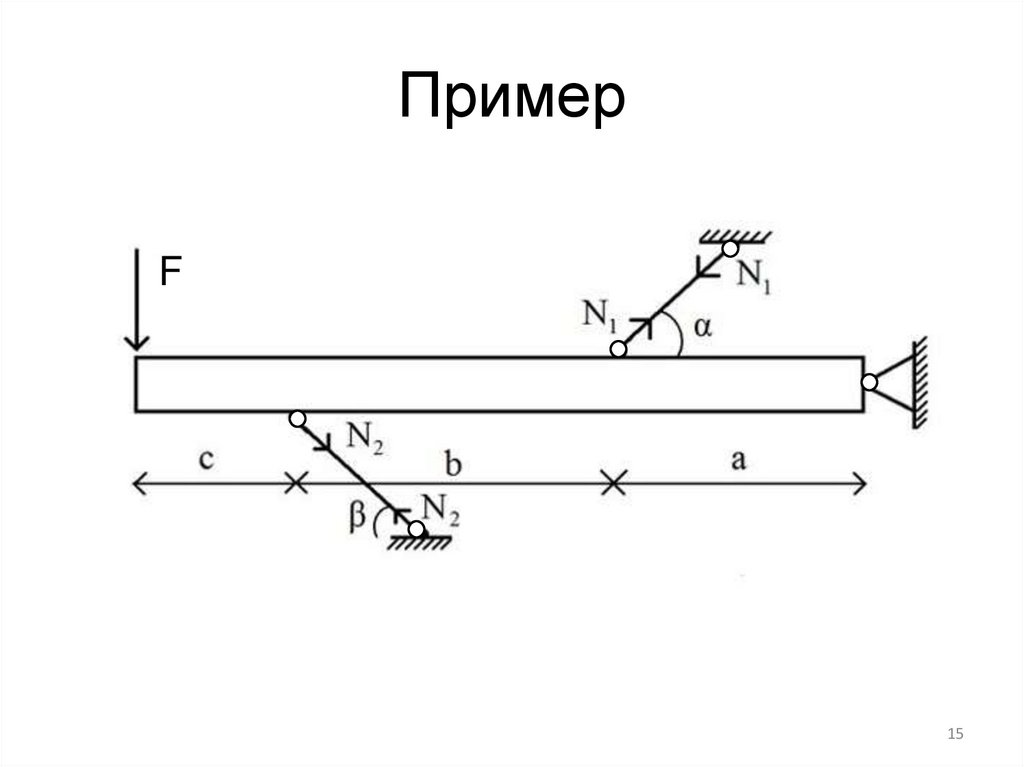
ПримерF
15
16.
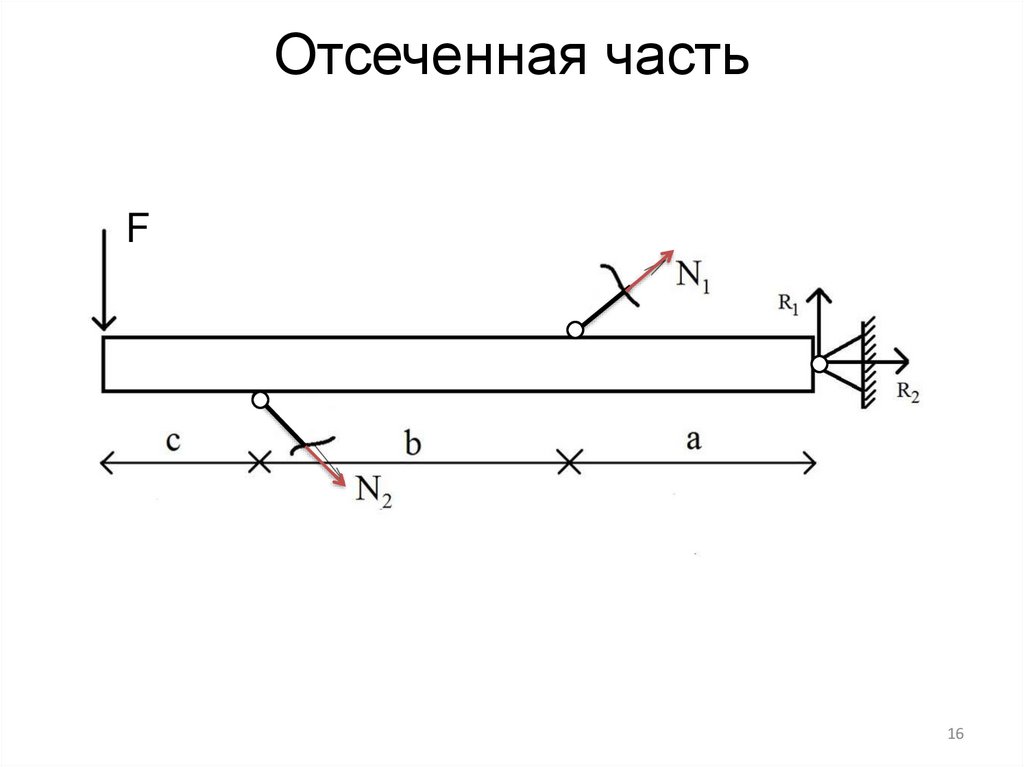
Отсеченная частьF
16
17.
Решение задачиУравнение равновесия отсеченной части
(29)
Почему не пишем
F 0; F 0 - ?
x
y
Степень статической неопределимости - ?
17
18.
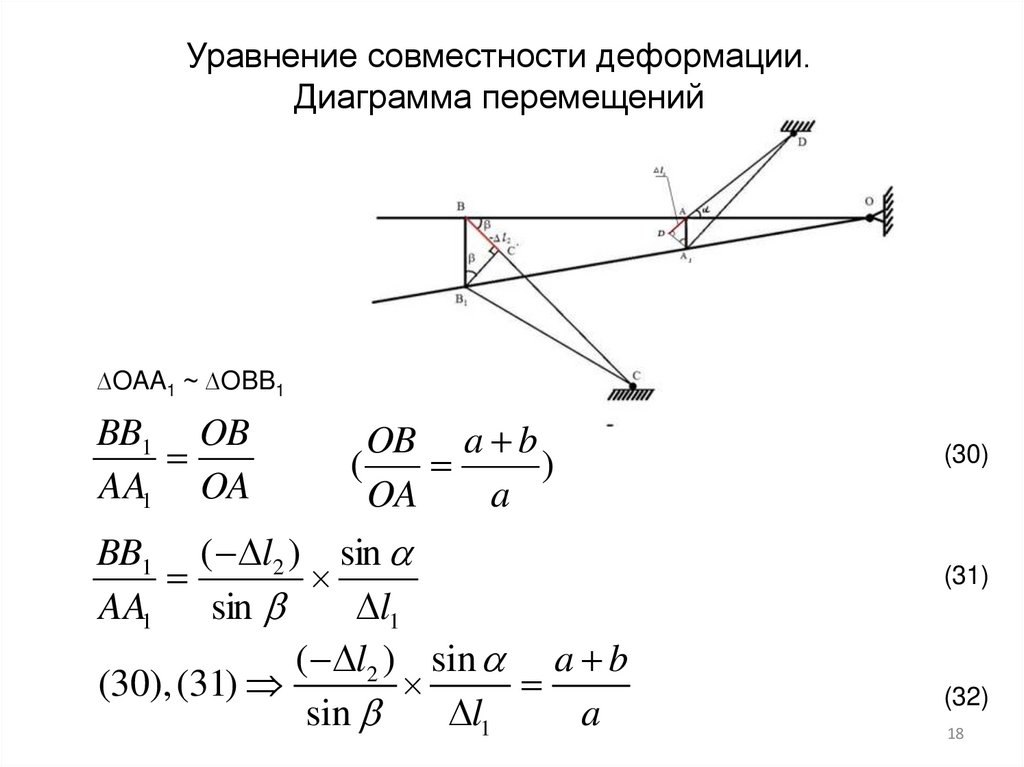
Уравнение совместности деформации.Диаграмма перемещений
∆OAA1 ~ ∆OBB1
BB1 OB
AA1 OA
OB a b
(
)
OA
a
BB1 ( l2 ) sin
AA1
sin
l1
( l2 ) sin a b
(30), (31)
sin
l1
a
(30)
(31)
(32)
18
19.
3. Определяющие уравнения (уравнения состояния)N 1l 1
N 2l2
l 1
l2
E 1 A1
E2 A2
(33)
(29), (32), (33) →




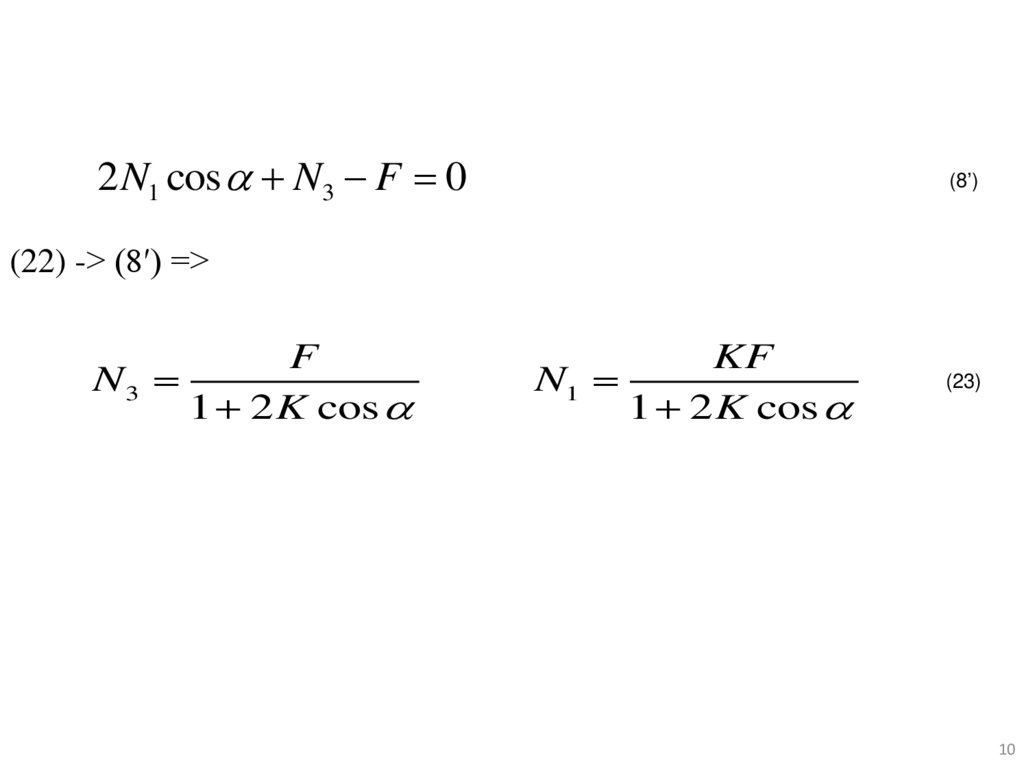









 mechanics
mechanics








