Similar presentations:
(1+1) өлшемді жергілікті емес Фокас-Ленеллс теңдеуінің солитондық шешімдерін модельдеу
1.
(1+1) өлшемді жергілікті емесФокас-Ленеллс теңдеуінің
солитондық шешімдерін
модельдеу
Тексерген:
Орындаған:
2.
План:• 1)
• 2)
• 3)
• 4)
3.
4.
5.
qxt − iqxx + 2qx − qxqr + iq = 0, (2)irxt − irxx − 2rx + rxrq + ir = 0, (3)
Фокас-Ленеллс жүйесінің [3] тривиальды емес ағынынан бастайық.
Oлар r = q∗ үшін FL теңдеуі (1)-ге дәл келтірілген, ал r = −q∗ таңдау сызықты емес мүшенің
таңбасының өзгеруімен (1) теңдеуге әкеледі. Қосылған FL теңдеуі (2) және (3) сәйкес келетін
Lax жұптары [3] түріндегі FL спектрлік есебімен берілуі мүмкін.
6.
∂xψ = (Jλ2 + Qλ)ψ = Uψ, (4)∂tψ = (Jλ2 + Qλ + V0 + V−1λ−1 + 1Jλ−2)ψ = V ψ, (5)
ψ=φ, J=−i 0, Q=0 qx,
φ
0 i
rx 0
i−1iqr0 01iq V0=2 1,V−1=12.
Мұндағы λ, ерікті комплекстік сан, меншікті мән (немесе изоспектрлік параметр) деп аталады, ал ψ FL жүйесінің λ-мен
байланысты өзіндік функция деп аталады. (2) және (3) теңдеулер Ut − Vx + [U, V ] = 0 (4) және (5) үйлесімділік шартына
баламалы.
Енді (4) және (5) спектрлік есеп үшін өлшеуіш түрлендірудің T матрицасын келесі түрде қарастырайық.
ψ[1] = T ψ,
ψ[1]x=U[1]ψ[1], U[1]=(Tx+TU)T−1. (7)
ψ[1]t=V[1]ψ[1], V[1]=(Tt+TV)T−1. (8)
(7) және (8) айқас дифференциалдау арқылы аламыз
U[1]t − V [1]x + [U[1],V [1]] = T(Ut − Vx + [U,V ])T−1. (9)
7.
Бұл (6) түрлендіру кезінде (2) және (3) теңдеулер инвариантты екенін дәлелдеу үшін U [1] жәнеV [1] бірдей пішіндерге ие болатындай T матрицасын құру өте маңызды екенін білдіреді. U
және V. Сонымен бірге U және V спектрлік матрицалардағы ескі потенциалдар (немесе
тұқымдық ерітінділер)(q, r) трансформацияланған спектрлік матрицалар тұрғысынан жаңа
потенциалдарға (немесе жаңа шешімдерге)(q[1], r[1]) бейнеленеді. U[1] және V[1]. Бұл жаңадан
алынған T матрицасы FL теңдеулер жүйесінің Дарбу түрлендіруі болып табылады. (2) және (3).
NLS[6, 7, 8] және DNLS[9, 10, 11] үшін DT негізінде, (6) теңдеудегі T сынақтық Darboux
матрицасы пішінде болады деп болжаймыз.
T1 =T1(λ;λ1;λ2)= a1 0 λ+ 0 b0 + a−1 0 λ−1
Мұнда a1, d1, b0, c0 анықталмаған коэффициенттер және олар (x, t) функциясы болып
табылады, олар FL спектрлік есепте λ1 және λ2-мен байланысты меншікті функциялар
арқылы өрнектелетін болады және a−1 және d−1 болады. тұрақтылар. Біздің әрі қарай
талдауымыз үшін екі меншікті функцияны ψj ретінде орнату
8.
олар FL спектрлік есепте λ1 және λ2-мен байланысты меншікті функциялар арқылыөрнектелетін болады және a−1 және d−1 болады. тұрақтылар. Біздің әрі қарай талдауымыз
үшін екі меншікті функцияны ψj ретінде орнату
ψj = φj , j = 1,2,φj = φj(x,t,λj), φj = φj(x,t,λj). (11)
Жалықтыратын, бірақ тура есептеулерден кейін біз FL жүйесінің бір еселенген Darboux
түрлендіруін аламыз
T (λ;λ ;λ )= a1λ+a−1λ−1 b0
содан кейін сәйкес жаңа шешімдер q[1] және r[1] келесі түрде беріледі:
q[1] =qa−1 + b0 ,r[1] =rd−1 + c0 .
d−1 d−1 a−1 a−1
a−1 = d−1 = 1 шартымен
9.
−1φ φ−1φ φ
−1φ
−λ
−λ
λ
φ
−λ
2 2 , d1 = 2
2 2 , b0 = 2 2 2
2,
1= 2
−1
c0 = λ2φ2 −λ2 φ2








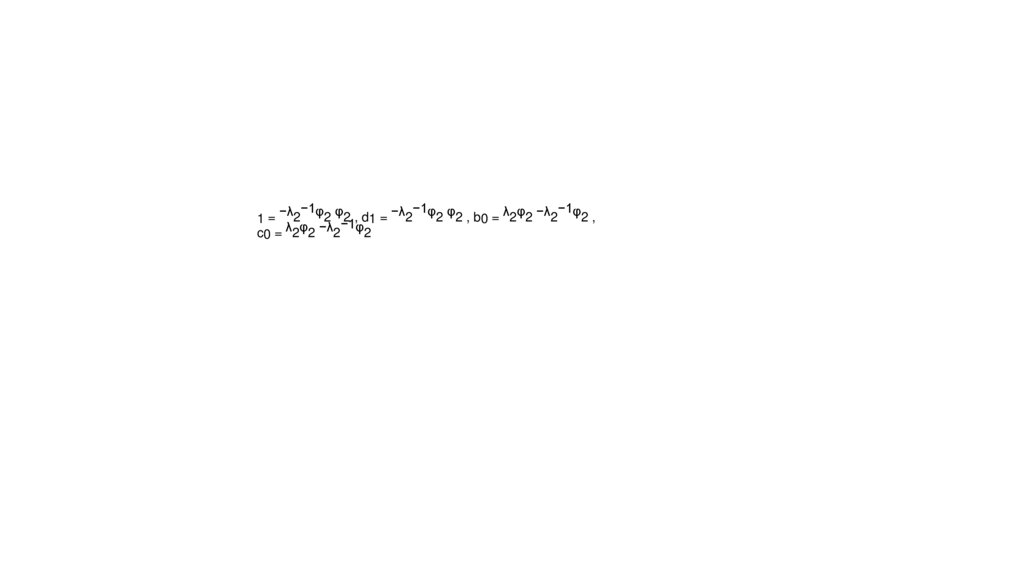

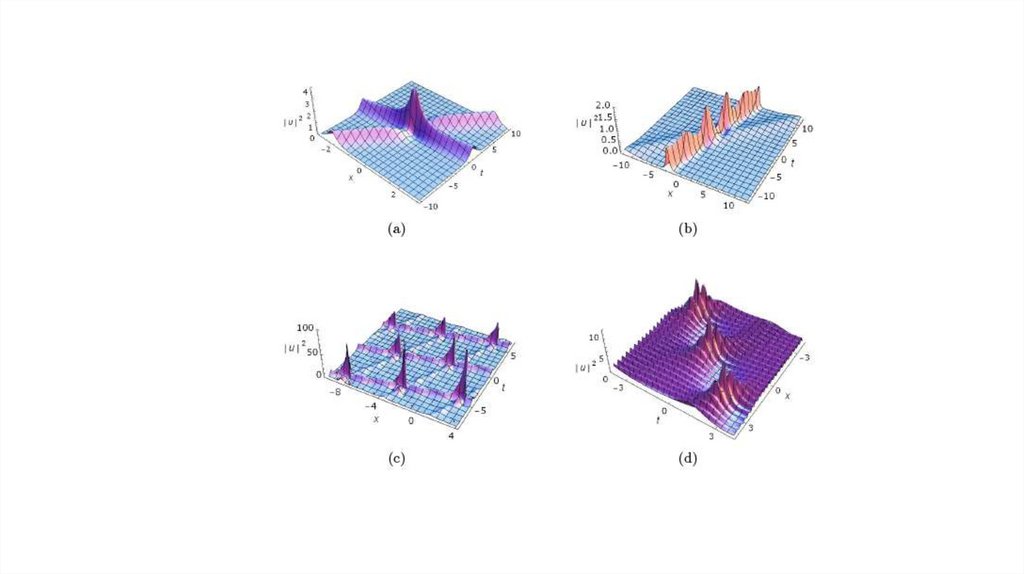
 physics
physics








