Similar presentations:
Формулы понижения степени
1. Тема урока: Формулы понижения степени.
2.
Вычислить:2
1
к )2 sin cos
sin
12
12
6 2
2
л) cos
sin
cos
8
8
4
2
2
2tg15
3
м)
2
tg 30
1 tg 15
3
3.
Применить формулы двойного аргументаsin 16x 2 sin 8x cos 8x
2
2
cos 8x cos 4 x sin 4 x
2 sin 7 x cos 7 x sin 14x
2
2
cos 3,5t sin 3,5t cos 7t
x
x
x
sin 2 sin cos
8
8
4
4.
cos2 х + sin2 х = 1;sin2 х = 1 – cos2 х;
cos 2x = cos2 х – sin2 х;
5.
cos2 х + sin2 х = 1;sin2 х = 1 – cos2 х;
cos 2x = cos2 х – sin2 х;
cos 2x = cos2 х – (1– cos2 х);
cos 2x = cos2 х – 1 + cos2 х;
cos 2x = 2 cos2 х – 1;
cos 2x + 1 = 2 cos2 х;
6.
cos2 х + sin2 х = 1;cos2 х = 1 – sin2 х
cos 2x = cos2 х – sin2 х;
7.
cos2 х + sin2 х = 1;cos2 х = 1 – sin2 х
cos 2x = cos2 х – sin2 х;
cos 2x = 1 – sin2 х – sin2 х;
cos 2x = 1 – 2 sin2 х;
cos 2x – 1 = – 2 sin2 х;
1 – cos 2x = 2 sin2 х;
8. Подумайте, какие возможности открываются перед нами с применением этих формул
Формулы понижения степени:Подумайте, какие
возможности открываются
перед нами с применением
этих формул
9. Итак, степень понижается за счет удвоения аргумента:
10. Вывод формулы понижения степени для тангенса и котангенса
Вывод формулы понижениястепени для тангенса и котангенса

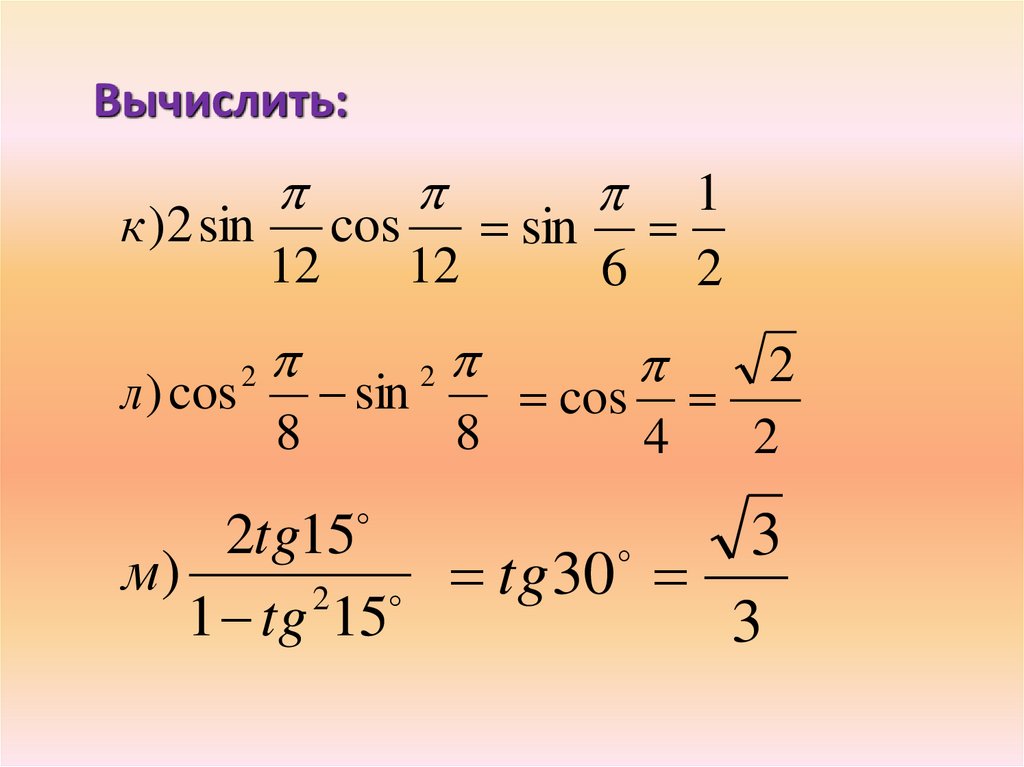


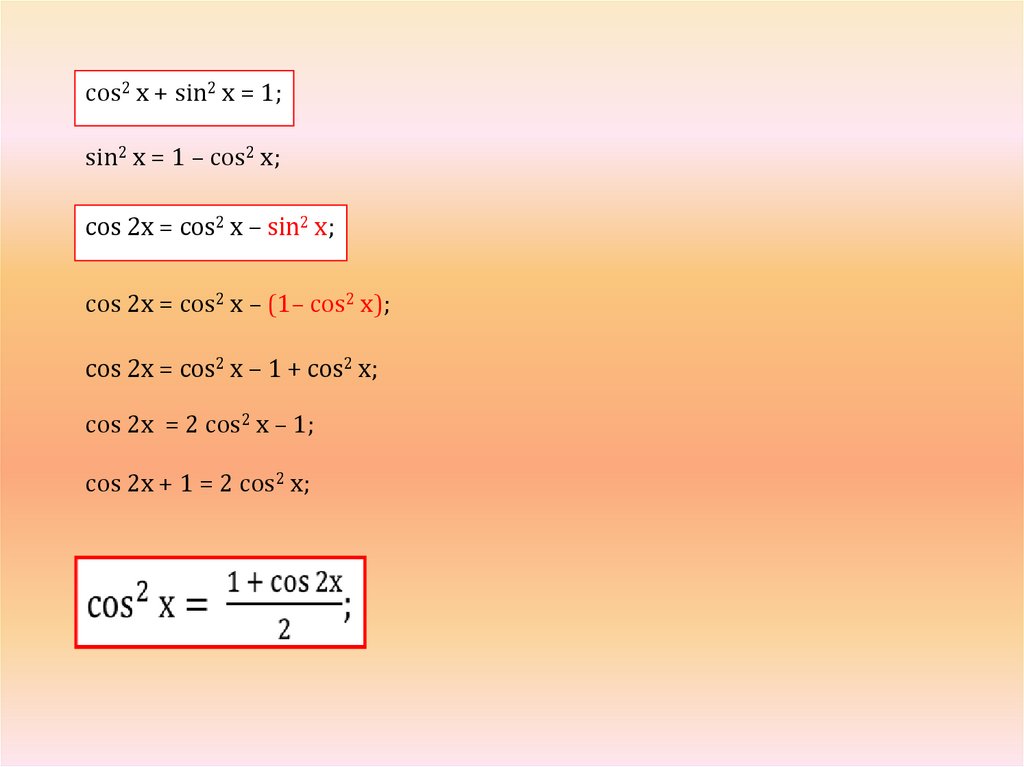

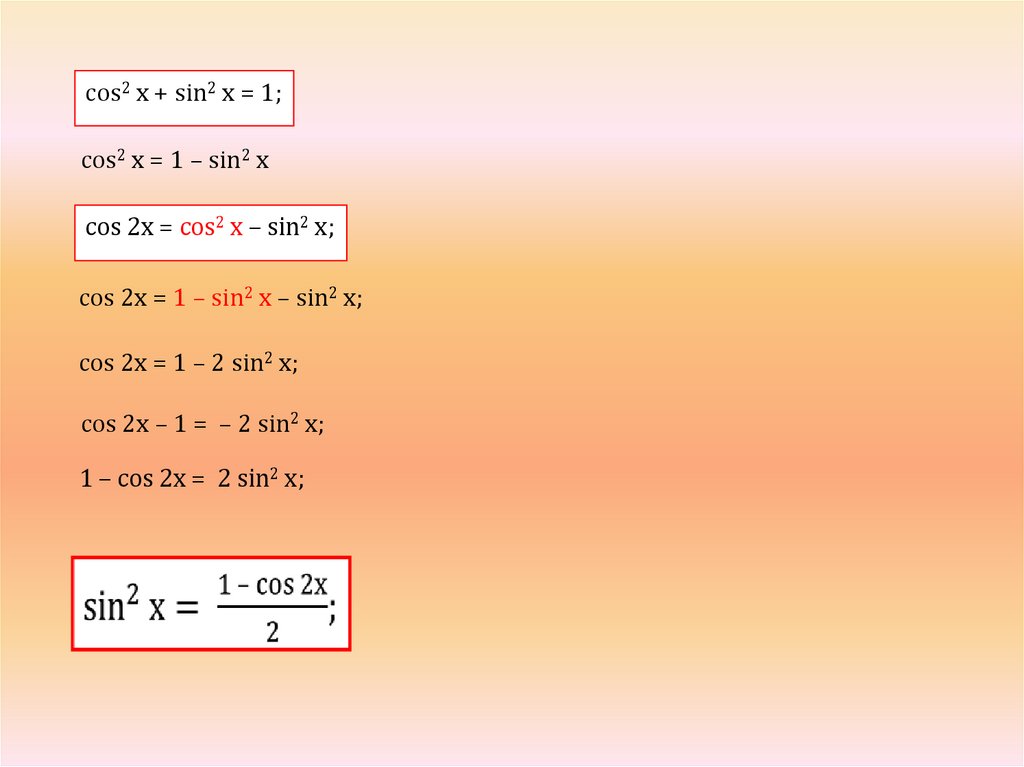







 mathematics
mathematics








