Similar presentations:
Турбулентное течение несжимаемого газа в канале, имеющем квадратное сечение
1.
Московский государственный университет имени М.В. ЛомоносоваОтчет о лабораторной работе по теме:
«Турбулентное течение несжимаемого газа в канале, имеющем квадратное сечение»
Выполнил:
студента группы СКТ-221
Кирков Даниил Игоревич
Саров 2021
2.
В качестве входного граничного условия задается дозвуковой вход спостоянной скоростью U= 10.0 м/с.
Свойства среды: плотность равна 1.205 кг/м3, молекулярная вязкость
1.85e-5 кг/(м с), температура T0=300oK.
В качестве исходных данных предоставлена сеточная модель расчетной
области – Файл – Task-14.mesh
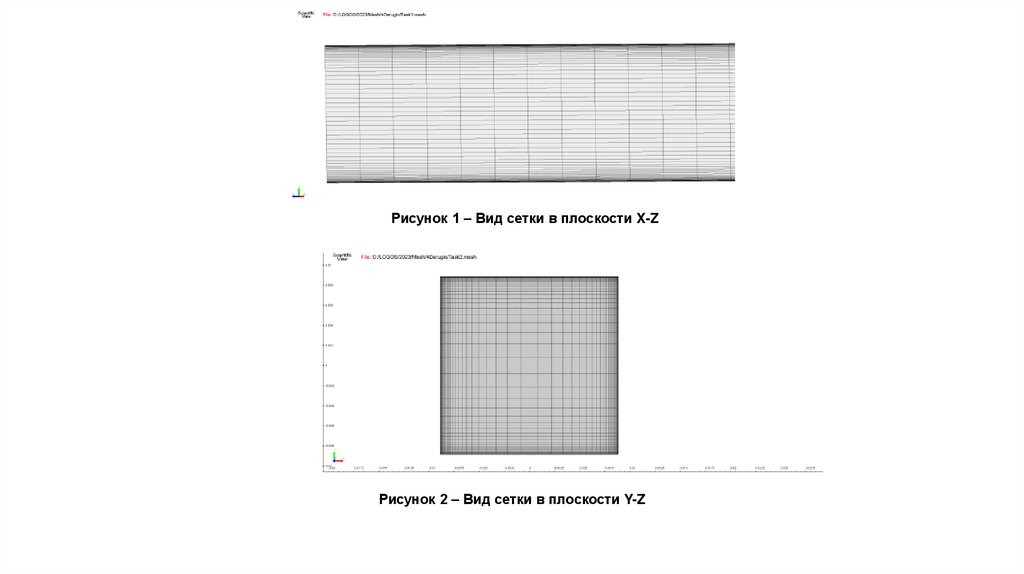
Общий вид сеточной модели представлен на рисунках 1-2.
3.
Рисунок 1 – Вид сетки в плоскости X-ZРисунок 2 – Вид сетки в плоскости Y-Z
4.
Состояние движущегося газа (или, в более общем случае – сплошной среды: жидкость, плазма) сизвестными термодинамическими свойствами определяется заданием скорости, плотности и давления
как функций координат и времени:
u t, r , t, r , P t, r
Для нахождения этих функций служит система уравнений газовой динамики, которая представляет
собой общие законы сохранения массы, импульса и энергии, выраженные в форме уравнений в
частных производных от зависимых величин (1.1):
div u 0
t
u
1
u u P
t
V
u V
u P
t
t
, P
1.2
1.3
1.4
(1.5)
Здесь
V
1
– удельный объём, т.е. объём, приходящийся на единицу
массы сплошной среды;
– удельная внутренняя энергия единицы массы.
5.
6.
Гипотеза Буссинеска для тензора Рейнольдса7.
8.
Модели турбулентности1. RANS модели:
• Секундова (v-92);
• SA Спаларта-Аллмараса: стандартная, скорректированная,…;
• k-e модели: стандартная, Чена, RNG, Realizable; модели для низких
чисел Рейнольдса
• k-w модели: стандартная, SST;
• q-w модель;
• V2f;
• ….
2. RSM модели
3. Модели крупных вихрей:
• LES;
• DES SA;
• DES SST;
• DDES SST.
9.
• Необходимо определить перепад давления между входной ивыходной границей.
Эмпирическое решение.
«Справочник по гидравлическим сопротивлениям» (1992), Идельчик И.Е.
Потери давления по длине прямой трубы (канала) постоянного
поперечного сечения (линейные
потери или потери на трение) вычисляются по формуле Дарси-Вейсбаха:
где
ρ — плотность среды, кг/м3;
v — характерная скорость, м/с;
— гидравлический диаметр, м;
— динамическая вязкость среды, Па·с или кг/(м·с);
10.
• Re = 11544,91) Движение жидкости при Re < 2300 будет устойчивое
ламинарное.
2) При Re > 2300 условии становится турбулентным (также его
называют неустойчивым турбулентным или переходным)
3) Устойчивый турбулентный характер поток жидкости приобретет
при Re > 10.000
11.
Потери давления по длине прямой трубы (канала) постоянногопоперечного сечения (линейные потери или потери на трение)
вычисляются по формуле Дарси-Вейсбаха:
Коэффициент сопротивления трения
Отношение потерь полного давления к динамическому давлению
12.
• Для области чисто турбулентного стабилизированного течения(Re > 4000) коэффициент сопротивления трения труб круглого
сечения с гидравлически (технически) гладкими стенками
определяют.
Для труб прямоугольного сечения поправочный коэффициент
коэффициента сопротивления, зависящий от отношения сторон а/b.
При турбулентном течении и a/b=1 поправочный коэффициент = 1
13.
Эмпирический перепад давленияΔP=107.879
14.
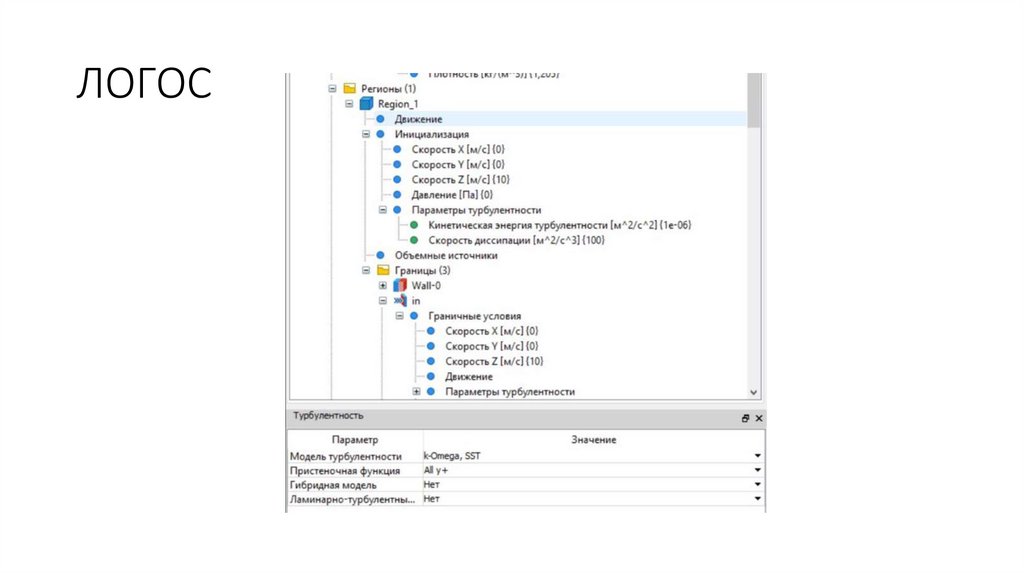
ЛОГОС15.
ЛОГОС16.
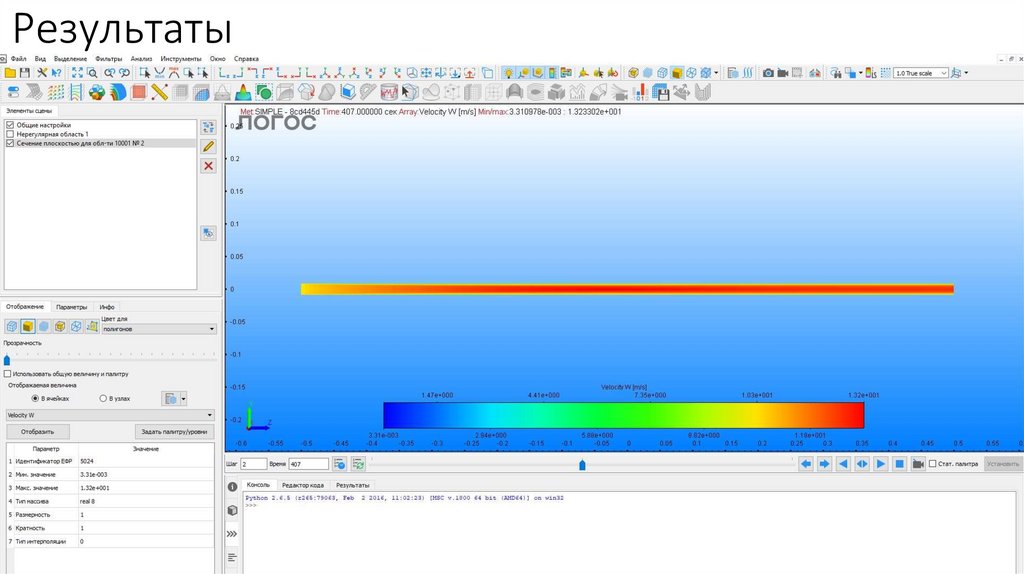
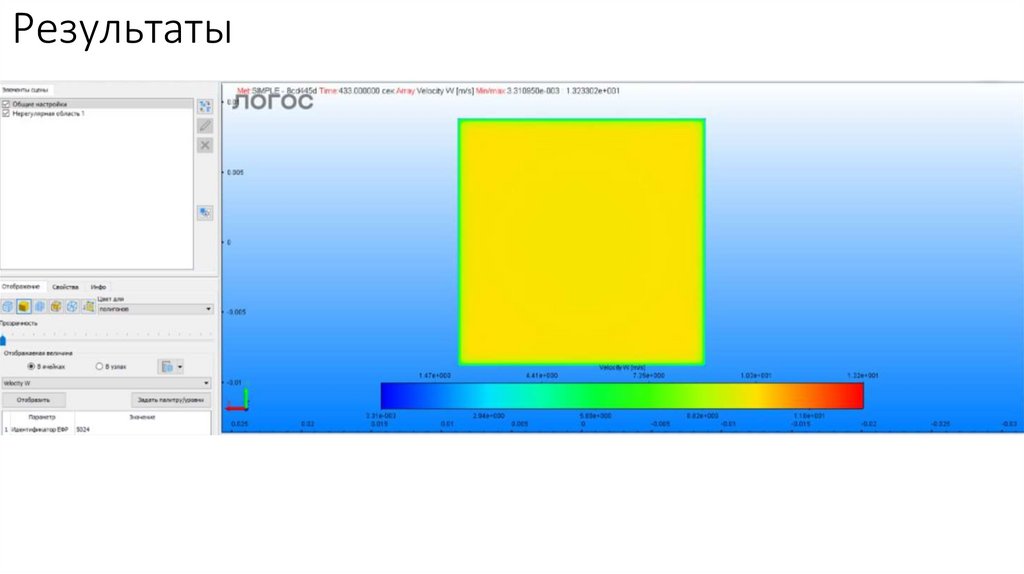
Результаты17.
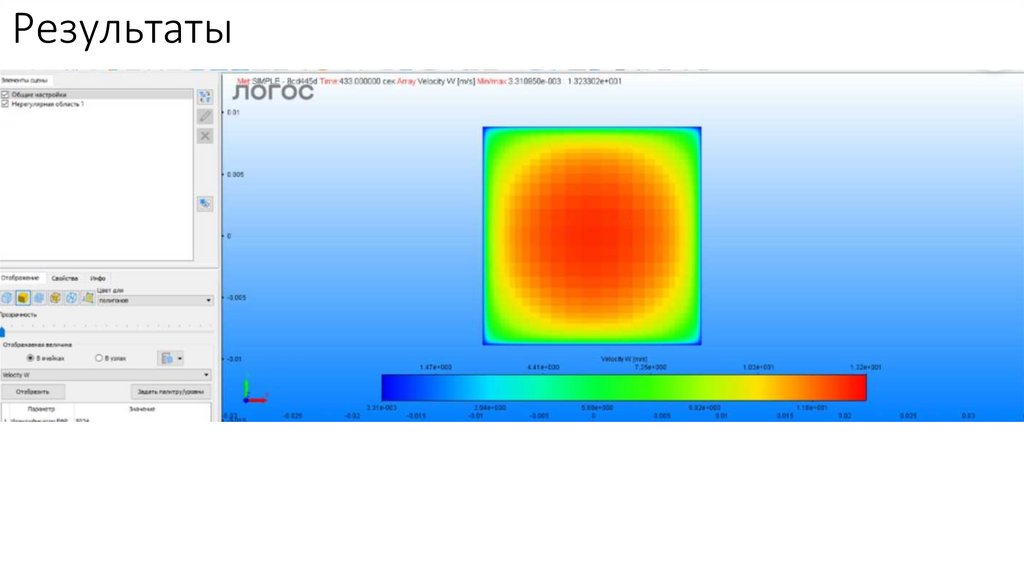
Результаты18.
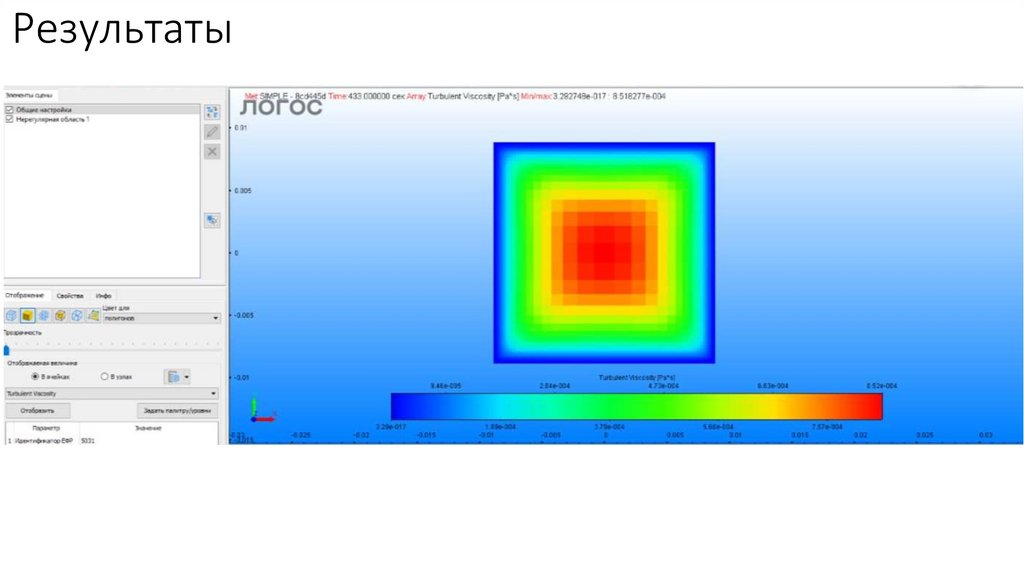
Результаты19.
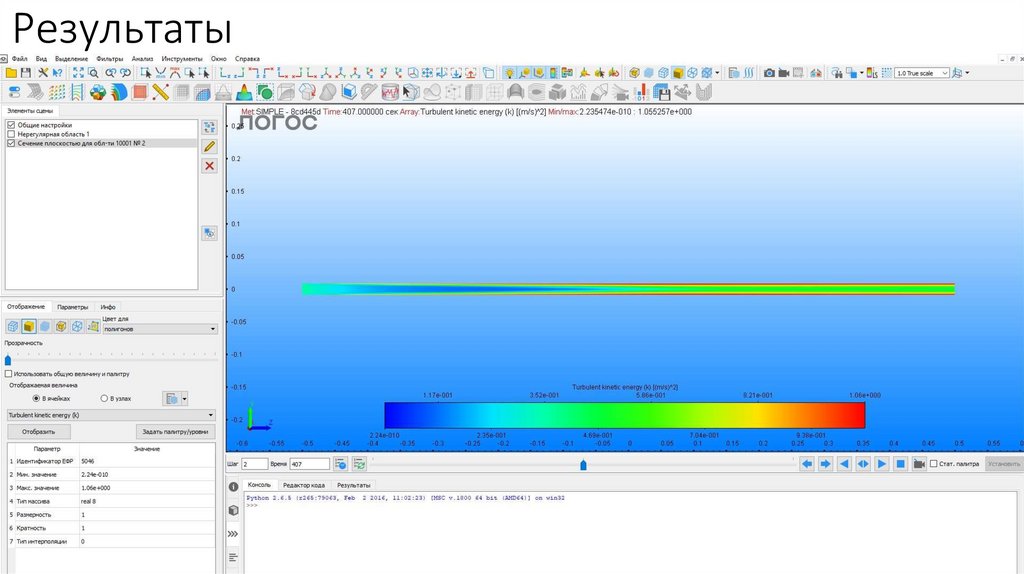
Результаты20.
Результаты21.
Результаты22.
Результаты23.
Результаты24.
Результаты25.
Результаты26.
27.
28.
ПОСТАНОВКА ЗАДАЧ ВНЕШНЕЙ АЭРОДИНАМИКИ• В общем виде течение вязкого сжимаемого газа описывается системой
уравнений Навье-Стокса, в интегральной форме выражающейся в виде
следующего закона сохранения:
28
29.
ПОСТАНОВКА ЗАДАЧ ВНЕШНЕЙ АЭРОДИНАМИКИ• Компоненты раскрываются следующим образом и описывают уравнения
сохранения массы, импульса и энергии:
29
30.
ПОСТАНОВКА ЗАДАЧ ВНЕШНЕЙ АЭРОДИНАМИКИ• Задачи аэродинамики описывают движение газообразной среды и её
силовые взаимодействия с твердыми телами.
• Внешняя аэродинамика – исследование потока вокруг твердых объектов
различной формы.
• Примеры: расчёт аэродинамики автомобиля, крыла самолета, полёта
снаряда.
• В задачах, как правило, требуется найти поле скоростей и воздействие
давления.
• Система также дополняется уравнением состояния рассматриваемого
газа, дающего связь между плотностью, давлением и температурой:





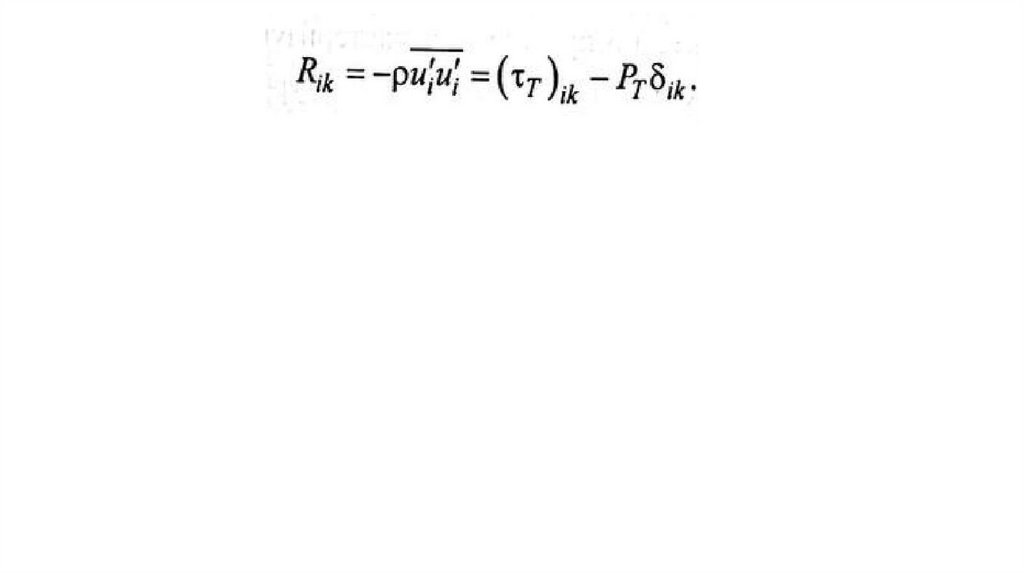


















 physics
physics








