Similar presentations:
Методы оценки и выбора альтернатив
1. Тема: МЕТОДЫ ОЦЕНКИ И ВЫБОРА АЛЬТЕРНАТИВ
2. 1.Понятие среды принятия управленческих решений
3. Концепция риска.
• Риск определяется каксостояния, когда известны
один или несколько исходов
по каждой альтернативе
и когда, вероятность
реализации каждого исхода
достоверно известна
лицу, принимающему
решение
4. Концепция определенности
Определенность – это такоесостояние, когда лицо,
принимающее решения,
заранее знает конкретный
исход для каждой
альтернативы
5. Концепция неопределенности
• Неопределенность – этокакое состояние знания,
когда одна или более
альтернатив имеют ряд
возможных исходов,
вероятность которых либо
неизвестна, либо не
имеет смысла.
6.
Методы выбора альтернатив вусловиях определенности
7.
Концепция определенностипод определенностью понимается такое состояние, когда ЛПР
заранее знает конкретный исход для каждой альтернативы
ПРЕДЕЛЬНЫЙ АНАЛИЗ
В условиях определенности доходы и затраты будут
известны для любого уровня производства и продаж
Задача предельного анализа состоит в том чтобы найти их
оптимальное соотношение позволяющее максимизировать
прибыль.
8.
Пример: топливная компанияФункция затрат исходя из динамики затрат и количества реализуемого
топлива : ТС = 1000 – 5Q + 0,05 Q2
- количество проданного топлива за неделю, тонн.
ТС – общие затраты за неделю
(по оси Х – количество, У – затраты (функция полиномы)
Находим MC – (первую производную от ТС) = -5 + 0,1 Q
где Q
Функция дохода Т R = 20 Q при постояной цене продажи 20 тыс. руб.
за тонну (при изменяющийся цене рассматривается динамика
дохода от цены и составляется уравнение линии тренда))
Находим MR – первую производную от TR
Оптимальный выпуск определяется из условия
МС = MR
-5 + 0,1 Q =20 Q = 250 т в неделю
9. Приростный анализ.
Приростной анализ прибыли оперирует с любыми ивсеми изменениями в доходах, затратах и
прибылях, явившимися следствием определенного
решения. Таким образом, концепция приростного
анализа охватывает изменения как самих
функций, так и их
значений. Основное
правило решения состоит
в том, чтобы принять
любое предложение,
повышающее прибыль,
или отвергнуть любое
предложение
10. Линейное программирование.
Модели линейного программирования отличаются наглядностьюи относительной простотой. Их использование во многих
практически важных задачах, связанных с принятием решений,
оказалось высокоэффективным, в связи с чем они получили
довольно широкое распространения. Наиболее известные задачи
линейного программирования:
задачи о распределении ограниченных ресурсов (задачи
оптимального планирования);
задачи об оптимальной корзине продуктов (задачи о диете,
задачи оптимального смешения);
задачи оптимального раскроя (материалов, заготовок);
транспортные задачи;
задачи о назначениях;
задачи оптимизации финансовых потоков;
задачи оптимизации графиков платежей.
11.
Предприятие может выпускать n видов продукции Р1, Р2,..., Рn,располагая для этого m различными ресурсами R1, R2,..., Rm в
количествах b1, b2,...bm соответственно. Известно, что для выпуска
единицы продукции Pj необходимо затратить аij единиц ресурса Rij,
i = 1, 2,..., m; j = 1, 2,..., n. Кроме того, известен доход от продажи
единицы каждого вида продукции – с1, с2,..., сn соответственно, где
cj – стоимость единицы продукта Рj например 1 штуки, 1 тонны и
т.п. Требуется так спланировать производственную программу –
объемы выпуска каждого вида продукции (в штуках, тоннах и т.п.),
чтобы максимизировать доход предприятия.
Необходимо найти совокупность значений {x1, х2, ... , хn},
обращающих в максимум целевую функцию
Z=c1x1 + c2x2 + … + cnxn
При условии, что переменные {x1, х2, ... , хn} удовлетворяют
системе ограничений:
а11x1 + a21x1 + ... + а1nхn≤ b1
а21x1 + a22x2 + ... + а2nхn≤
………….
amlx1 + am2x2 + ... + аmnхn≤ bm
12.
Пример. Предположим, что химический завод получил заказ на
производство 5000 кг специальной смеси из трех компонентов, состав
которой имеет следующие ограничения:
компонент 1:5 руб. за 1 кг, не более 1500 кг;
компонент 2: 6 руб. за 1 кг, не менее 750 кг;
компонент 3'. 7 руб. за 1 кг, но менее 1000 кг.
Какое количество каждого компонента должно быть использовано для
минимизации стоимости продукта?
Решение
Введем обозначения:
хх — количество компонента 1, кг;
х2 — количество компонента 2, кг;
х3 — количество компонента 3, кг.
Требуется минимизировать (целевая функция)
Z = 5х1 + 6х2 + 7х3
при условии, что
Х1 + х2 + хз> 5000,
X1 < 1500,
Х2 > 750,
х3 >1000,
Х\, Х2, х3 >0.
13.
• Для нашей задачи решением являютсяследующие величины: х, = 1500; х2 =
2500; х3 = 1000. Это означает, что цепь
минимизации стоимости будет
достигнута при использовании 1500 кг
компонента 1; 2500 кг компонента 2 и
1000 кг компонента 3.
• Обратите внимание, что эти значения
удовлетворяют каждому из наложенных
ограничений.
14. Методы выбора альтернатив в условиях риска
АльтернативыA1
A2
A3
…
S1
E
E
E
…
Состояние экономики
S2
S3
…
…
E
E
…
E
E
…
E
E
…
…
…
Матрица решенийA1, A2, A3 –альтернативные стратегии действий;
S1, S2, S3 – состояние эконо-мики (стабильность, спад, рост и др.);
E11; E12; E13; E21; … E33; … – результаты решений.
Числа в ячейках матрицы представляют собой результаты реализации Eij страте-гии Ai
в условиях Sj. При этом в условиях риска вероятность наступления Sj известна – wj(Sj).
Методы принятия решений в условиях риска используют теорию выбора, получившую название
теории полезности.
15. 2.Дерево решений.
Дерево решений строится с помощью пяти элементов:1. Момент принятия решения.
2. Точка возникновения события.
3. Связь между решениями и событиями.
4. Вероятность наступления события (сумма вероятностей в
каждой точке должна быть равна 1).
5. Ожидаемое значение (последствия) – количественное
выражение каждой альтернативы, расположенное в конце ветви.
Простейшее решение представляет собой выбор из двух
вариантов – «Да» или «Нет»
16.
17. Последовательность (дерево) принимаемых решений
18. Методы выбора альтернатив в условиях неопределенности
Если степень неопределенности слишком высока, топредпочитается не делать допущений относительно
вероятностей различных внешних условий, т.е. можно
не учитывать вероятности, или рассматривать их как
равные, что практически одно и то же. Если
применяется данный подход, то для оценки
предполагаемых стратегий имеются четыре критерия
решения:
а) критерий решения Вальда;
б) альфа-критерий решения Гурвица;
в) критерий решений Сэвиджа;
г) критерий решений Лапласа;
19. Критерий решения Вальда
Критерием Вальда «рассчитывай на худшее» (критерийкрайнего пессимизма или макси-мин) называют критерий,
предписывающий обеспечить значение параметра эффекта
равного α,
α = max min aij.
Этот критерий ориентирует ЛПР, на наихудшие условия и
рекомендует выбрать ту стратегию, для которой выигрыш
максимален. В других, более благоприятных условиях
использование этого критерия приводит к потере
эффективности системы или операции.
20.
Пример применения критерияВальда
Исходные данные.
Альтернативы
(Xi)
Состояния (j)
1
2
3
Х1
45
25
50
X2
20
60
25
21.
Пример применения критерия ВальдаЕсть два проекта Х1 и Х2, которые при трех возможных
сценариях развития региона (j=1..3) обеспечивают разную
прибыль. Значения прибыли приведены в таблице.
Необходимо выбрать проект для реализации.
Среди возможных проектов нет доминирующих ни абсолютно,
ни по состояниям. Поэтому решение придется принимать по
критериям.
Если выбор оптимального проекта осуществляется
по критерию Вальда, то ЛПР должен выполнить
следующие действия:
1. Найти минимальные исходы для каждой альтернативы. Это
и будут значения критерия Вальда:
W1 = min( x1j ), j = 1..3 => W1 = min(45, 25, 50) = 25
W2 = min( x2j ), j = 1..3 => W2 = min(20, 60, 25) = 20
2. Сравнить значения критерия Вальда и найти наибольшую
величину. Альтернатива с максимальным значением
критерия будет считаться оптимальной:
25 > 20 => W1 > W2 => X* = X1
22.
Альфа-критерий решения ГурвицаЭтот критерий рекомендует при выборе решения в
условиях неопределенности не руководствоваться ни
крайним пессимизмом (всегда «рассчитывай на худшее»,
α=0), ни крайним оптимизмом («все будет наилучшим
образом», α=1). Рекомендуется некое среднее решение (0≤ α
≤1). Этот критерий имеет вид
Н = max [α min eij +(1- α) max eij],
ijj
где α – некий коэффициент, выбираемый экспериментально
из интервала между
0 и 1.
Использование этого коэффициента вносит
дополнительный субъективизм в принятие решений с
использованием критерия Гурвица.
23.
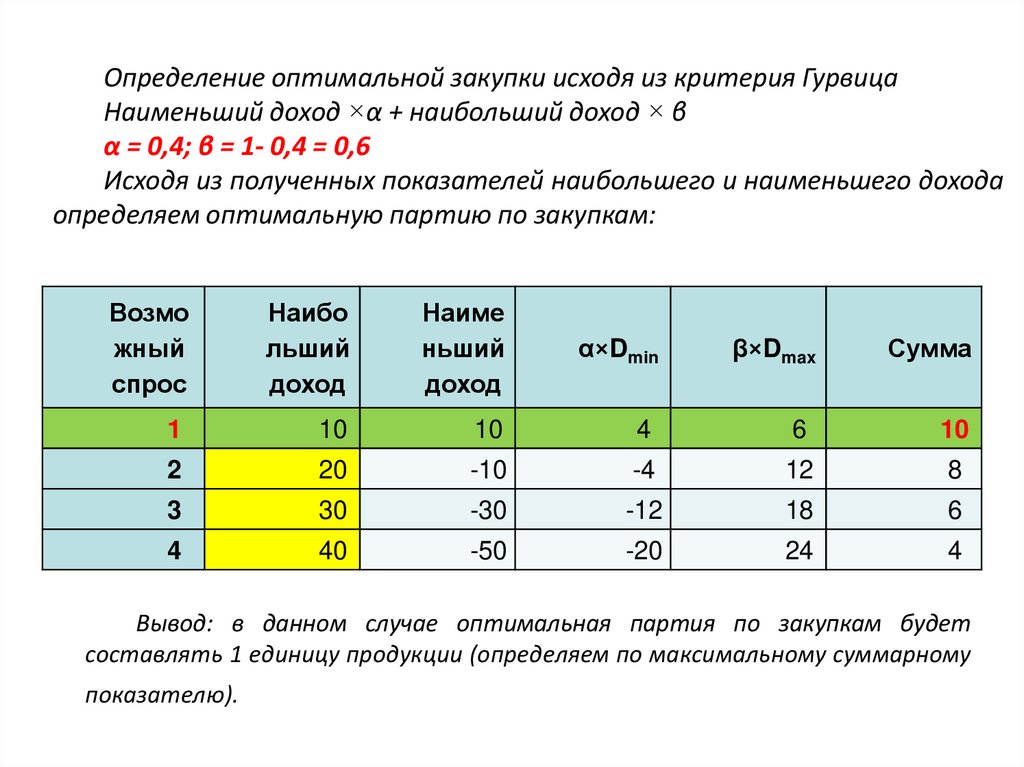
Определение оптимальной закупки исходя из критерия ГурвицаНаименьший доход ×α + наибольший доход × β
α = 0,4; β = 1- 0,4 = 0,6
Исходя из полученных показателей наибольшего и наименьшего дохода
определяем оптимальную партию по закупкам:
Возмо
жный
спрос
Наибо
льший
доход
Наиме
ньший
доход
α×Dmin
β×Dmax
Сумма
1
10
10
4
6
10
2
20
-10
-4
12
8
3
30
-30
-12
18
6
4
40
-50
-20
24
4
Вывод: в данном случае оптимальная партия по закупкам будет
составлять 1 единицу продукции (определяем по максимальному суммарному
показателю).
24. Критерий решения Сэвиджа
Минимаксный критерий Сэвиджа. В соответствии с этимкритерием, если требуется в любых условиях избежать большого
риска, то оптимальным будет то решение, для которого риск,
максимальный при различных вариантах условий, окажется
минимальным.
Критерий минимаксного риска Сэвиджа. При его использовании
обеспечивается наименьшее значение максимальной величины
риска:
S = min max rij,
ij
где риск rij определяется выражением: rij = βj - eij, β – максимально
возможный выигрыш.
Критерий Сэвиджа, как и критерий Вальда, – это критерий крайнего
пессимизма, но только пессимизм здесь проявляется в том, что
минимизируется максимальная потеря в выигрыше, по сравнению с
тем, чего можно было бы достичь в данных условиях.
25.
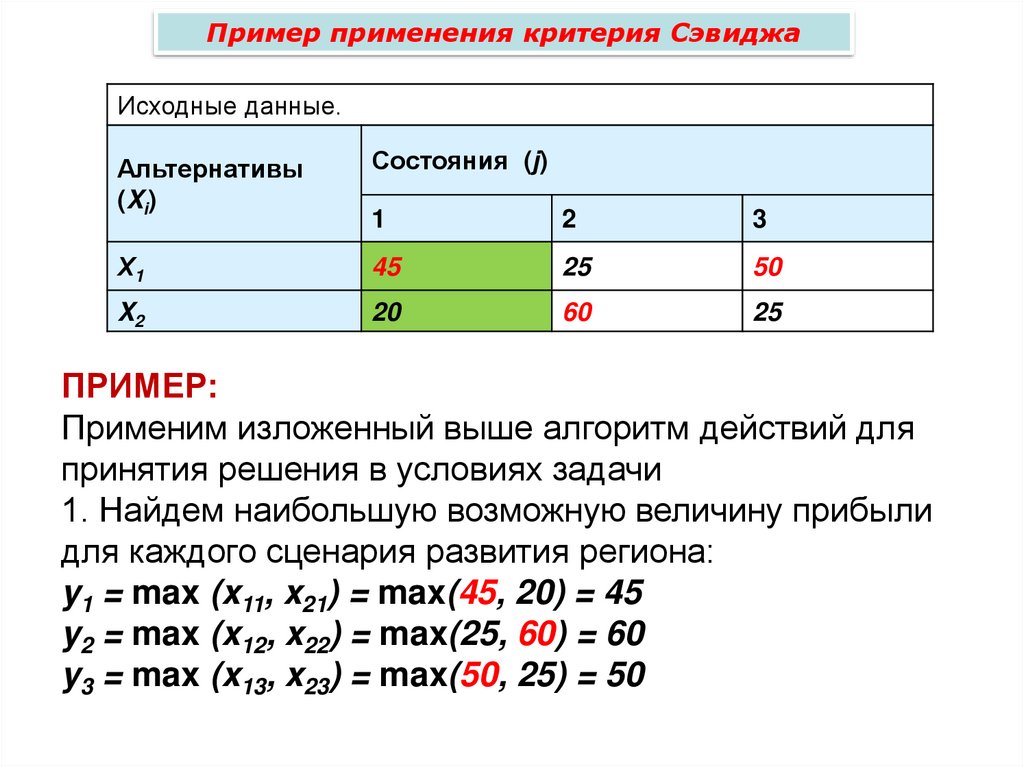
Пример применения критерия СэвиджаИсходные данные.
Альтернативы
(Xi)
Состояния (j)
1
2
3
Х1
45
25
50
X2
20
60
25
ПРИМЕР:
Применим изложенный выше алгоритм действий для
принятия решения в условиях задачи
1. Найдем наибольшую возможную величину прибыли
для каждого сценария развития региона:
y1 = max (x11, x21) = max(45, 20) = 45
y2 = max (x12, x22) = max(25, 60) = 60
y3 = max (x13, x23) = max(50, 25) = 50
26.
Рассчитаем значения "сожалений" для каждого проектапри каждом сценарии (т.е. найдем недополученную
прибыль по сравнению с максимально возможной при
данном сценарии развития). Составим из полученных
значений "матрицу сожалений".
для проекта Х1:
r11 = y1 - x11 = 45 - 45 = 0
r12 = y2 - x12 = 60 - 25 = 35
r13 = y3 - x13 = 50 - 50 = 0
для проекта Х2:
r21 = y1 - x21 = 45 - 20 = 25
r22 = y2 - x22 = 60 - 60 = 0
r23 = y3 - x23 = 50 - 25 = 25
27.
Альтернативы(Xi)
Макс.
"сожаление
" Si
Состояния природы (j)
1
2
3
X1
0
35
0
35
X2
25
0
25
25
yj
45
60
50
В полученной матрице по каждой строке найдем наибольшую величину
"сожаления" для каждого проекта. Это значение соответствует оценке
данной альтернативы по критерию Сэвиджа.
S1 = max(0, 35, 0) = 35
S2 = max(25, 0, 25) = 25
5. Сравним полученные величины и найдем проект с минимальным (!)
значением критерия. Он и будет оптимальным:
35 > 25 => S1 > S2 => X* = X2
ЛПР, руководствующийся при принятии решений критерием Сэвиджа,
выберет проект Х2.
28.
Рассмотрим выполнения на примере;Скоропортящийся продукт
Цена закупки - 50 тыс. руб. за ед.
Цена реализации - 60 тыс. руб. за ед.
Если продукт не продан, его цена в конце дня = 30 тыс. руб./ед.
Спрос в день, в среднем 1,2,3,4.
А. «Выбор оптимальной закупки исходя из дохода»
Определяем доход исходя из спроса и закупки продукта.
Спрос в
день
1
2
3
4
max
min
1
10
10
10
10
10
10
Возможность решения (закупки)
2
3
-10
-30
20
0
20
30
20
30
20
30
-10
-30
4
-50
-20
10
40
40
-50
29. Критерий решения Лапласа
Критерий Лапласа, гласит, что если вероятности состояниясреды неизвестны, то они должны приниматься как равные.
В этом случае выбирается стратегия, характеризующаяся самой
предполагаемой стоимостью при условии равных вероятностей.
Критерий Лапласа позволяет условие неопределенности сводить
к условиям риска. Критерий Лапласа называют критерием
рациональности, и он подходит для стратегических
долгосрочных решений, как и все вышеназванные критерии.
Кроме вышеназванных четырех критериев, для принятия решений в условиях
неопределенности существуют неколичественные методы, такие как
приобретение дополнительной информации, хеджирование, гибкое
инвестирование и др.
30.
Критерий Лапласа основан на принципе недостаточногообоснования. Поскольку в рамках информационного подхода в
ситуации неопределенности вероятности состояний неизвестны,
то нет оснований утверждать, что они различны. Поэтому можно
допустить, что они одинаковы.
По критерию Лапласа в качестве оценки альтернативы
используется средний выигрыш:
Оптимальной является альтернатива с максимальным
средним выигрышем:
Х* = Хk, Lk = max(Li), i = 1..N
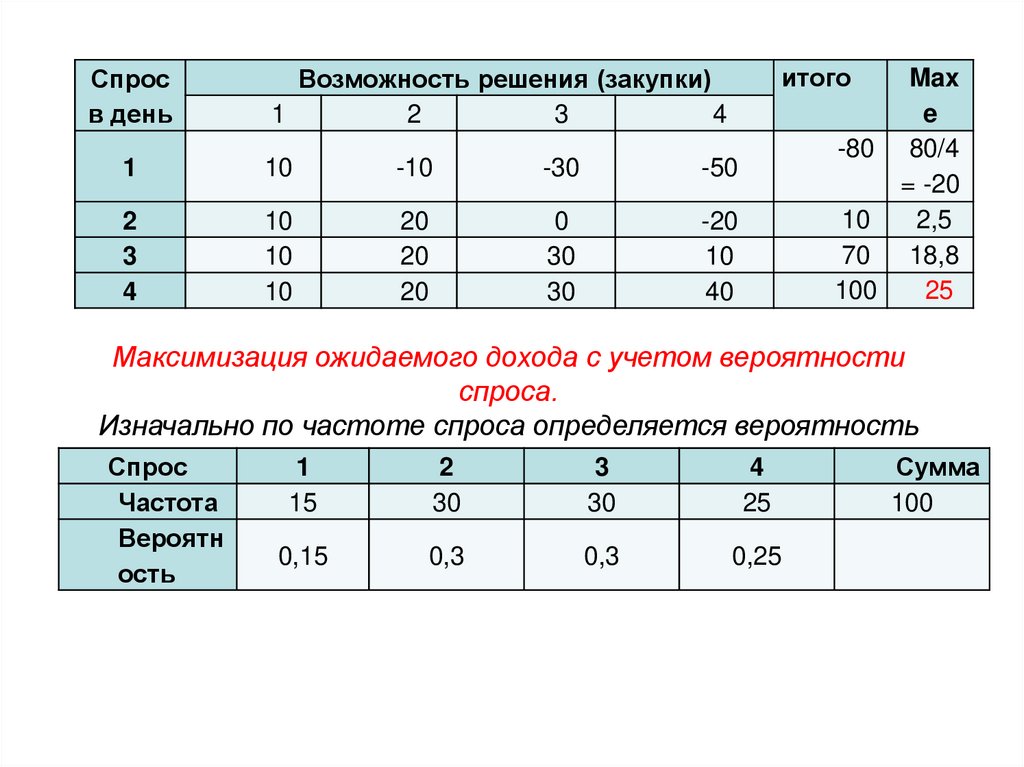
31.
Спросв день
итого
Возможность решения (закупки)
1
2
3
4
1
10
-10
-30
-50
2
3
4
10
10
10
20
20
20
0
30
30
-20
10
40
Max
e
-80 80/4
= -20
10
2,5
70
18,8
100
25
Максимизация ожидаемого дохода с учетом вероятности
спроса.
Изначально по частоте спроса определяется вероятность
Спрос
Частота
Вероятн
ость
1
15
2
30
3
30
4
25
0,15
0,3
0,3
0,25
Сумма
100
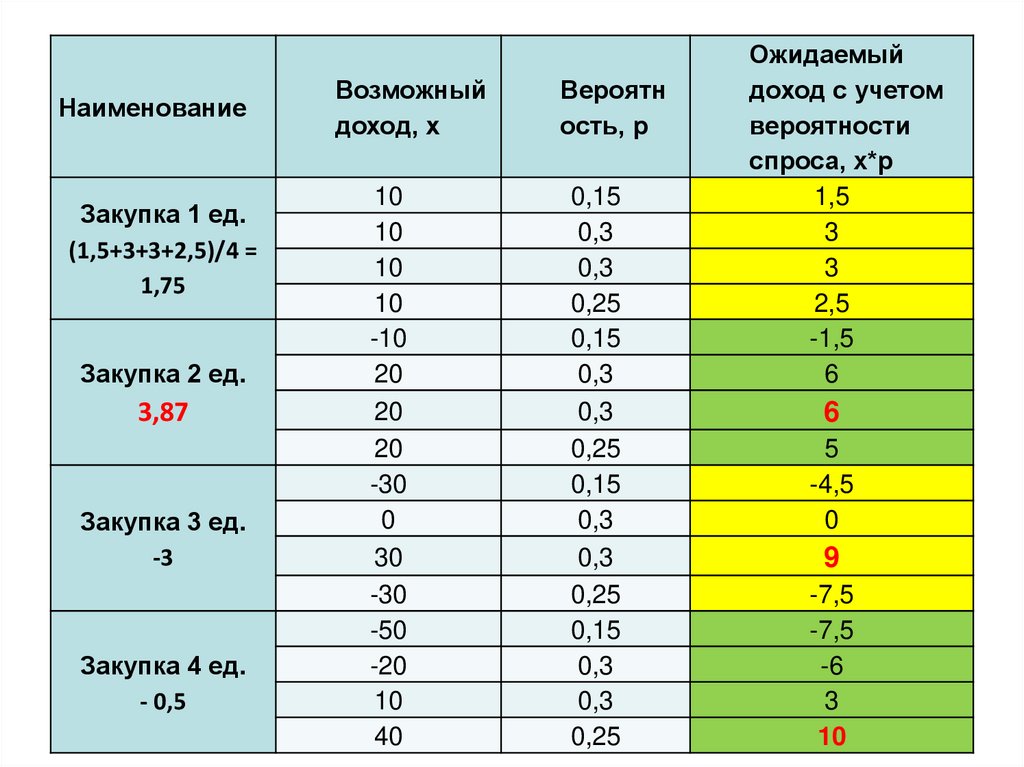
32.
НаименованиеЗакупка 1 ед.
(1,5+3+3+2,5)/4 =
1,75
Закупка 2 ед.
3,87
Закупка 3 ед.
-3
Закупка 4 ед.
- 0,5
Возможный
доход, х
10
10
10
10
-10
20
20
20
-30
0
30
-30
-50
-20
10
40
Вероятн
ость, р
0,15
0,3
0,3
0,25
0,15
0,3
0,3
0,25
0,15
0,3
0,3
0,25
0,15
0,3
0,3
0,25
Ожидаемый
доход с учетом
вероятности
спроса, х*р
1,5
3
3
2,5
-1,5
6
6
5
-4,5
0
9
-7,5
-7,5
-6
3
10
33. Экспертные методы
1.Экспертные оценки – этокачественные оценки, основанные на
информации неколичественного
(качественного) характера, которые
могут быть получены только с
помощью специалистов – экспертов.
Эксперт – это
высококвалифицированный
специалист, полагающийся на свои
знания, опыт, интуицию и умение
оценивать сложные факторы (явления)
и способный создать собственную
обоснованную (интуитивную) модель
анализируемого явления (проблемы).
34. 1.определение состава возможных событий в какой-либо системе в определенном интервале времени; 2. определение вероятностей
1.определение состава возможных событий в какойлибо системе в определенном интервале времени;2. определение вероятностей событий и временных
интервалов во множестве событий;
3. структурирование проблемного поля организации
и определение приоритетности решения проблем;
4. дифференциация целей управления до задач и
определение приоритетности их решения;
5.генерирование альтернатив;
6.фильтрация множества альтернатив и оценка их
предпочтительности.
35.
2.Экспертные суждения – содержательные высказывания(определяющие состав, структуру, функциональность исследуемой
системы, сущностей и их атрибутов), количественная или
качественная оценка какой-либо сущности (т.е. определение
количественных и качественных атрибутов и их значений).
36.
• Экспертное ранжирование. Ранжированиеприменяется в случаях, когда невозможна
или нецелесообразна непосредственная
оценка. При этом ранжирование объектов
содержит лишь информацию о том, какой из
них более предпочтителен, и не содержит
информации о том, насколько или во сколько
раз один объект предпочтительнее другого.
37.
• Ранг – степень отличия по какому-либопризнаку, а ранжирование – процесс
определения рангов, относительных
количественных оценок степеней
отличий по качественным признакам.
38.
Метод простой ранжировки.Заключается в том, что эксперты располагают
объекты ранжирования (например, критерии) в
порядке убывания их значимости (скажем, для
альтернатив это убывание
предпочтительности). Ранги обозначаются
цифрами от 1 до п, где п – количество рангов.
Сумма рангов Sn при этом будет равна сумме
чисел натурального ряда:
Sn= n(n+1) : 2

































 management
management








