Similar presentations:
Теория принятия решений в условиях риска и неопределенности
1. Теория принятия решений в условиях риска и неопределенности
LOGO2. Типы неопределенности
В случае если лицо, принимающее решение,имеет лишь представление о возможных
вариантах развития событий в будущем, то
говорят о принятии решения в условиях
полной неопределенности
Если лицо, принимающее решение, имеет не
только представление о возможных вариантах
развития событий в будущем, но и имеет
объективные оценки вероятностей реализации
различных сценариев будущего, то говорят о
принятии решения
в условиях риска
3. Особенности принятия решения
наличие не менее двухвзаимоисключающих вариантов, из
которых должен быть выбран только
один
наличия критерия, позволяющего
количественно оценивать имеющиеся
варианты, и по этим оценкам
осуществлять выбор
4. Этапы исследования задач принятия решений
1-й этап - построение математическоймодели ЗПР
2-й этап — формулировка принципа
оптимальности и нахождение
оптимального решения
3-й этап - анализ полученных
результатов
5. Принятие решений в условиях неопределенности
LOGO6. 1-й этап: построение математической модели ЗПР
Набор объектов < X, Y, F > составляетреализационную структуру задачи принятия
решения, где
X – множество допустимых вариантов
(решений) (контролируемые факторы)
Y – множество возможных состояний среды
(неконтролируемые факторы)
F: X x Y R – целевая функция
(математический эквивалент цели операции)
7. Пример 1
Энергетическая компания должна выбрать проектэлектростанции. Всего имеется 4 типа электростанций: А1 —
тепловые, А2 — приплотинные, А3 — бесшлюзовые, А4 —
шлюзовые.
Последствия, связанные со строительством и дальнейшей
эксплуатацией электростанции каждого из этих типов,
зависят от ряда неопределенных факторов (состояния
погоды, возможности наводнения, цены топлива, расходы по
транспортировке топлива и т.п.).
Предположим, что можно выделить четыре варианта
сочетаний данных факторов — они выступают в качестве
состояний среды и обозначаются здесь через В1, В2, В3, В4.
Экономическая эффективность электростанции
определяется в данном случае как процент прироста дохода
в течение одного года эксплуатации электростанции в
сопоставлении с капитальными затратами; зависит как от
типа электростанции, так и от состояния среды и
определяется следующей таблицей
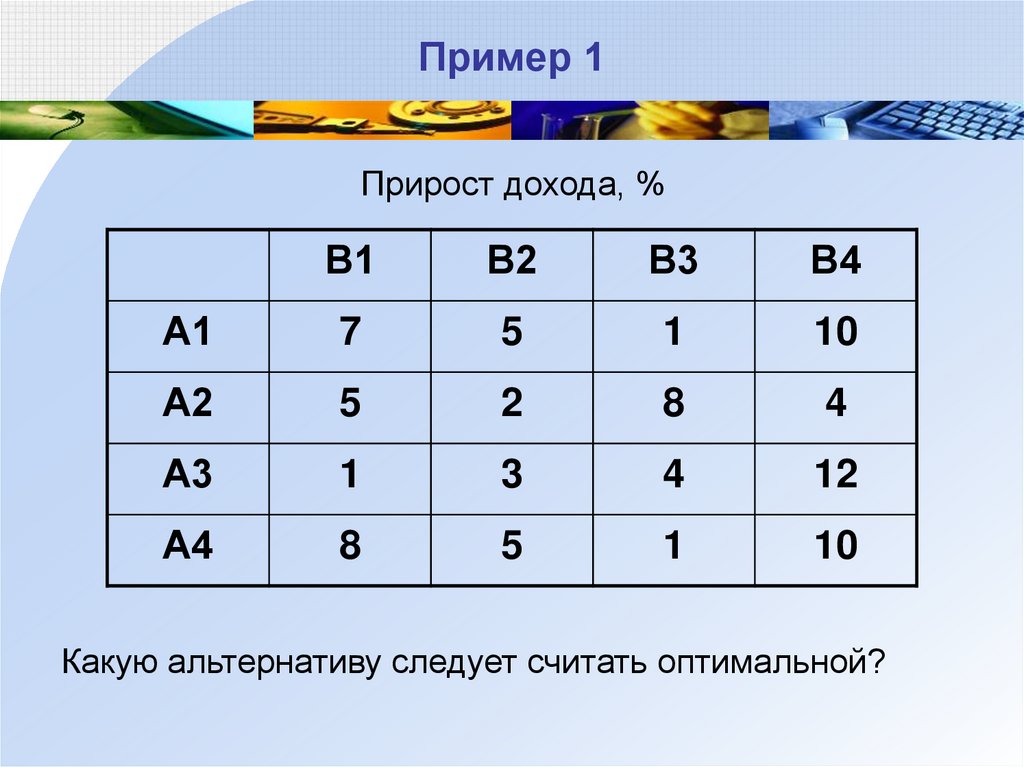
8. Пример 1
Прирост дохода, %В1
В2
В3
В4
А1
7
5
1
10
А2
5
2
8
4
А3
1
3
4
12
А4
8
5
1
10
Какую альтернативу следует считать оптимальной?
9. Принцип доминирования
Говорят, что альтернатива i1 доминируетальтернативу i2 ( i1 i2 ), если при любом
состоянии среды выигрыш принимающего
решение при выборе им альтернативы i1 будет
не меньше, чем его выигрыш при выборе
альтернативы i2 , т. е. выполняется условие
ai1 ai2 , при всех j 1,..., m
j
j
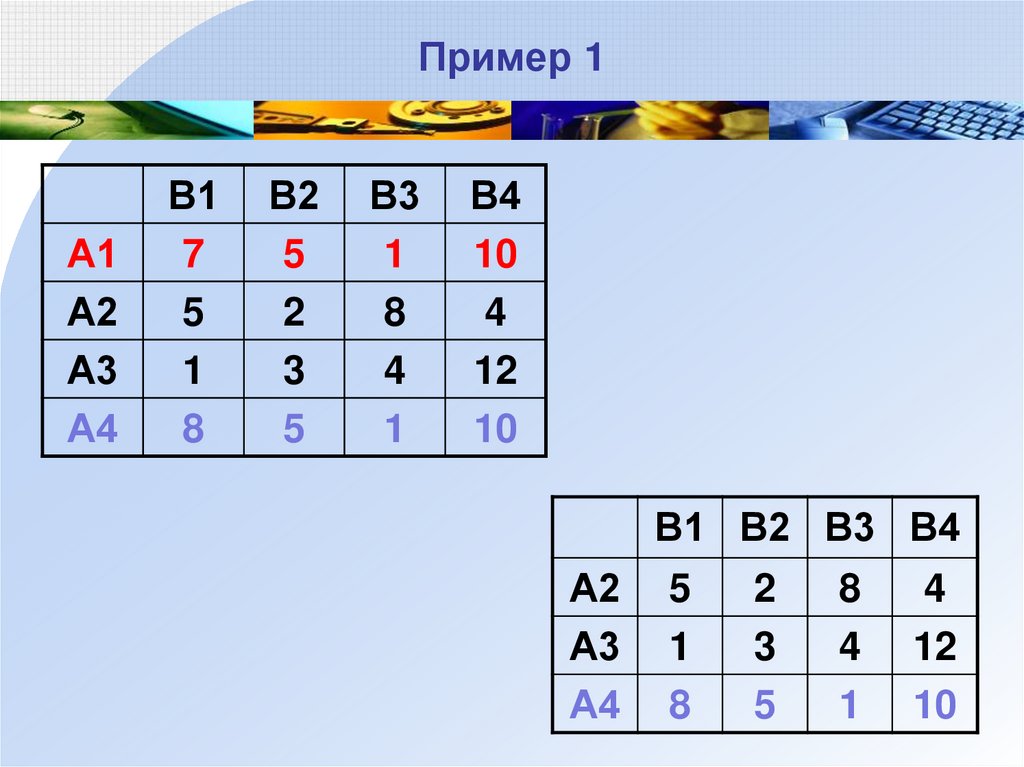
10. Пример 1
А1А2
А3
А4
В1
7
5
1
8
В2
5
2
3
5
В3
1
8
4
1
В4
10
4
12
10
В1 В2 В3 В4
А2
А3
А4
5
1
8
2
3
5
8
4
1
4
12
10
11. Основной метод выбора оптимальной альтернативы
Формулируется некоторая гипотеза оповедении среды, позволяющая дать
каждой альтернативе единую числовую
оценку
Оптимальной будет та альтернатива, которая
является наиболее предпочтительной, то есть
имеет наибольшую числовую оценку (для
случая функции потерь — наименьшую
числовую оценку)
12. Типы критериев
Критерий Вальда(гарантированного результата)
Критерий Лапласа
Критерий Сэвиджа
Критерий Гурвица
13. Критерий Вальда
Гипотеза: "При выборе решения надорассчитывать на самый худший
возможный вариант"
14.
Задача на maxОценка альтернативы:
W (i) min ai
j
j
Оптимальная стратегия:
W (i ) max W (i) max min ai
*
i
i
j
j
15.
Задача на minОценка альтернативы:
W (i) max ai
j
j
Оптимальная стратегия:
W (i ) min W (i) min max ai
*
i
i
j
j
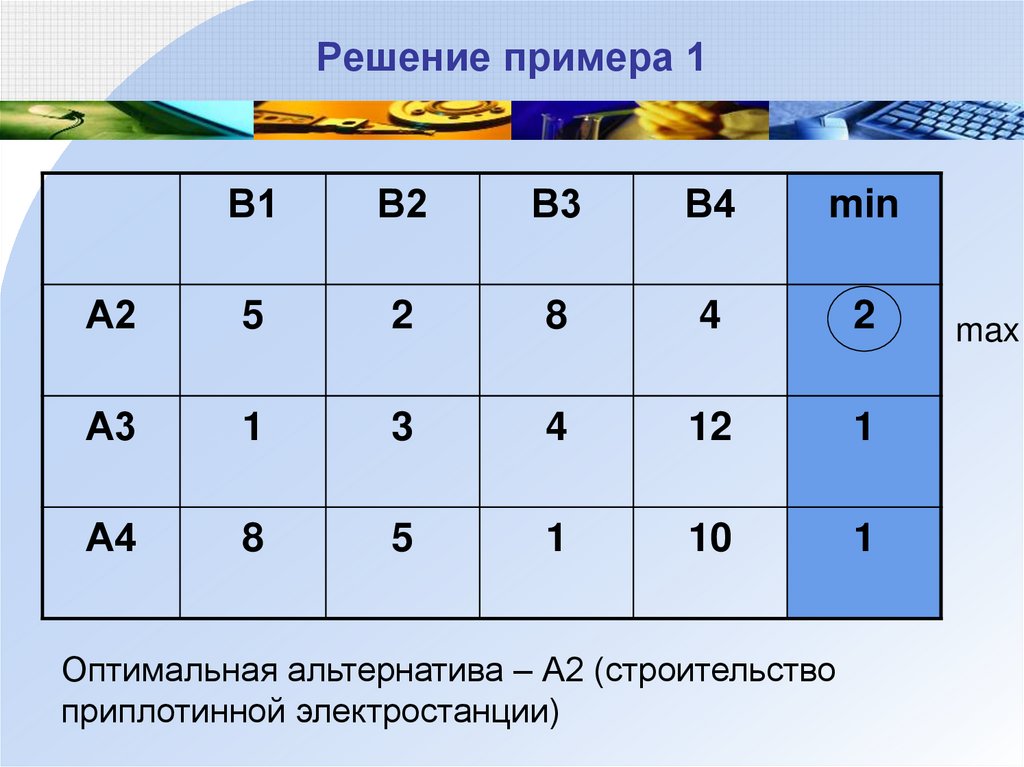
16. Решение примера 1
В1В2
В3
В4
min
А2
5
2
8
4
2
А3
1
3
4
12
1
А4
8
5
1
10
1
Оптимальная альтернатива – А2 (строительство
приплотинной электростанции)
max
17. Критерий Лапласа
Гипотеза: "Поскольку мы ничего незнаем о состояниях среды, надо считать их
равновероятными"
m
Оценка альтернативы:
1
j
W (i) ai
m j 1
Оптимальная стратегия в задаче на max:
W (i ) max W (i)
*
1 i n
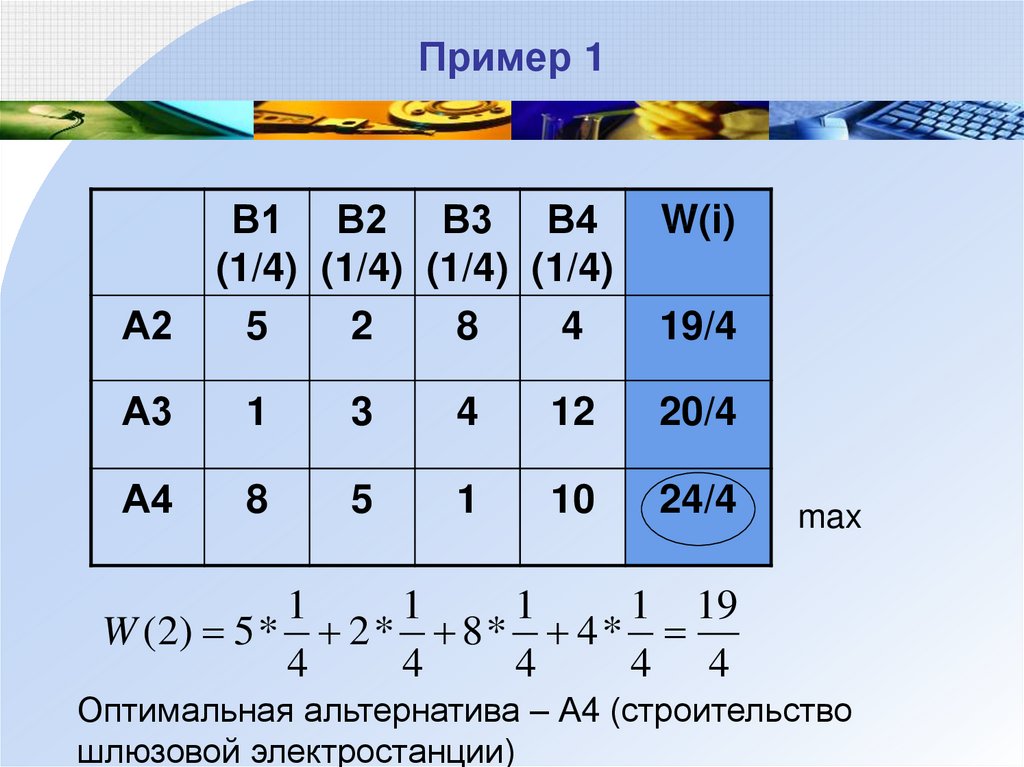
18. Пример 1
А2В1 В2 В3 В4
(1/4) (1/4) (1/4) (1/4)
5
2
8
4
W(i)
19/4
А3
1
3
4
12
20/4
А4
8
5
1
10
24/4
max
1
1
1
1 19
W (2) 5 * 2 * 8 * 4 *
4
4
4
4 4
Оптимальная альтернатива – А4 (строительство
шлюзовой электростанции)
19. Критерий Сэвиджа
Пусть целевая функция F(x,y) есть функциявыигрыша ОС. Следовательно, ОС стремится
максимизировать целевую функцию
Составим функцию сожаления для задачи на max:
( x, y ) max F ( x, y ) F ( x, y )
x
Функция сожаления для задачи на min:
( x, y ) F ( x, y ) min F ( x, y )
x
Затем для функции ( x, y ) применяется критерий
наилучшего гарантированного результата, то есть
W ( x*) min max ( x, y)
x
y
20. Пример 1
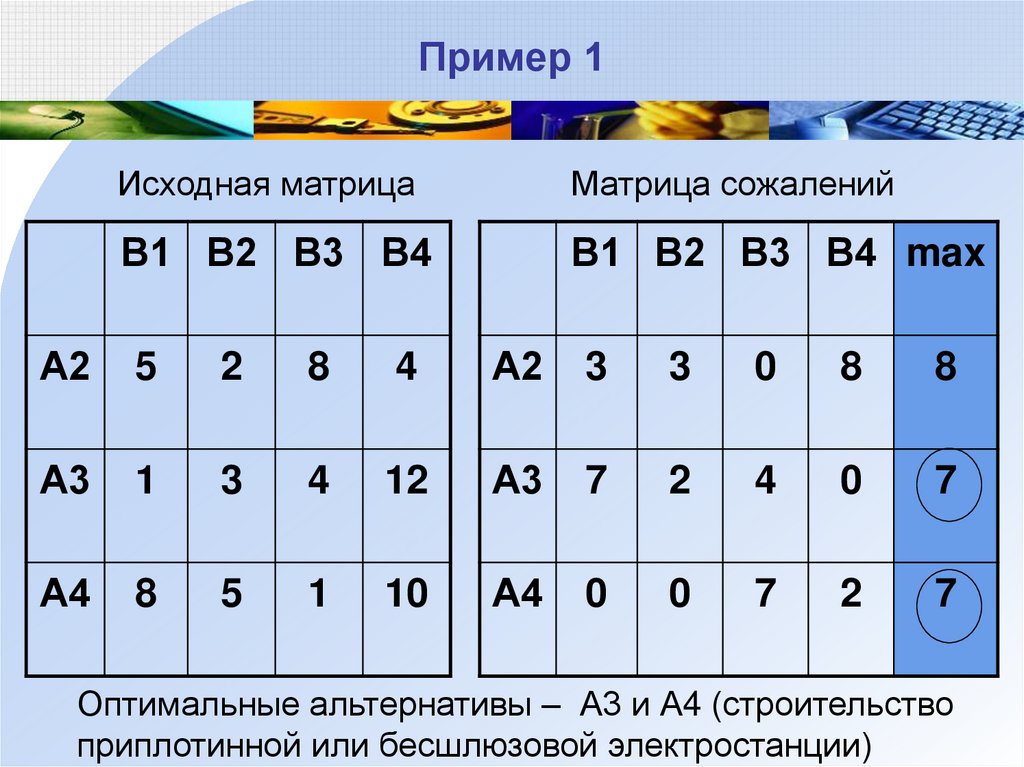
Исходная матрицаМатрица сожалений
В1 В2 В3 В4
В1 В2 В3 В4 max
А2
5
2
8
4
А2
3
3
0
8
8
А3
1
3
4
12
А3
7
2
4
0
7
А4
8
5
1
10
А4
0
0
7
2
7
Оптимальные альтернативы – А3 и А4 (строительство
приплотинной или бесшлюзовой электростанции)
21. Критерий Гурвица
ГИПОТЕЗА: при выборе альтернативы необходиморуководствоваться средним результатом,
характеризующем состояние между
крайним пессимизмом и безудержным
оптимизмом
0 1
Оценка альтернативы
для задачи на max:
W (i) min aij (1 ) max aij
j
j
Оценка альтернативы W (i ) max aij (1 ) min aij
j
j
для задачи на min:
22. Критерий Гурвица
Оптимальная стратегия в задаче на max:W (i ) max W (i)
*
1 i n
Оптимальная стратегия в задаче на min:
W (i ) min W (i)
*
1 i n
23. Пример 1
В1В2
В3
В4
А2
5
2
8
4
8
2
6
А3
1
3
4
12
12
1
8,3
А4
8
5
1
10
10
1
7
max min W(i)
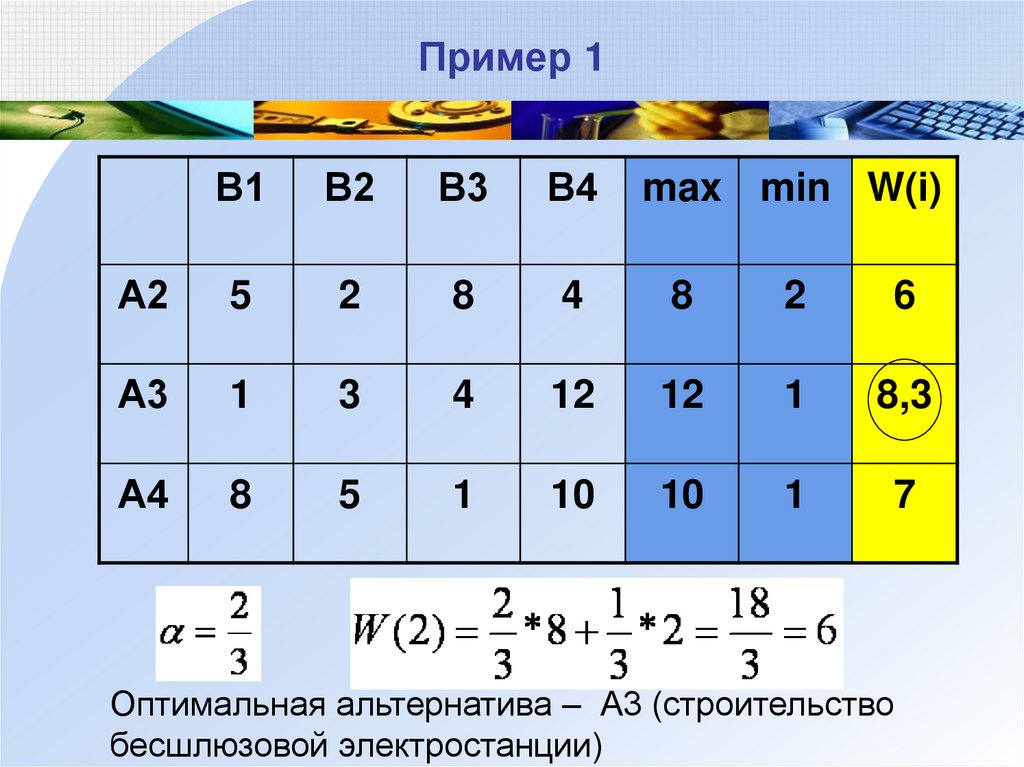
Оптимальная альтернатива – А3 (строительство
бесшлюзовой электростанции)
24. Выводы
Критерий Вальда – альтернатива 2Критерий Лапласа – альтернатива 4
Критерий Сэвиджа – альтернативы 3 и 4
Критерий Гурвица – альтернатива 3
25. Принятие решений в условиях риска
LOGO26. Типы критериев
Ожидаемое значениеn
W (i) aij * Pj , i 1, m
j 1
Ожидаемые упущенные возможности
n
W (i) rij * Pj , i 1, m
j 1
Ожидаемое значение - Риск
W (i ) M ( x) D( x)
D( x) M ( x ) ( M ( x))
2
2
27. Пример. Ожидаемое значение
Pi 0,2 0,3 0,4 0,1В1 В2 В3 В4
А2
А3
А4
5
1
8
2
3
5
8
4
1
4
12
10
W ( А2 ) 0,2 * 5 0,3 * 2 0,4 * 8 0,1* 4 5,2
W ( A3 ) 3,9
W ( A4 ) 4,5
28. Пример. Ожидаемые упущенные возможности
Pj 0,2 0,3 0,4 0,1В1 В2 В3 В4
А2
А3
А4
3
7
0
3
2
0
0
4
7
8
0
2
W ( А2 ) 0,2 * 3 0,3 * 3 0,4 * 0 0,1* 8 2,3
W ( A3 ) 3,6
W ( A4 ) 3,0
29. Пример. Ожидаемое значение - риск
Pi 0,2 0,3 0,4 0,1В1 В2 В3 В4
А2
А3
А4
5
1
8
2
3
5
8
4
1
4
12
10
W ( А2 ) M ( A2 ) D( A2 ) 5,2 6,36 2,67
M ( A2 ) 5,2
D( A2 ) (5,2 5) 2 * 0,2 (5,2 2) 2 * 0,3 (5,2 8) 2 * 0,4 (5,2 4) 2 * 0,1 6,36























 management
management








