Similar presentations:
Готовимся к ЕГЭ. Площади поверхности геометрических тел
1. Готовимся к ЕГЭ. Площади поверхности геометрических тел
Урок 942.
Краткие теоретические сведения.Цилиндром называется фигура, полученная при вращении
прямоугольника вокруг оси, содержащей его сторону.
Sбок 2 rh
Sполн 2 r 2 2 rh
V Sоснh r 2 h
03.04.2023
2
3.
Краткие теоретические сведения.Конусом называется фигура, полученная при вращении
прямоугольного треугольника вокруг оси, содержащей его катет.
Sбок rl
Sполн r 2 rl
1
1 2
V Sоснh r h
3
3
03.04.2023
3
4.
Краткие теоретические сведения.Конусом называется фигура, полученная при вращении
прямоугольного треугольника вокруг оси, содержащей его катет.
S 4 R 2
R
V
03.04.2023
4 3
R
3
4
5.
Краткие теоретические сведения.Площади подобных фигур относятся
как коэффициент подобия в квадрате.
Объемы подобных фигур относятся
как коэффициент подобия в кубе.
03.04.2023
5
6.
Цилиндр03.04.2023
6
7.
Площадь боковой поверхности цилиндра равна 2П , а диаметроснования – 1. Найдите высоту цилиндра.
№1
Решение:
Sбок 2 Rh
Sбок
h
2 Rh
h
R
Для того чтобы воспользоваться данной
формулой, нам необходимо найти радиус :
d 1
R 0 ,5
2 2
2
h
2
2 0 ,5
Ответ: 2
Талалайкин Александр 11 «В»
8.
Длина окружности основания цилиндра равна 3, высота2.Найдите площадь боковой поверхности цилиндра.
№2
Решение:
Sбок 2 rh
2
2 r - длина окружности основания
Sбок 3 2 6
Ответ: 6
Дячук Дмитрий 11 «В»
8
9. Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен ,
Найдите площадь боковой поверхности правильнойтреугольной призмы, описанной около цилиндра, радиус
основания которого равен 3 , а высота равна 2.
B1
О1
А1
Sбок Pосн H
Решение:
С1
№3
ABC-правильный (AB= a3)
B
Оr
2
А
B
О
А
r
С
С
a3
r
2 3
a3 r 2 3
a3 2 3 3 6
Pосн a3 3 18
Sбок 18 2 36
Ответ: 3
6
Авдеев Александр 11 «В»
10.
Конус03.04.2023
10
11.
Во сколько раз увеличится площадь боковой поверхностиконуса, если его образующая увеличится в 3 раза, а радиус
основания останется прежним?
№4
Решение:
Sбок 1 rl
3l
Sбок 2 r 3l
l
r
r
Составим отношение:
Sбок 1
rl
1
Sбок 2
r 3 l
3
Ответ: 3
в три раза
12.
Площадь полной поверхности конуса равна 12. Параллельнооснованию конуса проведено сечение, делящее высоту
пополам. Найдите площадь полной поверхности отсеченного
конуса.
№5
Решение:
k
Конусы подобны
Sм
1
Sб
2
Sм
1
12
4
Ответ: 3
Sм
1
2
2
12 1
3
4
13.
Сфера. Шар.03.04.2023
13
14.
Площадь большого круга шара равна 3. Найдите площадьповерхности шара.
№6
Решение:
R
R
Sкр
Sш 4
Sкр
Sкр R2
Sш 4 R
2
2
4
Ответ: 1 2
3
12
15.
Во сколько раз увеличится площадь поверхности шара, еслирадиус шара увеличить в 2 раза?
№7
Решение:
k
Шары подобны
Sм
1
Sб
2
1
2
2
Sм
1
в четыре раза
Sб
4
Ответ: 4
16. Около шара описан цилиндр, площадь поверхности которого равна 18. Найдите площадь поверхности шара
№8Решение:
Е1
А
По построению радиусы шара и
основания цилиндра равны. Площадь
поверхности цилиндра, с радиусом
основания R и высотой 2R равна
Sц 2 Sосо Sбок 2 R 2 2 Rh
2 R 2 2 R 2 R 6 R 2
Sш 4 r 2
03.04.2023
6 R 2 18
Составим отношение:
2
4 R
Sш
18 4
Sш
12
6
Ответ:
1 2
16
Булгаков Ильяс 11«А»
17. Радиусы двух шаров равны 7 и 24. Найдите радиус шара, площадь поверхности которого равна сумме площадей их поверхностей.
№9Решение:
S1 4 7 2
7
24
S2 4 24 2
S1 S2 4 ( 7 2 24 2 ) Sб
Sб 4 Rб 4 ( 7 2 24 2 )
2
R 7 2 24 2 625
Ответ: 2
03.04.2023
R 25
5
17
Булгаков Ильяс 11«А»
18.
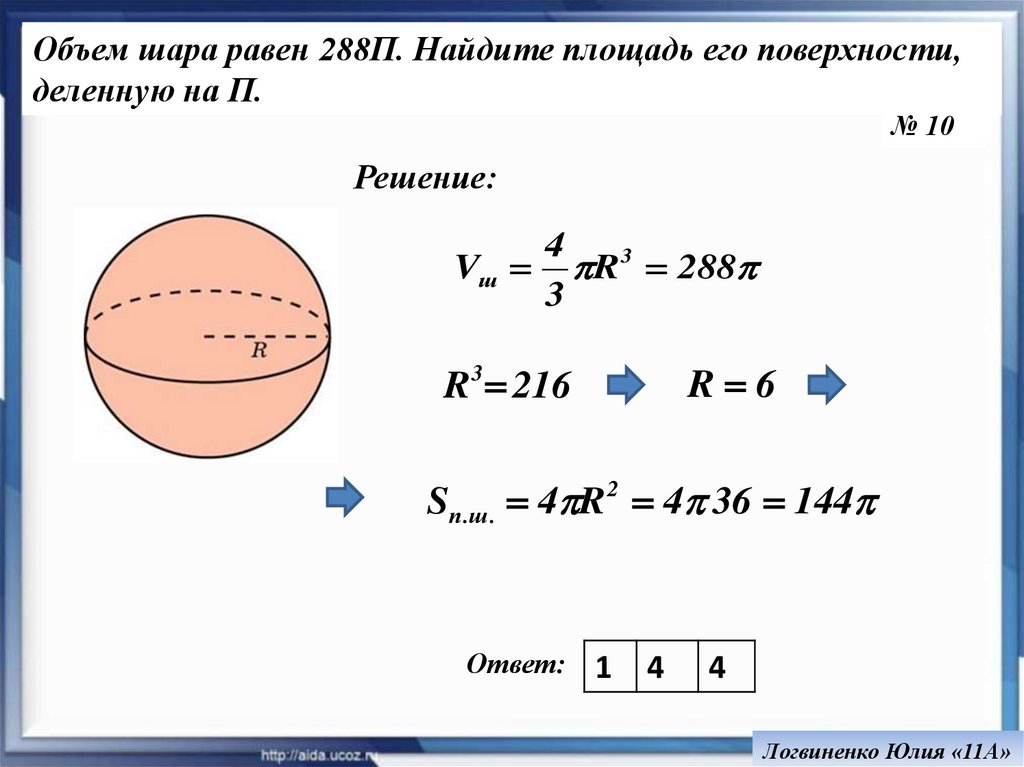
Объем шара равен 288П. Найдите площадь его поверхности,деленную на П.
№ 10
Решение:
4
Vш R 3 288
3
R 6
R 3 216
Sп .ш . 4 R 2 4 36 144
Ответ:
1
4
4
Логвиненко Юлия «11А»
19. Объем одного шара в 27 раз больше объема второго. Во сколько раз площадь поверхности первого шара больше площади поверхности
второго?№ 11
Решение:
V2
1
Все шары подобны
V1 27
V2
V1
Объемы подобных фигур
относятся как k 3
(коэффициент подобия)
Площади подобных фигур
относятся как k 2
(коэффициент подобия)
1
k
3
S2
1
2
k
S1
9
Ответ: 9
03.04.2023
19
Карагяур Лилия «11 А»
20. Домашнее задание
• 1. Шар вписан в цилиндр. Площадь полнойповерхности цилиндра равна 18. Найдите
площадь поверхности шара.
03.04.2023
20
21. Домашнее задание
• 2. Из единичного куба вырезанаправильная четырехугольная призма со
стороной основания 0,5 и боковым ребром
1. Найдите площадь поверхности
оставшейся части куба.
03.04.2023
21
22. Домашнее задание
• 3. равильная четырехугольная призмаописана около цилиндра, радиус основания
которого равен 2. Площадь боковой
поверхности призмы равна 48. Найдите
высоту цилиндра.
03.04.2023
22
23. Домашнее задание
• 4. Шар вписан в цилиндр. Площадьповерхности шара равна 111. Найдите
площадь полной поверхности цилиндра.
03.04.2023
23
24. Домашнее задание
03.04.202324























 mathematics
mathematics








